In this document we discuss the finite-element-based solution of the Helmholtz equation in cylindrical polar coordinates, using a Fourier-decomposition of the solution in the azimuthal direction. This is useful for solving time-harmonic wave problems in 3D axisymmetric domains, e.g. the scattering of acoustic sound field from a sphere, the example we consider below.

Acknowledgement: This implementation of the equations and the documentation were developed jointly with Ahmed Wassfi (EnstaParisTech, Paris).

Theory: The Fourier-decomposed Helmholtz equation

The Helmholtz equation governs time-harmonic solutions of problems governed by the linear wave equation

$\nabla^2 U(x,y,z,t) = \frac{1}{c^2} \frac{\partial^2 U(x,y,z,t)}{\partial t^2}, \ \ \ \ \ \ \ \ \ \ \ \ (1)$

where is the wavespeed. Assuming that is time-harmonic, with frequency $\omega$ , we write the real function as

$U(x,y,z,t) = Re ({\tt U}(x,y,z) \ e^{-i \omega t}) \ \ \ \ \ \ \ \ \ \ \ \ (2)$

where ${\tt U}(x,y,z)$ is complex-valued. This transforms (1) into the Helmholtz equation

$\nabla^2 {\tt U}(x,y,z) + k^2 {\tt U} = 0 \ \ \ \ \ \ \ \ \ \ \ \ (3)$

where

$k = \frac{\omega}{c} \ \ \ \ \ \ \ \ \ \ \ \ (4)$

is the wave number. Like other elliptic PDEs the Helmholtz equation admits Dirichlet, Neumann (flux) and Robin boundary conditions.

If the equation is solved in an infinite domain (e.g. in scattering problems) the solution must satisfy the so-called Sommerfeld radiation condition which in 3D has the form

$\lim_{r\to \infty} r \left(\frac{\partial {\tt U}}{\partial r} - ik{\tt U} \right) =0.$

Mathematically, this conditions is required to ensure the uniqueness of the solution (and hence the well-posedness of the problem). In a physical context, such as a scattering problem, the condition ensures that scattering of an incoming wave only produces outgoing not incoming waves from infinity.

These equations can be solved using oomph-lib's cartesian Helmholtz elements, described in
another tutorial. Here we consider an alternative approach in which we solve the equations in cylindrical polar coordinates $(r,\varphi,z)$ , related to the cartesian coordinates via

$x = r \cos(\varphi),$

$y = r \sin(\varphi),$

$z = z.$

We then decompose the solution into its Fourier components by writing

${\tt U}(r,\varphi,z) = \sum_{N=-\infty}^{\infty} u_N(r,z) \exp({\rm i} N \varphi).$

Since the governing equations are linear we can compute each Fourier component individually by solving

$\nabla^2 {u_{N}}(r,z) + \left(k^2-\frac{N^2}{r^2}\right) u_N(r,z) = 0 \ \ \ \ \ \ \ \ \ \ \ \ (5)$

while specifying the Fourier wavenumber as a parameter.

Discretisation by finite elements

The discretisation of the Fourier-decomposed Helmholtz equation itself only requires a trivial modification of its cartesian counterpart. Since most practical applications of the Helmholtz equation involve complex-valued solutions, we provide separate storage for the real and imaginary parts of the solution – each Node therefore stores two unknowns values. By default, the real and imaginary parts are stored as values 0 and 1, respectively; see the section The enumeration of the unknowns for details.

The application of Dirichlet and Neumann boundary conditions is straightforward and follows the pattern employed for the solution of the Poisson equation:

Dirichlet conditions are imposed by pinning the relevant nodal values and setting them to the appropriate prescribed values.
Neumann (flux) boundary conditions are imposed via FaceElements (here the FourierDecomposedHelmholtzFluxElements). As usual we attach these to the faces of the "bulk" elements that are subject to the Neumann boundary conditions.

The imposition of the Sommerfeld radiation condition for problems in infinite domains is slightly more complicated. In the following discussion we will assume that the infinite domain is truncated at a spherical artificial boundary $\Gamma$ of radius [The methodology can easily be modified to deal with other geometries but this has not been done yet – any volunteers?]. All methods exploit the fact that the relevant solution of the Helmholtz equation can be written in spherical polar coordinates $(\rho,\varphi,\theta)$ as

${\tt U}(\rho,\theta,\varphi)= \sum_{l=0}^{+\infty}\sum_{n=-l}^{l} \left( a_{ln} \ h_{l}^{(1)}(k\rho)+ b_{ln} \ h_{l}^{(2)}(k\rho) \right)P_{l}^{n} (\cos\theta)\exp({\rm i} n \varphi). \ \ \ \ \ \ \ (6)$

where the $a_{ln}, b_{ln}$ are arbitrary coefficients and the functions

$h_{l}^{(1)}(x)=j_{l}(x)+{\rm i} y_{l}(x) \mbox{ \ \ \ \ and \ \ \ \ } h_{l}^{(2)}(x)=j_{l}(x)-{\rm i} y_{l}(x)$

are the spherical Hankel functions of first and second kind, respectively, expressed in terms the spherical Bessel functions

$j_{l}(x)=\sqrt{\frac{\pi}{2x}}J_{l+1/2}(x) \mbox{ \ \ \ \ and \ \ \ \ } y_{l}(x)=\sqrt{\frac{\pi}{2x}}Y_{l+1/2}(x).$

The functions

$P_{l}^{m}(x)=(-1)^{m}(1-x^2)^{m/2}\frac{d^m}{dx^m}P_{l}(x)$

are the associated Legendre functions, expressed in terms of the Legendre polynomials

$P_{n}(x)=\frac{1}{2^{n} \, n!}\frac{d^n}{dx^n}[(x^2-1)^{n}].$

This definition shows that $P_{l}^{m}(x)=0$ for which explains the limited range of summation indices in the second sum in (6).

The relation between the cylindrical polar coordinates $(r,\varphi,z)$ and spherical polar coordinates $(\rho,\theta,\varphi)$ is given by

$\rho = \sqrt{r^2 + z^2},$

$\theta = \arctan(r/z),$

$\varphi = \varphi,$

so $\varphi \in [0,2\pi]$ remains unchanged, and
$\theta \in [0,\pi]$ sweeps from the north pole ( $\theta = 0$ ), via the equator ( $\theta = \pi/2$ ) to the south pole ( $\theta = \pi$ ).

The Dirichlet-to-Neumann mapping (DtN)

Assuming that the artificial outer boundary $\Gamma$ is sufficiently far from the region of interest, so that any near field effects associated with the scatterer have decayed, we have to ensure that the solution on $\Gamma$ contains only outgoing waves. For our choice of the time-dependence in (2), such waves are represented by the terms involving the spherical Hankel functions of the first kind, $h_l^{(1)}$ , in (6).

The solution on (and near) $\Gamma$ is therefore given by

${\tt U}(\rho,\theta,\phi)= \sum_{l=0}^{+\infty}\sum_{n=-l}^{l} \ a_{ln}\ h_{l}^{(1)}(k\rho) \ P_{l}^{n}(\cos\theta) \ \exp({\rm i}n\varphi).$

Restricting ourselves to the single azimuthal Fourier mode to be determined by (5), we have

$u_N(\rho,\theta)=\sum_{l=N}^{+\infty} a_{l} \ h_{l}^{(1)}(k\rho)\ P_{l}^{N}(\cos\theta). \ \ \ \ \ \ \ (7)$

We multiply this equation by $P_{n}^{N}(\cos\theta) \sin(\theta)$ , integrate over $\theta$ , and exploit the orthogonality of the Legendre functions, to show that

$a_{l}=\frac{2l+1}{2 h_{l}^{(1)}(kR)} \frac{(l-N)!}{(l+N)!}\int_{0}^{\pi} u(R,\theta)\ P_{l}^{N}(\cos\theta) \ \sin(\theta) \ d\theta.$

Using these coefficients, we can differentiate (7) to obtain the normal derivative of the solution on the (spherical) artificial outer boundary $\Gamma$ in terms of the solution itself:

$\left. \frac{\partial u}{\partial n} \right|_{\rho=R} = \left. \frac{\partial u}{\partial \rho} \right|_{\rho=R} = \gamma(u) = k\sum_{n=N}^{\infty}a_{n} \ h_{n}^{(1)'}(kR)\ P_{n}^{N}(\cos \theta)$

i.e.

$\gamma(u(R,\theta))= k \sum_{n=N}^{\infty} h_{n}^{(1)'}(kR) \ P_{n}^{N}(\cos \theta) \ \frac{2n+1}{2h_{n}^{(1)}(kR)}\frac{(n-N)!}{(n+N)!} \int_{0}^{\pi} u(R,\overline{\theta}) \ P_{n}^{N}(\cos\overline{\theta}) \ \sin(\overline{\theta}) \; d\overline{\theta}, \ \ \ \ \ \ \ \ \ \ (8)$

a Dirichlet-to-Neumann mapping.

Equation (8) provides a condition on the normal derivative of the solution along the artificial boundary and is implemented in the FourierDecomposedHelmholtzDtNBoundaryElement class. Since $\gamma$ depends on the solution everywhere along the artificial boundary, the application of the Sommerfeld radiation condition via (8) introduces a non-local coupling between all the degrees of freedom located on that boundary. This is handled by classifying the unknowns that affect $\gamma$ but are not associated with an element's own nodes as its external Data.

To facilitate the setup of the interaction between the FourierDecomposedHelmholtzDtNBoundaryElements, oomph-lib provides the class FourierDecomposedHelmholtzDtNMesh which provides storage for (the pointers to) the FourierDecomposedHelmholtzDtNBoundaryElements that discretise the artificial boundary. The member function FourierDecomposedHelmholtzDtNMesh::setup_gamma() pre-computes the $\gamma$ values required for the imposition of equation (8). The radius of the artificial boundary and the (finite) upper limit for the sum in (8) are specified as arguments to the constructor of the FourierDecomposedHelmholtzDtNMesh.

NOTE: Since $\gamma$ depends on the solution, it must be recomputed whenever the unknowns are updated during the Newton iteration. This is best done by adding a call to FourierDecomposedHelmholtzDtNMesh::setup_gamma() to Problem::actions_before_newton_convergence_check(). [If Helmholtz's equation is solved in isolation (or within a coupled, but linear problem), Newton's method will converge in one iteration. In such cases the unnecessary recomputation of $\gamma$ after the one-and-only Newton iteration can be suppressed by setting Problem::Problem_is_nonlinear to false.]

A specific example

We will now demonstrate the methodology for a specific example for which the exact solution of (5) is given by

$u_N(r,z)=u_N^{[exact]}(r,z)=\sum_{l=N}^{N_{\rm terms}} h_{l}^{(1)}(k\sqrt{r^2+z^2}) \ P_{l}^{N}\left(\frac{z}{\sqrt{r^2+z^2}}\right).$

This solution corresponds to the superposition of several outgoing waves of the form (7) with coefficients . We solve the Helmholtz equation in the infinite region surrounding the unit sphere on whose surface we impose flux boundary conditions consistent with the derivative of the exact solution.

To solve this problem numerically, we discretise the annular domain $1 < \sqrt{r^2 + z^2} < 3$ with finite elements and apply the Sommerfeld radiation condition using a Dirichlet-to-Neumann mapping on the artificial outer boundary $\Gamma$ located at $\sqrt{r^2 + z^2} = R = 3$ .

The two plots below show a comparison between the exact and computed solutions for $N_{\rm terms}=6$ , a Fourier wavenumber of , and a (squared) Helmholtz wavenumber of .

Plot of the exact (green) and computed (red) real parts of the solution of the Fourier-decomposed Helmholtz equation for N=3 and a wavenumber of k^2 = 10.

Plot of the exact (green) and computed (red) imaginary parts of the solution of the Fourier-decomposed Helmholtz equation for N=3 and a wavenumber of k^2 = 10.

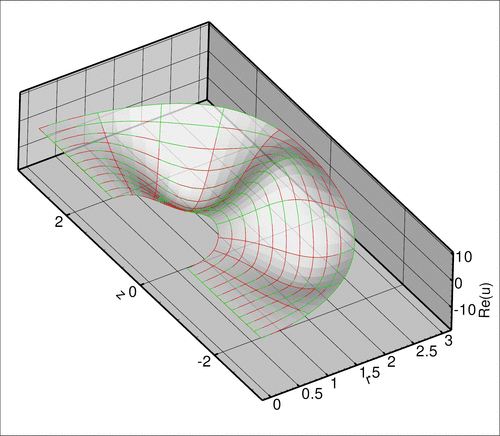
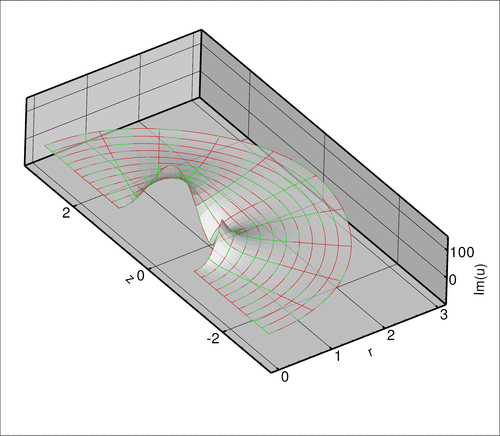
The numerical solution

The global namespace

As usual, we define the problem parameters in a global namespace. The main parameter are the (square of the) Helmholtz wave number, , and the Fourier wavenumber, . The parameter Nterms_for_DtN determines how many terms are to be used in the computation of the $\gamma$ integral in the Dirichlet-to-Neumann mapping (8); see The accuracy of the boundary condition elements.

//===== start_of_namespace=============================================
/// Namespace for the Fourier decomposed Helmholtz problem parameters
//=====================================================================
namespace ProblemParameters
{
 /// Square of the wavenumber
 double K_squared=10.0;
 
 /// Fourier wave number
 int N_fourier=3;
 
 /// Number of terms in computation of DtN boundary condition
 unsigned Nterms_for_DtN=6;

Next we define the coefficients

 
 /// Number of terms in the exact solution
 unsigned N_terms=6; 
 
 /// Coefficients in the exact solution
 Vector<double> Coeff(N_terms,1.0);
 
 /// Imaginary unit 
 std::complex<double> I(0.0,1.0); 

required for the specification of the exact solution

/// Exact solution as a Vector of size 2, containing real and imag parts

void get_exact_u(const Vector<double>& x, Vector<double>& u)

ProblemParameters::get_exact_u

void get_exact_u(const Vector< double > &x, Vector< double > &u)

Exact solution as a Vector of size 2, containing real and imag parts.

Definition: sphere_scattering.cc:243

and its derivative,

 /// Get -du/dr (spherical r) for exact solution. Equal to prescribed
 /// flux on inner boundary.
 void exact_minus_dudr(const Vector<double>& x, std::complex<double>& flux)

whose listings we omit here.

The driver code

The driver code is very straightforward. We create the problem object, discretising the domain with 3x3-noded QFourierDecomposedHelmholtzElements and set up the output directory.

//===== start_of_main=====================================================
/// Driver code for Fourier decomposed Helmholtz problem
//========================================================================
int main(int argc, char **argv)
{
 // Create the problem with 2D nine-node elements from the
 // QFourierDecomposedHelmholtzElement family. 
 FourierDecomposedHelmholtzProblem<QFourierDecomposedHelmholtzElement<3> > 
  problem;
 
 // Create label for output
 DocInfo doc_info;
 
 // Set output directory
 doc_info.set_directory("RESLT");

We solve the problem for a range of Fourier wavenumbers and document the results.

 
 // Solve for a few Fourier wavenumbers
 for (ProblemParameters::N_fourier=0;ProblemParameters::N_fourier<4;
      ProblemParameters::N_fourier++)
  {
   // Step number
   doc_info.number()=ProblemParameters::N_fourier;
   
   // Solve the problem
   problem.newton_solve();
   
   //Output the solution
   problem.doc_solution(doc_info);
  }
 
} //end of main

The problem class

The problem class is very similar to that employed for the solution of the 2D Poisson equation with flux boundary conditions or, of course, the 2D cartesian Helmholtz problem discussed in another tutorial.

We provide two separate meshes of FaceElements: one for the inner boundary where the FourierDecomposedHelmholtzFluxElements apply the Neumann condition, and one for the outer boundary where we apply the (approximate) Sommerfeld radiation condition. As discussed in section The Dirichlet-to-Neumann mapping (DtN) , we use the function actions_before_newton_convergence_check() to recompute the $\gamma$ integral whenever the unknowns are updated during the Newton iteration.

//========= start_of_problem_class=====================================
/// Problem class 
//=====================================================================
template<class ELEMENT> 
class FourierDecomposedHelmholtzProblem : public Problem
{
 
public:
 
 /// Constructor
 FourierDecomposedHelmholtzProblem();
 
 /// Destructor (empty)
 ~FourierDecomposedHelmholtzProblem(){}
 
 /// Update the problem specs before solve (empty)
 void actions_before_newton_solve(){}
 
 /// Update the problem after solve (empty)
 void actions_after_newton_solve(){}
 
 /// Doc the solution. DocInfo object stores flags/labels for where the
 /// output gets written to
 void doc_solution(DocInfo& doc_info);
  
 /// Recompute gamma integral before checking Newton residuals
 void actions_before_newton_convergence_check()
  {
   Helmholtz_outer_boundary_mesh_pt->setup_gamma();
  }
 
 /// Check gamma computation
 void check_gamma(DocInfo& doc_info);
  
private:
 
 /// Create BC elements on outer boundary
 void create_outer_bc_elements();
 
 /// Create flux elements on inner boundary
 void create_flux_elements_on_inner_boundary();
 
 /// Pointer to bulk mesh
 AnnularQuadMesh<ELEMENT>* Bulk_mesh_pt;
  
 /// Pointer to mesh containing the DtN boundary
 /// condition elements
 FourierDecomposedHelmholtzDtNMesh<ELEMENT>* Helmholtz_outer_boundary_mesh_pt;
 
 /// Mesh of face elements that apply the prescribed flux
 /// on the inner boundary
 Mesh* Helmholtz_inner_boundary_mesh_pt;
 
}; // end of problem class

The problem constructor

We start by building the bulk mesh, using the TwoDAnnularMesh.

//=======start_of_constructor=============================================
/// Constructor for Fourier-decomposed Helmholtz problem
//========================================================================
template<class ELEMENT>
FourierDecomposedHelmholtzProblem<ELEMENT>::
FourierDecomposedHelmholtzProblem()
{ 
 
// Build annular mesh
  
// # of elements in r-direction 
 unsigned n_r=10*ProblemParameters::El_multiplier;
 
 // # of elements in theta-direction 
 unsigned n_theta=10*ProblemParameters::El_multiplier;
 
 // Domain boundaries in theta-direction
 double theta_min=-90.0;
 double theta_max=90.0;
 
 // Domain boundaries in r-direction
 double r_min=1.0;
 double r_max=3.0;
 
 // Build and assign mesh
 Bulk_mesh_pt = 
  new AnnularQuadMesh<ELEMENT>(n_r,n_theta,r_min,r_max,theta_min,theta_max);

Next we create and populate the mesh of elements containing the DtN boundary elements on the artificial outer boundary,

 
 // Create mesh for DtN elements on outer boundary
 Helmholtz_outer_boundary_mesh_pt=
  new FourierDecomposedHelmholtzDtNMesh<ELEMENT>(
   r_max,ProblemParameters::Nterms_for_DtN);
 
 // Populate it with elements
 create_outer_bc_elements();

and attach flux elements to the inner boundary:

 
 // Create flux elements on inner boundary
 Helmholtz_inner_boundary_mesh_pt=new Mesh;
 create_flux_elements_on_inner_boundary();

We combine the various meshes to a global mesh,

 
 // Add the several  sub meshes to the problem
 add_sub_mesh(Bulk_mesh_pt); 
 add_sub_mesh(Helmholtz_inner_boundary_mesh_pt); 
 add_sub_mesh(Helmholtz_outer_boundary_mesh_pt); 
  
 // Build the Problem's global mesh from its various sub-meshes
 build_global_mesh();

pass the problem parameters to the bulk elements,

 
 // Complete the build of all elements so they are fully functional
 unsigned n_element = Bulk_mesh_pt->nelement();
 for(unsigned i=0;i<n_element;i++)
  {
   // Upcast from GeneralsedElement to the present element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(Bulk_mesh_pt->element_pt(i));
   
   //Set the k_squared pointer
   el_pt->k_squared_pt()=&ProblemParameters::K_squared;
   
   // Set pointer to Fourier wave number
   el_pt->fourier_wavenumber_pt()=&ProblemParameters::N_fourier;
  }

and set up the equation numbering scheme:

 
 // Setup equation numbering scheme
 cout <<"Number of equations: " << assign_eqn_numbers() << std::endl; 
 
} // end of constructor

The problem is now ready to be solved.

Creating the face elements

The functions create_flux_elements(...) and create_outer_bc_elements(...) create the FaceElements required to apply the boundary conditions on the inner and outer boundaries of the annular computational domain. They both loop over the bulk elements that are adjacent to the appropriate mesh boundary and attach the required FaceElements to their faces. The newly created FaceElements are then added to the appropriate mesh.

//============start_of_create_outer_bc_elements==============================
/// Create BC elements on outer boundary
//========================================================================
template<class ELEMENT>
void FourierDecomposedHelmholtzProblem<ELEMENT>::create_outer_bc_elements()
{
 // Outer boundary is boundary 1:
 unsigned b=1;
 
 // Loop over the bulk elements adjacent to boundary b?
 unsigned n_element = Bulk_mesh_pt->nboundary_element(b);
 for(unsigned e=0;e<n_element;e++)
  {
   // Get pointer to the bulk element that is adjacent to boundary b
   ELEMENT* bulk_elem_pt = dynamic_cast<ELEMENT*>(
    Bulk_mesh_pt->boundary_element_pt(b,e));
   
   //Find the index of the face of element e along boundary b 
   int face_index = Bulk_mesh_pt->face_index_at_boundary(b,e);
   
   // Build the corresponding DtN element
   FourierDecomposedHelmholtzDtNBoundaryElement<ELEMENT>* flux_element_pt = new 
    FourierDecomposedHelmholtzDtNBoundaryElement<ELEMENT>(bulk_elem_pt,
                                                          face_index);
   
   //Add the flux boundary element to the  helmholtz_outer_boundary_mesh
   Helmholtz_outer_boundary_mesh_pt->add_element_pt(flux_element_pt);
 
   // Set pointer to the mesh that contains all the boundary condition
   // elements on this boundary
   flux_element_pt->
    set_outer_boundary_mesh_pt(Helmholtz_outer_boundary_mesh_pt);
  }
 
} // end of create_outer_bc_elements

(We omit the listing of the function create_flux_elements(...) because it is very similar. Feel free to inspect in the source code.)

Post-processing

The post-processing function doc_solution(...) plots the computed and exact solutions (real and complex parts) and assesses the error in the computed solution.

//===============start_of_doc=============================================
/// Doc the solution: doc_info contains labels/output directory etc.
//========================================================================
template<class ELEMENT>
void FourierDecomposedHelmholtzProblem<ELEMENT>::doc_solution(DocInfo& doc_info)
{ 
 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points: npts x npts
 unsigned npts=5;
  
 // Output solution 
 //-----------------
 sprintf(filename,"%s/soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Bulk_mesh_pt->output(some_file,npts);
 some_file.close();
 
 
 // Output exact solution 
 //----------------------
 sprintf(filename,"%s/exact_soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Bulk_mesh_pt->output_fct(some_file,npts,ProblemParameters::get_exact_u); 
 some_file.close();
 
 
 // Doc error and return of the square of the L2 error
 //---------------------------------------------------
 double error,norm;
 sprintf(filename,"%s/error%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Bulk_mesh_pt->compute_error(some_file,ProblemParameters::get_exact_u,
                             error,norm); 
 some_file.close();
 
 // Doc L2 error and norm of solution
 cout << "\nNorm of error   : " << sqrt(error) << std::endl; 
 cout << "Norm of solution: " << sqrt(norm) << std::endl << std::endl;

The function check_gamma(...) is used to check the computation of the $\gamma$ integral. If computed correctly, its values (pre-computed at the Gauss points of the FourierDecomposedHelmholtzFluxElement) ought to agree (well) with the derivative of the exact solution. They do; see The accuracy of the boundary condition elements.

 
 // Check gamma computation
 check_gamma(doc_info);

Finally, we output the time-averaged power radiated over the outer boundary of the domain, defined as

$\overline{\cal P }_N = \pi R^2 \int_0^\pi \left. \bigg( Im \{\frac{\partial u_N}{\partial \rho} \} Re\{u_N \} - Re \{\frac{\partial u_N}{\partial \rho} \} Im\{u_N \} \bigg)\right|_{\rho=R} \sin(\theta) \ d\theta.$

We refer to another tutorial for the derivation which shows (in the context of an acoustic fluid-structure interaction problem) why this is a sensible definition of the radiated power.

 
 
 // Compute/output the radiated power
 //----------------------------------
 sprintf(filename,"%s/power%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 sprintf(filename,"%s/total_power%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 
 // Accumulate contribution from elements
 double power=0.0;
 unsigned nn_element=Helmholtz_outer_boundary_mesh_pt->nelement(); 
 for(unsigned e=0;e<nn_element;e++)
  {
   FourierDecomposedHelmholtzBCElementBase<ELEMENT> *el_pt = 
    dynamic_cast<FourierDecomposedHelmholtzBCElementBase<ELEMENT>*>(
     Helmholtz_outer_boundary_mesh_pt->element_pt(e)); 
   power += el_pt->global_power_contribution(some_file);
  }
 some_file.close();
 
 // Output total power
 oomph_info << "Radiated power: " 
            << ProblemParameters::N_fourier << " " 
            << ProblemParameters::K_squared << " " 
            << power << std::endl;
 some_file.open(filename); 
 some_file << ProblemParameters::N_fourier << " " 
           << ProblemParameters::K_squared << " " 
           << power << std::endl;
 some_file.close();
 
} // end of doc

Comments and Exercises

The enumeration of the unknowns

As discussed in the introduction, most practically relevant solutions of the Helmholtz equation are complex valued. Since oomph-lib's solvers only deal with real (double precision) unknowns, the equations are separated into their real and imaginary parts. In the implementation of the Helmholtz elements, we store the real and imaginary parts of the solution as two separate values at each node. By default, the real and imaginary parts are accessible via Node::value(0) and Node::value(1). However, to facilitate the use of the elements in multi-physics problems we avoid accessing the unknowns directly in this manner but provide the virtual function

std::complex<unsigned> FourierDecomposedHelmholtzEquations<DIM>::u_index_fourier_decomposed_helmholtz()

which returns a complex number made of the two unsigneds that indicate which nodal value represents the real and imaginary parts of the solution. This function may be overloaded in combined multi-physics elements in which a Helmholtz element is combined (by multiple inheritance) with another element, using the strategy described in the Boussinesq convection tutorial.

The accuracy of the boundary condition elements

As discussed above, the Dirichlet-to-Neumann mapping allows an "exact" implementation of the Sommerfeld radiation condition, provided the artificial outer boundary is sufficiently far from the scatterer that any near field effects have decayed. The actual accuracy of the computational results depends on various factors:

The number of FourierDecomposedHelmholtzDtNBoundaryElement along the artificial domain boundary. Since these elements are attached to the "bulk" FourierDecomposedHelmholtzElements it is important that the bulk mesh is sufficiently fine to resolve the relevant features of the solution throughout the domain.
The number of terms included in the sum (8) – specified in the call to the constructor of the FourierDecomposedHelmholtzDtNMesh.
The accuracy of the integration scheme used to evaluate the integral in (8).

Exercises

Exploiting linearity

Confirm that the (costly) re-computation of the $\gamma$ integral in actions_before_newton_convergence_check() after the first (and only) linear solve in the Newton iteration can be avoided by declaring the problem to be linear.

The accuracy of the boundary condition elements

Explore the accuracy (and computational cost) of the application of the DtN boundary condition by varying the number of terms included in the sum (8). Specifically, confirm that an obviously wrong result is obtained if we choose ProblemParameters::Nterms_for_DtN < ProblemParameters::Nterms.
Explore the function check_gamma() and confirm that the computed value for the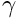 $\gamma$ integral provides a good approximation to the derivative of the exact solution. Here is a representative comparison obtained with the parameters used in the driver code listed above:

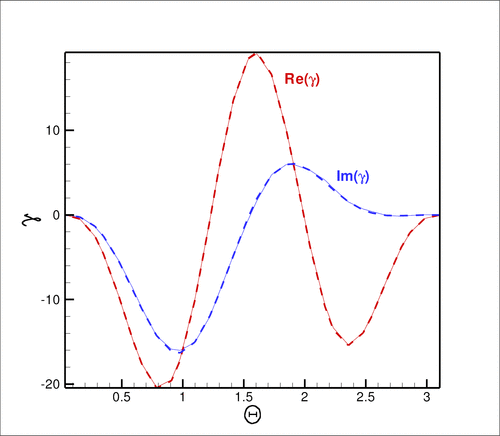
Plot of the exact (dashed) and computed (solid) gamma integral for N=3 and a wavenumber of k^2 = 10.

Scattering of a planar acoustic wave off a sound-hard sphere

Modify the driver code to compute the sound field created when a planar acoustic wave, propagating along the -axis, impinges on a sound-hard sphere. The relevant theory is described in another tutorial; you can use the fact that in spherical polar coordinates a planar wave of the form

${\tt U}(x,y,z) = \exp({\rm i}kz)$

can be written as

${\tt U}(\rho,\theta) = \sum_{l=0}^{\infty} (2l+1) \ {\rm i}^l \ j_l(kr) \ P_l(\cos\theta),$

i.e. the wave comprises a single azimuthal Fourier component with . Note that the driver code already contains a namespace PlanarWave with several (but not all!) functions required for this task.

Source files for this tutorial

The source files for this tutorial are located in the directory: demo_drivers/fourier_decomposed_helmholtz/sphere_scattering/
The driver code is: demo_drivers/fourier_decomposed_helmholtz/sphere_scattering/sphere_scattering.cc

PDF file

A pdf version of this document is available.