In this document we discuss the adaptive solution of a 2D Poisson problem with Neumann boundary conditions.

Two-dimensional model Poisson problem with Neumann boundary conditions Solve

$\sum_{i=1}^2 \frac{\partial^2u}{\partial x_i^2} = f(x_1,x_2), \ \ \ \ \ \ \ \ \ \ (1)$

in the rectangular domain $D = \left\{ (x_1,x_2) \in [0,1] \times [0,2]\right\}$ . The domain boundary $\partial D = \partial D_{Neumann} \cup \partial D_{Dirichlet}$ , where $\partial D_{Neumann} = \left\{ (x_1,x_2) | x_1=1, \ x_2\in [0,2] \right\}$ . On $\partial D_{Dirichlet}$ we apply the Dirichlet boundary conditions

$\left. u\right|_{\partial D_{Dirichlet}}=u_0, \ \ \ \ \ \ \ \ \ \ (2)$

where the function

is given. On $\partial D_{Neumann}$ we apply the Neumann conditions

$\left. \frac{\partial u}{\partial n}\right|_{\partial D_{Neumann}} = \left. \frac{\partial u}{\partial x_1}\right|_{\partial D_{Neumann}} =g_0, \ \ \ \ \ \ \ \ \ \ (3)$

where the function

is given.

In two previous examples we demonstrated two approaches for the non-adaptive solution of this problem. In both cases we created a "bulk" mesh of QPoissonElements and applied the flux boundary conditions by "attaching" PoissonFluxElements to the appropriate boundaries of the "bulk" Poisson elements. In the first implementation we simply added the pointers to the flux elements to the bulk mesh; in the second implementation we stored the surface and bulk elements in separate meshes and combined them to a single global mesh. We will now demonstrate that the second approach greatly facilitates the automatic problem adaptation. We use the mesh adaptation procedures of the RefineableQuadMesh class to adapt the bulk mesh, driven by the spatial error estimates in that mesh. The flux elements are neither involved in nor adapted by the refinement process of the bulk mesh. We therefore use the function Problem::actions_before_adapt() to delete the flux elements before the adaptation, and Problem::actions_after_adapt() to re-attach them once the bulk mesh has been adapted.

As in the previous example we choose a source function and boundary conditions for which the function

$u_0(x_1,x_2) = \tanh(1-\alpha(x_1 \tan\Phi - x_2)), \ \ \ \ \ \ \ \ \ (4)$

is the exact solution of the problem.

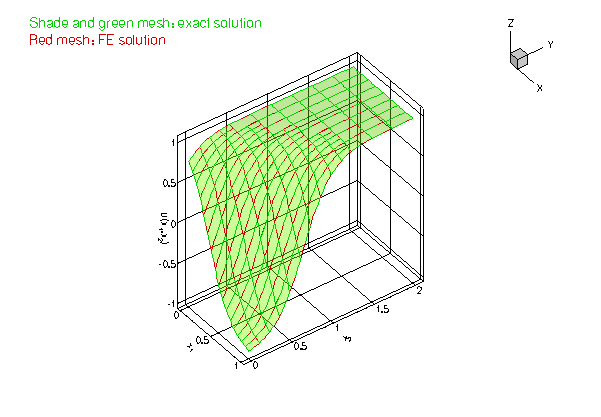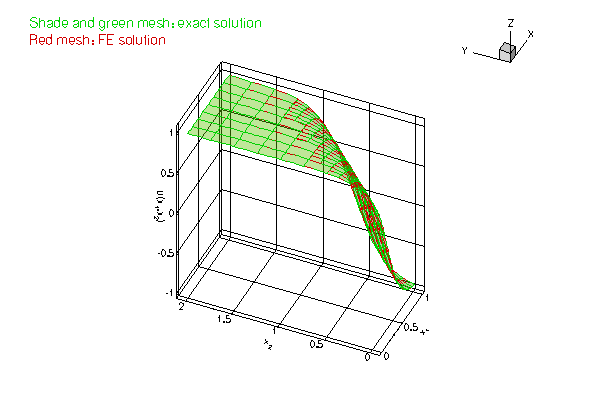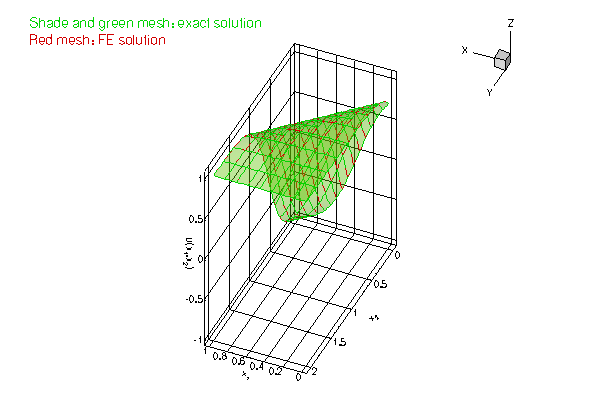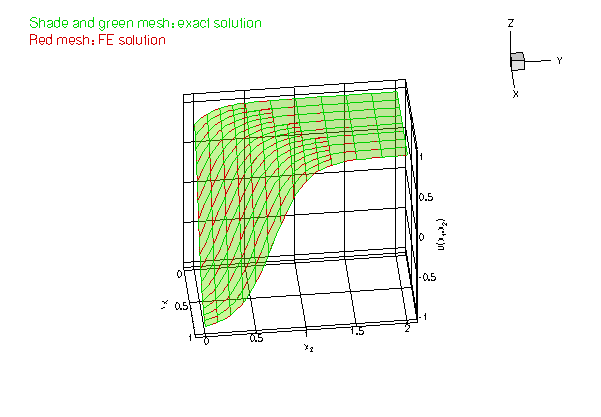
Plot of the solution obtained with automatic mesh adaptation

Since many functions in the driver code are identical to that in the non-adaptive version, discussed in the previous example, we only list those functions that differ. Please consult the source code two_d_poisson_flux_bc_adapt.cc for full details of the implementation.

Global parameters and functions

The specification of the source function and the exact solution in the namespace TanhSolnForPoisson is identical to that in the single-mesh version discussed in the previous example.

The driver code

The main code is virtually identical to that in the previous non-adaptive example . The only change is the provision of an argument to the Newton solver

// Solve the problem

problem.newton_solve(3);

which indicates that the problem should be adapted up to three times.

The problem class

The problem class is very similar to that in the non-adaptive implementation: The only difference is the provision of the functions actions_before_adapt(), actions_after_adapt(), set_prescribed_flux_pt(), and delete_flux_elements(...) which we discuss in more detail below.

//========= start_of_problem_class=====================================
/// 2D Poisson problem on rectangular domain, discretised with
/// 2D QPoisson elements. Flux boundary conditions are applied
/// along boundary 1 (the boundary where x=L). The specific type of 
/// element is specified via the template parameter.
//====================================================================
template<class ELEMENT> 
class RefineableTwoMeshFluxPoissonProblem : public Problem
{
 
public:
 
 /// Constructor: Pass pointer to source function
 RefineableTwoMeshFluxPoissonProblem(PoissonEquations<2>::PoissonSourceFctPt source_fct_pt);
 
 /// Destructor (empty)
 ~RefineableTwoMeshFluxPoissonProblem(){}
 
 /// Doc the solution. DocInfo object stores flags/labels for where the
 /// output gets written to
 void doc_solution(DocInfo& doc_info);
 
 
private:
 
 /// Update the problem specs before solve: Reset boundary conditions
 /// to the values from the exact solution.
 void actions_before_newton_solve();
 
 /// Update the problem specs after solve (empty)
 void actions_after_newton_solve(){}
 
 /// Actions before adapt: Wipe the mesh of prescribed flux elements
 void actions_before_adapt();
 
 /// Actions after adapt: Rebuild the mesh of prescribed flux elements
 void actions_after_adapt();
 
 /// Create Poisson flux elements on boundary b of the Mesh pointed
 /// to by bulk_mesh_pt and add them to the Mesh object pointed to by 
 /// surface_mesh_pt
 void create_flux_elements(const unsigned &b, Mesh* const &bulk_mesh_pt,
                           Mesh* const &surface_mesh_pt);
 
 /// Delete Poisson flux elements and wipe the surface mesh
 void delete_flux_elements(Mesh* const &surface_mesh_pt);
 
 /// Set pointer to prescribed-flux function for all
 /// elements in the surface mesh
 void set_prescribed_flux_pt();
 
 /// Pointer to the "bulk" mesh
 SimpleRefineableRectangularQuadMesh<ELEMENT>* Bulk_mesh_pt;
 
 /// Pointer to the "surface" mesh
 Mesh* Surface_mesh_pt;
 
 /// Pointer to source function
 PoissonEquations<2>::PoissonSourceFctPt Source_fct_pt;
 
}; // end of problem class

[See the discussion of the 1D Poisson problem for a more detailed discussion of the function type PoissonEquations<2>::PoissonSourceFctPt.]

The Problem constructor

We create the bulk mesh and surface mesh as before. Next we create the spatial error estimator and pass it to the bulk mesh.

//=======start_of_constructor=============================================
/// Constructor for Poisson problem: Pass pointer to source function.
//========================================================================
template<class ELEMENT>
RefineableTwoMeshFluxPoissonProblem<ELEMENT>::
RefineableTwoMeshFluxPoissonProblem(PoissonEquations<2>::PoissonSourceFctPt source_fct_pt)
 :  Source_fct_pt(source_fct_pt)
{ 
 
 // Setup "bulk" mesh
 
 // # of elements in x-direction
 unsigned n_x=4;
 
 // # of elements in y-direction
 unsigned n_y=4;
 
 // Domain length in x-direction
 double l_x=1.0;
 
 // Domain length in y-direction
 double l_y=2.0;
 
 // Build "bulk" mesh
 Bulk_mesh_pt=new 
  SimpleRefineableRectangularQuadMesh<ELEMENT>(n_x,n_y,l_x,l_y);
 
 // Create/set error estimator
 Bulk_mesh_pt->spatial_error_estimator_pt()=new Z2ErrorEstimator;

Apart from this, the problem is constructed as in the non-adaptive previous example.

  
 // Create "surface mesh" that will contain only the prescribed-flux 
 // elements. The constructor just creates the mesh without
 // giving it any elements, nodes, etc.
 Surface_mesh_pt = new Mesh;
 
 // Create prescribed-flux elements from all elements that are 
 // adjacent to boundary 1, but add them to a separate mesh.
 // Note that this is exactly the same function as used in the 
 // single mesh version of the problem, we merely pass different Mesh pointers.
 create_flux_elements(1,Bulk_mesh_pt,Surface_mesh_pt);
 
 // Add the two sub meshes to the problem
 add_sub_mesh(Bulk_mesh_pt);
 add_sub_mesh(Surface_mesh_pt);
 
 // Rebuild the Problem's global mesh from its various sub-meshes
 build_global_mesh();
 
 
 // Set the boundary conditions for this problem: All nodes are
 // free by default -- just pin the ones that have Dirichlet conditions
 // here. 
 unsigned n_bound = Bulk_mesh_pt->nboundary();
 for(unsigned b=0;b<n_bound;b++)
  {
   //Leave nodes on boundary 1 free
   if (b!=1)
    {
     unsigned n_node = Bulk_mesh_pt->nboundary_node(b);
     for (unsigned n=0;n<n_node;n++)
      {
       Bulk_mesh_pt->boundary_node_pt(b,n)->pin(0); 
      }
    }
  }
 
 // Complete the build of all elements so they are fully functional
 
 // Loop over the Poisson bulk elements to set up element-specific 
 // things that cannot be handled by constructor: Pass pointer to 
 // source function
 unsigned n_element = Bulk_mesh_pt->nelement();
 for(unsigned e=0;e<n_element;e++)
  {
   // Upcast from GeneralisedElement to Poisson bulk element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(Bulk_mesh_pt->element_pt(e));
 
   //Set the source function pointer
   el_pt->source_fct_pt() = Source_fct_pt;
  }
 
 // Set pointer to prescribed flux function for flux elements
 set_prescribed_flux_pt();
 
 // Setup equation numbering scheme
 cout <<"Number of equations: " << assign_eqn_numbers() << std::endl; 
 
} // end of constructor

Actions before adaptation

The mesh adaptation is driven by the error estimates in the bulk elements and only performed for that mesh. The flux elements must therefore be removed before adaptation. We do this by calling the function delete_flux_elements(...), and then rebuilding the Problem's global mesh.

//=====================start_of_actions_before_adapt======================
/// Actions before adapt: Wipe the mesh of prescribed flux elements
//========================================================================
template<class ELEMENT>
void RefineableTwoMeshFluxPoissonProblem<ELEMENT>::actions_before_adapt()
{
 // Kill the flux elements and wipe surface mesh
 delete_flux_elements(Surface_mesh_pt);
 
 // Rebuild the Problem's global mesh from its various sub-meshes
 rebuild_global_mesh();
 
}// end of actions_before_adapt

Actions after adapt

After the (bulk-)mesh has been adapted, the flux elements must be re-attached. This is done by calling the function create_flux_elements(...), followed by a rebuild of the Problem's global mesh. Finally, we set the function pointer to the prescribed flux function for each flux element.

//=====================start_of_actions_after_adapt=======================
///  Actions after adapt: Rebuild the mesh of prescribed flux elements
//========================================================================
template<class ELEMENT>
void RefineableTwoMeshFluxPoissonProblem<ELEMENT>::actions_after_adapt()
{
 // Create prescribed-flux elements from all elements that are 
 // adjacent to boundary 1 and add them to surfac mesh
 create_flux_elements(1,Bulk_mesh_pt,Surface_mesh_pt);
 
 // Rebuild the Problem's global mesh from its various sub-meshes
 rebuild_global_mesh();
 
 // Set pointer to prescribed flux function for flux elements
 set_prescribed_flux_pt();
 
 // Doc refinement levels in bulk mesh
 unsigned min_refinement_level;
 unsigned max_refinement_level;
 Bulk_mesh_pt->get_refinement_levels(min_refinement_level,
                                     max_refinement_level); 
 cout << "Min/max. refinement levels in bulk mesh: " 
      << min_refinement_level << " " 
      << max_refinement_level << std::endl;
 
}// end of actions_after_adapt

Delete flux elements

This function loops over all the flux elements (i.e. those in the surface mesh) and deletes them and their storage.

//============start_of_delete_flux_elements==============================
/// Delete Poisson Flux Elements and wipe the surface mesh
//=======================================================================
template<class ELEMENT>
void RefineableTwoMeshFluxPoissonProblem<ELEMENT>::
delete_flux_elements(Mesh* const &surface_mesh_pt)
{
 // How many surface elements are in the surface mesh
 unsigned n_element = surface_mesh_pt->nelement();
 
 // Loop over the surface elements
 for(unsigned e=0;e<n_element;e++)
  {
   // Kill surface element
   delete surface_mesh_pt->element_pt(e);
  }
 
 // Wipe the mesh
 surface_mesh_pt->flush_element_and_node_storage();
 
} // end of delete_flux_elements

IMPORTANT: Note how the elements are first deleted "manually" and then "flushed" from the surface mesh, using the function Mesh::flush_element_and_node_storage(). This is necessary because deleting the surface mesh directly (by delete surface_mesh_pt;) would also delete its constituent Nodes which are shared with the bulk mesh and must therefore be retained!

Actions before solve

This remains as before.

Post-processing

This remains as before.

Create flux elements

This remains as before.

Source files for this tutorial

The source files for this tutorial are located in the directory: demo_drivers/poisson/two_d_poisson_flux_bc_adapt/
The driver code is: demo_drivers/poisson/two_d_poisson_flux_bc_adapt/two_d_poisson_flux_bc_adapt.cc

PDF file

A pdf version of this document is available.