Optimisation

One of the main challenges in the development of a general-purpose scientific computing library is the potential conflict between the desire for robustness and generality on the one hand, and code optimisation (in terms of speed and memory requirements) on the other.

One of oomph-lib's main design principles is that

Robustness/correctness is more important than "raw speed",

implying that by default, all methods should reliably produce the correct results. Possible optimisations that may lead to incorrect results even for a small subset of cases, must be activated explicitly by the "knowledgeable" user, who then takes the responsibility for any resulting errors.

Here are some examples for possible optimisations that you may wish to activate for your problem.

All tend to lead to faster run times (by how much depends on your machine and your compiler – experiment!), but there are caveats that you must be aware of:

  • Some techniques may incur significant memory overheads (e.g. storing the shape functions).
  • Some techniques may produce the wrong results for your problem (for instance, declaring a problem to be linear when it isn't will lead to a very significant speedup. However, the results will be wrong!)
  • Some techniques will make the code less robust (e.g. using C-style output).

You choose!

Linear vs. nonlinear problems

By default, oomph-lib treats all problems as nonlinear and uses Newton's method to solve the system of nonlinear algebraic equations that result from the problem's discretisation. With this approach, linear problems are special cases for which Newton's method converges in one step. However, if a problem is known to be linear, several (costly) steps in Newton's method are superfluous and may be omitted, leading to a significant speedup. For instance, in a linear problem it is not necessary to re-compute the residuals of the nonlinear algebraic equations after the (single) Newton step, as we already know that they will have been reduced to zero (modulo roundoff errors). We refer to the document "Action" functions in oomph-lib's black-box Newton solver for a more detailed discussion.

The user may declare a problem to be linear by setting the flag

bool Problem::Problem_is_nonlinear

which is initialised to true in the constructor of the Problem base class, to false.

Experiment with the demo code two_d_poisson.cc to examine the speedup achievable by declaring a (linear!) Problem to be linear.

Storing the shape functions

If a problem is to be solved repeatedly (e.g. in a time-dependent simulation, or during a parameter study) it may be beneficial to avoid the re-computation of the shape function and their derivatives with respect to the local and global coordinates at the elements' integration points by storing their values.

However, there are two problems with this approach:

  1. It introduces significant memory overheads. For instance, to store just the shape functions in a 3D problem discretised by 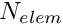$ N_{elem}$ 27-node brick elements with a 27-point Gauss rule, storage for 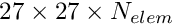$ 27 \times 27 \times N_{elem} $ doubles is required. Storage of the (much more costly to compute) shape function derivatives requires six times that storage.
  2. The most costly-to-compute quantities are the derivatives of the shape functions with respect to the global coordinates, so it is most tempting to store these. However, in free-boundary problems in which the nodal positions are determined as part of the solution, the derivatives of the shape functions with respect to the global coordinates depend on the solution and must be recomputed.

To ensure correctness/robustness and to minimise the memory overheads, oomph-lib's existing finite elements represent the shape functions and their derivatives as StorableShapeFunction objects. These allow their values to be stored at the integration points, but the capability is not activated, unless an element (of type ELEMENT, say) is used in its "wrapped" form, as StorableShapeElement<ELEMENT>.

The detailed documentation for this is yet to be written but you may consult the well-documented demo code two_d_poisson_stored_shape_fcts.cc, and the discussion in the (Not-So-)Quick Guide.

Full vs. reduced integration

To maximise the potential for code reuse, all existing finite elements in oomph-lib are composed (via multiple inheritance) from (i) "geometric" finite elements (e.g. line, quad, brick, triangle and tet elements), and (ii) separate equations classes. A default (spatial) integration scheme is defined for each geometric element. This default integration scheme is chosen to provide "full integration" for this element. This implies that for an undeformed element the products of any two shape functions are integrated exactly. For time-dependent problems (e.g. in problems involving the unsteady heat equation) where products of shape functions arise in the "mass matrix", "full integration" is required to ensure that the numerical solution converges to the exact solution under mesh refinement. In some applications (e.g. in problems involving the Poisson equation) a lower-order (and therefore cheaper) "reduced integration" scheme may be sufficient to maintain the asymptotic convergence rate.

In this case, the user can over-write the default spatial integration scheme, using the function FiniteElement::set_integration_scheme(...), as illustrated here.

// Create an instance of a lower-order integration scheme
Gauss<2,2>* int_pt=new Gauss<2,2>;
//Find number of elements in mesh
unsigned n_element = problem.mesh_pt()->nelement();
// Loop over the elements
for(unsigned i=0;i<n_element;i++)
{
//Set the a different integration scheme
problem.mesh_pt()->finite_element_pt(i)->set_integration_scheme(int_pt);
}

Driver codes that may be used to experiment with reduced integration and to assess the asymptotic convergence behaviour can be found in the directory self_test/poisson/convergence_tests/

Disabling the ALE formulation of unsteady equations

Most existing finite elements for unsteady problems are formulated in the "Arbitrary Lagrangian Eulerian (ALE)" form by implementing the Eulerian time-derivative $ \partial u /\partial t$ (to be evaluated at a fixed Eulerian position) as

\[ \left. \frac{\partial u}{\partial t} \right|_{\mbox{fixed Eulerian position}} = \left. \frac{\partial u}{\partial t} \right|_{\mbox{fixed local coordinate}} - \sum_{i=1}^{DIM} v_i^{\mbox{[Mesh]}} \ \frac{\partial u}{\partial x_i} \]

where $ v_i^{\mbox{[Mesh]}} \ \ (i=1,...,DIM)$ is the mesh velocity. This formulation ensures that the time-derivatives are computed correctly if the element is used in a free-boundary value problem. However, the computation of the mesh velocities introduces an additional cost which is avoidable if the mesh is, in fact, stationary. The user may disable the computation of the ALE terms by calling the function

FiniteElement::disable_ALE()

(This function is implemented as a virtual function in the FiniteElement base class. If called, it simply issues a warning message to announce that it has not been overloaded in a derived class – usually an indication that the element in question does not involve any ALE terms). The ALE capability may be re-enabled by calling the corresponding function

FiniteElement::enable_ALE()

Experiment with the driver codes in the directory demo_drivers/optimisation/disable_ALE to examine the speedup achievable by ignoring the ALE terms in the unsteady heat and Navier-Stokes equations.

C vs. C++-style output

In most demo driver codes post-processing is performed by passing a C++-stream to a high-level output function, as in this code segment

#include<ofstream>
[...]
ofstream output_stream("solution.dat");
mesh_pt()->output(output_stream);
output_stream.close();
[...]

While C++-streams are very convenient, they can be expensive – so much so that in extreme cases a computation can become dominated by the cost of the post-processing operations. There is no obvious reason why I/O with C++ streams should be so much slower than I/O in fortran or C, say. In fact, it is not supposed to be! (Google will lead you to numerous heated discussions on this topic.) However, we (and, it seems, many others) have found C++-output to be consistently slower than C-style output. Since the latter is available from C++ we have started to provide alternative output routines that employ C-style I/O, using the FILE type. If your computation involves lots of I/O, it may be helpful to replace the above statements by

#include<stdio.h>
[...]
FILE* file_pt = fopen("solution.dat","w");
mesh_pt()->output(file_pt);
fclose(file_pt);
[...]

Depending on the application, we typically find that C-style output is about 2 to 6 times faster than its C++ equivalent. Run the demo code c_style_output.cc to explore the relative performance of the two methods on your machine. However, C-style output is not as "bullet-proof" as its C++-counterpart. For instance, if an output directory does not exist, trying to write to it with C-style output tends to cause a segmentation fault, whereas C++-output handles this more gracefully (no output is produced but the code execution continues).

Different sparse assembly techniques and the STL memory pool

The different sparse assembly methods and how to compare their relative performance

oomph-lib's black-box nonlinear solver Problem::newton_solve() employs Newton's method to solve the system of nonlinear algebraic equations arising from the discretisation of the problem. By default, the linear systems that determine the corrections to the unknowns during the Newton iterations are solved with SuperLUSolver, oomph-lib's default LinearSolver. Within this framework the two most computationally expensive steps (both in terms of memory usage and CPU time) are the assembly of the linear system (comprising the Jacobian matrix and the residual vector) and its solution. [Not all of oomph-lib's LinearSolvers require the assembly of the Jacobian matrix (for instance the frontal solver HSL_MA42 avoids the assembly of the linear system and computes its LU decomposition "on the fly") but most of them do.]

The assembly of the Jacobian matrix (in compressed-row or compressed-column storage) is typically performed by the function

Problem::sparse_assemble_row_or_column_compressed(...)

This function performs the assembly, using one of five different assembly methods, selected by the protected member data

unsigned Problem::Sparse_assembly_method

in the Problem class. This flag can take any of the values defined in the enumeration Problem::Assembly_method.

Each of the five different methods has its own advantages and disadvantages in terms of speed and/or memory requirements. By default, we use the "assembly using vectors of pairs" as it tends to be optimal in both respects – at least when the library is compiled with full optimisation. If the library is compiled without optimisation and/or in PARANOID mode, the map-based assembly tends to be faster, if significantly more expensive in terms of memory requirements.

You should explore the performance of the various methods on your machine, using the the driver code sparse_assemble_test.cc in the directory

demo_drivers/optimisation/sparse_assemble

The shell script compare.bash in the same directory may be used to systematically explore the performance of the different methods for various problem sizes.

While the test code automatically documents the CPU times required for the matrix assembly, the automatic assessment of its memory usage is a somewhat nontrivial task. We provide a quick-and-dirty solution to this problem: If the protected member data

bool Problem::Pause_at_end_of_sparse_assembly

is set to true, the assembly process is halted when it has reached its most memory-intensive phase. The user can then use top (or some other external tool) to assess the memory usage of the code. (Typing "M" in top sorts the entries by memory usage rather than by cpu usage).

The STL memory pool

When analysing the code's memory usage, you may notice that, following the assembly of the Jacobian matrix, not all memory is returned to the system, particularly, if maps or lists are used for the assembly. This does not indicate the presence of a memory leak but is a result of the internal memory management performed by the STL allocator which retains some (and in some cases a lot) of the initially allocated memory in its own "memory pool" in order to speed up the subsequent memory allocation for other STL objects. Google for "STL memory pool" to find out more about this issue. The executive summary is: "Memory pools are good for you", even though they have the slightly annoying side-effect of making it virtually impossible to monitor the actual memory usage of the code.

PDF file

A pdf version of this document is available.