In this document, we discuss an alternative approach for solving the 2D Poisson problem:

Two-dimensional model Poisson problem with Neumann boundary conditions Solve

$\sum_{i=1}^2 \frac{\partial^2u}{\partial x_i^2} = f(x_1,x_2), \ \ \ \ \ \ \ \ \ \ (1)$

in the rectangular domain $D = \left\{ (x_1,x_2) \in [0,1] \times [0,2]\right\}$ . The domain boundary $\partial D = \partial D_{Neumann} \cup \partial D_{Dirichlet}$ , where $\partial D_{Neumann} = \left\{ (x_1,x_2) | x_1=1, \ x_2\in [0,2] \right\}$ . On $\partial D_{Dirichlet}$ we apply the Dirichlet boundary conditions

$\left. u\right|_{\partial D_{Dirichlet}}=u_0, \ \ \ \ \ \ \ \ \ \ (2)$

where the function

is given. On $\partial D_{Neumann}$ we apply the Neumann conditions

$\left. \frac{\partial u}{\partial n}\right|_{\partial D_{Neumann}} = \left. \frac{\partial u}{\partial x_1}\right|_{\partial D_{Neumann}} =g_0, \ \ \ \ \ \ \ \ \ \ (3)$

where the function

is given.

In a previous example, we applied the Neumann boundary conditions by adding PoissonFluxElements (elements that apply the Neumann (flux) boundary conditions on surfaces of higher-dimensional "bulk" Poisson elements) to the Problem's Mesh object. The ability to combine elements of different types in a single Mesh object is convenient, and in certain circumstances absolutely essential, but it can cause problems; see the discussion of the doc_solution(...) function in the previous example. Furthermore, it seems strange (if not wrong!) that the SimpleRectangularQuadMesh – an object that is templated by a particular (single!) element type – also contains elements of a different type.

We shall now demonstrate an alternative approach, based on the use of multiple meshes, each containing only one type of element. The ability to use multiple Meshes in a single Problem is an essential feature of oomph-lib and is vital in fluid-structure interaction problems, where the fluid and solid domains are distinct and each domain is discretised by a different element type.

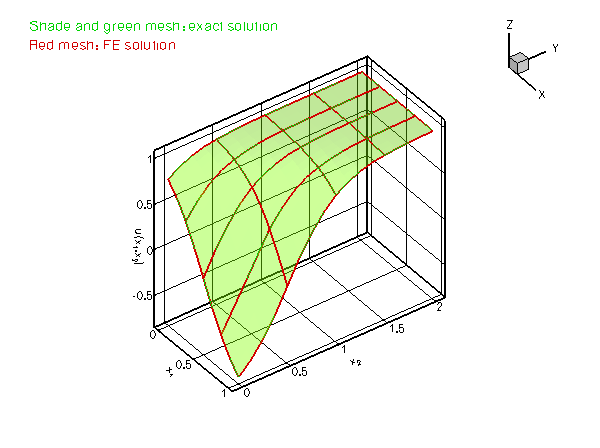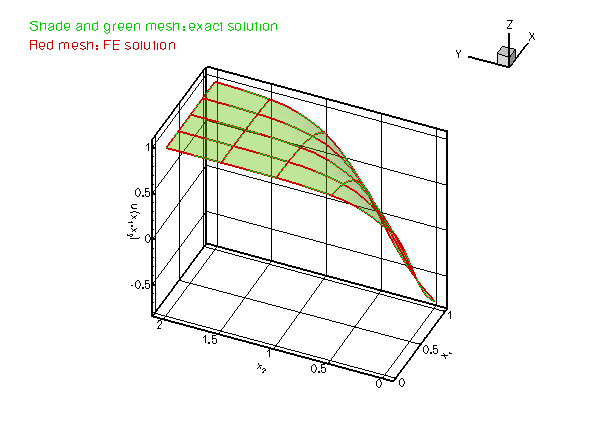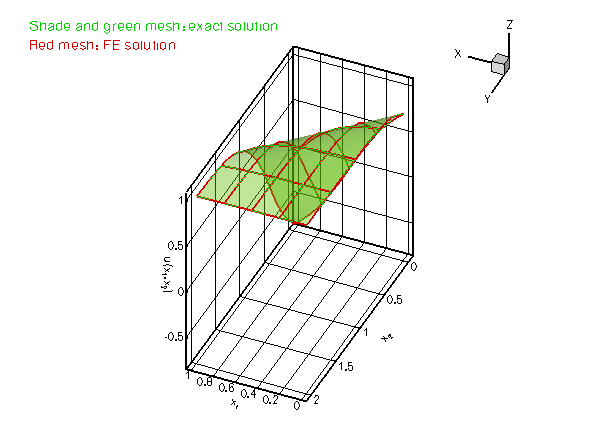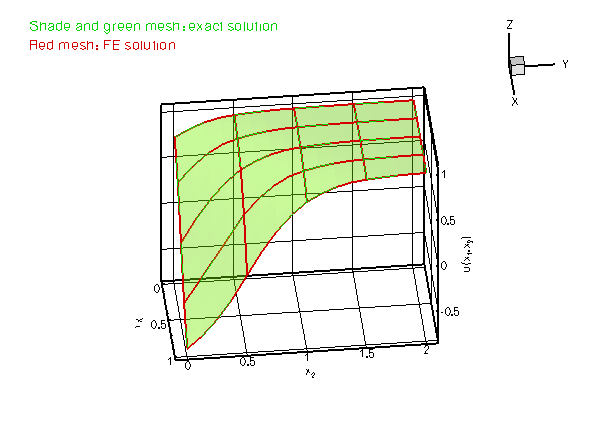
We consider the same problem as in the previous example and choose a source function and boundary conditions for which the function

$u_0(x_1,x_2) = \tanh(1-\alpha(x_1 \tan\Phi - x_2)), \ \ \ \ \ \ \ \ \ (4)$

is the exact solution of the problem.

Plot of the solution

Global parameters and functions

The specification of the source function and the exact solution in the namespace TanhSolnForPoisson is identical to that in the single-mesh version discussed in the previous example.

The driver code

The driver code is identical to that in the single-mesh version discussed in the previous example.

The problem class

The problem class is virtually identical to that in the single-mesh implementation: The only difference is that we store pointers to the two separate Mesh objects as private member data, and provide a slightly different implementation of the function create_flux_elements(...).

//========= start_of_problem_class=====================================
/// 2D Poisson problem on rectangular domain, discretised with
/// 2D QPoisson elements. Flux boundary conditions are applied
/// along boundary 1 (the boundary where x=L). The specific type of 
/// element is specified via the template parameter.
//====================================================================
template<class ELEMENT> 
class TwoMeshFluxPoissonProblem : public Problem
{
 
public:
 
 /// Constructor: Pass pointer to source function
 TwoMeshFluxPoissonProblem(PoissonEquations<2>::PoissonSourceFctPt source_fct_pt);
 
 /// Destructor (empty)
 ~TwoMeshFluxPoissonProblem(){}
 
 /// Doc the solution. DocInfo object stores flags/labels for where the
 /// output gets written to
 void doc_solution(DocInfo& doc_info);
 
 
private:
 
 /// Update the problem specs before solve: Reset boundary conditions
 /// to the values from the exact solution.
 void actions_before_newton_solve();
 
 /// Update the problem specs after solve (empty)
 void actions_after_newton_solve(){}
 
 /// Create Poisson flux elements on boundary b of the Mesh pointed
 /// to by bulk_mesh_pt and add them to the Mesh object pointed to by 
 /// surface_mesh_pt
 void create_flux_elements(const unsigned &b, Mesh* const &bulk_mesh_pt,
                           Mesh* const &surface_mesh_pt);
 
 /// Pointer to the "bulk" mesh
 SimpleRectangularQuadMesh<ELEMENT>* Bulk_mesh_pt;
 
 /// Pointer to the "surface" mesh
 Mesh* Surface_mesh_pt;
 
 /// Pointer to source function
 PoissonEquations<2>::PoissonSourceFctPt Source_fct_pt;
 
}; // end of problem class

[See the discussion of the 1D Poisson problem for a more detailed discussion of the function type PoissonEquations<2>::PoissonSourceFctPt.]

The Problem constructor

As before we start by creating the "bulk" mesh and store a pointer to this mesh in the private data member TwoMeshFluxPoissonProblem::Bulk_mesh_pt:

//=======start_of_constructor=============================================
/// Constructor for Poisson problem: Pass pointer to source function.
//========================================================================
template<class ELEMENT>
TwoMeshFluxPoissonProblem<ELEMENT>::
TwoMeshFluxPoissonProblem(PoissonEquations<2>::PoissonSourceFctPt source_fct_pt)
 :  Source_fct_pt(source_fct_pt)
{ 
 // Setup "bulk" mesh
 
 // # of elements in x-direction
 unsigned n_x=4;
 
 // # of elements in y-direction
 unsigned n_y=4;
 
 // Domain length in x-direction
 double l_x=1.0;
 
 // Domain length in y-direction
 double l_y=2.0;
 
 // Build "bulk" mesh
 Bulk_mesh_pt=new SimpleRectangularQuadMesh<ELEMENT>(n_x,n_y,l_x,l_y);

Next, we construct an (empty) Mesh and store a pointer to it in the private data member TwoMeshFluxPoissonProblem::Surface_mesh_pt.

 // Create "surface mesh" that will contain only the prescribed-flux 
 // elements. The constructor just creates the mesh without
 // giving it any elements, nodes, etc.
 Surface_mesh_pt = new Mesh;

We use the function create_flux_elements(...), to create the prescribed-flux elements for the elements on boundary 1 of the bulk mesh and add them to the surface mesh.

 // Create prescribed-flux elements from all elements that are 
 // adjacent to boundary 1, but add them to a separate mesh.
 // Note that this is exactly the same function as used in the 
 // single mesh version of the problem, we merely pass different Mesh pointers.
 create_flux_elements(1,Bulk_mesh_pt,Surface_mesh_pt);

We have now created all the required elements and can access them directly via the two data members TwoMeshFluxPoissonProblem::Bulk_mesh_pt and TwoMeshFluxPoissonProblem::Surface_mesh_pt. However, many of oomph-lib's generic procedures require ordered access to all of the Problem's elements, nodes, etc. For instance, Problem::newton_solve(...) computes the entries in the global Jacobian matrix by adding the contributions from all elements in all (sub-)meshes. Ordered access to the Problem's elements, nodes, etc is generally obtained via the Problem's (single!) global Mesh object, which is accessible via Problem::mesh_pt(). The Problem base class also provides a private data member Problem::Sub_mesh_pt (a vector of type Vector<Mesh*>) which stores the (pointers to the) Problem's sub-meshes. We must add the pointers to our two sub-meshes to the problem,

 // Add the two sub meshes to the problem
 add_sub_mesh(Bulk_mesh_pt);
 add_sub_mesh(Surface_mesh_pt);

and use the function Problem::build_global_mesh() to combine the Problem's sub-meshes into a single, global Mesh that is accessible via Problem::mesh_pt():

// Combine all submeshes into a single Mesh

build_global_mesh();

The rest of the constructor is identical to that in the single-mesh implementation. We pin the nodal values on the Dirichlet boundaries, pass the function pointers to the elements, and set up the equation numbering scheme:

 // Set the boundary conditions for this problem: All nodes are
 // free by default -- just pin the ones that have Dirichlet conditions
 // here. 
 unsigned n_bound = Bulk_mesh_pt->nboundary();
 for(unsigned b=0;b<n_bound;b++)
  {
   //Leave nodes on boundary 1 free
   if (b!=1)
    {
     unsigned n_node = Bulk_mesh_pt->nboundary_node(b);
     for (unsigned n=0;n<n_node;n++)
      {
       Bulk_mesh_pt->boundary_node_pt(b,n)->pin(0); 
      }
    }
  }
 
 // Complete the build of all elements so they are fully functional
 
 // Loop over the Poisson bulk elements to set up element-specific 
 // things that cannot be handled by constructor: Pass pointer to 
 // source function
 unsigned n_element = Bulk_mesh_pt->nelement();
 for(unsigned e=0;e<n_element;e++)
  {
   // Upcast from GeneralisedElement to Poisson bulk element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(Bulk_mesh_pt->element_pt(e));
 
   //Set the source function pointer
   el_pt->source_fct_pt() = Source_fct_pt;
  }
 
 // Loop over the flux elements to pass pointer to prescribed flux function
 n_element=Surface_mesh_pt->nelement();
 for(unsigned e=0;e<n_element;e++)
  {
   // Upcast from GeneralisedElement to Poisson flux element
   PoissonFluxElement<ELEMENT> *el_pt = 
    dynamic_cast< PoissonFluxElement<ELEMENT>*>(
     Surface_mesh_pt->element_pt(e));
 
   // Set the pointer to the prescribed flux function
   el_pt->flux_fct_pt() = 
    &TanhSolnForPoisson::prescribed_flux_on_fixed_x_boundary;
  }
 
 // Setup equation numbering scheme
 cout <<"Number of equations: " << assign_eqn_numbers() << std::endl; 
 
} // end of constructor

"Actions before solve"

The only (minor) change to Problem::actions_before_newton_solve() is that the nodes on the boundaries of the bulk (!) mesh are now obtained via the Bulk_mesh_pt pointer, rather than from the combined Mesh, pointed to by Problem::mesh_pt(). While this may appear to be a trivial change, it is a potentially important one. Recall that the surface mesh is an instantiation of the Mesh base class. We created the (empty) mesh in the Problem constructor (by calling the default Mesh constructor), and used the function create_flux_elements(...) to add the (pointers to the) prescribed-flux elements to it. The surface mesh therefore does not have any nodes of its own, and its lookup schemes for the boundary nodes have not been set up. The combined mesh, pointed to by Problem::mesh_pt(), therefore only contains the boundary lookup scheme for the bulk mesh. Hence, the combined mesh has four boundaries and their numbers correspond to those in the bulk mesh.

If we had set up the boundary lookup scheme in the surface mesh, the constructor of the combined Mesh, would have concatenated the boundary lookup schemes of the two sub-meshes so that the four boundaries in sub-mesh 0 would have become boundaries 0 to 3 in the combined mesh, while the two boundaries in the surface mesh would have become boundaries 4 and 5 in the combined Mesh. While the conversion is straightforward, it is obvious that Mesh boundaries are best identified via the sub-meshes.

//====================start_of_actions_before_newton_solve=======================
/// Update the problem specs before solve: Reset boundary conditions
/// to the values from the exact solution.
//========================================================================
template<class ELEMENT>
void TwoMeshFluxPoissonProblem<ELEMENT>::actions_before_newton_solve()
{
 // How many boundaries are in the bulk mesh?
 unsigned n_bound = Bulk_mesh_pt->nboundary();
 
 //Loop over the boundaries in the bulk mesh
 for(unsigned i=0;i<n_bound;i++)
  {
   // Only update Dirichlet nodes
   if (i!=1)
    {
     // How many nodes are there on this boundary?
     unsigned n_node = Bulk_mesh_pt->nboundary_node(i);
     
     // Loop over the nodes on boundary
     for (unsigned n=0;n<n_node;n++)
      {
       // Get pointer to node
       Node* nod_pt=Bulk_mesh_pt->boundary_node_pt(i,n);
       
       // Extract nodal coordinates from node:
       Vector<double> x(2);
       x[0]=nod_pt->x(0);
       x[1]=nod_pt->x(1);
       
       // Compute the value of the exact solution at the nodal point
       Vector<double> u(1);
       TanhSolnForPoisson::get_exact_u(x,u);
       
       // Assign the value to the one (and only) nodal value at this node
       nod_pt->set_value(0,u[0]);
      }
    } 
  }
} // end of actions before solve

Post-processing

The post-processing, implemented in doc_solution(...) is now completely straightforward. Since the PoissonFluxElements only apply boundary conditions, they do not have to be included in the plotting or error checking routines, so we perform these only for the elements in the bulk mesh.

//=====================start_of_doc=======================================
/// Doc the solution: doc_info contains labels/output directory etc.
//========================================================================
template<class ELEMENT>
void TwoMeshFluxPoissonProblem<ELEMENT>::doc_solution(DocInfo& doc_info)
{ 
 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned npts;
 npts=5; 
 
 // Output solution 
 //-----------------
 sprintf(filename,"%s/soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Bulk_mesh_pt->output(some_file,npts);
 some_file.close();
 
 // Output exact solution 
 //----------------------
 sprintf(filename,"%s/exact_soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Bulk_mesh_pt->output_fct(some_file,npts,TanhSolnForPoisson::get_exact_u); 
 some_file.close();
 
 
 // Doc error and return of the square of the L2 error
 //---------------------------------------------------
 double error,norm;
 sprintf(filename,"%s/error%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Bulk_mesh_pt->compute_error(some_file,TanhSolnForPoisson::get_exact_u,
                               error,norm); 
 some_file.close();
 
 // Doc L2 error and norm of solution
 cout << "\nNorm of error   : " << sqrt(error) << std::endl; 
 cout << "Norm of solution: " << sqrt(norm) << std::endl << std::endl;
 
 
} // end of doc

Further comments

We mentioned that the Mesh constructor that builds a combined Mesh from a vector of sub-meshes, concatenates the sub-meshes' element, node and boundary lookup schemes. There are a few additional features that the "user" should be aware of:

The sub-meshes should not contain any duplicate nodes or elements. If they do, the function Problem::build_global_mesh() will issue a warning and ignore any duplicates. This is because the Problem's global Mesh object is used by many functions in which operations must be performed exactly once for each node or element. For instance, in time-dependent problems, the function Problem::shift_time_values(), which is called automatically by Problem::unsteady_newton_solve(...), advances all "history values" by one time-level to prepare for the next timestep. If this was done repeatedly for nodes that are common to multiple sub-meshes, the results would be incorrect. If your problem requires a combined mesh in which duplicates are allowed, you must construct this mesh yourself.
Recall that the function Mesh::add_boundary_node() "tells" the mesh's constituent nodes which boundaries they are located on. What happens if a (sub-)mesh for which this lookup scheme has been set up becomes part of a global Mesh? For various (good!) reasons, the Mesh constructor does not update this information. The boundary number stored by the nodes therefore always refers to the boundary in the Mesh that created them. If this is not appropriate for your problem, you must construct the combined mesh yourself.

Source files for this tutorial

The source files for this tutorial are located in the directory: demo_drivers/poisson/two_d_poisson_flux_bc2/
The driver code is: demo_drivers/poisson/two_d_poisson_flux_bc2/two_d_poisson_flux_bc2.cc

PDF file

A pdf version of this document is available.