In this document, we demonstrate how to solve a 2D Poisson problem with Neumann boundary conditions, using existing objects from the oomph-lib library:

Two-dimensional model Poisson problem with Neumann boundary conditions Solve

$\sum_{i=1}^2 \frac{\partial^2u}{\partial x_i^2} = f(x_1,x_2), \ \ \ \ \ \ \ \ \ \ (1)$

in the rectangular domain $D = \left\{ (x_1,x_2) \in [0,1] \times [0,2]\right\}$ . The domain boundary $\partial D = \partial D_{Neumann} \cup \partial D_{Dirichlet}$ , where $\partial D_{Neumann} = \left\{ (x_1,x_2) | x_1=1, \ x_2\in [0,2] \right\}$ . On $\partial D_{Dirichlet}$ we apply the Dirichlet boundary conditions

$\left. u\right|_{\partial D_{Dirichlet}}=u_0, \ \ \ \ \ \ \ \ \ \ (2)$

where the function

is given. On $\partial D_{Neumann}$ we apply the Neumann conditions

$\left. \frac{\partial u}{\partial n}\right|_{\partial D_{Neumann}} = \left. \frac{\partial u}{\partial x_1}\right|_{\partial D_{Neumann}} =g_0, \ \ \ \ \ \ \ \ \ \ (3)$

where the function

is given.

We provide a detailed discussion of the driver code two_d_poisson_flux_bc.cc which solves the problem for

$u_0(x_1,x_2) = \tanh(1-\alpha(x_1 \tan\Phi - x_2)), \ \ \ \ \ \ \ \ \ (4)$

$f(x_1,x_2) = \sum_{i=1}^2 \frac{\partial^2 u_0}{\partial x_i^2}, \ \ \ \ \ \ \ \ \ (5)$

and

$g_0 = \left. \frac{\partial u_0}{\partial n} \right|_{x_1=1} = \left. \frac{\partial u_0}{\partial x_1} \right|_{x_1=1}, \ \ \ \ \ \ \ \ \ (6)$

so that is the exact solution of the problem. For large values of $\alpha$ the solution approaches a step function

$u_{step}(x_1,x_2) = \left\{ \begin{array}{rl} -1 & \mbox {for $x_2 < x_1 \ \tan\Phi$} \\ 1 & \mbox {for $x_2 > x_1 \ \tan\Phi$} \end{array} \right.$

and presents a serious challenge for any numerical method. The figure below compares the numerical and exact solutions for $\alpha = 1$ and $\Phi = 45^o$ .

Plot of the solution

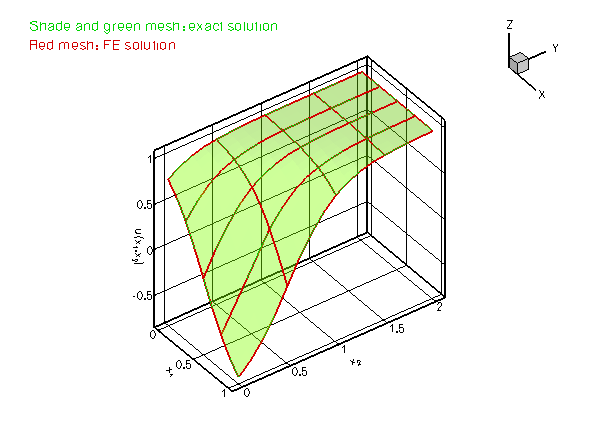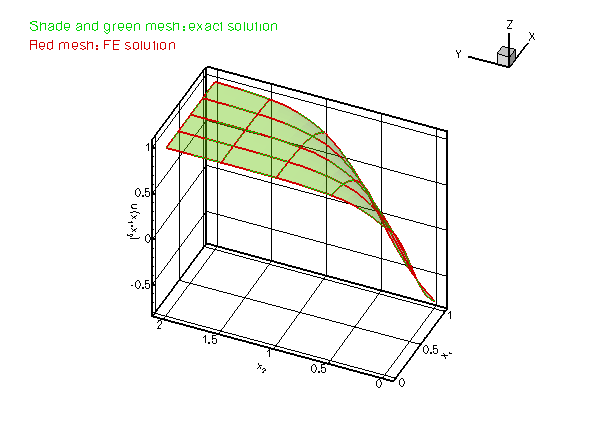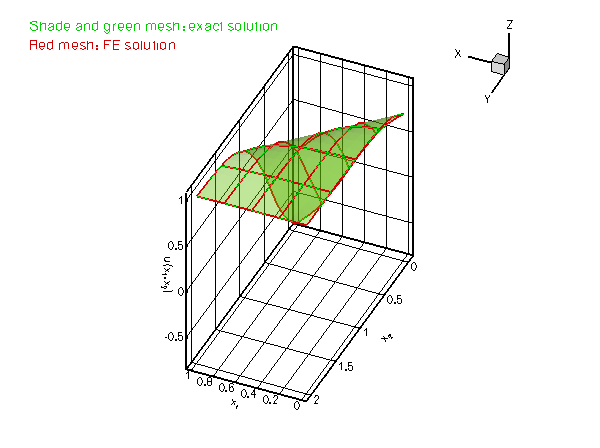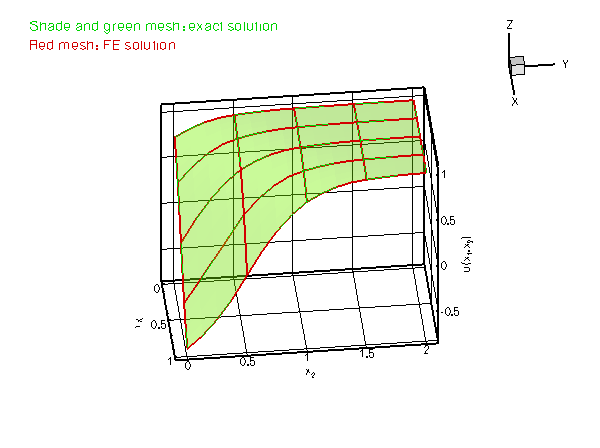
Most of the driver code is identical to the code that solves the equivalent problem without Neumann boundary conditions. Therefore we only provide a detailed discussion of those functions that needed to be changed to accommodate the Neumann boundary conditions.

Global parameters and functions

As in the Dirichlet problem, we define the source function (5) and the exact solution (4), together with the problem parameters $\tan \Phi$ and $\alpha$ , in a namespace TanhSolnForPoisson. We add the function TanhSolnForPoisson::prescribed_flux_on_fixed_x_boundary(...) which computes the prescribed flux required in the Neumann boundary condition (3). The function evaluates $\partial u_0 /\partial n = {\bf N} \cdot \nabla u_0$ for the normal direction specified by the vector ${\bf N} = (1,0)^T.$

//===== start_of_namespace=============================================
/// Namespace for exact solution for Poisson equation with "sharp step" 
//=====================================================================
namespace TanhSolnForPoisson
{
 
 /// Parameter for steepness of "step"
 double Alpha=1.0;
 
 /// Parameter for angle Phi of "step"
 double TanPhi=0.0;
 
 /// Exact solution as a Vector
 void get_exact_u(const Vector<double>& x, Vector<double>& u)
 {
  u[0]=tanh(1.0-Alpha*(TanPhi*x[0]-x[1]));
 }
 
 /// Source function required to make the solution above an exact solution 
 void source_function(const Vector<double>& x, double& source)
 {
  source = 2.0*tanh(-1.0+Alpha*(TanPhi*x[0]-x[1]))*
   (1.0-pow(tanh(-1.0+Alpha*(TanPhi*x[0]-x[1])),2.0))*
   Alpha*Alpha*TanPhi*TanPhi+2.0*tanh(-1.0+Alpha*(TanPhi*x[0]-x[1]))*
   (1.0-pow(tanh(-1.0+Alpha*(TanPhi*x[0]-x[1])),2.0))*Alpha*Alpha;
 }
 
 /// Flux required by the exact solution on a boundary on which x is fixed
 void prescribed_flux_on_fixed_x_boundary(const Vector<double>& x, 
                                          double& flux)
 {
  //The outer unit normal to the boundary is (1,0)
  double N[2] = {1.0, 0.0};
  //The flux in terms of the normal is
  flux = 
   -(1.0-pow(tanh(-1.0+Alpha*(TanPhi*x[0]-x[1])),2.0))*Alpha*TanPhi*N[0]+(
   1.0-pow(tanh(-1.0+Alpha*(TanPhi*x[0]-x[1])),2.0))*Alpha*N[1];
 }
 
} // end of namespace

The driver code

The driver code is very similar to that for the pure Dirichlet problem: We set up the problem, check its integrity and define the problem parameters. Following this, we solve the problem for a number of $\alpha$ values and document the solution.

//==========start_of_main=================================================
/// Demonstrate how to solve 2D Poisson problem with flux boundary 
/// conditions
//========================================================================
int main()
{
 
 //Set up the problem
 //------------------
 
 //Set up the problem with 2D nine-node elements from the
 //QPoissonElement family. Pass pointer to source function. 
 FluxPoissonProblem<QPoissonElement<2,3> > 
  problem(&TanhSolnForPoisson::source_function);
 
 
 // Create label for output
 //------------------------
 DocInfo doc_info;
 
 // Set output directory
 doc_info.set_directory("RESLT");
 
 // Step number
 doc_info.number()=0;
 
 
 
 // Check that we're ready to go:
 //----------------------------
 cout << "\n\n\nProblem self-test ";
 if (problem.self_test()==0) 
  {
   cout << "passed: Problem can be solved." << std::endl;
  }
 else 
  {
   throw OomphLibError("Self test failed",
                       OOMPH_CURRENT_FUNCTION,
                       OOMPH_EXCEPTION_LOCATION);
  }
 
 
 // Set the orientation of the "step" to 45 degrees
 TanhSolnForPoisson::TanPhi=1.0;
 
 // Initial value for the steepness of the "step"
 TanhSolnForPoisson::Alpha=1.0; 
 
 // Do a couple of solutions for different forcing functions
 //---------------------------------------------------------
 unsigned nstep=4;
 for (unsigned istep=0;istep<nstep;istep++)
  {
   // Increase the steepness of the step:
   TanhSolnForPoisson::Alpha+=2.0;
 
   cout << "\n\nSolving for TanhSolnForPoisson::Alpha="
        << TanhSolnForPoisson::Alpha << std::endl << std::endl;
 
   // Solve the problem
   problem.newton_solve();
 
   //Output solution
   problem.doc_solution(doc_info);
 
   //Increment counter for solutions 
   doc_info.number()++; 
  }
 
} //end of main

The problem class

The problem class is virtually identical to that used for the pure Dirichlet problem: The only difference is that the class now contains an additional private data member, FluxPoissonProblem::Npoisson_elements, which stores the number of 2D "bulk" elements in the mesh, and an additional private member function FluxPoissonProblem::create_flux_elements(...). pwd

//========= start_of_problem_class=====================================
/// 2D Poisson problem on rectangular domain, discretised with
/// 2D QPoisson elements. Flux boundary conditions are applied
/// along boundary 1 (the boundary where x=L). The specific type of 
/// element is specified via the template parameter.
//====================================================================
template<class ELEMENT> 
class FluxPoissonProblem : public Problem
{
 
public:
 
 /// Constructor: Pass pointer to source function
 FluxPoissonProblem(PoissonEquations<2>::PoissonSourceFctPt source_fct_pt);
 
 /// Destructor (empty)
 ~FluxPoissonProblem(){}
 
 /// Doc the solution. DocInfo object stores flags/labels for where the
 /// output gets written to
 void doc_solution(DocInfo& doc_info);
 
private:
 
 /// Update the problem specs before solve: Reset boundary conditions
 /// to the values from the exact solution.
 void actions_before_newton_solve();
 
 /// Update the problem specs after solve (empty)
 void actions_after_newton_solve(){}
 
 /// Create Poisson flux elements on the b-th boundary of the 
 /// problem's mesh
 void create_flux_elements(const unsigned &b);
 
 /// Number of Poisson "bulk" elements (We're attaching the flux 
 /// elements to the bulk mesh --> only the first Npoisson_elements elements
 /// in the mesh are bulk elements!)
 unsigned Npoisson_elements;
 
 /// Pointer to source function
 PoissonEquations<2>::PoissonSourceFctPt Source_fct_pt;
 
}; // end of problem class

[See the discussion of the 1D Poisson problem for a more detailed discussion of the function type PoissonEquations<2>::PoissonSourceFctPt.]

The Problem constructor

The first part of the Problem constructor is identical to that used for the pure Dirichlet problem: We create a 2D Mesh consisting of 4x4 quadrilateral Poisson elements:

//=======start_of_constructor=============================================
/// Constructor for Poisson problem: Pass pointer to source function.
//========================================================================
template<class ELEMENT>
FluxPoissonProblem<ELEMENT>::
      FluxPoissonProblem(PoissonEquations<2>::PoissonSourceFctPt source_fct_pt)
       :  Source_fct_pt(source_fct_pt)
{ 
 
 // Setup mesh
 
 // # of elements in x-direction
 unsigned n_x=4;
 
 // # of elements in y-direction
 unsigned n_y=4;
 
 // Domain length in x-direction
 double l_x=1.0;
 
 // Domain length in y-direction
 double l_y=2.0;
 
 // Build and assign mesh
 Problem::mesh_pt()=new SimpleRectangularQuadMesh<ELEMENT>(n_x,n_y,l_x,l_y);

Before continuing, we store the number of 2D "bulk" Poisson elements in the variable FluxPoissonProblem::Npoisson_element:

// Store number of Poisson bulk elements (= number of elements so far).

Npoisson_elements=mesh_pt()->nelement();

Now, we need to apply the prescribed-flux boundary condition along the Neumann boundary $\partial D_{Neumann}$ . The documentation for the SimpleRectangularQuadMesh shows that this boundary is mesh boundary 1. The necessary steps are performed by the function create_flux_elements(..), described in the section Creating the flux elements below.

 // Create prescribed-flux elements from all elements that are 
 // adjacent to boundary 1 and add them to the (single) global mesh
 create_flux_elements(1);

The rest of the constructor is very similar to its counterpart in the pure Dirichlet problem. First we apply Dirichlet conditions on the remaining boundaries by pinning the nodal values. Next, we finish the problem setup by looping over all "bulk" Poisson elements and set the pointer to the source function. Since we have added the PoissonFluxElements to the Mesh, only the first Npoisson_element elements are "bulk" elements and the loop is restricted to these. We then perform a second loop over the PoissonFluxElements which need to be passed the pointer to the prescribed-flux function TanhSolnForPoisson::prescribed_flux_on_fixed_x_boundary(...). Finally, we generate the equation numbering scheme.

 // Set the boundary conditions for this problem: All nodes are
 // free by default -- just pin the ones that have Dirichlet conditions
 // here. 
 unsigned n_bound = mesh_pt()->nboundary();
 for(unsigned b=0;b<n_bound;b++)
  {
   //Leave nodes on boundary 1 free
   if(b!=1)
    {
     unsigned n_node= mesh_pt()->nboundary_node(b);
     for (unsigned n=0;n<n_node;n++)
      {
       mesh_pt()->boundary_node_pt(b,n)->pin(0); 
      }
    }
  }
 
 // Loop over the Poisson bulk elements to set up element-specific 
 // things that cannot be handled by constructor: Pass pointer to source
 // function
 for(unsigned e=0;e<Npoisson_elements;e++)
  {
   // Upcast from GeneralisedElement to Poisson bulk element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(e));
 
   //Set the source function pointer
   el_pt->source_fct_pt() = Source_fct_pt;
  }
 
 // Total number of elements:
 unsigned n_element=mesh_pt()->nelement();
 
 // Loop over the flux elements (located at the "end" of the
 // mesh) to pass function pointer to prescribed-flux function.
 for (unsigned e=Npoisson_elements;e<n_element;e++)
  {
   // Upcast from GeneralisedElement to Poisson flux element
   PoissonFluxElement<ELEMENT> *el_pt = 
    dynamic_cast<PoissonFluxElement<ELEMENT>*>(mesh_pt()->element_pt(e));
 
   // Set the pointer to the prescribed flux function
   el_pt->flux_fct_pt() = 
    &TanhSolnForPoisson::prescribed_flux_on_fixed_x_boundary;
  }
 
 // Setup equation numbering scheme
 cout <<"Number of equations: " << assign_eqn_numbers() << std::endl; 
 
} // end of constructor

Creating the flux elements

oomph-lib provides an element type PoissonFluxElement, which allows the application of Neumann (flux) boundary conditions along the "faces" of higher-dimensional "bulk" Poisson elements. PoissonFluxElements are templated by the type of the corresponding higher-dimensional "bulk" element, so that a PoissonFluxElement<QPoissonElement<2,3> > is a one-dimensional three-node element that applies Neumann boundary conditions along the one-dimensional edge of a nine-node quadrilateral Poisson element. Similarly, a PoissonFluxElement<QPoissonElement<3,2> > is a two-dimensional quadrilateral four-node element that applies Neumann boundary conditions along the two-dimensional face of a eight-node brick-shaped Poisson element; etc.

The constructor of the PoissonFluxElement takes two arguments:

a pointer to the corresponding bulk element
the index face_index of the face that is to be constructed. The convention for two-dimensional Q-type elements is that the face_index is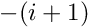 when the coordinate 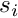is fixed at its minimum value over the face and 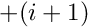when 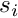is fixed at its maximum value over the face

The layout of the elements in the SimpleRectangularQuadMesh is sufficiently simple to allow the direct determination of the face index: Elements 3, 7, 11 and 15 are located next to mesh boundary 1 and along this boundary the element's local coordinate has a constant (maximum) value of +1.0. Hence we need to set face_index=1

In more complicated meshes, the determination of the face index can be more difficult (or at least very tedious), especially if a Mesh has been refined non-uniformly. The generic Mesh class therefore provides helper functions to determine the required face index for all elements adjacent to a specified Mesh boundary. This allows the creation of the flux elements by the following, completely generic procedure: We use the function Mesh::boundary_element_pt(...) to determine the "bulk" elements that are adjacent to the Neumann boundary, and obtain face_index from the function Mesh::face_index_at_boundary(...). We pass the parameters to the constructor of the PoissonFluxElement and add the (pointer to) the newly created element to the Problem's mesh.

//============start_of_create_flux_elements==============================
/// Create Poisson Flux Elements on the b-th boundary of the Mesh
//=======================================================================
template<class ELEMENT>
void FluxPoissonProblem<ELEMENT>::create_flux_elements(const unsigned &b)
{
 // How many bulk elements are adjacent to boundary b?
 unsigned n_element = mesh_pt()->nboundary_element(b);
 
 // Loop over the bulk elements adjacent to boundary b?
 for(unsigned e=0;e<n_element;e++)
  {
   // Get pointer to the bulk element that is adjacent to boundary b
   ELEMENT* bulk_elem_pt = dynamic_cast<ELEMENT*>(
    mesh_pt()->boundary_element_pt(b,e));
   
   // What is the index of the face of the bulk element at the boundary
   int face_index = mesh_pt()->face_index_at_boundary(b,e);
 
   // Build the corresponding prescribed-flux element
   PoissonFluxElement<ELEMENT>* flux_element_pt = new 
   PoissonFluxElement<ELEMENT>(bulk_elem_pt,face_index);
 
   //Add the prescribed-flux element to the mesh
   mesh_pt()->add_element_pt(flux_element_pt);
 
  } //end of loop over bulk elements adjacent to boundary b
 
} // end of create_flux_elements

"Actions before solve"

The function Problem::actions_before_newton_solve() is identical to that in the
pure Dirichlet problem and is only listed here for the sake of completeness:

//====================start_of_actions_before_newton_solve================
/// Update the problem specs before solve: Reset boundary conditions
/// to the values from the exact solution.
//========================================================================
template<class ELEMENT>
void FluxPoissonProblem<ELEMENT>::actions_before_newton_solve()
{
 // How many boundaries are there?
 unsigned n_bound = mesh_pt()->nboundary();
 
 //Loop over the boundaries
 for(unsigned i=0;i<n_bound;i++)
  {
   // Only update Dirichlet nodes
   if (i!=1)
    {
     // How many nodes are there on this boundary?
     unsigned n_node = mesh_pt()->nboundary_node(i);
     
     // Loop over the nodes on boundary
     for (unsigned n=0;n<n_node;n++)
      {
       // Get pointer to node
       Node* nod_pt = mesh_pt()->boundary_node_pt(i,n);
       
       // Extract nodal coordinates from node:
       Vector<double> x(2);
       x[0]=nod_pt->x(0);
       x[1]=nod_pt->x(1);
       
       // Compute the value of the exact solution at the nodal point
       Vector<double> u(1);
       TanhSolnForPoisson::get_exact_u(x,u);
       
       // Assign the value to the one (and only) nodal value at this node
       nod_pt->set_value(0,u[0]);
      }
    } 
  }
} // end of actions before solve

Post-processing

The post-processing, implemented in doc_solution(...) is similar to that in pure Dirichlet problem. However, since the PoissonFluxElements are auxiliary elements which are only used to apply Neumann boundary conditions on adjacent "bulk" elements, their error checking function is not implemented. We cannot use the generic Mesh member function Mesh::compute_error() to compute an overall error since this function would try to execute the "broken virtual" function GeneralisedElement::compute_error(...); see the section Exercises and Comments for a more detailed discussion of "broken virtual" functions. Error checking would therefore have to be implemented "by hand" (excluding the PoissonFluxElements), or a suitable error measure would have to be defined in the PoissonFluxElements.

We do not pursue either approach here because the difficulty is a direct consequence of our (questionable) decision to include elements of different types in the same Mesh object. While this is perfectly "legal" and often convenient, the practice introduces additional difficulties in refineable problems and we shall demonstrate an alternative approach in another example.

//=====================start_of_doc=======================================
/// Doc the solution: doc_info contains labels/output directory etc.
//========================================================================
template<class ELEMENT>
void FluxPoissonProblem<ELEMENT>::doc_solution(DocInfo& doc_info)
{ 
 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned npts;
 npts=5; 
 
 // Output solution 
 //-----------------
 sprintf(filename,"%s/soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 mesh_pt()->output(some_file,npts);
 some_file.close();
 
 // Output exact solution 
 //----------------------
 sprintf(filename,"%s/exact_soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 for(unsigned e=0;e<Npoisson_elements;e++)
  {
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(e));
   el_pt->output_fct(some_file,npts,TanhSolnForPoisson::get_exact_u); 
  }
 some_file.close();
 
 // Can't use black-box error computatation routines because
 // the mesh contains two different types of elements. 
 // error function hasn't been implemented for the prescribed
 // flux elements...
 
} // end of doc

Exercises and Comments

What happens if you do not create the PoissonFluxElements but leave the nodes on the Neumann boundary un-pinned? Compare the computational result to those obtained when you set the prescribed flux to zero,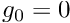 . Does this make sense? [Hint: Remember the "natural" boundary conditions for Poisson's equation].

Try to compute the error of the computed solution by re-instating the global error checking procedure

// Doc error and return of the square of the L2 error
//---------------------------------------------------
double error,norm;
sprintf(filename,"%s/error%i.dat",doc_info.directory().c_str(),
        doc_info.number());
some_file.open(filename);
mesh_pt()->compute_error(some_file,TanhSolnForPoisson::get_exact_u,
                         error,norm); 
some_file.close();

in doc_solution(...). What happens when you run the code? The code's behaviour illustrates a general convention in oomph-lib:

A general convention Some oomph-lib functions, such as GeneralisedElement::compute_error(...), are defined as virtual functions in a base class to allow the implementation of generic procedures such as Mesh::compute_error(...), which loops over all of the Mesh's constituent elements and executes their specific compute_error(...) member functions. In some rare cases (such as the one encountered here), the implementation of a particular virtual function might not be sensible for a specific element. Therefore, rather than forcing the "element-writer" to implement a dummy version of this function in his/her derived class (by declaring it as a pure virtual function in the base class), we provide a "broken virtual" implementation in GeneralisedElement. If the function is (re-)implemented in a derived element, the broken version is ignored; if the function is not overloaded, the broken virtual function throws an error, allowing a traceback in a debugger to find out where the broken function was called from. We note that this practice is not universally approved of in the C++ community but we believe it to have its place in situations such as the one described here.

Incidentally, the code discussed above contains another (possibly more convincing) example of why "broken virtual" functions can be useful. Recall that the creation of the PoissonFluxElements on the Neumann boundary was greatly facilitated by the availability of the helper functions Mesh::boundary_element_pt(...) and
Mesh::face_index_at_boundary(...). These functions are implemented in the generic Mesh base class and determine the relevant parameters via lookup schemes that are stored in that class. Obviously, the lookup schemes need to be set up when a specific Mesh is built and this task can involve a considerable amount of work (see also Setting up the boundary lookup schemes). Since the lookup schemes are useful but by no means essential, the three helper functions are again implemented as broken virtual functions. If the functions are called before the required lookup schemes have been set up, code execution stops with a suitable warning message.

Implement the error computation by hand to familiarise yourself with the way in which the Mesh::compute_error(...) function works.

Setting up the boundary lookup schemes

oomph-lib provides a range of helper functions that set up the boundary lookup schemes for specific Mesh classes. For instance, the QuadMeshBase class forms a base class for all Meshes that consist of two-dimensional quadrilateral elements and has a member function QuadMeshBase::setup_boundary_element_info() which can be called from the constructor of any derived Mesh class to set up the lookup schemes required by Mesh::boundary_element_pt(...) and Mesh::face_index_at_boundary(...).

Source files for this tutorial

The source files for this tutorial are located in the directory: demo_drivers/poisson/two_d_poisson_flux_bc/
The driver code is: demo_drivers/poisson/two_d_poisson_flux_bc/two_d_poisson_flux_bc.cc

PDF file

A pdf version of this document is available.