In this document we discuss the finite-element-based solution of the Helmholtz equation, an elliptic PDE that describes time-harmonic wave propagation problems. We start by reviewing the relevant theory and then present the solution of a simple model problem – the scattering of a planar wave from a circular cylinder.

Acknowledgement: This tutorial and the associated driver codes were developed jointly with Tarak Kharrat (EnstaParisTech, Paris).

Theory: The Helmholtz equation for time-harmonic scattering problems

The Helmholtz equation governs time-harmonic solutions of problems governed by the linear wave equation

$\nabla^2 U(x,y,t) = \frac{1}{c^2} \frac{\partial^2 U(x,y,t)}{\partial t^2}, \ \ \ \ \ \ \ \ \ \ \ \ (1)$

where is the wavespeed. Assuming that is time-harmonic, with frequency $\omega$ , we write the real function as

$U(x,y,t) =Re (u(x,y) \ e^{-i \omega t})$

where is complex-valued. This transforms (1) into the Helmholtz equation

$\nabla^2 u(x,y) + k^2 u(x,y) = 0 \ \ \ \ \ \ \ \ \ \ \ \ (2)$

where

$k = \frac{\omega}{c} \ \ \ \ \ \ \ \ \ \ \ \ (3)$

is the wave number. Like other elliptic PDEs the Helmholtz equation admits Dirichlet, Neumann (flux) and Robin boundary conditions.

If the equation is solved in an infinite domain (e.g. in scattering problems) the solution must satisfy the so-called Sommerfeld radiation condition which in 2D has the form

$\lim_{r\to \infty} \sqrt{r} \left(\frac{\partial u}{\partial r} - iku \right) =0.$

Mathematically, this conditions is required to ensure the uniqueness of the solution (and hence the well-posedness of the problem). In a physical context, such as a scattering problem, the condition ensures that scattering of an incoming wave only produces outgoing not incoming waves from infinity.

Discretisation by finite elements

The discretisation of the Helmholtz equation itself only requires a trivial modification of oomph-lib's Poisson elements – we simply add the term to the residual. Since most practical applications of the Helmholtz equation involve complex-valued solutions, we provide separate storage for the real and imaginary parts of the solution – each Node therefore stores two unknowns values. By default, the real and imaginary parts are stored as values 0 and 1, respectively; see the section The enumeration of the unknowns for details.

The application of Dirichlet and Neumann boundary conditions is straightforward and follows the pattern employed for the solution of the Poisson equation:

Dirichlet conditions are imposed by pinning the relevant nodal values and setting them to the appropriate prescribed values.
Neumann (flux) boundary conditions are imposed via FaceElements (here the HelmholtzFluxElements). As usual we attach these to the faces of the "bulk" elements that are subject to the Neumann boundary conditions.

The imposition of the Sommerfeld radiation condition for problems in infinite domains is slightly more complicated. In the following discussion we will restrict ourselves to two dimensions and assume that the infinite domain is truncated at a circular artificial boundary $\Gamma$ of radius [This assumption is also made in the implementation of oomph-lib's FaceElements that allow the (approximate) imposition of the Sommerfeld radiation condition. The methodology can easily be modified to deal with other geometries but this has not been done yet – any volunteers?] All methods exploit the fact that the relevant solution of the Helmholtz equation can be written in polar coordinates as

$u(r,\varphi) = \sum_{n=-\infty}^{+\infty} A_n \ H_n^{(1)}(kr) \ e^{i n \varphi}, \ \ \ \ \ \ \ (4)$

where the are suitable coefficients and $H_n^{(1)}(r)$ is the -th-order Hankel function of the first kind.

Approximate/absorbing boundary conditions (ABCs)

It is possible to derive approximate versions of the Sommerfeld radiation condition in which the normal derivative of the solution on the artificial boundary is related to its value and possibly its tangential derivatives. Such boundary conditions (sometimes referred to as approximate or absorbing boundary conditions – ABCs) are typically derived from asymptotic expansions of the solution at large distances from the origin and become more accurate the larger the radius of the artificial boundary $\Gamma$ is. Higher accuracy can therefore only be achieved by increasing the size of the computational domain, with an associated increase in computational cost.

oomph-lib provides an implementation of the following three boundary conditions (all taken from J. J. Shirron & I. Babuska's paper "A comparison of approximate boundary conditions and infinite element methods for exterior Helmholtz problems", Computer Methods in Applied Mechanics and Engineering 164 121-139 (1998), in which the authors compare the accuracy of these and many other approximate boundary conditions).

Feng's first order ABC:
$\frac {\partial u}{\partial n}-\bigg( ik - \frac{1}{2R}\bigg) u =0 \mbox{\ \ \ \ \ on\ }\Gamma$
(This is identical to the first-order Bayliss and Turkel boundary condition).
Feng's second order ABC:
$\frac{\partial u}{\partial n}-\bigg[ik-\frac {1}{2R}+\frac{i}{8kR^{2}}\bigg(1+4 \frac {\partial^{2}}{\partial \varphi^{2}}\bigg)\bigg]u =0 \mbox{\ \ \ \ \ on\ }\Gamma$
Feng's third order ABC:
$\frac {\partial u}{\partial n}-\bigg[ik-\frac {1}{2R}+\frac{1}{8k^{2}R^{2}}\bigg(ik+ \frac {1}{R}\bigg) \bigg(1+4 \frac {\partial^{2}}{\partial \varphi^{2}}\bigg)\bigg]u =0 \mbox{\ \ \ \ \ on\ }\Gamma$

All three boundary conditions are implemented in the class HelmholtzAbsorbingBCElement. The order of the approximation can be set via the member function HelmholtzAbsorbingBCElement::abc_order(). All three boundary conditions are local (relating the function to its normal derivative) and do therefore not change the sparsity of the resulting finite element equations.

The Dirichlet-to-Neumann mapping (DtN)

Using (4), it is easy to show (see, e.g., J. Jin "The Finite Element Method in Electromagnetics (second edition)", Wiley (2002) p. 501ff – but note that Jin assumes that the potential varies like $\exp(i\omega t)$ rather than $\exp(-i\omega t)$ as assumed here) that the normal (radial) derivative, $\partial u / \partial n = \partial u / \partial r,$ on the artificial boundary
$\Gamma$ is given by

$\frac {\partial u}{\partial r}\bigg|_{r=R} = \frac {\partial u}{\partial n}\bigg|_{r=R} = \gamma (u) \ \ \ \ \ \ \ (5)$

where

$\gamma (u) = \frac {k}{2 \pi} \sum_{n=-\infty}^{+\infty} \frac {H_n^{(1)^{'}}(kR)}{H_n^{(1)}(kR)} \quad \int_0^{2\pi}u(R,\varphi^{'}) \ e^{in(\varphi-\varphi^{'})} \,d\varphi^{'}. \ \ \ \ \ \ \ (6)$

Equation (5) again provides a condition on the normal derivative of the solution along the artificial boundary and is implemented in the HelmholtzDtNBoundaryElement class. Since $\gamma$ depends on the solution everywhere along the artificial boundary (see (6)), the application of the boundary condition (5) introduces a non-local coupling between all the degrees of freedom located on that boundary. This is handled by classifying the unknowns that affect $\gamma$ but are not associated with the element's own nodes as external Data.

To facilitate the setup of the interaction between the HelmholtzDtNBoundaryElements, oomph-lib provides the class HelmholtzDtNMesh which provides storage for (the pointers to) the HelmholtzDtNBoundaryElements that discretise the artificial boundary. The member function HelmholtzDtNMesh::setup_gamma() pre-computes the $\gamma$ values required for the imposition of equation (5). The radius of the artificial boundary and the (finite) number of (Fourier) terms used in the sum in (6) are specified as arguments to the constructor of the HelmholtzDtNMesh.

NOTE: Since $\gamma$ depends on the solution, it must be recomputed whenever the unknowns are updated during the Newton iteration. This is best done by adding a call to HelmholtzDtNMesh::setup_gamma() to Problem::actions_before_newton_convergence_check(). [If Helmholtz's equation is solved in isolation (or within a coupled, but linear problem), Newton's method will converge in one iteration. In such cases the unnecessary recomputation of $\gamma$ after the one-and-only Newton iteration can be suppressed by setting Problem::Problem_is_nonlinear to false.]

A specific example: Scattering of an acoustic wave from a sound-hard obstacle

We will now demonstrate the methodology for a specific example: the scattering of sound waves in an acoustic medium of density $\rho$ and bulk modulus . Assuming that an incoming sound wave impacts a rigid, impermeable obstacle as shown in this sketch,

Scattering of an incoming wave from a sound-hard obstacle -- the scatterer.

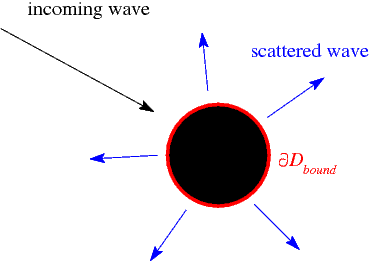
we wish to find the wave field that is scattered from the body.

For this purpose we denote the time-dependent displacement of the fluid particle in the acoustic medium by ${\bf u}^*(x^*,y^*,t^*)$ and introduce a displacement potential $\Phi^*(x^*,y^*,t^*)$ such that

${\bf u}^* = \nabla^* \Phi^*.$

(As usual we employ asterisks to distinguish dimensional quantities from their non-dimensional equivalents, to be introduced below.) It is easy to show that $\Phi^*$ satisfies the linear wave equation (1) with wave speed $c = \sqrt{B/\rho}$ .

Since the surface $\partial D_{bound}$ of the scatterer is impenetrable, the normal displacement of the fluid has to vanish on $\partial D_{bound}$ and the boundary condition for the displacement potential becomes

$\left. \frac{\partial \Phi^*}{\partial n^*}\right|_{\partial D_{bound}} = 0. \ \ \ \ \ \ \ \ \ \ \ \ \ (7)$

We non-dimensionalise all lengths and displacements on some problem-dependent lengthscale ${\cal L}$ (e.g. the radius of the scatterer), non-dimensionalise the potential as $\Phi^* = a^2 \Phi$ and scale time on the period of the oscillation, $t^* = \frac{2\pi}{\omega} t.$ The governing equation then becomes

$\nabla^2 \Phi + k^2 \Phi = 0, \ \ \ \ \ \ \ \ \ \ \ (8)$

where the square of the wavenumber is given by

$k^2 = \frac{\rho (a\omega)^2}{B}.$

Assuming that the incoming wave (already satisfying (8)) is described by a (known) non-dimensional displacement potential of the form

$\Phi_{inc}(x,y,t) = \phi_{inc}(x,y) \ e^{-i 2\pi t},$

we write the total potential as

$\Phi(x,y,t) = \bigg( \phi_{inc}(x,y) + u(x,y) \bigg) \ e^{-i 2\pi t},$

where $u(x,y) \ e^{-i 2\pi t}$ represents the displacement potential associated with the scattered field which must satisfy (2). The boundary condition (7) then becomes a Neumann (flux) boundary condition for the scattered field,

$\left. \frac{\partial u}{\partial n}\right|_{\partial D_{bound}} = - \left. \frac{\partial \phi_{inc}}{\partial n}\right|_{\partial D_{bound}}. \ \ \ \ \ \ \ \ \ \ \ \ \ (9)$

For the special case of the incoming wave being a planar wave, propagating along the x-axis, the incoming field can be written in polar coordinates as

$\phi_{inc}(r, \varphi) = \sum_{n=-\infty}^{+\infty} i^n J_n(kr) e^{in\varphi},$

where is the Bessel function of the first kind of order . The exact solution for the scattering of such a wave from a circular disk is given by the series

$u_{ex}(r,\varphi) = -\sum_{n=-\infty}^{+\infty} i^n \frac {H^{'}_{n}(k)}{J^{'}_{n}(k)} H_n(kr) e^{in\varphi}, \ \ \ \ \ \ \ \ \ \ \ \ \ (10)$

where we have chosen the disk's radius, , as the lengthscale by setting ${\cal L} = a$ . In the above expression, denotes the Hankel function of the first kind of order and the prime denotes differentiation with respect to the function's argument.

A quantity that is of particular interest in wave propagation problems is the time-average of the power radiated by the scatterer,

$\overline{\cal P}^* = \frac{\omega}{2\pi} \int_{0}^{2\pi/\omega} {\cal P}^*(t) \ dt^*.$

In the context of an acoustic wave, the total instantaneous power, ${\cal P}^*(t),$ radiated over a closed boundary is

${\cal P}^*(t) = \oint \frac{\partial {\bf u^*} }{\partial t^*} \cdot p^* {\bf n} \ dS^*,$

where the pressure is related to the displacement potential via

$p^* = \rho \omega^2 \Phi^*.$

The non-dimensional time-averaged radiated power can be expressed in terms of the complex potential $\phi$ as

$\overline{\cal P} = \frac{\overline{\cal P}^*}{\rho \omega^3 {\cal L}^4} = \frac{1}{2} \oint\bigg[Im\bigg(\frac{\partial \phi}{\partial n}\bigg) \ Re(\phi) - Re\bigg(\frac{\partial \phi}{\partial n}\bigg) \ Im(\phi) \bigg] \ dS.$

Results

The figure below shows an animation of the displacement potential for scattering from a circular disk for a non-dimensional wavenumber of over one period of the oscillation. The simulation was performed in an annular computational domain, bounded by the outer surface the (unit) disk and an artificial outer boundary of non-dimensional radius The Sommerfeld radiation condition was imposed using the DtN mapping and the simulation was performed with spatial adaptivity (note the non-uniform refinement).

The "carpet plot" compares the exact (green) and computed (red) solutions for the displacement potential. The colours in the contour plot at the bottom of the figure provide an alternative visualisation of the magnitude of the scattered field.

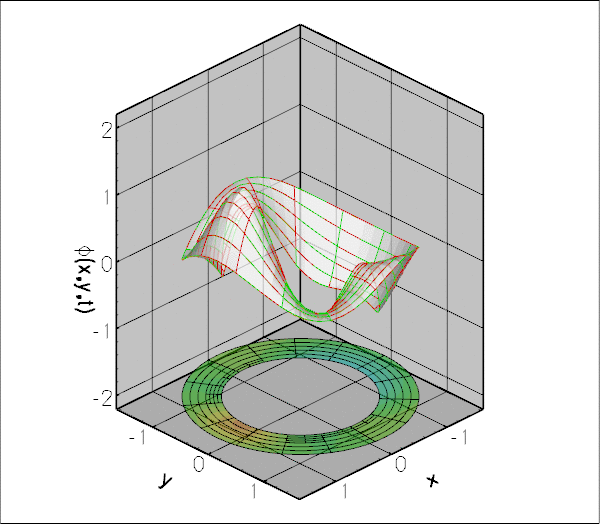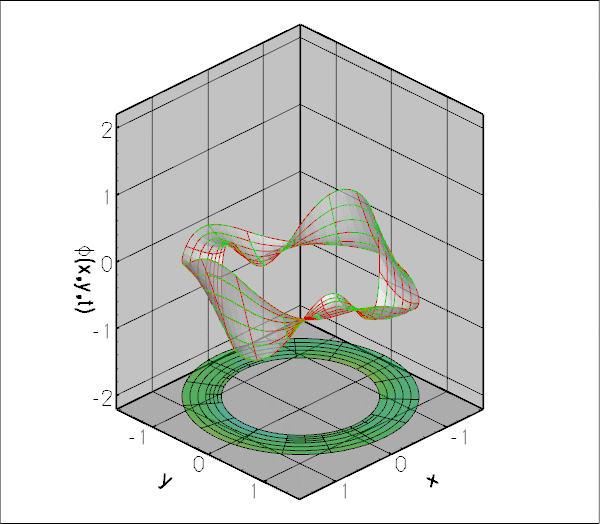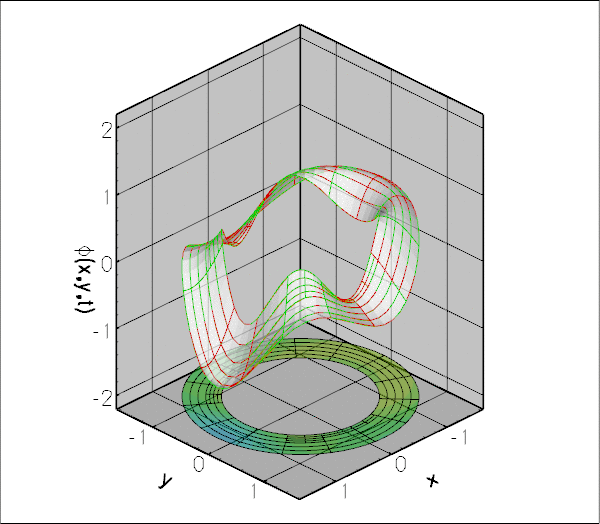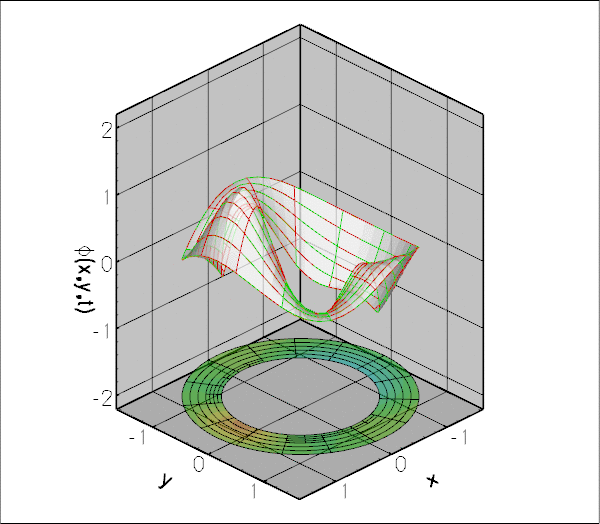
The displacement potential associated with the scattered wave, animated over one period of the oscillation.

The numerical solution

The global namespace

As usual, we define the problem parameters in a global namespace. The main physical parameter is the (square of the) wave number, . N_fourier is the number of (Fourier) terms to be used in evaluation of the series in equations (6) and (10). The remaining parameters determine how the Sommerfeld radiation condition is applied.

//===== start_of_namespace=============================================

The function get_exact_u returns the exact solution for the scattering problem. We will use this function for the validation of our results.

 /// Exact solution for scattered field 
 /// (vector returns real and impaginary parts).
 void get_exact_u(const Vector<double>& x, Vector<double>& u)
 {
  // Switch to polar coordinates
  double r;
  r=sqrt(x[0]*x[0]+x[1]*x[1]);
  double theta;
  theta=atan2(x[1],x[0]);
  
  // Argument for Bessel/Hankel functions
  double rr=sqrt(K_squared)*r;  
 
  // Evaluate Bessel/Hankel functions
  complex <double > u_ex(0.0,0.0);
  Vector<double> jn(N_fourier+1), yn(N_fourier+1),
   jnp(N_fourier+1), ynp(N_fourier+1);
  Vector<double> jn_a(N_fourier+1),yn_a(N_fourier+1),
   jnp_a(N_fourier+1), ynp_a(N_fourier+1);
  Vector<complex<double> > h(N_fourier+1),h_a(N_fourier+1),
   hp(N_fourier+1), hp_a(N_fourier+1);
 
  // We want to compute N_fourier terms but the function
  // may return fewer than that.
  int n_actual=0;
  CRBond_Bessel::bessjyna(N_fourier,sqrt(K_squared),n_actual,
                          &jn_a[0],&yn_a[0],
                          &jnp_a[0],&ynp_a[0]); 
 
  // Shout if things went wrong  
#ifdef PARANOID
  if (n_actual!=int(N_fourier))
   {
    std::ostringstream error_stream; 
    error_stream << "CRBond_Bessel::bessjyna() only computed "
                 << n_actual << " rather than " << N_fourier 
                 << " Bessel functions.\n";    
    throw OomphLibError(error_stream.str(),
                        OOMPH_CURRENT_FUNCTION,
                        OOMPH_EXCEPTION_LOCATION);
   }
#endif
 
  // Evaluate Hankel at actual radius
  Hankel_functions_for_helmholtz_problem::Hankel_first(N_fourier,rr,h,hp);
 
  // Evaluate Hankel at inner (unit) radius
  Hankel_functions_for_helmholtz_problem::Hankel_first(N_fourier
                                                       ,sqrt(K_squared),
                                                       h_a,hp_a);
  
  // Compute the sum: Separate the computation of the negative 
  // and positive terms
  for (unsigned i=0;i<N_fourier;i++)
   {
    u_ex-=pow(I,i)*h[i]*((jnp_a[i])/hp_a[i])*pow(exp(I*theta),i);
   }
  for (unsigned i=1;i<N_fourier;i++)
   {
    u_ex-=pow(I,i)*h[i]*((jnp_a[i])/hp_a[i])*pow(exp(-I*theta),i);
   }
  
  // Get the real & imaginary part of the result
  u[0]=real(u_ex);
  u[1]=imag(u_ex);
  
 }// end of get_exact_u

Next we provide a function that computes the prescribed flux (normal derivative) of the solution, $\partial u/\partial n = -\partial \phi_{inc}/\partial n$ , evaluated on the surface of the unit disk.

 /// Flux (normal derivative) on the unit disk
 /// for a planar incoming wave
 void prescribed_incoming_flux(const Vector<double>& x, 
                               complex<double>& flux)
 {
  // Switch to polar coordinates
  double r;
  r=sqrt(x[0]*x[0]+x[1]*x[1]);
  double theta;
  theta=atan2(x[1],x[0]);
  
  // Argument of the Bessel/Hankel fcts
  double rr=sqrt(K_squared)*r;  
  
  // Compute Bessel/Hankel functions
  Vector<double> jn(N_fourier+1), yn(N_fourier+1),
   jnp(N_fourier+1), ynp(N_fourier+1);
 
  // We want to compute N_fourier terms but the function
  // may return fewer than that.
  int n_actual=0;
  CRBond_Bessel::bessjyna(N_fourier,rr,n_actual,&jn[0],&yn[0],
                          &jnp[0],&ynp[0]);
  
  // Shout if things went wrong...
#ifdef PARANOID
  if (n_actual!=int(N_fourier))
   {
    std::ostringstream error_stream; 
    error_stream << "CRBond_Bessel::bessjyna() only computed "
                 << n_actual << " rather than " << N_fourier 
                 << " Bessel functions.\n";    
    throw OomphLibError(error_stream.str(),
                        OOMPH_CURRENT_FUNCTION,
                        OOMPH_EXCEPTION_LOCATION);
   }
#endif
  
  // Compute the sum: Separate the computation of the negative and 
  // positive terms
  flux=std::complex<double>(0.0,0.0);
  for (unsigned i=0;i<N_fourier;i++)
   {
    flux+=pow(I,i)*(sqrt(K_squared))*pow(exp(I*theta),i)*jnp[i];
   }
  for (unsigned i=1;i<N_fourier;i++)
   {
    flux+=pow(I,i)*(sqrt(K_squared))*pow(exp(-I*theta),i)*jnp[i];
   }
 
 
 }// end of prescribed_incoming_flux 
 
} // end of namespace

The driver code

The driver code is very straightforward. We parse the command line to determine which boundary condition to use and set the flags in the global namespace accordingly.

//==========start_of_main=================================================
/// Solve 2D Helmholtz problem for scattering of a planar wave from a 
/// unit disk 
//========================================================================
int main(int argc, char **argv)
{
 
 // Store command line arguments
 CommandLineArgs::setup(argc,argv);
 
 // Define case to be run
 unsigned i_case=0;
 CommandLineArgs::specify_command_line_flag("--case",&i_case);
 
 // Parse command line
 CommandLineArgs::parse_and_assign(); 
 
 // Doc what has actually been specified on the command line
 CommandLineArgs::doc_specified_flags();
 
 // Now set flags accordingly
 switch(i_case)
  {
  case 0:
   GlobalParameters::DtN_BC=true;
   break;
   
  case 1:
   GlobalParameters::DtN_BC=false;
   GlobalParameters::ABC_order=1;
   break;
 
  case 2:
   GlobalParameters::DtN_BC=false;
   GlobalParameters::ABC_order=2;
   break;
 
  case 3:
   GlobalParameters::DtN_BC=false;
   GlobalParameters::ABC_order=3;
   break;
  }

Next we build the problem, either with or without enabling spatial adaptivity and define the output directory.

 
 
 //Set up the problem
 //------------------
 
#ifdef ADAPTIVE
 
 //Set up the problem with 2D nine-node elements from the
 //QHelmholtzElement family.
 ScatteringProblem<RefineableQHelmholtzElement<2,3> > 
  problem;
 
#else
 
 //Set up the problem with 2D nine-node elements from the
 //QHelmholtzElement family. 
 ScatteringProblem<QHelmholtzElement<2,3> > 
  problem;
 
 
#endif
 
 // Create label for output
 //------------------------
 DocInfo doc_info;
 
 // Set output directory
 doc_info.set_directory("RESLT");

Finally, we solve the problem and document the results.

 
 
#ifdef ADAPTIVE
 
 // Max. number of adaptations
 unsigned max_adapt=1;
 
   // Solve the problem with Newton's method, allowing
   // up to max_adapt mesh adaptations after every solve.
   problem.newton_solve(max_adapt);
 
#else
 
   // Solve the problem with Newton's method
   problem.newton_solve();
 
#endif
 
 //Output solution
 problem.doc_solution(doc_info);
    
} //end of main

The problem class

The problem class is very similar to that employed for the adaptive solution of the 2D Poisson equation with flux boundary conditions. The only difference is that we provide two separate meshes of FaceElements: one for the inner boundary where the HelmholtzFluxElements apply the Neumann condition (9), and one for the outer boundary where we apply the (approximate) Sommerfeld radiation condition. As discussed in section The Dirichlet-to-Neumann mapping (DtN) , we use the function actions_before_newton_convergence_check() to recompute the $\gamma$ integral whenever the unknowns are updated during the Newton iteration.

//========= start_of_problem_class=====================================
/// Problem class to compute scattering of planar wave from unit disk
//=====================================================================
template<class ELEMENT> 
class ScatteringProblem : public Problem
{
 
public:
 
 /// Constructor
 ScatteringProblem();
 
 /// Destructor (empty)
 ~ScatteringProblem(){}
 
 /// Doc the solution. DocInfo object stores flags/labels for where the
 /// output gets written to
 void doc_solution(DocInfo& doc_info);
 
 /// Update the problem specs before solve (empty)
 void actions_before_newton_solve(){} 
 
 /// Update the problem specs after solve (empty)
 void actions_after_newton_solve(){}
 
 /// Recompute gamma integral before checking Newton residuals
 void actions_before_newton_convergence_check()
  {
   if (GlobalParameters::DtN_BC)
    {
     Helmholtz_outer_boundary_mesh_pt->setup_gamma();
    }
  }
 
 /// Actions before adapt: Wipe the mesh of prescribed flux elements
 void actions_before_adapt();
 
 /// Actions after adapt: Rebuild the mesh of prescribed flux elements
 void actions_after_adapt();
 
 /// Create BC elements on boundary b of the Mesh pointed
 /// to by bulk_mesh_pt and add them to the specified survace Mesh 
 void create_outer_bc_elements(
  const unsigned &b, Mesh* const &bulk_mesh_pt,
  Mesh* const & helmholtz_outer_boundary_mesh_pt);
 
 /// Create Helmholtz flux elements on boundary b of the Mesh pointed
 /// to by bulk_mesh_pt and add them to the specified surface Mesh 
 void create_flux_elements(const unsigned &b, Mesh* const &bulk_mesh_pt,
                           Mesh* const & helmholtz_inner_boundary_mesh_pt);
 
 /// Delete boundary face elements and wipe the surface mesh
 void delete_face_elements( Mesh* const & boundary_mesh_pt);
 
 /// Set pointer to prescribed-flux function for all
 /// elements in the surface mesh on the surface of the unit disk
 void set_prescribed_incoming_flux_pt();
 
 /// Set up boundary condition elements on outer boundary
 void setup_outer_boundary();
 
#ifdef ADAPTIVE
 
/// Pointer to the "bulk" mesh
 RefineableTwoDAnnularMesh<ELEMENT>* Bulk_mesh_pt;
 
#else
 
 /// Pointer to the "bulk" mesh
 TwoDAnnularMesh<ELEMENT>* Bulk_mesh_pt;
 
#endif
 
 /// Pointer to mesh containing the DtN (or ABC) boundary
 /// condition elements
 HelmholtzDtNMesh<ELEMENT>* Helmholtz_outer_boundary_mesh_pt;
 
 /// Pointer to the mesh containing 
 /// the Helmholtz inner boundary condition elements 
 Mesh* Helmholtz_inner_boundary_mesh_pt;
 
}; // end of problem class

The problem constructor

We start by building the bulk mesh, using the refineable or non-refineable version of the TwoDAnnularMesh, depending on the macro ADAPTIVE. (The error tolerances for the adaptive version are chosen such that the mesh is refined non-uniformly – with the default tolerances, oomph-lib's automatic mesh adaptation procedure refine the mesh uniformly.)

//=======start_of_constructor=============================================
/// Constructor for Helmholtz problem
//========================================================================
template<class ELEMENT>
ScatteringProblem<ELEMENT>::
ScatteringProblem()
{ 
 
 // Setup "bulk" mesh
 
 // # of elements in theta
 unsigned n_theta=15;
 
 // # of elements in radius
 unsigned n_r=5;
 
 // Inner radius
 double a=1.0;
 
 // Thickness of annular computational domain
 double h=0.5; 
 
 // Set outer radius
 GlobalParameters::Outer_radius=a+h;
 
 // Mesh is periodic
 bool periodic=true; 
 
 // Full circle
 double azimuthal_fraction=1.0;
 
#ifdef ADAPTIVE
 
 // Build "bulk" mesh
 Bulk_mesh_pt=
  new RefineableTwoDAnnularMesh<ELEMENT>(periodic,
                                         azimuthal_fraction,n_theta,n_r,a,h);
 
 // Create/set error estimator
 Bulk_mesh_pt->spatial_error_estimator_pt()=new Z2ErrorEstimator;
 
 // Choose error tolerances to force some uniform refinement
 Bulk_mesh_pt->min_permitted_error()=0.004;
 Bulk_mesh_pt->max_permitted_error()=0.01;
 
#else
 
 // Build "bulk" mesh
 Bulk_mesh_pt=
  new TwoDAnnularMesh<ELEMENT>(periodic,
                               azimuthal_fraction,n_theta,n_r,a,h);
 
#endif

Next we create the two (empty) meshes for the FaceElements,

 // Pointer to mesh containing the Helmholtz outer boundary condition
 // elements. Specify outer radius and number of Fourier terms to be
 // used in gamma integral
 Helmholtz_outer_boundary_mesh_pt = 
  new HelmholtzDtNMesh<ELEMENT>(a+h,GlobalParameters::N_fourier);
 
 // Pointer to mesh containing the Helmholtz inner boundary condition
 // elements. Specify outer radius
 Helmholtz_inner_boundary_mesh_pt = new Mesh;

and populate them using the functions create_flux_elements(...) and create_outer_bc_elements(...).

 // Create prescribed-flux elements from all elements that are 
 // adjacent to the inner boundary , but add them to a separate mesh.
 create_flux_elements(0,Bulk_mesh_pt,Helmholtz_inner_boundary_mesh_pt);
 
 // Create outer boundary elements from all elements that are 
 // adjacent to the outer boundary , but add them to a separate mesh.
 create_outer_bc_elements(2,Bulk_mesh_pt,Helmholtz_outer_boundary_mesh_pt);

We add the various (sub-)meshes to the problem and build the global mesh

 // Add the several  sub meshes to the problem
 add_sub_mesh(Bulk_mesh_pt);
 add_sub_mesh(Helmholtz_outer_boundary_mesh_pt); 
 add_sub_mesh(Helmholtz_inner_boundary_mesh_pt);   
  
 // Build the Problem's global mesh from its various sub-meshes
 build_global_mesh();

Finally, we complete the build of the various elements by by passing pointers to the relevant quantities to them, and assign the equation numbers.

 // Complete the build of all elements so they are fully functional
 
 // Loop over the Helmholtz bulk elements to set up element-specific 
 // things that cannot be handled by constructor: Pass pointer to 
 // wave number squared
 unsigned n_element = Bulk_mesh_pt->nelement();
 for(unsigned e=0;e<n_element;e++)
  {
   // Upcast from GeneralisedElement to Helmholtz bulk element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(Bulk_mesh_pt->element_pt(e));
   
   //Set the k_squared  pointer
   el_pt->k_squared_pt() = &GlobalParameters::K_squared;
  }
 
 // Set up elements on outer boundary
 setup_outer_boundary();
 
 // Set pointer to prescribed flux function for flux elements
 set_prescribed_incoming_flux_pt();
 
 // Setup equation numbering scheme
 cout <<"Number of equations: " << assign_eqn_numbers() << std::endl; 
 
} // end of constructor

The problem is now ready to be solved.

Actions before adapt

The mesh adaptation is driven by the error estimates for the bulk elements. The various FaceElements must therefore be removed from the global mesh before the adaptation takes place. We do this by calling the function delete_flux_elements(...) for the two face meshes, before rebuilding the Problem's global mesh.

//=====================start_of_actions_before_adapt======================
/// Actions before adapt: Wipe the mesh of face elements
//========================================================================
template<class ELEMENT>
void ScatteringProblem<ELEMENT>::actions_before_adapt()
{ 
 // Kill the flux elements and wipe the boundary meshs
 delete_face_elements(Helmholtz_outer_boundary_mesh_pt);
 delete_face_elements(Helmholtz_inner_boundary_mesh_pt);
 
 // Rebuild the Problem's global mesh from its various sub-meshes
 rebuild_global_mesh();
 
}// end of actions_before_adapt

Actions after adapt

After the (bulk-)mesh has been adapted, the flux elements must be re-attached. This is done by calling the functions create_flux_elements(...) and create_outer_bc_elements, followed by rebuilding the Problem's global mesh. Finally, we complete the build of the FaceElements by calling the functions setup_outer_boundary() and set_prescribed_incoming_flux_pt().

//=====================start_of_actions_after_adapt=======================
///  Actions after adapt: Rebuild the face element meshes
//========================================================================
template<class ELEMENT>
void ScatteringProblem<ELEMENT>::actions_after_adapt()
{
 // Create prescribed-flux elements and BC elements 
 // from all elements that are adjacent to the boundaries and add them to 
 // Helmholtz_boundary_meshes
 create_outer_bc_elements(2,Bulk_mesh_pt,Helmholtz_outer_boundary_mesh_pt);
 create_flux_elements(0,Bulk_mesh_pt,Helmholtz_inner_boundary_mesh_pt);
 
 // Rebuild the Problem's global mesh from its various sub-meshes
 rebuild_global_mesh();
 
 // Set pointer to prescribed flux function and DtN mesh
 setup_outer_boundary();
 set_prescribed_incoming_flux_pt(); 
  
}// end of actions_after_adapt

Delete flux elements

The helper function delete_face_elements() is used to delete all FaceElements in a given surface mesh before the mesh adaptation.

//============start_of_delete_face_elements================
/// Delete face elements and wipe the boundary mesh
//==========================================================
template<class ELEMENT>
void ScatteringProblem<ELEMENT>::
delete_face_elements(Mesh* const & boundary_mesh_pt)
{
 // Loop over the surface elements
 unsigned n_element = boundary_mesh_pt->nelement();
 for(unsigned e=0;e<n_element;e++)
  {
   // Kill surface element
   delete  boundary_mesh_pt->element_pt(e);
  }
 
 // Wipe the mesh
 boundary_mesh_pt->flush_element_and_node_storage();
 
} // end of delete_outer_face_elements

Creating the face elements

The functions create_flux_elements(...) and create_outer_bc_elements(...) create the FaceElements required to apply the boundary conditions on the inner and outer boundaries of the annular computational domain. They both loop over the bulk elements that are adjacent to the appropriate mesh boundary and attach the required FaceElements to their faces. The newly created FaceElements are then added to the appropriate mesh.

//============start_of_create_outer_bc_elements==============================
/// Create outer BC elements on the b-th boundary of 
/// the Mesh object pointed to by bulk_mesh_pt and add the elements 
/// to the Mesh object pointed to by helmholtz_outer_boundary_mesh_pt.
//===========================================================================
template<class ELEMENT>
void ScatteringProblem<ELEMENT>::
create_outer_bc_elements(const unsigned &b, Mesh* const &bulk_mesh_pt,
                         Mesh* const & helmholtz_outer_boundary_mesh_pt)
{
 // Loop over the bulk elements adjacent to boundary b?
 unsigned n_element = bulk_mesh_pt->nboundary_element(b);
 for(unsigned e=0;e<n_element;e++)
  {
   // Get pointer to the bulk element that is adjacent to boundary b
   ELEMENT* bulk_elem_pt = dynamic_cast<ELEMENT*>(
    bulk_mesh_pt->boundary_element_pt(b,e));
   
   //Find the index of the face of element e along boundary b 
   int face_index = bulk_mesh_pt->face_index_at_boundary(b,e);
   
   // Build the corresponding outer flux element
   
   // Dirichlet to Neumann boundary conditon
   if (GlobalParameters::DtN_BC)
    {
     HelmholtzDtNBoundaryElement<ELEMENT>* flux_element_pt = new 
      HelmholtzDtNBoundaryElement<ELEMENT>(bulk_elem_pt,face_index);
     
     //Add the flux boundary element to the  helmholtz_outer_boundary_mesh
     helmholtz_outer_boundary_mesh_pt->add_element_pt(flux_element_pt);
    }
   //  ABCs BC
   else
    {
     HelmholtzAbsorbingBCElement<ELEMENT>* flux_element_pt = new 
      HelmholtzAbsorbingBCElement<ELEMENT>(bulk_elem_pt,face_index);
     
     //Add the flux boundary element to the  helmholtz_outer_boundary_mesh
     helmholtz_outer_boundary_mesh_pt->add_element_pt(flux_element_pt);
    }
  } //end of loop over bulk elements adjacent to boundary b
} // end of create_outer_bc_elements

(We omit the listing of the function create_flux_elements(...) because it is very similar. Feel free to inspect in the source code.)

Post-processing

The post-processing function doc_solution(...) computes and outputs the total radiated power, and plots the computed and exact solutions (real and complex parts).

//=====================start_of_doc=======================================
/// Doc the solution: doc_info contains labels/output directory etc.
//========================================================================
template<class ELEMENT>
void ScatteringProblem<ELEMENT>::doc_solution(DocInfo& 
                                              doc_info) 
{ 
 
 ofstream some_file,some_file2;
 char filename[100];
 
 // Number of plot points
 unsigned npts;
 npts=5; 
 
 // Compute/output the radiated power
 //----------------------------------
 sprintf(filename,"%s/power%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 
 // Accumulate contribution from elements
 double power=0.0;
 unsigned nn_element=Helmholtz_outer_boundary_mesh_pt->nelement(); 
 for(unsigned e=0;e<nn_element;e++)
  {
   HelmholtzBCElementBase<ELEMENT> *el_pt = 
    dynamic_cast< HelmholtzBCElementBase<ELEMENT>*>(
     Helmholtz_outer_boundary_mesh_pt->element_pt(e)); 
   power += el_pt->global_power_contribution(some_file);
  }
 some_file.close();
 oomph_info << "Total radiated power: " << power << std::endl; 
 
 // Output solution 
 //-----------------
 sprintf(filename,"%s/soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Bulk_mesh_pt->output(some_file,npts);
 some_file.close();
 
  // Output exact solution 
 //----------------------
 sprintf(filename,"%s/exact_soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Bulk_mesh_pt->output_fct(some_file,npts,GlobalParameters::get_exact_u); 
 some_file.close();
 
 double error,norm;
 sprintf(filename,"%s/error%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Bulk_mesh_pt->compute_error(some_file,GlobalParameters::get_exact_u,
                             error,norm); 
 some_file.close();
 
 // Doc L2 error and norm of solution
 oomph_info << "\nNorm of error   : " << sqrt(error) << std::endl; 
 oomph_info << "Norm of solution: " << sqrt(norm) << std::endl << std::endl;

Finally, we create the data required to produce an animation of the actual (real) potential at 40 instants during a period of the oscillation.

 
 
 // Do animation of Helmholtz solution
 //-----------------------------------
 unsigned nstep=40;
 for (unsigned i=0;i<nstep;i++)
  {
   sprintf(filename,"%s/helmholtz_animation%i_frame%i.dat",
           doc_info.directory().c_str(),
           doc_info.number(),i);
   some_file.open(filename);
   sprintf(filename,"%s/exact_helmholtz_animation%i_frame%i.dat",
           doc_info.directory().c_str(),
           doc_info.number(),i);
   some_file2.open(filename);
   double phi=2.0*MathematicalConstants::Pi*double(i)/double(nstep-1);
   unsigned nelem=Bulk_mesh_pt->nelement();
   for (unsigned e=0;e<nelem;e++)
    {
     ELEMENT* el_pt=dynamic_cast<ELEMENT*>(
      Bulk_mesh_pt->element_pt(e));
     el_pt->output_real(some_file,phi,npts);    
     el_pt->output_real_fct(some_file2,phi,npts,
                            GlobalParameters::get_exact_u); 
    }
   some_file.close();
   some_file2.close();
  }
 
} // end of doc

Comments and Exercises

The enumeration of the unknowns

As discussed in the introduction, most practically relevant solutions of the Helmholtz equation are complex valued. Since oomph-lib's solvers only deal with real (double precision) unknowns, the equations are separated into their real and imaginary parts. In the implementation of the Helmholtz elements, we store the real and imaginary parts of the solution as two separate values at each node. By default, the real and imaginary parts are accessible via Node::value(0) and Node::value(1). However, to facilitate the use of the elements in multi-physics problems we avoid accessing the unknowns directly in this manner but provide the virtual function

std::complex<unsigned> HelmholtzEquations<DIM>::u_index_helmholtz()

which returns a complex number made of the two unsigneds that indicate which nodal value represents the real and imaginary parts of the solution. This function may be overloaded in combined multi-physics elements in which a Helmholtz element is combined (by multiple inheritance) with another element, using the strategy described in the Boussinesq convection tutorial.

Exercises

Exploiting linearity

Confirm that the (costly) re-computation of the $\gamma$ integral in actions_before_newton_convergence_check() after the first (and only) linear solve in the Newton iteration can be avoided by declaring the problem to be linear.

The accuracy of the boundary condition elements

Explore the accuracy (and computational cost) of the various FaceElements that apply the Sommmerfeld radiation condition. In particular, confirm that the accuracy of the DtN boundary condition is (nearly) independent of the radius of the artificial outer boundary, whereas the accuracy of the ABC boundary condition can only be improved by increasing the size of the computational domain.

Source files for this tutorial

The source files for this tutorial are located in the directory: demo_drivers/helmholtz/scattering/
The driver code is: demo_drivers/helmholtz/scattering/scattering.cc

PDF file

A pdf version of this document is available.