This tutorial demonstrates the use of unstructured meshes in 2D fluid-structure interaction problems. We combine two single-physics problems, namely

Large deformations of an elastic 2D solid, loaded by surface tractions and a gravitational body force
Flow through a 2D channel that is partly obstructed by a rigid 2D solid body

for which we have already created unstructured 2D meshes, using the combination of xfig, oomph-lib's conversion code fig2poly, and the unstructured mesh generator Triangle.

The problem

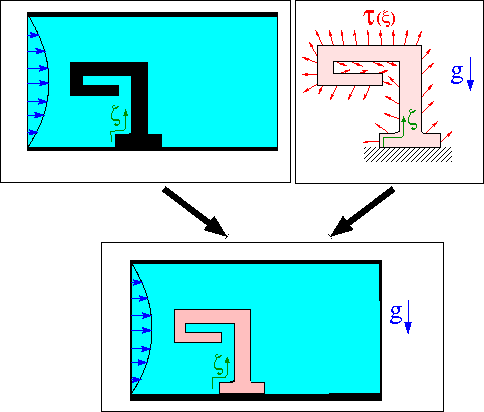
The figure below shows a sketch of the problem. A 2D channel is partly obstructed by an odd-shaped elastic obstacle that deforms in response to gravity and to the traction that the fluid exerts onto it. The coupled problem is a straightforward combination of the two single-physics problems shown at the top of the sketch: The flow through a channel with a rigid obstacle (shown on the top left), and the deformation of the elastic obstacle in response to a prescribed surface traction (shown on the top right). When the two constituent single-physics problems interact, the fluid provides the traction onto the solid while the change in the solid's shape affects the fluid domain.

Sketch of the problem and its two single-physics constituents.

As usual, we solve the problem in non-dimensional form. For this purpose we non-dimensionalise all lengths on some reference length ${\cal L}$ and use the average inflow velocity, ${\cal U}$ , to non-dimensionalise the velocities in the Navier-Stokes equations. As discussed in the single-physics fluids tutorial, the Reynolds number of the flow is then given by

$Re = \frac{\rho {\cal U} {\cal L}}{\mu} \ ,$

where $\rho$ and $\mu$ are the fluid density and viscosity, respectively. oomph-lib's Navier Stokes elements non-dimensionalise the fluid stresses, and in particular the pressure, on the viscous scale, $\mu {\cal U}/{\cal L}$ .

We assume that the solid's constitutive equation is given by oomph-lib's generalised Hookean constitutive law and non-dimensionalise the solid-mechanics stresses and tractions with Young's modulus .

The FSI interaction parameter which represents the ratio of the (viscous) fluid stress scale to the reference stress used to non-dimensionalise the solid stresses is therefore given by

$Q = \frac{\mu {\cal U}}{{\cal L} E} \ .$

Results

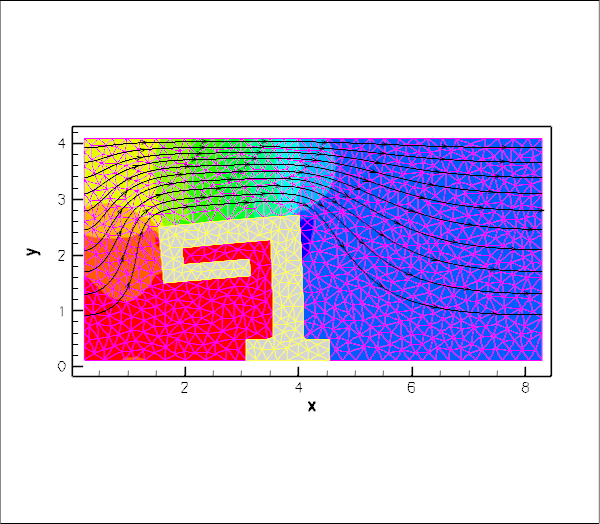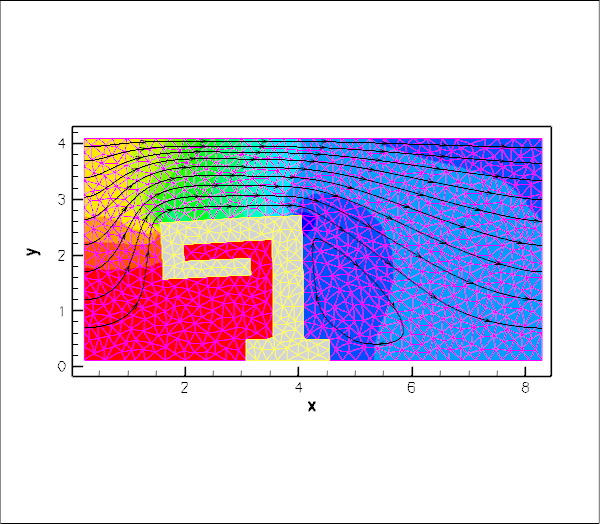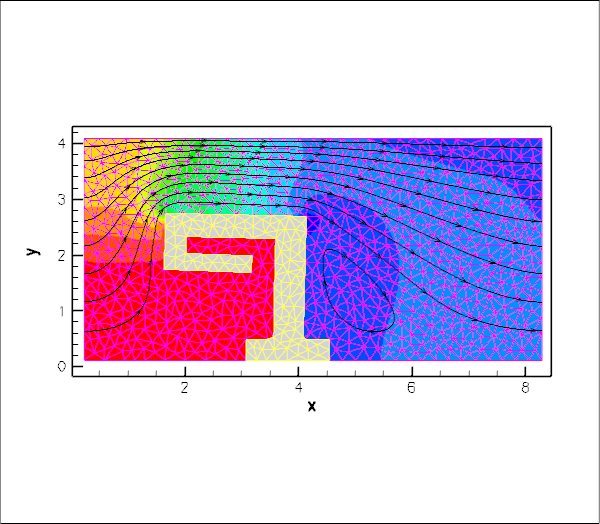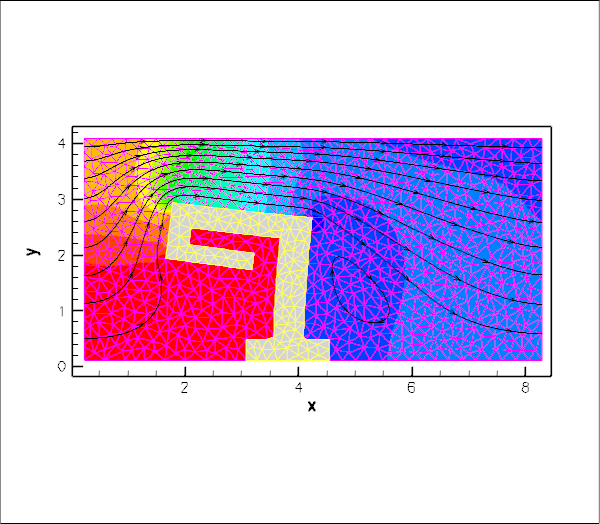
The animation below shows a number of steady flow fields (streamlines and pressure contours) and deformations, obtained in a parameter study in which we first compute the solution of the coupled problem at zero Reynolds number and for a vanishing FSI interaction parameter, . For these parameter values, the structure is loaded only by gravity and does not feel the presence of the fluid, whereas the fluid flow is affected by the changes to the fluid domain when the obstacle deforms (first frame). Next, we increase the Reynolds number to and re-compute the solution (second frame), before increasing in small increments (subsequent frames). The increase in may be interpreted as a reduction in the obstacle's stiffness and the animation shows clearly how this increases its flow-induced deformation.

Animation of the flow field (streamlines and pressure contours) and the deformation of the elastic obstacle.

Overview of the implementation

The use of unstructured meshes means that the design of an algebraic node update strategy for the deforming fluid mesh, as described for fluid-structure interaction with structured meshes, is (almost) impossible and would, in any case, defeat the point of using automatic mesh generation tools. A slightly less efficient, but easily and generally applicable strategy is to update the nodal positions within the fluid mesh by treating the fluid domain as a pseudo-elastic solid. Apart from this change in the node-update strategy, the majority of the steps described below are the same as for fluid-structure-interaction problems on structured meshes.

One important prerequisite for the use of the FSI helper functions in oomph-lib's FSI_functions namespace is that each boundary at the FSI interface between the fluid and solid meshes must be parametrised by boundary coordinates. Moreover, the boundary-coordinate representations in the fluid and solid meshes must be consistent. Once the appropriate boundaries have been identified, oomph-lib's unstructured meshes allow the automatic (and consistent) generation of these boundary coordinates; see How the boundary coordinates are generated. Unfortunately, different third-party mesh generators use different strategies to label mesh boundaries and a certain amount of "manual labour" tends be required to identify boundaries after the mesh has been imported into oomph-lib.

Since the driver code, discussed in detail below, is somewhat lengthy (partly because of the large number of self-tests and diagnostics included), we provide a brief overview of the main steps required to solve this problem:

Use the combination of xfig, oomph-lib's conversion code fig2poly, and the unstructured mesh generator Triangle to generate the solid mesh, as already discussed in another tutorial.
Use the same procedure to generate the fluid mesh, as discussed in the single-physics fluids tutorial. Make sure that the fluid mesh is derived from the SolidMesh base class to allow the use of pseudo-elasticity to update the nodal positions in response to the deformation of the domain boundary.
Ensure that boundary coordinates are set up (consistently) on the FSI interface between the two meshes. For meshes derived from oomph-lib's TriangleMesh class, this may be done by calling the function TriangleMesh::setup_boundary_coordinates().
Attach FSISolidTractionElements to the faces of the "bulk" solid elements that are exposed to the fluid flow. These elements will apply the fluid traction to the solid.
Combine the FSISolidTractionElements into a compound GeomObject that provides a continuous representation of the solid's FSI boundary, required by the ImposeDisplacementByLagrangeMultiplierElements described below.
Attach ImposeDisplacementByLagrangeMultiplierElements to the faces of the "bulk" fluid elements that are adjacent to the solid. These elements will employ Lagrange multipliers to deform the pseudo-solid fluid mesh so that its shape remains consistent with the solid's FSI boundary (as described by the compound GeomObject created in the previous step).
Determine the "bulk" fluid elements that are adjacent to the integration points of the FSISolidTractionElements, using the function FSI_functions::setup_fluid_load_info_for_solid_elements(...).

In our experience, the most error-prone part of this procedure is the identification of the mesh boundaries in the xfig-based, unstructured meshes. It is very easy to exclude a node at the end of the FSI boundary in the fluid mesh, say, while "remembering" it in the solid mesh. If this happens, the automatic matching of the unstructured fluid and solid meshes will not work (see How the boundary coordinates are generated for details). For this reason, the driver code presented below generates a lot of output that can be used to identify and fix such problems. See also the section What can go wrong? at the end of this tutorial.

Problem Parameters

As usual we define the various problem parameters in a global namespace. We define the Reynolds number, , and the FSI interaction parameter .

//==start_of_namespace==============================
/// Namespace for physical parameters
//==================================================
namespace Global_Parameters
{
 /// Reynolds number
 double Re=0.0; 
 
 /// FSI parameter
 double Q=0.0;

We define the gravitational body force that acts (only!) on the solid
(see Gravity only affects the solid – really? to find out why this is odd...)

 
 /// Non-dim gravity
 double Gravity=0.0;
 
 /// Non-dimensional gravity as body force
 void gravity(const double& time, 
              const Vector<double> &xi, 
              Vector<double> &b)
 {
  b[0]=0.0;
  b[1]=-Gravity;
 }

and provide a pointer to the constitutive equation for the solid. For simplicity, this constitutive equation will also be used for the (pseudo-)solid elements that determine the deformation of the fluid mesh. In general, the constitutive law used to control the deformation of the fluid mesh need not have any physical basis, it is more important that the elements do not become too deformed during the mesh motion.

 
 /// Pseudo-solid Poisson ratio
 double Nu=0.3;
 
 /// Constitutive law for the solid (and pseudo-solid) mechanics
 ConstitutiveLaw *Constitutive_law_pt=0;

Finally, we provide a helper function that will be used to establish whether a node is located on the FSI boundary when the mesh is in its undeformed configuration. This function uses a simple "brute force" approach. It is required because currently our xfig-based mesh generation procedures do not allow us to associate fractional parts of a polygonal domain boundary as belonging to different mesh boundaries. Hence, such boundaries have to be identified a posteriori in the driver code. Although similar in form, equivalent helper functions must be (re-)written for different domain geometries.

 
 /// Boolean to identify if node is on fsi boundary
 bool is_on_fsi_boundary(Node* nod_pt)
 {
  if (
   (
    // Is it a boundary node?
    dynamic_cast<BoundaryNodeBase*>(nod_pt)!=0)&&
   (
    // Horizontal extent of main immersed obstacle
    (  (nod_pt->x(0)>1.6)&&(nod_pt->x(0)<4.75)&&
       // Vertical extent of main immersed obstacle
       (nod_pt->x(1)>0.1125)&&(nod_pt->x(1)<2.8) ) ||
    // Two nodes on the bottom wall are below y=0.3
    (  (nod_pt->x(1)<0.3)&&
       // ...and bracketed in these two x-ranges
       (  ( (nod_pt->x(0)>3.0)&&(nod_pt->x(0)<3.1) ) ||
          ( (nod_pt->x(0)<4.6)&&(nod_pt->x(0)>4.5) )   ) 
     )
    )
   )
   {
    return true;
   }
  else
   {
    return false;
   }
 }
 
 
} // end_of_namespace

Creating the meshes

The solid mesh

Following the procedure discussed in the corresponding single-physics solid mechanics problem we create the mesh for the elastic obstacle using multiple inheritance from oomph-lib's TriangleMesh and the SolidMesh base class.

//========start_solid_mesh=================================================
/// Triangle-based mesh upgraded to become a solid mesh
//=========================================================================
template<class ELEMENT>
class MySolidTriangleMesh : public virtual TriangleMesh<ELEMENT>, 
                          public virtual SolidMesh 
{

As before, we set the Lagrangian coordinates to the current nodal positions to make the initial configuration stress-free. Initially all boundary nodes are located on the same boundary, corresponding to the single xfig polyline that defines the surface of the elastic obstacle. In the current problem we have to identify two additional boundaries: The "bottom boundary" (boundary 1) where the positions of the solid nodes will be pinned; and the nodes that are located on the FSI boundary (boundary 2).

 
public:
 
 /// Constructor: 
 MySolidTriangleMesh(const std::string& node_file_name,
                     const std::string& element_file_name,
                     const std::string& poly_file_name,
                     TimeStepper* time_stepper_pt=
                     &Mesh::Default_TimeStepper) :
  TriangleMesh<ELEMENT>(node_file_name,element_file_name,
                        poly_file_name, time_stepper_pt)
  {
   //Assign the Lagrangian coordinates
   set_lagrangian_nodal_coordinates();
 
   // Identify special boundaries
   set_nboundary(3);
 
   unsigned n_node=this->nnode();
   for (unsigned j=0;j<n_node;j++)
    {
     Node* nod_pt=this->node_pt(j);
 
     // Boundary 1 is lower boundary
     if (nod_pt->x(1)<0.15)
      {
       this->remove_boundary_node(0,nod_pt);
       this->add_boundary_node(1,nod_pt);
      }
 
     // Boundary 2 is FSI interface
     if (Global_Parameters::is_on_fsi_boundary(nod_pt))
      {
       this->remove_boundary_node(0,nod_pt);
       this->add_boundary_node(2,nod_pt);
      }
    }// done boundary assignment

Finally, we identify the elements that are located next to the newly created domain boundaries and create boundary coordinates along boundaries 1 and 2.

 
   // Identify the elements next to the newly created boundaries
   TriangleMesh<ELEMENT>::setup_boundary_element_info();
   
   // Setup boundary coordinates for boundaries 1 and 2
   this->template setup_boundary_coordinates<ELEMENT>(1);
   this->template setup_boundary_coordinates<ELEMENT>(2);
  }
 
 /// Empty Destructor
 virtual ~MySolidTriangleMesh() { }
 
};

The fluid mesh

The creation of the fluid mesh follows the same process but uses the mesh created for the
single-physics fluids problem. The use of multiple inheritance from the TriangleMesh and SolidMesh base classes will allow us to employ pseudo-solid node-update techniques to update the position of the fluid nodes in response to changes in the domain boundary.

//======================start_fluid_mesh===================================
/// Triangle-based mesh upgraded to become a pseudo-solid mesh
//=========================================================================
template<class ELEMENT>
class FluidTriangleMesh : public virtual TriangleMesh<ELEMENT>,
                          public virtual SolidMesh 
{
 
public:
 
 /// Constructor
 FluidTriangleMesh(const std::string& node_file_name,
                   const std::string& element_file_name,
                   const std::string& poly_file_name,
                   TimeStepper* time_stepper_pt=
                   &Mesh::Default_TimeStepper) :
  TriangleMesh<ELEMENT>(node_file_name,element_file_name,
                        poly_file_name, time_stepper_pt)
  {
   //Assign the Lagrangian coordinates
   set_lagrangian_nodal_coordinates();

The fluid problem requires the identification of three additional boundaries: The inflow boundary (boundary 1), the outflow boundary (boundary 2) and the FSI boundary (boundary 3).

 
   // Identify special boundaries
   this->set_nboundary(4);
 
   unsigned n_node=this->nnode();
   for (unsigned j=0;j<n_node;j++)
    {
     Node* nod_pt=this->node_pt(j);
 
     // Boundary 1 is left (inflow) boundary
     if (nod_pt->x(0)<0.226)
      {
       this->remove_boundary_node(0,nod_pt);
       this->add_boundary_node(1,nod_pt);
 
       // Add overlapping nodes back to boundary 0
       if (nod_pt->x(1)<0.2) this->add_boundary_node(0,nod_pt);
       if (nod_pt->x(1)>4.06) this->add_boundary_node(0,nod_pt);
      }
 
     // Boundary 2 is right (outflow) boundary
     if (nod_pt->x(0)>8.28)
      {
       this->remove_boundary_node(0,nod_pt);
       this->add_boundary_node(2,nod_pt);
 
       // Add overlapping nodes back to boundary 0
       if (nod_pt->x(1)<0.2) this->add_boundary_node(0,nod_pt);
       if (nod_pt->x(1)>4.06) this->add_boundary_node(0,nod_pt);
 
      }
 
     // Boundary 3 is FSI boundary
     if (Global_Parameters::is_on_fsi_boundary(nod_pt))
      {
       this->remove_boundary_node(0,nod_pt);
       this->add_boundary_node(3,nod_pt);
       
       //If it's below y=0.2 it's also on boundary 0 so stick it back on
       if (nod_pt->x(1)<0.2) this->add_boundary_node(0,nod_pt);
      }
    }
   TriangleMesh<ELEMENT>::setup_boundary_element_info();

We create boundary coordinates along the three newly-created mesh boundaries and document the process for the FSI boundary (boundary 3). See What can go wrong? for a more detailed discussion of the output created here.

   
   // Open a file to doc the FaceElements that are used to
   // create the boundary coordinates. The elements must
   // form a simply-connected line. This may not work
   // if the mesh is too coarse so that, e.g. an element
   // that goes through the interior has endpoints that are
   // both located on the same boundary. Outputting the
   // FaceElements can help identify such cases.
   ofstream some_file("RESLT/boundary_generation_test.dat");
   
   // Setup boundary coordinates for boundaries 1, 2 and 3
   this->template setup_boundary_coordinates<ELEMENT>(1);
   this->template setup_boundary_coordinates<ELEMENT>(2);
   this->template setup_boundary_coordinates<ELEMENT>(3,some_file);
 
   // Close it again
   some_file.close();
  }
 
 /// Empty Destructor
 virtual ~FluidTriangleMesh() { }
 
};

The driver code

We specify an output directory and instantiate the constitutive equation for the solid mechanics computations, specifying the Poisson ratio. (Recall that the omission of Young's modulus in the constructor of the constitutive equation implies that all stresses and tractions are non-dimensionalised on .)

//==start_of_main======================================================
/// Driver for unstructured fsi problem
//=====================================================================
int main()
{
 // Label for output
 DocInfo doc_info;
 
 // Set output directory
 doc_info.set_directory("RESLT");
 
 //Create the constitutive law
 Global_Parameters::Constitutive_law_pt = new GeneralisedHookean(
  &Global_Parameters::Nu);

We create the Problem object and output the domain boundaries and the initial guess for the solution.

 
 // Build the problem with triangular Taylor Hood for fluid and solid
 UnstructuredFSIProblem<
 PseudoSolidNodeUpdateElement<TTaylorHoodElement<2>, TPVDElement<2,3> >, 
  TPVDElement<2,3> > problem;
 
 // Output boundaries 
 problem.fluid_mesh_pt()->output_boundaries("RESLT/fluid_boundaries.dat");
 problem.solid_mesh_pt()->output_boundaries("RESLT/solid_boundaries.dat");
 
 // Output the initial guess for the solution
 problem.doc_solution(doc_info);
 doc_info.number()++;

Finally, we perform a two-stage parameter study. We start by solving the problem at zero Reynolds number with the FSI parameter set to zero.

 
 // Parameter study
 Global_Parameters::Gravity=2.0e-4;
 double q_increment=1.0e-6;
 
 // Solve the problem at zero Re and Q
 problem.newton_solve();
 
 // Output the solution
 problem.doc_solution(doc_info);
 doc_info.number()++;

Next we re-solve the problem at finite Reynolds number, before slowly increasing the strength of the fluid-structure interaction.

 
 // Bump up Re
 Global_Parameters::Re=10.0;
 
 // Now do proper parameter study with increase in Q
 unsigned nstep=2; // 10;
 for (unsigned i=0;i<nstep;i++)
  {
   // Solve the problem
   problem.newton_solve();
   
   // Output the solution
   problem.doc_solution(doc_info);
   doc_info.number()++;
 
   // Bump up Q
   Global_Parameters::Q+=q_increment;
  }
 
 
} // end_of_main

The Problem class

The Problem class has the usual members, with access functions to the fluid and solid meshes, and a post-processing routine.

//==start_of_problem_class============================================
/// Unstructured FSI Problem
//====================================================================
template<class FLUID_ELEMENT, class SOLID_ELEMENT>
class UnstructuredFSIProblem : public Problem
{
 
public:
 
 /// Constructor
 UnstructuredFSIProblem();
 
 /// Destructor (empty)
 ~UnstructuredFSIProblem(){}
 
 /// Access function for the fluid mesh
 FluidTriangleMesh<FLUID_ELEMENT>*& fluid_mesh_pt() 
  {
   return Fluid_mesh_pt;
  }
 
 /// Access function for the solid mesh
 MySolidTriangleMesh<SOLID_ELEMENT>*& solid_mesh_pt() 
  {
   return Solid_mesh_pt;
  }
 
 /// Doc the solution
 void doc_solution(DocInfo& doc_info);

The class provides two private helper functions: one to create the FaceElements that apply the fluid traction to the solid and one to create the FaceElements that use Lagrange multipliers to deform the fluid mesh according to the motion of the solid boundary.

 
private:
 
 /// Create FSI traction elements
 void create_fsi_traction_elements();
 
 /// Create elements that enforce prescribed boundary motion
 /// for the pseudo-solid fluid mesh by Lagrange multipliers
 void create_lagrange_multiplier_elements();

Another private helper function is provided to document the boundary parametrisation of the solid's FSI interface:

 
 /// Sanity check: Doc boundary coordinates from solid side
 void doc_solid_boundary_coordinates();

The private member data includes pointers to the various meshes and a GeomObject representation of the FSI boundary.

 
 /// Fluid mesh
 FluidTriangleMesh<FLUID_ELEMENT>* Fluid_mesh_pt;
 
 /// Solid mesh
 MySolidTriangleMesh<SOLID_ELEMENT>* Solid_mesh_pt;
 
 /// Pointers to mesh of Lagrange multiplier elements
 SolidMesh* Lagrange_multiplier_mesh_pt;
 
 /// Vector of pointers to mesh of FSI traction elements
 SolidMesh* Traction_mesh_pt;
 
 /// GeomObject incarnation of fsi boundary in solid mesh
 MeshAsGeomObject* 
 Solid_fsi_boundary_pt;
 
}; 

The Problem constructor

We start by building the fluid mesh, using the files created by Triangle ; see the discussion in the corresponding single-physics fluids problem.

//==start_of_constructor==================================================
/// Constructor for unstructured FSI problem.
//========================================================================
template<class FLUID_ELEMENT, class SOLID_ELEMENT>
UnstructuredFSIProblem<FLUID_ELEMENT,SOLID_ELEMENT>::UnstructuredFSIProblem()
{ 
 
 // Fluid mesh
 //-----------
 
 //Create fluid mesh
 string fluid_node_file_name="fluid.fig.1.node";
 string fluid_element_file_name="fluid.fig.1.ele";
 string fluid_poly_file_name="fluid.fig.1.poly"; 
 Fluid_mesh_pt = new FluidTriangleMesh<FLUID_ELEMENT>(fluid_node_file_name,
                                                      fluid_element_file_name,
                                                      fluid_poly_file_name);

Next, we apply the boundary conditions for the fluid and the pseudo-solid equations. We pin the pseudo-solid nodes along all domain boundaries, apart from the FSI boundary (boundary 3), apply a no-slip condition for the fluid velocity along the solid channel walls (boundary 0) and the FSI boundary (boundary 3); pin the velocity at the inflow (boundary 1, where we will impose a Poiseuille flow profile); and impose parallel outflow at the downstream end (boundary 2). As mentioned before, the manual identification of mesh boundaries in unstructured meshes that are generated by third-party mesh generators is a relatively error-prone process. Therefore we document the boundary conditions for the pseudo-solid to allow an external sanity check.

 
 // Doc pinned solid nodes
 std::ofstream pseudo_solid_bc_file("pinned_pseudo_solid_nodes.dat");
 
 // Set the boundary conditions for fluid problem: All nodes are
 // free by default -- just pin the ones that have Dirichlet conditions
 // here. 
 unsigned nbound=Fluid_mesh_pt->nboundary();
 for(unsigned ibound=0;ibound<nbound;ibound++)
  {
   unsigned num_nod=Fluid_mesh_pt->nboundary_node(ibound);
   for (unsigned inod=0;inod<num_nod;inod++)
    {
     // Pin velocity everywhere apart from outlet where we
     // have parallel outflow
     if (ibound!=2)
      {
       Fluid_mesh_pt->boundary_node_pt(ibound,inod)->pin(0); 
      }
     Fluid_mesh_pt->boundary_node_pt(ibound,inod)->pin(1); 
 
     // Pin pseudo-solid positions everywhere apart from boundary 3, 
     // the fsi boundary 
     if ((ibound==0)||(ibound==1)||(ibound==2))
      {
       for(unsigned i=0;i<2;i++)
        {
         // Pin the node
         SolidNode* nod_pt=Fluid_mesh_pt->boundary_node_pt(ibound,inod);
         nod_pt->pin_position(i);
 
         // Doc it as pinned
         pseudo_solid_bc_file << nod_pt->x(i) << " ";
        }
       pseudo_solid_bc_file << std::endl;
      }
    }
  } // end loop over boundaries
 
 // Close
 pseudo_solid_bc_file.close();

We complete the build of the elements by specifying the Reynolds number and the constitutive equation used in the pseudo-solid mesh deformation.

 
 
 // Complete the build of the fluid elements so they are fully functional
 unsigned n_element = Fluid_mesh_pt->nelement();
 for(unsigned e=0;e<n_element;e++)
  {
   // Upcast from GeneralisedElement to the present element
   FLUID_ELEMENT* el_pt = 
    dynamic_cast<FLUID_ELEMENT*>(Fluid_mesh_pt->element_pt(e));
   
   //Set the Reynolds number
   el_pt->re_pt() = &Global_Parameters::Re;
   
   // Set the constitutive law for pseudo-elastic mesh deformation
   el_pt->constitutive_law_pt() =
    Global_Parameters::Constitutive_law_pt;
   
  } // end loop over elements

Finally, we impose a Poiseuille profile at the inflow boundary (boundary 1) and assign the equation numbers.

 
 
 // Apply fluid boundary conditions: Poiseuille at inflow
 
 // Find max. and min y-coordinate at inflow
 unsigned ibound=1;
 //Initialise both to the y-coordinate of the first boundary node
 double y_min=fluid_mesh_pt()->boundary_node_pt(ibound,0)->x(1);;
 double y_max=y_min;
 
 //Loop over the rest of the boundary nodes
 unsigned num_nod= fluid_mesh_pt()->nboundary_node(ibound);
 for (unsigned inod=1;inod<num_nod;inod++)
  {
   double y=fluid_mesh_pt()->boundary_node_pt(ibound,inod)->x(1);
   if (y>y_max)
    {
     y_max=y;
    }
   if (y<y_min)
    {
     y_min=y;
    }
  }
 double y_mid=0.5*(y_min+y_max);
 
 // Loop over all boundaries
 const unsigned n_boundary = fluid_mesh_pt()->nboundary();
 for (unsigned ibound=0;ibound<n_boundary;ibound++)
  {
   const unsigned num_nod= fluid_mesh_pt()->nboundary_node(ibound);
   for (unsigned inod=0;inod<num_nod;inod++)
    {
     // Parabolic inflow at the left boundary (boundary 1)
     if (ibound==1)
      {
       double y=fluid_mesh_pt()->boundary_node_pt(ibound,inod)->x(1);
       double veloc=1.5/(y_max-y_min)*
        (y-y_min)*(y_max-y)/((y_mid-y_min)*(y_max-y_mid));
       fluid_mesh_pt()->boundary_node_pt(ibound,inod)->set_value(0,veloc);
       fluid_mesh_pt()->boundary_node_pt(ibound,inod)->set_value(1,0.0);
      }
     // Zero flow elsewhere 
     else
      {
       fluid_mesh_pt()->boundary_node_pt(ibound,inod)->set_value(0,0.0);
       fluid_mesh_pt()->boundary_node_pt(ibound,inod)->set_value(1,0.0);
      }
    }
  } // end Poiseuille

Next, we create the solid mesh, using the files created by Triangle ; see the discussion in the corresponding single-physics solids problem.

 
 
 // Solid mesh
 //-----------
 
 //Create solid mesh
 string solid_node_file_name="solid.fig.1.node";
 string solid_element_file_name="solid.fig.1.ele";
 string solid_poly_file_name="solid.fig.1.poly"; 
 Solid_mesh_pt = new MySolidTriangleMesh<SOLID_ELEMENT>(solid_node_file_name,
                                                     solid_element_file_name,
                                                     solid_poly_file_name);

We complete the build of the solid elements by passing the pointer to the constitutive equation and the function pointer to the gravitational body force.

 
 
 // Complete the build of all solid elements so they are fully functional
 n_element = Solid_mesh_pt->nelement();
 for(unsigned i=0;i<n_element;i++)
  {
   //Cast to a solid element
   SOLID_ELEMENT *el_pt = 
    dynamic_cast<SOLID_ELEMENT*>(Solid_mesh_pt->element_pt(i));
 
   // Set the constitutive law
   el_pt->constitutive_law_pt() =
    Global_Parameters::Constitutive_law_pt;
   
   //Set the body force
   el_pt->body_force_fct_pt() = Global_Parameters::gravity;
  }

We suppress the displacements of the nodes on boundary 1.

 
 // Pin both positions at lower boundary of solid mesh (boundary 1)
 ibound=1;
 num_nod=Solid_mesh_pt->nboundary_node(ibound);
 for (unsigned inod=0;inod<num_nod;inod++)
  {    
   Solid_mesh_pt->boundary_node_pt(ibound,inod)->pin_position(0);
   Solid_mesh_pt->boundary_node_pt(ibound,inod)->pin_position(1);
  }

Next, we create the FaceElements that apply the fluid traction to the solid

 
 
 // Create FSI Traction elements
 //-----------------------------
 
 // Now construct the (empty) traction element mesh
 Traction_mesh_pt=new SolidMesh;
 
  // Build the FSI traction elements and add them to the traction mesh
 create_fsi_traction_elements();

and the FaceElements that use Lagrange multipliers to deform the fluid mesh to keep it aligned with the FSI boundary.

 
 // Create Lagrange multiplier mesh for boundary motion
 //----------------------------------------------------
 
 // Construct the mesh of elements that enforce prescribed boundary motion
 // of pseudo-solid fluid mesh by Lagrange multipliers
 Lagrange_multiplier_mesh_pt=new SolidMesh;
 create_lagrange_multiplier_elements();

We combine the various sub-meshes into a global mesh.

 
 
 // Combine meshes
 //---------------
 
 // Add sub meshes
 add_sub_mesh(Fluid_mesh_pt);
 add_sub_mesh(Solid_mesh_pt);
 add_sub_mesh(Traction_mesh_pt);
 add_sub_mesh(Lagrange_multiplier_mesh_pt);
 
 // Build global mesh
 build_global_mesh();

Finally, we set up the fluid-structure interaction by determining which "bulk" fluid elements are located next to the FSI traction elements that apply the fluid load to the solid. We document the boundary coordinate along the FSI interface by opening the Multi_domain_functions::Doc_boundary_coordinate_file stream before calling FSI_functions::setup_fluid_load_info_for_solid_elements(...) If this stream is open, the setup routine writes the Eulerian coordinates of the points on the FSI interface and their intrinsic surface coordinate $[ x, y, \zeta ]$ to the specified file.

 
 
 // Setup FSI
 //----------
 
 // Document the boundary coordinate  along the FSI interface 
 // of the fluid mesh during call to
 // setup_fluid_load_info_for_solid_elements()
 Multi_domain_functions::Doc_boundary_coordinate_file.open(
  "fluid_boundary_test.dat");
 
 // Work out which fluid dofs affect the residuals of the wall elements:
 // We pass the boundary between the fluid and solid meshes and 
 // pointers to the meshes. The interaction boundary is boundary 3
 // of the 2D fluid mesh.
 FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
  (this,3,Fluid_mesh_pt,Traction_mesh_pt);
 
 // Close the doc file
 Multi_domain_functions::Doc_boundary_coordinate_file.close();

We use the private helper function doc_solid_boundary_coordinates() to create the same output from the "solid side" of the FSI interface. This is useful for debugging purposes because it allows us to check whether the fluid and solid meshes employ a matching parametrisation of the FSI interface; see What can go wrong? for more details.

 
 // Sanity check: Doc boundary coordinates from solid side
 doc_solid_boundary_coordinates();

All that's left to do is to set up the equation numbering scheme and the problem is ready to be solved.

 
 // Setup equation numbering scheme
 cout <<"Number of equations: " << assign_eqn_numbers() << std::endl; 
 
} // end_of_constructor

Creating the FSI traction elements

The creation of the FSI traction elements adjacent to the solid boundary 2 follows the usual procedure. We loop over the relevant 2D "bulk" solid elements and attach the FSISolidTractionElements to the appropriate faces.

//============start_of_create_traction_elements==========================
/// Create FSI traction elements 
//=======================================================================
template<class FLUID_ELEMENT,class SOLID_ELEMENT>
void UnstructuredFSIProblem<FLUID_ELEMENT,SOLID_ELEMENT>::
create_fsi_traction_elements()
{
 // Traction elements are located on boundary 2 of solid bulk mesh
 unsigned b=2;
 
 // How many bulk elements are adjacent to boundary b?
 unsigned n_element = solid_mesh_pt()->nboundary_element(b);
 
 // Loop over the bulk elements adjacent to boundary b
 for(unsigned e=0;e<n_element;e++)
  {
   // Get pointer to the bulk element that is adjacent to boundary b
   SOLID_ELEMENT* bulk_elem_pt = dynamic_cast<SOLID_ELEMENT*>(
    solid_mesh_pt()->boundary_element_pt(b,e));
   
   //What is the index of the face of the element e along boundary b
   int face_index = solid_mesh_pt()->face_index_at_boundary(b,e);
  
   // Create new element 
   FSISolidTractionElement<SOLID_ELEMENT,2>* el_pt=
    new FSISolidTractionElement<SOLID_ELEMENT,2>(bulk_elem_pt,face_index);

Next we add the newly-created FaceElement to the mesh of traction elements, specify which boundary of the bulk mesh it is attached to, and pass the FSI interaction parameter to the element.

   
   // Add it to the mesh
   Traction_mesh_pt->add_element_pt(el_pt);
   
   // Specify boundary number
   el_pt->set_boundary_number_in_bulk_mesh(b);
   
   // Function that specifies the load ratios
   el_pt->q_pt() = &Global_Parameters::Q; 
  } 
 
 } // end of create_traction_elements

Creating the Lagrange multiplier elements

The creation of the FaceElements that use Lagrange multipliers to impose the boundary displacement of the pseudo-solid fluid mesh is again fairly straightforward (the use of Lagrange multipliers for the imposition of boundary displacements is explained in another tutorial). We start by combining the FSISolidTractionElements attached to the solid's FSI boundary to form a compound GeomObject. This GeomObject provides a continuous representation of the FSI boundary (as determined by the deformation of the solid) and is parametrised by the boundary coordinate assigned earlier. This continuous representation will define the desired position of the boundary as enforced by the Lagrange multiplier elements.

 
 
 
//============start_of_create_lagrange_multiplier_elements===============
/// Create elements that impose the prescribed boundary displacement
/// for the pseudo-solid fluid mesh
//=======================================================================
template<class FLUID_ELEMENT, class SOLID_ELEMENT>
void UnstructuredFSIProblem<FLUID_ELEMENT,SOLID_ELEMENT>::
create_lagrange_multiplier_elements()
{
 
 // Create  GeomObject incarnation of fsi boundary in solid mesh
 Solid_fsi_boundary_pt=
  new MeshAsGeomObject
  (Traction_mesh_pt);

Now we attach ImposeDisplacementByLagrangeMultiplierElements to the appropriate faces of the "bulk" fluid elements that are adjacent to the FSI interface (boundary 3 in the fluid mesh).

 
 // Lagrange multiplier elements are located on boundary 3 of the fluid mesh
 unsigned b=3;
 
 // How many bulk fluid elements are adjacent to boundary b?
 unsigned n_element = Fluid_mesh_pt->nboundary_element(b);
 
 // Loop over the bulk fluid elements adjacent to boundary b?
 for(unsigned e=0;e<n_element;e++)
  {
   // Get pointer to the bulk fluid element that is adjacent to boundary b
   FLUID_ELEMENT* bulk_elem_pt = dynamic_cast<FLUID_ELEMENT*>(
    Fluid_mesh_pt->boundary_element_pt(b,e));
   
   //Find the index of the face of element e along boundary b
   int face_index = Fluid_mesh_pt->face_index_at_boundary(b,e);
      
   // Create new element
   ImposeDisplacementByLagrangeMultiplierElement<FLUID_ELEMENT>* el_pt =
    new ImposeDisplacementByLagrangeMultiplierElement<FLUID_ELEMENT>(
     bulk_elem_pt,face_index);   
   
   // Add it to the mesh
   Lagrange_multiplier_mesh_pt->add_element_pt(el_pt);

Next we pass a pointer to the compound GeomObject that defines the desired shape of the FSI interface and specify which boundary in the "bulk" fluid mesh the element is attached to.

 
   // Set the GeomObject that defines the boundary shape and set
   // which bulk boundary we are attached to (needed to extract
   // the boundary coordinate from the bulk nodes)
   el_pt->set_boundary_shape_geom_object_pt(Solid_fsi_boundary_pt,b);

Finally, we apply boundary conditions for the Lagrange multipliers: we pin the Lagrange multipliers for nodes that are located on boundary 0 where the nodal displacements are pinned. (Recall that the Lagrange multipliers are additional degrees of freedom added to the "bulk" degrees of freedom originally created by the "bulk" element.)

   
   // Loop over the nodes to apply boundary conditions
   unsigned nnod=el_pt->nnode();
   for (unsigned j=0;j<nnod;j++)
    {
     Node* nod_pt = el_pt->node_pt(j);
     
     // Is the node also on boundary 0? 
     if (nod_pt->is_on_boundary(0))
      {
       // How many nodal values were used by the "bulk" element
       // that originally created this node?
       unsigned n_bulk_value=el_pt->nbulk_value(j);
       
        // The remaining ones are Lagrange multipliers and we pin them.
       unsigned nval=nod_pt->nvalue();
       for (unsigned j=n_bulk_value;j<nval;j++)
        {
         nod_pt->pin(j);
        }
      }
    }
  }
 
} // end of create_lagrange_multiplier_elements

Post-processing

The post-processing routine simply executes the output functions for the fluid and solid meshes and writes the results into separate files.

//==start_of_doc_solution=================================================
/// Doc the solution
//========================================================================
template<class FLUID_ELEMENT, class SOLID_ELEMENT>
void UnstructuredFSIProblem<FLUID_ELEMENT,SOLID_ELEMENT>::
doc_solution(DocInfo& doc_info)
{ 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned npts;
 npts=5; 
 
 // Output fluid solution 
 sprintf(filename,"%s/fluid_soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Fluid_mesh_pt->output(some_file,npts);
 some_file.close();
 
 
 // Output solid solution 
 sprintf(filename,"%s/solid_soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Solid_mesh_pt->output(some_file,npts);
 some_file.close();
 
 
} // end_of_doc_solution

Sanity check: Documenting the solid boundary coordinates

The function doc_solid_boundary_conditions() documents the parametrisation of the solid's FSI boundary in the file solid_boundary_test.dat. The file contains the solid's counterpart of the $[ x, y, \zeta ]$ data that we created for the fluid side of the FSI interface when setting up the fluid-structure interaction with FSI_functions::setup_fluid_load_info_for_solid_elements(...). The two parametrisations should be consistent; see What can go wrong? for more details.

The function also writes the file fsi_geom_object.dat, which may be used to check the integrity of the compound GeomObject
that represents the FSI interface of the solid: As $\zeta$ sweeps along the range used to parametrise the boundary, the position vector ${\bf R}(\zeta)$ , returned by GeomObject::position(...) should follow the FSI interface.

The implementation of the function is reasonably straightforward so we omit its listing here, see the source code for details.

Comments and Exercises

How the boundary coordinates are generated

The use of pseudo-elasticity for the node update in the fluid mesh makes the solution of FSI problems extremely straightforward. They key ingredient that allows the "automatic" coupling between the unstructured fluid and solid meshes
is the (consistent!) generation of the boundary coordinate $\zeta$ along the FSI interface. The function TriangleMesh::setup_boundary_coordinates(...) achieves this automatically and exploits the facts that

Meshes generated by Triangle are bounded by polygonal line segments.
Vertices in the polygonal domain boundary coincide with vertex nodes of the triangular finite elements.

The assignment of the boundary coordinate along mesh boundary b is performed as follows:

Attach FaceElements to the relevant faces of the "bulk" elements that are adjacent to mesh boundary b.
Establish the connectivity of the FaceElements using the fact that they share common Nodes and sort the elements into "connectivity" order around the boundary.
Locate the "lowest left" boundary node on the boundary and set its boundary coordinate to zero.
Step through the FaceElements (and their nodes) in order (taking into account that some FaceElements may be reversed relative to each other) and use the distance between adjacent nodes as the increment in the boundary coordinate.
Delete the FaceElements.

This procedure generates a consistent boundary parametrisation, irrespective of how many fluid and solid elements meet at the shared FSI boundary. This is because the nodes along all FaceElements are located along the same straight line segments. The method would not work if the boundary was curvilinear!

The method also fails, if the "lower left" boundary nodes identified in the two meshes are not located at the same position. This tends to happen if boundary nodes are assigned inconsistently, e.g. because the final node on the FSI interface was identified as being located on the appropriate mesh boundary in the fluid mesh but not in the solid mesh. In that case the boundary coordinates of the two meshes are offset relatively to each other by an amount equal to the distance between the respective "lower left" nodes.

Here is a plot of the boundary coordinate $\zeta$ generated from the fluid (blue) and solid (red) sides, with $\zeta$ being plotted "on top" of the unstructured solid mesh.

Plot of the boundary coordinates generated from the fluid and solid sides of the FSI interface.

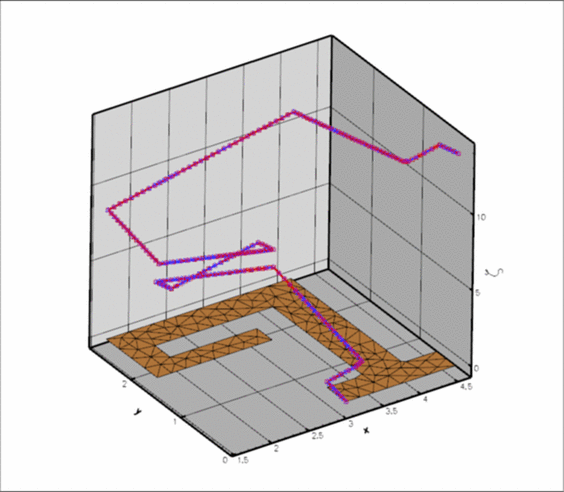
Fluid and solid meshes do not have to be matching

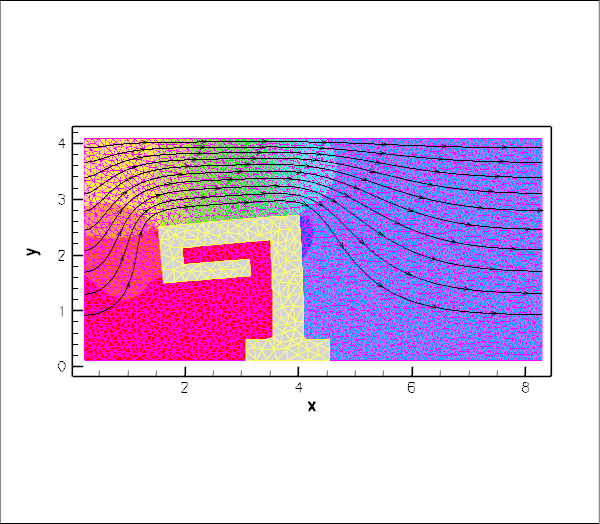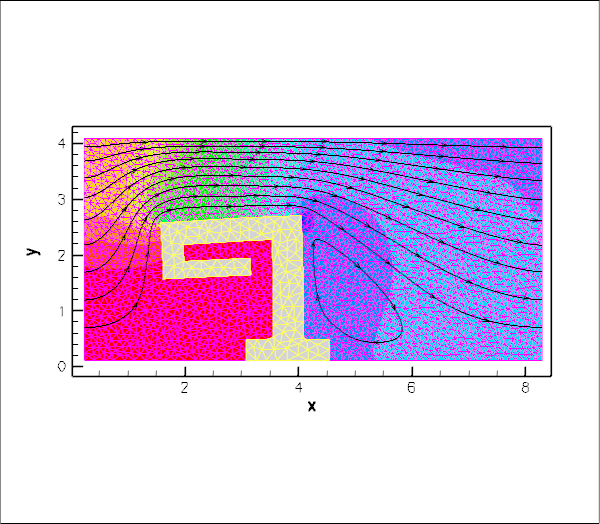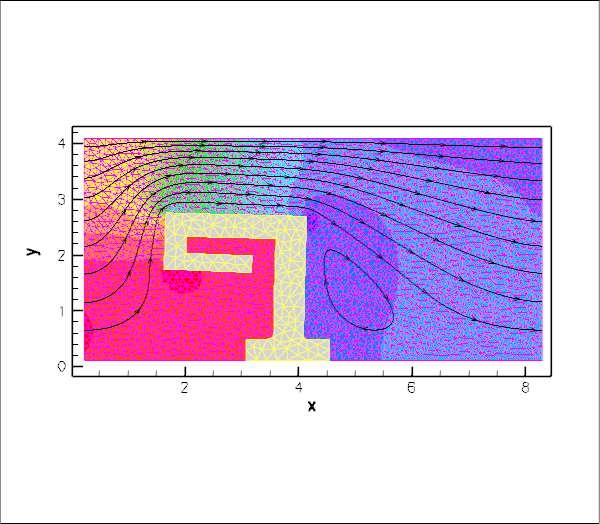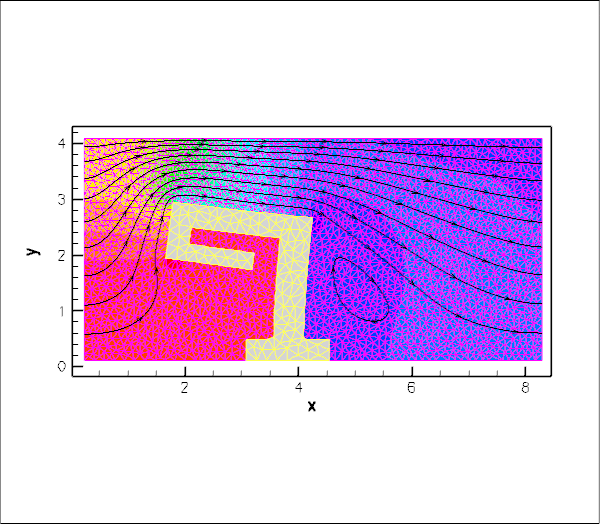
To demonstrate that the fluid and solid meshes to not have to be matching across the FSI interface, here are the results of another computation in which a much finer fluid mesh was used.

This computation was performed by re-generating the mesh, running triangle with a smaller maximum element size:

triangle -q -a0.01 fluid.fig.poly

The driver code remained completely unchanged.

Animation of the flow field (streamlines and pressure contours) and the deformation, computed on a refined fluid mesh.

Gravity only affects the solid – really?

The computations presented above suffer from a rather embarrassing modelling error. We have implicitly assumed that the solid is deformed significantly by gravity whereas no body force acts in the fluid. This is extremely unlikely to be right but makes for a useful exercise.

Formulate the problem properly, starting from the dimensional form of the governing equations, to determine the correct non-dimensional body forces for the fluid and the solid.
Use your analysis to explain under what circumstances our "error" could actually be a justifiable approximation to the real system.

What can go wrong?

As indicated above, the methodology employed in this tutorial makes the formulation of 2D FSI problems extremely straightforward. The most difficult part of the entire procedure is identifying the appropriate boundaries in the mesh generated by third-party software. Here are a few things that can (and often do) go wrong, which result in the code being unable to set up consistent boundary coordinates.

Boundaries don't match in xfig:

When drawing the boundaries of the fluid and solid domains in xfig, it is important to ensure that the FSI boundary is the same. A simple way to achieve this is to draw the fluid domain first and then make a copy of the resulting *.fig file. Once the file has been renamed it can be loaded into xfig and the polygonal vertices that are not part of the FSI interface can be deleted, while new vertices that are only part of the solid boundary can then be added. Just make sure that you don't move any of the vertices that define the FSI interface!

The mesh is too coarse for the automatic generation of boundary-lookup schemes:

Note: We believe that the problem described here has now been fixed. However, it is possible/likely that there are particularly pathological meshes in which the scheme fails. If you encounter any such problems, please let us know.

Another problem arises if the mesh generated by Triangle is too coarse for the automatic identification of mesh boundaries by TriangleMeshBase::setup_boundary_element_info(). This function gets (justifiably) confused when the mesh is so coarse that both vertex nodes on an element edge that crosses the interior of the domain are located on the same mesh boundary. We do not intend to fix this problem – if your mesh is that coarse, you should refine it! Anyway, if it happens, the problem may be diagnosed by plotting the output written to Multi_domain_functions::Doc_boundary_coordinate_file if this stream is open when FSI_functions::setup_fluid_load_info_for_solid_elements(...) is called. The file (fluid_boundary_test.dat in our driver code) contains the FaceElements that are attached to the (perceived) FSI boundary in the fluid mesh. (The file solid_boundary_test.dat, generated manually in our driver code, contains the same information for the solid mesh.)

Here is what the plot should look like if the fluid mesh is sufficiently fine (the FaceElements are shown as thick red lines on top of the "bulk" fluid mesh):

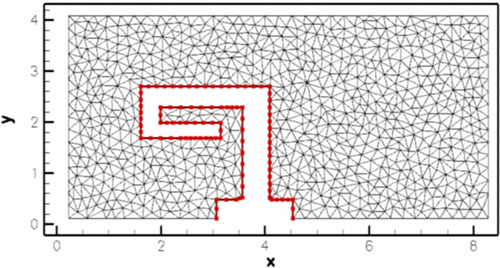Correct FSI boundary.

In the next figure, the fluid mesh is too coarse and the boundary detection has failed spectacularly:

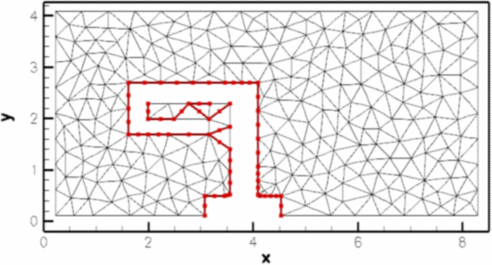Wrongly identified FSI boundary on a (too) coarse fluid mesh.

The boundary coordinates on the fluid and solid side of the FSI interface don't match:

We have already alluded to this problem when discussing How the boundary coordinates are generated. The problem arises mainly (only?) when nodes at the "end" of the FSI interface are only added to the FSI boundary in one of the meshes but not the other. For this reason, we strongly recommend printing out the mesh boundaries and checking them carefully before proceeding. Here is a plot of the mesh boundaries for the current problem:

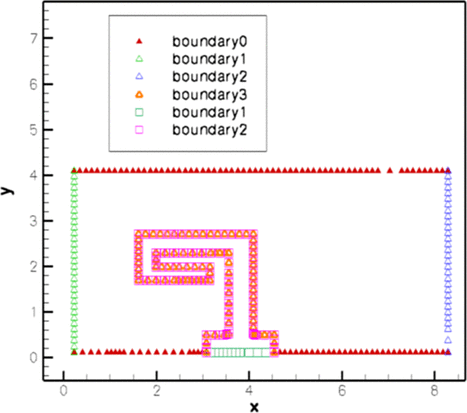Boundary nodes in the fluid (triangle) and solid (square) meshes.

Source files for this tutorial

The source files for this tutorial are located in the directory:

demo_drivers/interaction/unstructured_fsi
The driver code is:

demo_drivers/interaction/unstructured_fsi/unstructured_two_d_fsi.cc

PDF file

A pdf version of this document is available.