The purpose of this tutorial is to demonstrate how to impose the deformation of domain boundaries using Lagrange multipliers. This functionality is required, e.g. when using (pseudo-)solid mechanics to update the shape of the fluid mesh in fluid-structure interaction problems, say. (See Comments and Exercises for a discussion of an alternative, somewhat easier method for imposing boundary displacements in single-physics solid mechanics problems).

The model problem

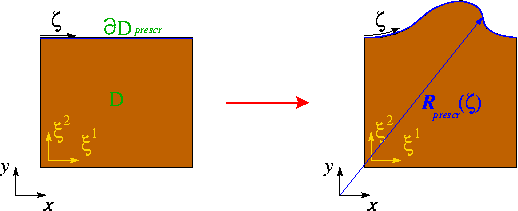
Here is a sketch of the model problem. A unit square is parametrised by two Lagrangian coordinates $(\xi^1,\xi^2)$ . Three of the four boundaries are held in a fixed position while the square's upper boundary $\partial D_{prescr}$ (which is parametrised by the boundary coordinate $\zeta$ ) is displaced to a new position given by ${\bf R}_{prescr}(\zeta)$ :

Sketch of the problem.

Theory and implementation

We identify the upper boundary by writing the Lagrangian coordinates of points on $\partial D_{prescr}$ as

$\left. \big( \xi^1, \xi^2\big)\right|_{\partial D_{prescr}} = \big( \xi^1_{\partial D_{prescr}}(\zeta), \xi^2_{\partial D_{prescr}}(\zeta) \big)$

which allows us to write the displacement constraint as

${\bf R}(\xi^1_{\partial D_{prescr}}(\zeta),\xi^2_{\partial D_{prescr}}(\zeta)) = {\bf R}_{prescr}(\zeta).$

We enforce this constraint by augmenting the principle of virtual displacements, discussed in the solid mechanics theory tutorial, by a Lagrange multiplier term so that it becomes

$\int \left\{ \sigma^{ij} \ \delta \gamma_{ij} - \left( {\bf f} - \Lambda^2 \frac{\partial^2 {\bf R}}{\partial t^2} \right) \cdot \delta {\bf R} \right\} \ dv - \oint_{A_{tract}} {\bf T} \cdot \delta {\bf R} \ dA \ + \ \delta \Pi_{constraint} = 0 \ \ \ \ \ \ \ \ (1)$

where

$\Pi_{constraint} = \int_{\partial D} \bigg( {\bf R}(\xi^1(\zeta),\xi^2(\zeta)) - {\bf R}_{prescr}(\zeta) \bigg) \cdot {\bf \Lambda} \ dS.$

Here

$dS = \left| \frac{d {\bf R}(\xi^1(\zeta),\xi^2(\zeta))}{d \zeta} \right| d\zeta$

is the differential of the arclength along the domain boundary and the vector ${\bf \Lambda}$ (not to be confused with the scalar $\Lambda^2$ which represents the non-dimensional density in (1)!) is the Lagrange multiplier – the surface traction to be applied to $\partial D_{prescr}$ to deform the boundary into the required shape.

We discretise this constraint by attaching FaceElements to the boundaries of the "bulk" solid elements that are adjacent to $\partial D_{prescr}$ . We denote the number of nodes in these FaceElements by and write the -th component of the discrete Lagrange multiplier stored at node as $L_{ij}$ . Thus the -th component of the Lagrange multiplier at local coordinate in the element is given by

$\Lambda_i = \sum_{j=1}^{N} L_{ij} \psi_j(s)$

where $\psi_j(s)$ is the shape function associated with node .

Upon taking the variations of the discretised constraint with respect to the unknown nodal positions and the discrete Lagrange multipliers we obtain (i) additional contributions to the residuals of the "bulk" solid mechanics equations (these may be interpreted as the virtual work done by the boundary tractions required to impose the prescribed boundary displacement) and (ii) the equations that impose the displacement constraints in weak form.

The actual implementation of this approach in oomph-lib is best thought of as a generalisation of the SolidTractionElements that are used to impose a prescribed traction to the boundary of a solid domain. The main difference is that in the ImposeDisplacementByLagrangeMultiplierElement, the imposed traction is one of the unknowns in the problem and must be determined via the displacement constraint, using the approach described above. The element introduces additional unknowns (the nodal values of the Lagrange multiplier) into the problem, therefore the ImposeDisplacementByLagrangeMultiplierElement resizes (increases) the number of values stored at the node from the value that was originally assigned by the "bulk" solid element it is attached to. (If the elements are used in a single-physics solid mechanics problem the discrete Lagrange multipliers are the only nodal values in the problem since the unknown nodal positions are stored in a separate Data item; cf. "Solid mechanics: Theory and implementation" for more details). The prescribed boundary shape ${\bf R}_{prescr}(\zeta)$ is provided by a GeomObject.

Results

The animation below shows the domain deformation in response to a prescribed boundary displacement given by

${\bf R}_{prescr}(\zeta)= \left( \begin{array}{c} \zeta \\ 1 \end{array} \right) + A \left( \begin{array}{c} 5 \zeta\ (\zeta-1) \ (\zeta-0.7) \\ \frac{1}{2}\left(1-\cos\left(2\pi\zeta\right)\right) \end{array} \right)$

With this choice the upper boundary remains flat (i.e. at ) when . As increases, the boundary is pulled upwards into a sinusoidal shape while simultaneously being pushed to the right. The vectors in the animation represent the Lagrange multipliers (i.e. the physical surface tractions) required to deform the domain into the required shape. Note how the automatic mesh adaptation refines the mesh in regions where the solid is strongly deformed.

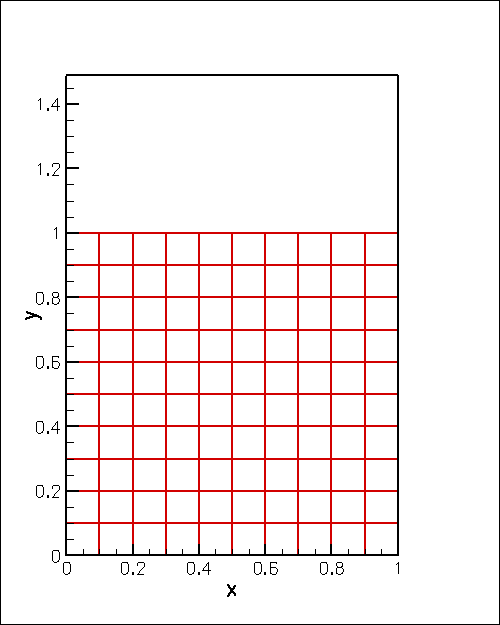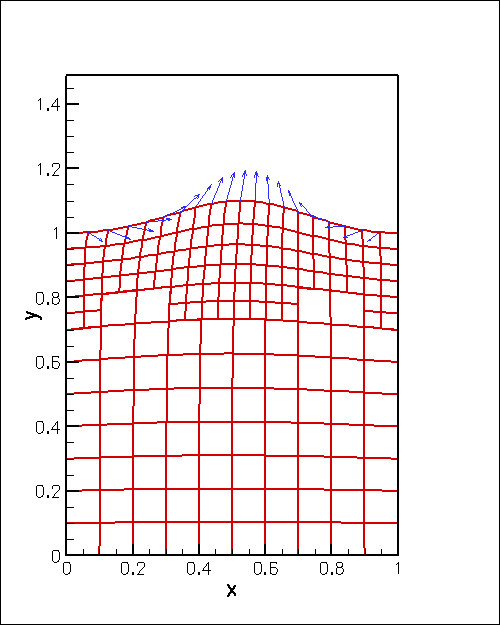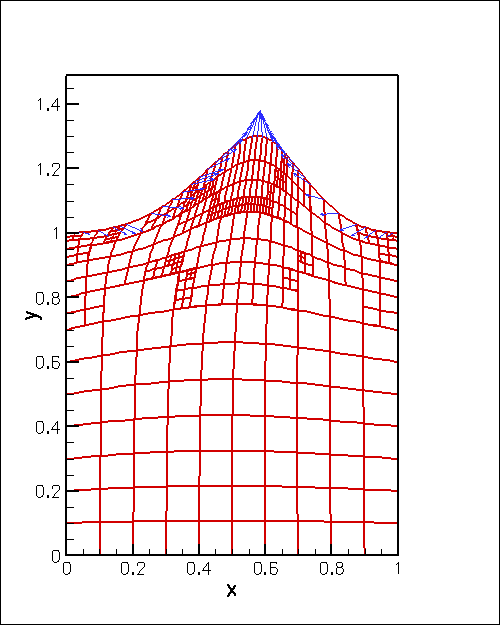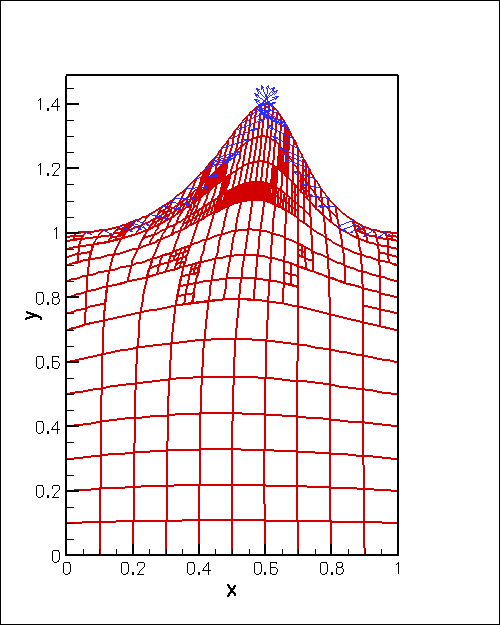
Domain deformation in response to the prescribed boundary displacement.

Describing the prescribed boundary motion with a GeomObject

Here is the implementation of the prescribed boundary shape as the WarpedLine, a two-dimensional GeomObject whose shape is parametrised by a single intrinsic coordinate.

//======Start_of_warped_line===============================================
/// Warped line in 2D space
//=========================================================================
class WarpedLine : public GeomObject
{
 
public:
 
 /// Constructor: Specify amplitude of deflection from straight horizontal line
 WarpedLine(const double& ampl) : GeomObject(1,2)
  {
   Ampl=ampl;
  }
 
 /// Broken copy constructor
 WarpedLine(const WarpedLine& dummy) 
  { 
   BrokenCopy::broken_copy("WarpedLine");
  } 
 
 /// Broken assignment operator
 void operator=(const WarpedLine&) 
  {
   BrokenCopy::broken_assign("WarpedLine");
  }
 
 
 /// Empty Destructor
 ~WarpedLine(){}
 
 /// Position vector at Lagrangian coordinate zeta 
 void position(const Vector<double>& zeta, Vector<double>& r) const
  {
   // Position vector
   r[0] = zeta[0]+5.0*Ampl*zeta[0]*(zeta[0]-1.0)*(zeta[0]-0.7);
   r[1] = 1.0+Ampl*0.5*(1.0-cos(2.0*MathematicalConstants::Pi*zeta[0]));
  }
 
 /// Parametrised position on object: r(zeta). Evaluated at
 /// previous timestep. t=0: current time; t>0: previous
 /// timestep. Forward to steady version
 void position(const unsigned& t, const Vector<double>& zeta,
                       Vector<double>& r) const
  {
   position(zeta,r);
  }
 
 /// Access to amplitude
 double& ampl() {return Ampl;}
 
 /// How many items of Data does the shape of the object depend on?
 /// None.
 unsigned ngeom_data() const
  {
   return 0;
  }
 
private:
 
 /// Amplitude of perturbation
 double Ampl;
 
};

Global parameters

As usual we define the problem parameters in a global namespace. We provide an instantiation of the GeomObject that defines the deformed boundary shape (setting its initial displacement amplitude to zero), and create an instance of oomph-lib's generalised Hookean constitutive equation with a Poisson ratio of 0.3 (recall that the use of the single-argument constructor for this constitutive equation implies that all stresses are non-dimensionalised on Young's modulus ; see the solid mechanics theory tutorial for details).

//=======start_namespace==========================================
/// Global parameters
//================================================================
namespace Global_Physical_Variables
{
 
 /// GeomObject specifying the shape of the boundary: Initially it's flat.
 WarpedLine Boundary_geom_object(0.0);
 
 /// Poisson's ratio
 double Nu=0.3;
 
 // Generalised Hookean constitutive equations
 GeneralisedHookean Constitutive_law(&Global_Physical_Variables::Nu);
 
} //end namespace

The driver code

We build an instantiation of the Problem class (described below), using nine-noded, two-dimensional RefineableQPVDElements to discretise the domain, and document the initial domain shape.

//=======start_of_main==================================================
/// Driver code
//======================================================================
int main()
{
 
 //Set up the problem
 PrescribedBoundaryDisplacementProblem<RefineableQPVDElement<2,3> > problem;
 
 // Doc initial domain shape
 problem.doc_solution();

We perform a parameter study, increasing the amplitude of the prescribed boundary deflection in small increments, while allowing one mesh adaptation per solution.

 
 // Max. number of adaptations per solve
 unsigned max_adapt=1;
 
 //Parameter incrementation
 unsigned nstep=2; 
 for(unsigned i=0;i<nstep;i++)
  {
   // Increment imposed boundary displacement
   Global_Physical_Variables::Boundary_geom_object.ampl()+=0.1;
 
   // Solve the problem with Newton's method, allowing
   // up to max_adapt mesh adaptations after every solve.
   problem.newton_solve(max_adapt);
   
   // Doc solution
   problem.doc_solution();

Since the main use of the methodology demonstrated here is in free-boundary problems where the solution of the solid problem merely serves to update the nodal positions in response to the prescribed boundary motion, we re-set the nodes' Lagrangian coordinates to their Eulerian positions after every solve. This makes the deformed configuration stress-free and tends to stabilise the computation, allowing larger domain deformations to be computed. We stress, however, that this renders the computed solutions physically meaningless in the sense that the domain shapes no longer represent the solution of the original elasticity problem for which the stress-free, undeformed configuration remains unchanged throughout the body's deformation.

 
   // For maximum stability: Reset the current nodal positions to be
   // the "stress-free" ones -- this assignment means that the
   // parameter study no longer corresponds to a physical experiment
   // but is what we'd do if we wanted to use the solid solve
   // to update a fluid mesh in an FSI problem, say.
   problem.solid_mesh_pt()->set_lagrangian_nodal_coordinates();
   
  }
 
} //end of main

The Problem class

The definition of the Problem class follows the usual pattern. We provide an access functions to the bulk mesh, as well as a few private helper functions that attach and detach the ImposeDisplacementByLagrangeMultiplierElements from the bulk mesh before and after the mesh adaptation.

//=============begin_problem============================================ 
/// Problem class for deformation of elastic block by prescribed
/// boundary motion.
//====================================================================== 
template<class ELEMENT>
class PrescribedBoundaryDisplacementProblem : public Problem
{
 
public:
 
 /// Constructor:
 PrescribedBoundaryDisplacementProblem();
 
 /// Update function (empty)
 void actions_after_newton_solve() {}
 
 /// Update function (empty)
 void actions_before_newton_solve() {}
 
 /// Access function for the solid mesh
 ElasticRefineableRectangularQuadMesh<ELEMENT>*& solid_mesh_pt() 
  {return Solid_mesh_pt;} 
 
 /// Actions before adapt: Wipe the mesh of Lagrange multiplier elements
 void actions_before_adapt();
 
 /// Actions after adapt: Rebuild the mesh of Lagrange multiplier elements
 void actions_after_adapt();
 
 /// Doc the solution
 void doc_solution();
 
private:
 
 /// Create elements that enforce prescribed boundary motion
 /// by Lagrange multiplilers
 void create_lagrange_multiplier_elements();
 
 /// Delete elements that enforce prescribed boundary motion
 /// by Lagrange multiplilers
 void delete_lagrange_multiplier_elements();
 
 /// Pointer to solid mesh
 ElasticRefineableRectangularQuadMesh<ELEMENT>* Solid_mesh_pt;
 
 /// Pointers to meshes of Lagrange multiplier elements
 SolidMesh* Lagrange_multiplier_mesh_pt;
 
 /// DocInfo object for output
 DocInfo Doc_info;
 
};

The Problem constructor

We start by creating the "bulk" mesh, discretising the domain with 5x5 elements of the type specified by the class's template argument.

//===========start_of_constructor======================================= 
/// Constructor: 
//====================================================================== 
template<class ELEMENT>
PrescribedBoundaryDisplacementProblem<ELEMENT>::PrescribedBoundaryDisplacementProblem() 
{
 
 // Create the mesh
 
 // # of elements in x-direction
 unsigned n_x=5;
 
 // # of elements in y-direction
 unsigned n_y=5;
 
 // Domain length in x-direction
 double l_x=1.0;
 
 // Domain length in y-direction
 double l_y=1.0;
 
 //Now create the mesh 
 solid_mesh_pt() = new ElasticRefineableRectangularQuadMesh<ELEMENT>(
  n_x,n_y,l_x,l_y);

Next we specify the error estimator, pass the pointer to the constitutive equation to the elements and perform one uniform mesh refinement:

 
 // Set error estimator
 solid_mesh_pt()->spatial_error_estimator_pt()=new Z2ErrorEstimator;
 
 //Assign the physical properties to the elements before any refinement
 //Loop over the elements in the main mesh
 unsigned n_element =solid_mesh_pt()->nelement();
 for(unsigned i=0;i<n_element;i++)
  {
   //Cast to a solid element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(solid_mesh_pt()->element_pt(i));
   
   // Set the constitutive law
   el_pt->constitutive_law_pt()=&Global_Physical_Variables::Constitutive_law;
  }
 
 // Refine the mesh uniformly
 solid_mesh_pt()->refine_uniformly();

We now create a new SolidMesh in which we store the elements that apply the displacement constraint. These elements are built (and added to the newly created SolidMesh) in the helper function create_lagrange_multiplier_elements(). Both meshes are then combined to the Problem's global mesh.

 
 // Construct the mesh of elements that enforce prescribed boundary motion
 // by Lagrange multipliers
 Lagrange_multiplier_mesh_pt=new SolidMesh;
 create_lagrange_multiplier_elements();
 
 // Solid mesh is first sub-mesh
 add_sub_mesh(solid_mesh_pt());
 
 // Add Lagrange multiplier sub-mesh
 add_sub_mesh(Lagrange_multiplier_mesh_pt);
 
 // Build combined "global" mesh
 build_global_mesh();

We pin the position of the nodes on all domain boundaries apart from the top boundary (boundary 2) and pin any redundant pressure degrees of freedom. (This is not strictly necessary in the present driver code since the displacement-based RefineableQPVDElements do not have any pressure degrees of freedom. However, it is good practice to do this anyway to guard against unpleasant surprises when the element type is changed at some point).

 
 // Pin nodal positions on all boundaries apart from the top one (2) 
 for (unsigned b=0;b<4;b++)
  {
   if (b!=2)
    {
     unsigned n_side = solid_mesh_pt()->nboundary_node(b);
     
     //Loop over the nodes
     for(unsigned i=0;i<n_side;i++)
      {
       solid_mesh_pt()->boundary_node_pt(b,i)->pin_position(0);
       solid_mesh_pt()->boundary_node_pt(b,i)->pin_position(1);
      }
    }
  }
 
 // Pin the redundant solid pressures (if any)
 PVDEquationsBase<2>::pin_redundant_nodal_solid_pressures(
  solid_mesh_pt()->element_pt());

Finally, we assign the equation numbers and specify the output directory.

 
 // Setup equation numbering scheme
 cout << "Number of dofs: " << assign_eqn_numbers() << std::endl; 
 
 // Set output directory
 Doc_info.set_directory("RESLT");
 
} //end of constructor

Actions before mesh adaptation

As usual, we remove the FaceElements that apply the displacement constraints before the bulk mesh is adapted.

//=====================start_of_actions_before_adapt======================
/// Actions before adapt: Wipe the mesh of elements that impose
/// the prescribed boundary displacements
//========================================================================
template<class ELEMENT>
void PrescribedBoundaryDisplacementProblem<ELEMENT>::actions_before_adapt()
{
 // Kill the  elements and wipe surface mesh
 delete_lagrange_multiplier_elements();
 
 // Rebuild the Problem's global mesh from its various sub-meshes
 rebuild_global_mesh();
 
}// end of actions_before_adapt

Actions after mesh adaptation

We re-attach the FaceElements that apply the displacement constraints once the bulk mesh has been adapted. Since the hanging status of nodes in the bulk mesh can change during the mesh adaptation it is again good practice to pin any nodal solid pressure values that may have become redundant.

//=====================start_of_actions_after_adapt=======================
///  Actions after adapt: Rebuild the mesh of elements that impose
/// the prescribed boundary displacements
//========================================================================
template<class ELEMENT>
void PrescribedBoundaryDisplacementProblem<ELEMENT>::actions_after_adapt()
{
 // Create the elements that impose the displacement constraint 
 // and attach them to the bulk elements that are
 // adjacent to boundary 2 
 create_lagrange_multiplier_elements();
 
 // Rebuild the Problem's global mesh from its various sub-meshes
 rebuild_global_mesh();
 
 // Pin the redundant solid pressures (if any)
 PVDEquationsBase<2>::pin_redundant_nodal_solid_pressures(
  solid_mesh_pt()->element_pt());
 
}// end of actions_after_adapt

Creating the Lagrange multiplier elements that impose the displacement constraint

The creation of the Lagrange multiplier elements that impose the displacement constraint follows the usual pattern. We loop over the "bulk" solid elements that are adjacent to mesh boundary 2 and attach ImposeDisplacementByLagrangeMultiplierElements to the appropriate faces.

//============start_of_create_lagrange_multiplier_elements===============
/// Create elements that impose the prescribed boundary displacement
//=======================================================================
template<class ELEMENT>
void PrescribedBoundaryDisplacementProblem<ELEMENT>::
create_lagrange_multiplier_elements()
{
 // Lagrange multiplier elements are located on boundary 2:
 unsigned b=2;
 
 // How many bulk elements are adjacent to boundary b?
 unsigned n_element = solid_mesh_pt()->nboundary_element(b);
 
 // Loop over the bulk elements adjacent to boundary b?
 for(unsigned e=0;e<n_element;e++)
  {
   // Get pointer to the bulk element that is adjacent to boundary b
   ELEMENT* bulk_elem_pt = dynamic_cast<ELEMENT*>(
    solid_mesh_pt()->boundary_element_pt(b,e));
   
   //Find the index of the face of element e along boundary b
   int face_index = solid_mesh_pt()->face_index_at_boundary(b,e);
      
   // Create new element and add to mesh
   Lagrange_multiplier_mesh_pt->add_element_pt(
    new ImposeDisplacementByLagrangeMultiplierElement<ELEMENT>(
     bulk_elem_pt,face_index));   
  }  

Next we loop over the newly-created
ImposeDisplacementByLagrangeMultiplierElements and specify the GeomObject that defines the imposed boundary displacements. We also specify which boundary of the bulk mesh the ImposeDisplacementByLagrangeMultiplierElements are located on. This is required to enable the ImposeDisplacementByLagrangeMultiplierElements to extract the appropriate boundary coordinate from its constituent nodes. (We discussed elsewhere that boundary coordinates are usually defined (and passed to the nodes) when the nodes are first created, typically during the construction of the bulk mesh. Since nodes can be located on multiple domain boundaries, each boundary coordinate is associated with a particular boundary number. Passing this number to the ImposeDisplacementByLagrangeMultiplierElements allows them to obtain the correct boundary coordinate from the node.)

 
 
 // Loop over the elements in the Lagrange multiplier element mesh
 // for elements on the top boundary (boundary 2)
 n_element=Lagrange_multiplier_mesh_pt->nelement();
 for(unsigned i=0;i<n_element;i++)
  {
   //Cast to a Lagrange multiplier element
   ImposeDisplacementByLagrangeMultiplierElement<ELEMENT> *el_pt = 
    dynamic_cast<ImposeDisplacementByLagrangeMultiplierElement<ELEMENT>*>
    (Lagrange_multiplier_mesh_pt->element_pt(i));
 
   // Set the GeomObject that defines the boundary shape and
   // specify which bulk boundary we are attached to (needed to extract
   // the boundary coordinate from the bulk nodes)
   el_pt->set_boundary_shape_geom_object_pt( 
    &Global_Physical_Variables::Boundary_geom_object,b);

Finally, we impose boundary conditions for the Lagrange multipliers. Their values must be pinned (and set to zero) at the left and right ends of the upper mesh boundary (boundary 2), since the displacement of the nodes at these points is already enforced by the boundary conditions imposed at the left and right vertical boundaries (boundaries 1 and 3).

We discussed above that the discrete Lagrange multipliers are added to any already existing nodal degrees of freedom when the ImposeDisplacementByLagrangeMultiplierElements are attached to the faces of the "bulk" solid elements. The number of nodal values that were stored at an element's j -th node before the additional nodal values were added, can be obtained from the function nbulk_value(j), defined in the FaceElement base class. We pin the Lagrange multipliers at the "corner nodes" by looping over all nodes in the ImposeDisplacementByLagrangeMultiplierElements and pinning the additional nodal values of any nodes that are located on mesh boundaries 1 or 3.

   
   // Loop over the nodes 
   unsigned nnod=el_pt->nnode();
   for (unsigned j=0;j<nnod;j++)
    {
     Node* nod_pt = el_pt->node_pt(j);
     
     // Is the node also on boundary 1 or 3?
     if ((nod_pt->is_on_boundary(1))||(nod_pt->is_on_boundary(3)))
      {
       // How many nodal values were used by the "bulk" element
       // that originally created this node?
       unsigned n_bulk_value=el_pt->nbulk_value(j);
       
       // The remaining ones are Lagrange multipliers and we pin them.
       unsigned nval=nod_pt->nvalue();
       for (unsigned j=n_bulk_value;j<nval;j++)
        {
         nod_pt->pin(j);
        }
      }
    }
  }
  
} // end of create_lagrange_multiplier_elements

Deleting the Lagrange multiplier elements that impose the displacement constraint

The function delete_lagrange_multiplier_elements() deletes the Lagrange multiplier elements that impose the displacement constraint and flushes the associated mesh.

//====start_of_delete_lagrange_multiplier_elements=======================
/// Delete elements that impose the prescribed boundary displacement
/// and wipe the associated mesh
//=======================================================================
template<class ELEMENT>
void PrescribedBoundaryDisplacementProblem<ELEMENT>::delete_lagrange_multiplier_elements()
{
 // How many surface elements are in the surface mesh
 unsigned n_element = Lagrange_multiplier_mesh_pt->nelement();
 
 // Loop over the surface elements
 for(unsigned e=0;e<n_element;e++)
  {
   // Kill surface element
   delete Lagrange_multiplier_mesh_pt->element_pt(e);
  }
 
 // Wipe the mesh
 Lagrange_multiplier_mesh_pt->flush_element_and_node_storage();
 
} // end of delete_lagrange_multiplier_elements

Post-processing

The function doc_solution() outputs the shape of the deformed body and the Lagrange multiplier along the upper boundary.

//==============start_doc===========================================
/// Doc the solution
//==================================================================
template<class ELEMENT>
void PrescribedBoundaryDisplacementProblem<ELEMENT>::doc_solution()
{
 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned n_plot = 5; 
 
 
 // Output shape of deformed body
 //------------------------------
 sprintf(filename,"%s/soln%i.dat",Doc_info.directory().c_str(),
         Doc_info.number());
 some_file.open(filename);
 solid_mesh_pt()->output(some_file,n_plot);
 some_file.close();
 
 // Output Lagrange multipliers
 //----------------------------
 sprintf(filename,"%s/lagr%i.dat",Doc_info.directory().c_str(),
         Doc_info.number());
 some_file.open(filename);
 
 // This makes sure the elements are ordered in same way every time
 // the code is run -- necessary for validation tests.
 std::vector<FiniteElement*> el_pt;
 unsigned nelem=Lagrange_multiplier_mesh_pt->nelement();
 for (unsigned e=0;e<nelem;e++)
  {
   el_pt.push_back(Lagrange_multiplier_mesh_pt->finite_element_pt(e));
  }
 std::sort(el_pt.begin(),el_pt.end(),FiniteElementComp());
 for (unsigned e=0;e<nelem;e++)
  {
   el_pt[e]->output(some_file);
  }
 some_file.close();
 
 // Increment label for output files
 Doc_info.number()++;
 
} //end doc

Comments and Exercises

Comments

As mentioned in the introduction, there is an alternative, much simpler way of imposing prescribed boundary motions which does not require Lagrange multipliers: Pin the nodal positions of all nodes on $\partial D_{prescr}$ and update their positions manually before calling the Newton solver, e.g. by changing the actions_before_newton_solve() function to

 /// Update boundary position directly
 void actions_before_newton_solve()
  {
 
   // Loop over all nodes on top boundary (boundary 2)
   unsigned b=2;
   unsigned n_nod = solid_mesh_pt()->nboundary_node(b);
   for(unsigned i=0;i<n_nod;i++)
    {
     Node* nod_pt= solid_mesh_pt()->boundary_node_pt(b,i);
 
     // Get boundary coordinate associated with boundary 2
     Vector<double> zeta(1);
     nod_pt->get_coordinates_on_boundary(b,zeta);
 
     // Get prescribed position from GeomObject
     Vector<double> r(2);
     Global_Physical_Variables::Boundary_geom_object.position(zeta,r);
 
     // Update position
     nod_pt->x(0)=r[0];
     nod_pt->x(1)=r[1];
    }
 
  } // end actions_before_newton_solve

This approach is implemented in the alternative driver code prescribed_displ_lagr_mult2.cc.

Exercises

In order to familiarise yourself with the details of how FaceElements add additional nodal values to the nodes they are attached to, output the values of n_bulk_value and nval in the loop that pins the Lagrange multipliers in create_lagrange_multiplier_elements(). Explain why, for the RefineableQPVDElement<2,3> used here, we have n_bulk_value = 0. What happens if you use elements of type RefineableQPVDElementWithContinousPressure<2> instead?
Comment out the call to set_lagrangian_nodal_coordinates() after the solve and compare the robustness of the computation and the resulting domain shapes. [Hint: You will have to reduce the increment for the amplitude of the prescribed boundary deflection to 0.025 or less, otherwise the Newton iteration will diverge very rapidly.]
Explore the performance of the alternative driver code (without the use of Lagrange multipliers) prescribed_displ_lagr_mult2.cc and explain why it is less robust than the version with Lagrange multipliers (in the sense that the increment in the amplitude of the prescribed boundary displacement has to be reduced significantly to keep the Newton method from diverging). Hint: Compare the domain shapes before the call to the Newton solver.
Omit the specification of the boundary number in the bulk mesh by commenting out the call to set_boundary_number_in_bulk_mesh(...) in the function create_lagrange_multiplier_elements(). Check what happens when the code is compiled with and without the PARANOID flag.

PDF file

A pdf version of this document is available.