Demo problem: How to create refineable meshes in domains with curvilinear and/or moving boundaries

In an earlier example we demonstrated how easy it is to "upgrade" an existing quad mesh to a RefineableMesh that can be used with oomph-lib's mesh adaptation routines. The "upgrade" was achieved by multiple inheritance: We combined the basic (non-refineable) mesh object with oomph-lib's RefineableQuadMesh – a class that implements the required mesh adaptation procedures, using QuadTree - based refinement techniques for meshes that contain quadrilateral elements. During the refinement process, selected elements are split into four "son" elements and the nodal values and coordinates of any newly created nodes are determined by interpolation from the "father" element. This procedure is perfectly adequate for problems with polygonal domain boundaries in which the initial coarse mesh provides a perfect representation of the domain. The situation is more complicated in problems with curvilinear domain boundaries since we must ensure that successive mesh refinements lead to an increasingly accurate representation of the domain boundary.

To illustrate these issues we (re-)consider the 2D Poisson problem

Two-dimensional model Poisson problem in a non-trivial domain
Solve

\[ \sum_{i=1}^2 \frac{\partial^2u}{\partial x_i^2} = -1, \ \ \ \ \ \ \ \ \ \ (1) \]

in the fish-shaped domain $D_{fish} $ with homogeneous Dirichlet boundary conditions

\[ \left. u\right|_{\partial D_{fish}}=0. \ \ \ \ \ \ \ \ \ \ (2) \]



In Part 1 of this document we shall explain how oomph-lib's mesh adaptation procedures employ the Domain and MacroElement objects to adapt meshes in domains with curvilinear boundaries. In Part 2, we demonstrate how to create new Domain objects.

Part 1: Mesh adaptation in domains with curvilinear boundaries, using Domain and MacroElement objects

The plot below shows the domain $D_{fish} $, represented by the multi-coloured, shaded region and its (extremely coarse) discretisation with four four-node quad elements. The elements' edges and nodes are shown in black.

The fish-shaped domain and its discretisation with four four-node quad elements

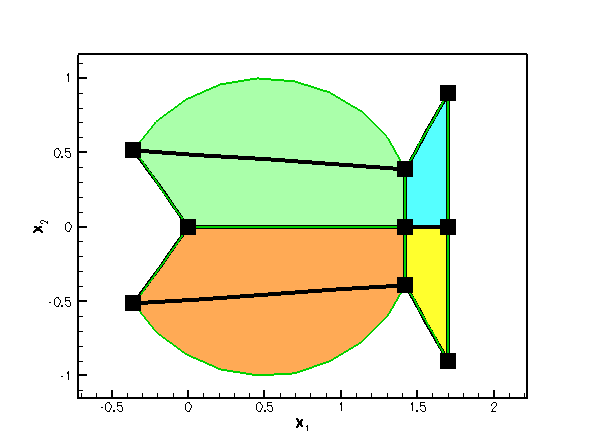
Obviously, the curvilinear boundaries of the fish-shaped domain (arcs of circles) are very poorly resolved by the elements' straight edges. Simple mesh adaptation, based on the techniques described in the earlier example will not result in convergence to the exact solution since the refined mesh never approaches the exact domain geometry:

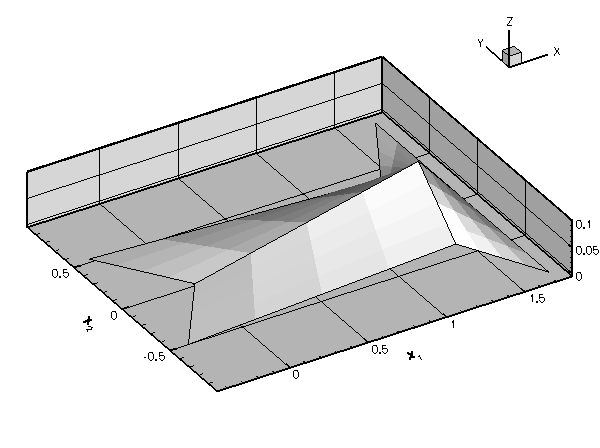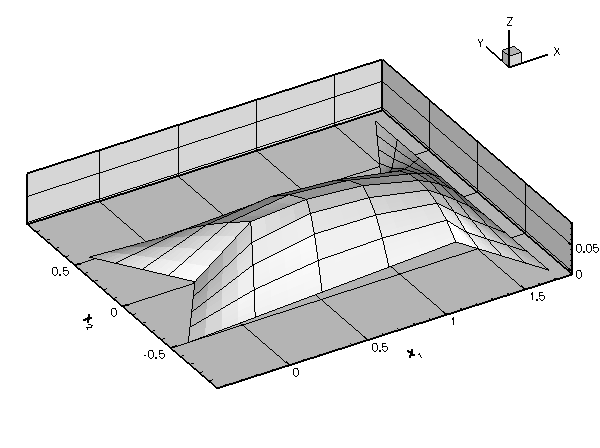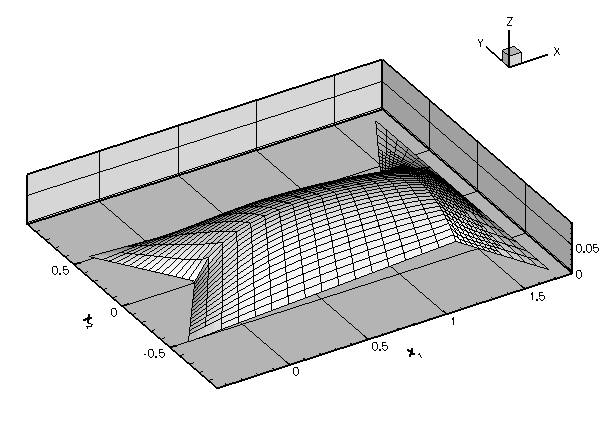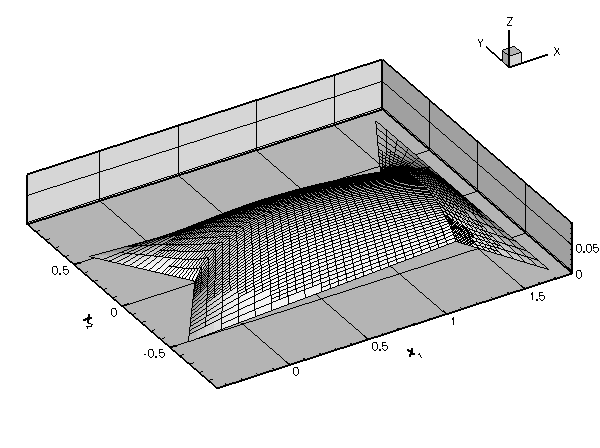
Plot of the mesh adaptation without MacroElements

To overcome this problem, the mesh adaptation routines must be given access to an exact, analytical representation of the actual domain. This is the purpose of oomph-lib's Domain object. A Domain provides an analytical description of a mathematical domain, by decomposing it into a number of so-called MacroElements. Each MacroElement provides a mapping between a set of local and global coordinates $ {\bf r}_{macro}({\bf s})$ – similar to the mapping between the local and global coordinates in a finite element. The key difference between the two types of element is that the MacroElement mapping resolves curvilinear domain boundaries exactly, whereas the finite element mapping interpolates the global coordinates between the coordinates of its nodes. The topology of MacroElements mirrors that of the associated (geometric) finite elements: For instance, the QMacroElement family is the counterpart of the QElement family of geometric finite elements. Both are templated by the spatial dimension, and the local coordinates (in their right-handed local coordinate systems) are in the range between -1 and +1.

The different-coloured, shaded regions in the above sketch represent the four two-dimensional QMacroElements by which the FishDomain represents the fish-shaped domain $ D_{fish} $. For instance, MacroElement 0 (shown in orange) represents the lower half of the fish's body; within this MacroElement, the curved "belly" is represented by the line $ {\bf r}_{macro}(s_0,s_1=-1)$ for $s_0\in[-1,1]$; the lower "jaw" is represented by $ {\bf r}_{macro}(s_0=-1,s_1)$ for $s_1\in[-1,1]$; etc.

To illustrate the use of MacroElements / Domains, the following code fragment (from
fish_mesh.template.cc ) demonstrates how the constructor of the original, non-refineable FishMesh assigns the nodal positions. Each of the FishDomain's four QMacroElements is associated with one of the four finite elements in the mesh. Since both types of elements are parametrised by the same local coordinate systems, we determine the position of the node that is located at $(s_0, s_1)$ (in the finite element's local coordinate system) from the corresponding MacroElement mapping, ${\bf r}_{macro}(s_0, s_1)$:

// Create elements and all nodes in element
//-----------------------------------------
// (ignore repetitions for now -- we'll clean them up later)
//----------------------------------------------------------
for (unsigned e = 0; e < nelem; e++)
{
// Create element
Element_pt[e] = new ELEMENT;
// Loop over rows in y/s_1-direction
for (unsigned i1 = 0; i1 < n_node_1d; i1++)
{
// Loop over rows in x/s_0-direction
for (unsigned i0 = 0; i0 < n_node_1d; i0++)
{
// Local node number
unsigned j_local = i0 + i1 * n_node_1d;
// Create the node and store pointer to it
Node* node_pt =
finite_element_pt(e)->construct_node(j_local, time_stepper_pt);
// Work out the node's coordinates in the finite element's local
// coordinate system:
finite_element_pt(e)->local_fraction_of_node(j_local, s_fraction);
s[0] = -1.0 + 2.0 * s_fraction[0];
s[1] = -1.0 + 2.0 * s_fraction[1];
// Get the global position of the node from macro element mapping
Domain_pt->macro_element_pt(e)->macro_map(s, r);
// Set the nodal position
node_pt->x(0) = r[0];
node_pt->x(1) = r[1];
}
}
} // end of loop over elements

This technique ensures that the mesh's boundary nodes are placed on the exact domain boundary when the mesh is created.

To retain this functionality during the mesh adaptation, each FiniteElement provides storage for a pointer to an associated MacroElement. By default, the MacroElement pointer is set to NULL, indicating that the element is not associated with a MacroElement. In that case, the coordinates of newly created nodes are determined by interpolation from the father element, as discussed above. If the MacroElement pointer is non-NULL, the refinement process refers to the element's MacroElement representation to determine the new nodal positions.

To enable the mesh adaptation process to respect the domain's curvilinear boundaries, each element in the coarse base mesh must therefore be given a pointer to its associated MacroElement, e.g. by using the following loop:

// Loop over all elements and set macro element pointer
unsigned n_element = this->nelement();
for (unsigned e = 0; e < n_element; e++)
{
// Get pointer to element
FiniteElement* el_pt = this->finite_element_pt(e);
// Set pointer to macro element to enable MacroElement-based
// remesh. Also enables the curvlinear boundaries
// of the mesh/domain get picked up during adaptive
// mesh refinement in derived classes.
el_pt->set_macro_elem_pt(this->Domain_pt->macro_element_pt(e));
}

Once the mesh is aware of the curvilinear boundaries, each level of mesh refinement produces a better representation of the curvilinear domain, ensuring the convergence to the exact solution:

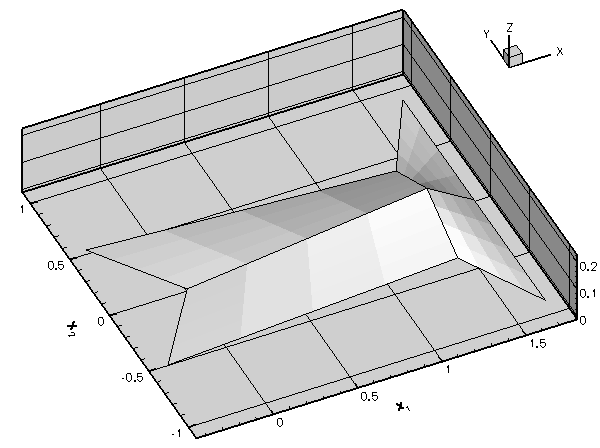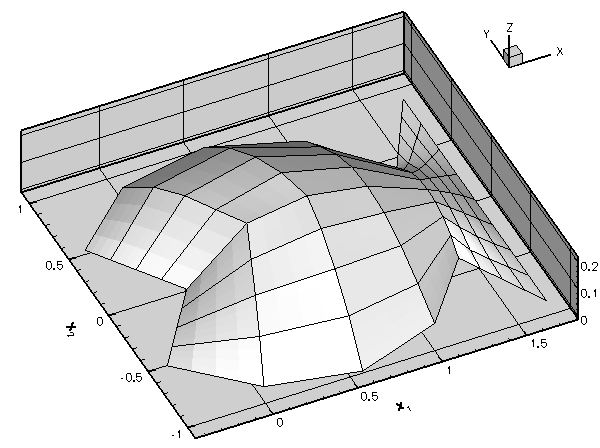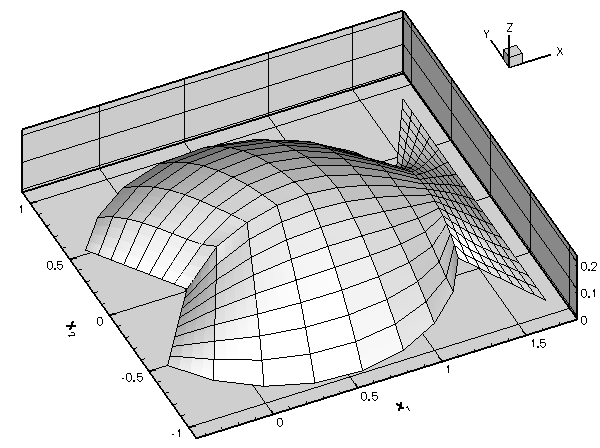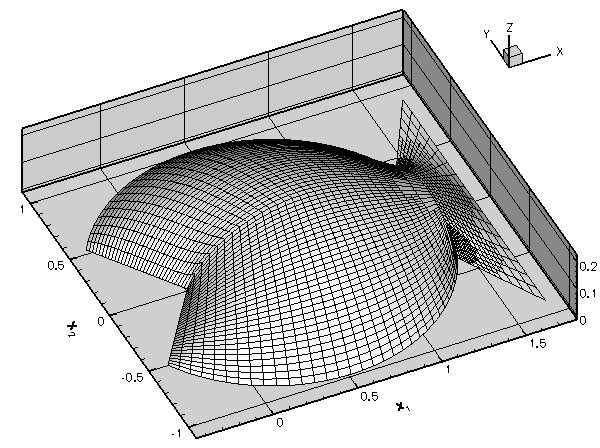
Plot of the mesh adaptation with MacroElements

The results shown in this animation were computed with the demo code fish_poisson_adapt.cc – a simple modification of the code
fish_poisson.cc that we used in the earlier example. The only difference between the two codes is that in the present example, the FishDomain is discretised with four-node rather than nine-node RefineableQPoissonElements to highlight the inadequacy of the basic mesh refinement process. Note that, as a result of lower accuracy of the four-node elements, we require a much finer discretisation in the interior of the domain.

Part 2: How to represent domains with curvilinear boundaries by Domain and MacroElement objects

The above example demonstrated that "upgrading" existing meshes to RefineableMeshes that can be used with oomph-lib's mesh adaptation procedures, can be achieved in two trivial steps:

  1. Associate each RefineableQElement with a QuadTree – this can done completely automatically by calling the function RefineableQuadMesh::setup_quadtree_forest().
  2. If the problem's domain has curvilinear boundaries, associate each RefineableQElement with a MacroElement – defined in the Domain object that provides an
    analytical representation of the domain.

While this looks (and indeed is) impressively simple, we still have to explain how to create Domain objects. We start by introducing yet another useful oomph-lib class, the GeomObject.

The geometric object, GeomObject

As the name suggests, GeomObjects are oomph-lib objects that provide an analytical description/parametrisation of geometric objects. Mathematically, GeomObjects define a mapping from a set of "Lagrangian" (intrinsic) coordinates to the global "Eulerian" coordinates of the object. The number of Lagrangian and Eulerian coordinates can differ. For instance, the unit circle, centred at the origin may be parametrised by a single coordinate, $ \xi $ (representing the polar angle), as

\[ {\bf r}_{circle} = \left( \begin{array}{c} \cos \xi \\ \sin \xi \end{array} \right), \]

while a 2D disk may be parametrised by two coordinates $ \xi_1 $ and $ \xi_2 $ (representing the radius and the polar angle, respectively) as

\[ {\bf r}_{disk} = \xi_1 \left( \begin{array}{c} \cos \xi_2 \\ \sin \xi_2 \end{array} \right). \]

All specific GeomObjects must implement the pure virtual function GeomObject::position(...) which computes the Eulerian position vector $ {\bf r}$ as a function of the (vector of) Lagrangian coordinates $ {\bf \xi}$. (The GeomObject base class also provides interfaces for a multitude of other functions, such as functions that compute the spatial and temporal derivatives of the position vector. These functions are implemented as "broken" virtual functions and their implementation is optional; see the earlier example for a discussion of "broken" virtual functions.)

Here is a complete example of a specific GeomObject:

//=======================start_of_unit_circle==============================
/// Unit circle in 2D, centred at the origin, parametrised by a single
/// Lagrangian coordinate, the polar angle.
//=========================================================================
class UnitCircle : public GeomObject
{
public:
/// Constructor: Pass the number of Lagrangian
/// and Eulerian coordinates to the constructor of the
/// GeomObject base class.
UnitCircle() : GeomObject(1,2) {}
/// Destructor -- emtpy
virtual ~UnitCircle(){}
/// Position vector, r, to the point on the circle identified by
/// its 1D Lagrangian coordinate, xi (passed as a 1D Vector):
void position(const Vector<double>& xi, Vector<double>& r) const
{
// Eulerian position vector
r[0] = cos(xi[0]);
r[1] = sin(xi[0]);
}
/// Position vector, r, to the point on the circle identified by
/// its 1D Lagrangian coordinate, xi (passed as a 1D Vector) at discrete time
/// level t (t=0: present; t>0: previous). The shape of the object
/// is not time-dependent, therefore we forward this call to the
/// steady version.
void position(const unsigned& t, const Vector<double>& xi,
Vector<double>& r) const
{
position(xi,r);
}
}; // end of unit circle class
UnitCircle
Unit circle in 2D, centred at the origin, parametrised by a single Lagrangian coordinate,...
Definition: fish_domain.cc:44
UnitCircle::UnitCircle
UnitCircle()
Constructor: Pass the number of Lagrangian and Eulerian coordinates to the constructor of the GeomObj...
Definition: fish_domain.cc:51
UnitCircle::~UnitCircle
virtual ~UnitCircle()
Destructor – emtpy.
Definition: fish_domain.cc:54
UnitCircle::position
void position(const Vector< double > &xi, Vector< double > &r) const
Position vector, r, to the point on the circle identified by its 1D Lagrangian coordinate,...
Definition: fish_domain.cc:58

[The dummy time-dependent version of the position(...) function is required to stop the compiler from complaining about "only partially overridden" virtual functions].

Domains

GeomObjects provide a natural way of representing a Domain's curvilinear boundaries. For instance, the fish's body in $ D_{fish}$ is bounded by two circular arcs. These may be represented by GeomObjects of type Circle – a slight generalisation of the UnitCircle class shown above. The FishDomain constructor therefore takes a pointer to a 2D GeomObject and the "start" and "end" values of the Lagrangian coordinate along this object. The GeomObject represents the curvilinear boundary of the fish's (upper) body and the two coordinates represent the Lagrangian coordinates of the "nose" and the "tail" on this GeomObject, as shown in this sketch:

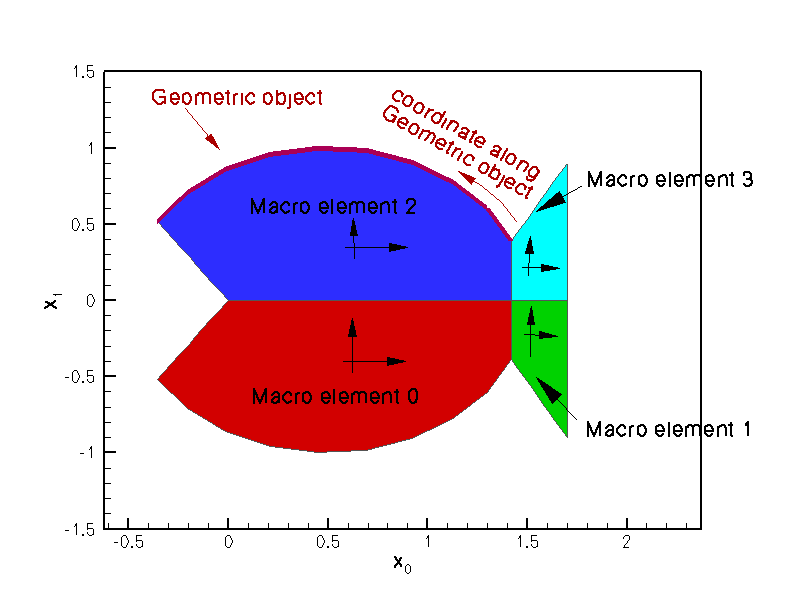
The fish-shaped domain and its MacroElement-based representation by the FishDomain object. The arrows show the orientation of the MacroElements' local coordinate systems.

To construct a FishDomain whose curvilinear boundaries are arcs of unit circles, centred at $ (x_0,x_1) = (1/2 , 0) $ we create a GeomObject of type Circle, passing the appropriate parameters to its constructor:

// Fish back is a circle of radius 1, centred at (0.5,0.0)
double x_c=0.5;
double y_c=0.0;
double r_back=1.0;
GeomObject* back_pt=new Circle(x_c,y_c,r_back);

Next, we pass the (pointer to the) Circle object to the constructor of the FishDomain, locating the "nose end" of the fish's back at $\xi=2.4$ and its "tail end" at $\xi=0.4$:

double xi_nose=2.6;
double xi_tail=0.4;
Domain* domain_pt=new FishDomain(back_pt,xi_nose,xi_tail);

To see how this works internally, let us have a look at the FishDomain constructor. The constructor stores the pointer to the fish's "back", and the start and end values of the Lagrangian coordinates in the private data members Back_pt, Xi_nose and Xi_tail. Next we set some additional parameters, that define the geometry (the mouth is located at the origin; the fin is a vertical line at $ x=1.7$, ranging from $ y=-0.9$ to $ y=+0.9$). Finally, we allocate storage for the four MacroElements and build them. Note that the constructor of the MacroElement takes a pointer to the Domain, and the MacroElement's number within that Domain:

/// Constructor: Pass pointer to GeomObject that represents the
/// (upper) curved boundary of the fish's body, and the start and end values
/// of the Lagrangian coordinates along the GeomObject.
FishDomain(GeomObject* back_pt,
const double& xi_nose,
const double& xi_tail)
: Xi_nose(xi_nose), Xi_tail(xi_tail), Back_pt(back_pt)
{
// Set values for private data members that are describe
// geometric features of the fish: x-coordinate of the fin,
// (half-)height of the fin, and x-position of the mouth.
X_fin = 1.7;
Y_fin = 0.9;
X_mouth = 0.0;
// There are four macro elements
unsigned nmacro = 4;
Macro_element_pt.resize(nmacro);
// Build them
for (unsigned i = 0; i < nmacro; i++)
{
Macro_element_pt[i] = new QMacroElement<2>(this, i);
}
} // end of constructor

Most of the remaining public member functions are equally straightforward. We provide various access functions to the geometric parameters such as X_mouth, etc – we will not list these explicitly. All the "real work" is done in the implementation of the pure virtual function Domain::macro_element_boundary(...). Given

  • the number of the MacroElement in its Domain
  • the direction of its boundary (N[orth], S[outh], E[ast], W[est], enumerated in the namespace QuadTreeNames)

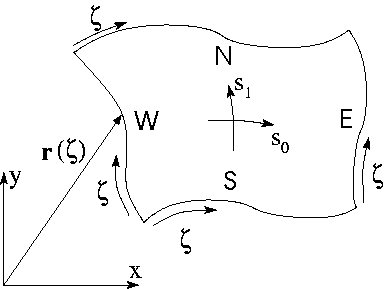
this function must compute the vector $ {\bf r}(\zeta)$ to the MacroElement's boundary. Here $ \zeta \in [-1,1]$ is the 1D coordinate along the element boundary, aligned with the direction of the MacroElement's 2D coordinates $(s_0,s_1) $ as indicated in this sketch:

Sketch illustrating the parametrisation of the MacroElement's four boundaries.

Since the shape of the domain can evolve in time, the full interface for the function includes an additional parameter, t, which indicates the (discrete) time level at which the domain shape is to be evaluated. If t=0 the function computes the domain shape at the current time; if t>0 it computes the shape at the t -th previous timestep. (Another example in which we solve the unsteady heat equation in a moving domain, provides a a more detailed discussion of this aspect.) Here is the full interface for the FishDomain::macro_element_boundary(...) function:

/// Vector representation of the i_macro-th macro element
/// boundary i_direct (N/S/W/E) at the discrete time level t
/// (t=0: present; t>0: previous): \f$ {\bf r}({\bf zeta}) \f$
/// Note that the local coordinate \b zeta is a 1D
/// Vector rather than a scalar -- this is unavoidable because
/// this function implements the pure virtual function in the
/// Domain base class.
void macro_element_boundary(const unsigned& t,
const unsigned& i_macro,
const unsigned& i_direct,
const Vector<double>& zeta,
Vector<double>& r);

The implementation of this function is the only tedious task that needs to be performed by the "mesh writer". Once Domain::macro_element_boundary(...) is implemented, the Domain's constituent MacroElements can refer to this function to establish the positions of their boundaries (recall that we passed the pointer to the Domain and the MacroElement's number in the Domain to the MacroElement constructor). The MacroElement::macro_map(...) functions interpolate the position of the MacroElement's boundaries into their interior.

To illustrate the general procedure, here is the complete listing of the FishDomain::macro_element_boundary(...) function. The function employs switch statements to identify the private member functions that provide the parametrisation of individual MacroElement boundaries. Some of these functions are listed below.

//==========start_of_macro_element_boundary========================
/// Vector representation of the imacro-th macro element
/// boundary idirect (N/S/W/E) at time level t
/// (t=0: present; t>0: previous): \f$ {\bf r}({\bf zeta}) \f$
/// Note that the local coordinate \b zeta is a 1D
/// Vector rather than a scalar -- this is unavoidable because
/// this function implements the pure virtual function in the
/// Domain base class.
//=================================================================
void FishDomain::macro_element_boundary(const unsigned& t,
const unsigned& imacro,
const unsigned& idirect,
const Vector<double>& zeta,
Vector<double>& r)
{
using namespace QuadTreeNames;
#ifdef WARN_ABOUT_SUBTLY_CHANGED_OOMPH_INTERFACES
// Warn about time argument being moved to the front
OomphLibWarning(
"Order of function arguments has changed between versions 0.8 and 0.85",
"FishDomain::macro_element_boundary(...)",
OOMPH_EXCEPTION_LOCATION);
#endif
// Which macro element?
// --------------------
switch (imacro)
{
// Macro element 0: Lower body
case 0:
// Which direction?
if (idirect == N)
{
FishDomain::r_lower_body_N(t, zeta, r);
}
else if (idirect == S)
{
FishDomain::r_lower_body_S(t, zeta, r);
}
else if (idirect == W)
{
FishDomain::r_lower_body_W(t, zeta, r);
}
else if (idirect == E)
{
FishDomain::r_lower_body_E(t, zeta, r);
}
else
{
std::ostringstream error_stream;
error_stream << "idirect is " << idirect << " not one of N, S, E, W"
<< std::endl;
throw OomphLibError(error_stream.str(),
OOMPH_CURRENT_FUNCTION,
OOMPH_EXCEPTION_LOCATION);
}
break;
// Macro element 1: Lower Fin
case 1:
// Which direction?
if (idirect == N)
{
FishDomain::r_lower_fin_N(t, zeta, r);
}
else if (idirect == S)
{
FishDomain::r_lower_fin_S(t, zeta, r);
}
else if (idirect == W)
{
FishDomain::r_lower_fin_W(t, zeta, r);
}
else if (idirect == E)
{
FishDomain::r_lower_fin_E(t, zeta, r);
}
else
{
std::ostringstream error_stream;
error_stream << "idirect is " << idirect << " not one of N, S, E, W"
<< std::endl;
throw OomphLibError(error_stream.str(),
OOMPH_CURRENT_FUNCTION,
OOMPH_EXCEPTION_LOCATION);
}
break;
// Macro element 2: Upper body
case 2:
// Which direction?
if (idirect == N)
{
FishDomain::r_upper_body_N(t, zeta, r);
}
else if (idirect == S)
{
FishDomain::r_upper_body_S(t, zeta, r);
}
else if (idirect == W)
{
FishDomain::r_upper_body_W(t, zeta, r);
}
else if (idirect == E)
{
FishDomain::r_upper_body_E(t, zeta, r);
}
else
{
std::ostringstream error_stream;
error_stream << "idirect is " << idirect << " not one of N, S, E, W"
<< std::endl;
throw OomphLibError(error_stream.str(),
OOMPH_CURRENT_FUNCTION,
OOMPH_EXCEPTION_LOCATION);
}
break;
// Macro element 3: Upper Fin
case 3:
// Which direction?
if (idirect == N)
{
FishDomain::r_upper_fin_N(t, zeta, r);
}
else if (idirect == S)
{
FishDomain::r_upper_fin_S(t, zeta, r);
}
else if (idirect == W)
{
FishDomain::r_upper_fin_W(t, zeta, r);
}
else if (idirect == E)
{
FishDomain::r_upper_fin_E(t, zeta, r);
}
else
{
std::ostringstream error_stream;
error_stream << "idirect is " << idirect << " not one of N, S, E, W"
<< std::endl;
throw OomphLibError(error_stream.str(),
OOMPH_CURRENT_FUNCTION,
OOMPH_EXCEPTION_LOCATION);
}
break;
default:
// Error
std::ostringstream error_stream;
error_stream << "Wrong imacro " << imacro << std::endl;
throw OomphLibError(
error_stream.str(), OOMPH_CURRENT_FUNCTION, OOMPH_EXCEPTION_LOCATION);
}
} // end of macro_element_boundary

Here are a few of the private member functions that define individual MacroElement boundaries:

  • The N[orthern] boundary of macro element 2 (which represents the upper body) coincides with the domain boundary that is parametrised by the geometric object pointed to by Back_pt. The function translates the coordinate $ \zeta \in [-1,1] $ to the Lagrangian coordinate $ \xi \in [\xi_{nose}, \xi_{tail}] $ along the geometric object. We use this Lagrangian coordinate to obtain the position vector to the domain boundary via a call to the GeomObject::position(...) function of the geometric object pointed to by Back_pt:
    //===============start_of_r_upper_body_N==============================
    /// Northern edge of upper body macro element; \f$ \zeta \in [-1,1] \f$
    //=====================================================================
    void FishDomain::r_upper_body_N(const unsigned& t,
    const Vector<double>& zeta,
    Vector<double>& r)
    {
    // Lagrangian coordinate along curved "back"
    Vector<double> x(1);
    x[0] = Xi_nose + (Xi_tail - Xi_nose) * 0.5 * (zeta[0] + 1.0);
    // Get position on curved back
    Back_pt->position(t, x, r);
    } // end of r_upper_body_N
  • The E[astern] boundary of macro element 2 is a straight vertical line from the "tail end" of the curved fish back to the x-axis:
    //================start_of_r_upper_body_E=============================
    /// Eastern edge of upper body macro element; \f$ \zeta \in [-1,1] \f$
    //=====================================================================
    void FishDomain::r_upper_body_E(const unsigned& t,
    const Vector<double>& zeta,
    Vector<double>& r)
    {
    // Top right corner (tail end) of body
    Vector<double> r_top(2);
    Vector<double> x(1);
    x[0] = Xi_tail;
    Back_pt->position(t, x, r_top);
    // Corresponding point on the x-axis
    Vector<double> r_back(2);
    r_back[0] = r_top[0];
    r_back[1] = 0.0;
    r[0] = r_back[0] + (r_top[0] - r_back[0]) * 0.5 * (zeta[0] + 1.0);
    r[1] = r_back[1] + (r_top[1] - r_back[1]) * 0.5 * (zeta[0] + 1.0);
    } // end of r_upper_body_E
  • The S[outhern] boundary of macro element 2 is a straight horizontal line from the "mouth" to the end of the body:
    //==================start_of_r_upper_body_S============================
    /// Southern edge of upper body macro element; \f$ \zeta \in [-1,1] \f$
    //=====================================================================
    void FishDomain::r_upper_body_S(const unsigned& t,
    const Vector<double>& zeta,
    Vector<double>& r)
    {
    // Top right (tail) corner of fish body
    Vector<double> r_top(2);
    Vector<double> x(1);
    x[0] = Xi_tail;
    Back_pt->position(t, x, r_top);
    // Straight line from mouth to start of fin (=end of body)
    r[0] = X_mouth + (r_top[0] - X_mouth) * 0.5 * (zeta[0] + 1.0);
    r[1] = 0.0;
    } // end of r_upper_body_S
  • The W[estern] boundary of macro element 2 is a straight line from the "mouth" to the "mouth" end of the curved upper boundary of the body:
    //===============start_of_r_upper_body_W==============================
    /// Western edge of upper body macro element; \f$ \zeta \in [-1,1] \f$
    //====================================================================
    void FishDomain::r_upper_body_W(const unsigned& t,
    const Vector<double>& zeta,
    Vector<double>& r)
    {
    // Top left (mouth) corner of curved boundary of upper body
    Vector<double> r_top(2);
    Vector<double> x(1);
    x[0] = Xi_nose;
    Back_pt->position(t, x, r_top);
    // The "mouth"
    Vector<double> r_mouth(2);
    r_mouth[0] = X_mouth;
    r_mouth[1] = 0.0;
    // Straight line from mouth to leftmost corner on curved boundary
    // of upper body
    r[0] = r_mouth[0] + (r_top[0] - r_mouth[0]) * 0.5 * (zeta[0] + 1.0);
    r[1] = r_mouth[1] + (r_top[1] - r_mouth[1]) * 0.5 * (zeta[0] + 1.0);
    } // end of r_upper_body_W
  • The S[outhern] boundary of macro element 0 (which represents the lower body) is simply a reflection of the N[orthern] boundary of macro element 2:
    /// Southern boundary of lower body macro element zeta \f$\in [-1,1] \f$
    void r_lower_body_S(const unsigned& t,
    const Vector<double>& zeta,
    Vector<double>& f)
    {
    // South of lower body is element is north of upper one.
    // Direction of the coordinate stays the same.
    r_upper_body_N(t, zeta, f);
    // Reflect vertical position
    f[1] = -f[1];
    }
  • etc.

Tedious? Yes! Rocket Science? No!

Further comments

Node updates in response to changes in the Domain shape.

You may have noticed that, even though we introduced MacroElements in the context of adaptive mesh refinement, the pointer to a refineable element's MacroElement is stored in the FiniteElement, rather than the (derived) RefineableElement class, suggesting that MacroElements have additional uses outside the context of mesh adaptation. Indeed, the code fragment that illustrated the use of Domains and MacroElements during mesh generation, was taken from the constructor of the non-refineable FishMesh, rather than its adaptive counterpart. During the mesh generation process, the FiniteElement's MacroElement representation was used to determine the position of its Nodes within the Domain. The same procedure can be employed to update the nodal positions in response to changes in the domain shape. This is implemented, generically, in the function

Mesh::node_update()

This function loops over all elements in a Mesh and updates their nodal positions in response to changes in the domain boundary. (If the Mesh's constituent elements's are not associated with MacroElements and if the Mesh does not implement the node update by other means, this function does not change the mesh.)

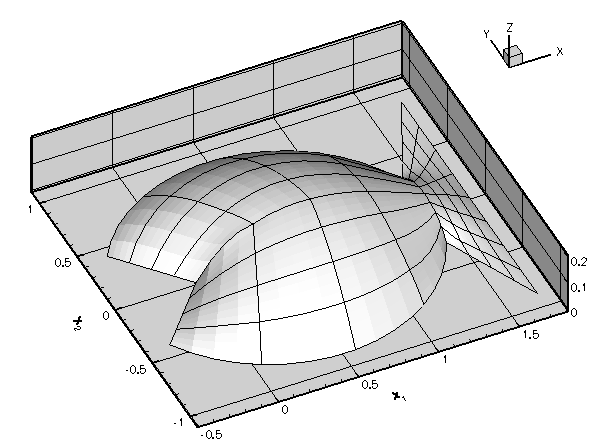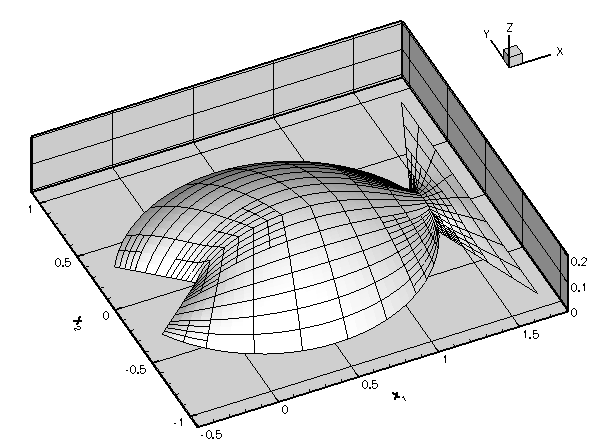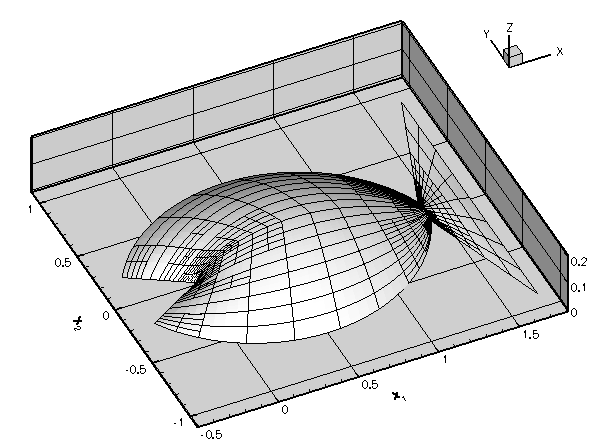
The following code fragment illustrates the trivial modifications to the driver code required to compute the solution of Poisson's equation in fish-shaped domain of various widths. We simply change the position of the GeomObject that specifies the curvilinear boundary (by changing the position of the circle's centre), call the Mesh::node_update() function, and recompute the solution.

//=================start_of_main==========================================
/// Demonstrate how to solve 2D Poisson problem in
/// fish-shaped domain with black-box mesh adaptation
/// and domain updates in response to changes in the domain
/// shape.
//========================================================================
int main()
{
//Set up the problem with 9 node refineable Poisson elements
RefineableFishPoissonProblem<RefineableQPoissonElement<2,3> > problem;
// Setup labels for output
//------------------------
DocInfo doc_info;
// Set output directory
doc_info.set_directory("RESLT");
// Adjust the domain shape by changing the width of the fish
//----------------------------------------------------------
unsigned nstep=3;
for (unsigned i=0;i<nstep;i++)
{
// Get pointer to GeomObject that defines the position of the
// fish's back:
GeomObject* fish_back_pt=problem.mesh_pt()->fish_back_pt();
// Recast to pointer to Circle object to get access to the member function
// that sets the y-position of the Circle's centre and decrease its
// value, making the fish narrower
dynamic_cast<Circle*>(fish_back_pt)->y_c()-=0.1;
// Update the domain shape in response to the changes in its
// boundary
problem.mesh_pt()->node_update();
// Solve the problem, allowing for up to two levels of refinement
problem.newton_solve(2);
//Output solution
problem.doc_solution(doc_info);
//Increment counter for solutions
doc_info.number()++;
}
} // end of main
RefineableFishPoissonProblem
Refineable Poisson problem in fish-shaped domain. Template parameter identifies the element type.
Definition: fish_poisson_adapt.cc:68
RefineableFishPoissonProblem::mesh_pt
RefineableFishMesh< ELEMENT > * mesh_pt()
Overloaded version of the problem's access function to the mesh. Recasts the pointer to the base Mesh...
Definition: fish_poisson_adapt.cc:87
RefineableFishPoissonProblem::doc_solution
void doc_solution(DocInfo &doc_info)
Doc the solution. Output directory and labels are specified by DocInfo object.
Definition: fish_poisson_adapt.cc:160
main
int main()
Demonstrate how to solve 2D Poisson problem in fish-shaped domain with black-box mesh adaptation and ...
Definition: fish_poisson_node_update.cc:197

The rest of the code remains unchanged. Here is a plot of the solution for various widths of the domain (computed with nine-node elements).

Adaptive solution of Poisson's equation in fish-shaped domains of varying width.

Good practice: Storing boundary coordinates

The above example demonstrated how the representation of curvilinear domain boundaries by GeomObjects allows oomph-lib's mesh generation and adaptation procedures to place nodes on these boundaries. We note that the Lagrangian coordinate(s) that parametrise(s) the relevant GeomObjects also provide a parametrisation of the corresponding domain boundaries. In certain applications (such as free-boundary or fluid-structure interaction problems) it is useful to have direct access to these boundary coordinates. For this purpose the Node class provides the function

Node::set_coordinates_on_boundary(const unsigned& b,
const Vector<double>& xi);

which allows the mesh writer to store the (vector of) boundary coordinates that a given (Boundary)Node is located at. The argument b specifies the number of the mesh boundary, reflecting the fact that nodes may be located on multiple domain boundaries, each of which is likely to have a different set of surface coordinates. [Note: The function is implemented as a broken virtual function in the Node base class. The actual functionality to store boundary coordinates is only provided in (and required by) the derived BoundaryNode class.]

Since the storage of boundary coordinates is optional, the Mesh base class provides a protected vector of bools,

std::vector<bool> Mesh::Boundary_coordinate_exists;

that indicates if the boundary coordinates have been stored for all Nodes on a specific mesh boundary. This vector is resized and its entries are initialised to false, when the number of mesh boundaries is declared with a call to Mesh::set_nboundary(...). If, during mesh refinement, a new BoundaryNode is created on the mesh's boundary b, its boundary coordinates are computed by interpolation from the corresponding values at the nodes in the father element, if Mesh::Boundary_coordinate_exists[b] has been set to true.

We regard it as good practice to set boundary coordinates for all BoundaryNodes that are located on curvlinear mesh boundaries. The source code fish_mesh.template.cc for the refineable FishMesh illustrates the methodology.

Source files for this tutorial

PDF file

A pdf version of this document is available.