This tutorial provides another quick demonstration of how to use unstructured meshes for the solution of fluid flow problems. (The xfig / Triangle tutorial already contains 2D and 3D unstructured fluid examples.)

The specific problem considered here serves as a "warm-up problem" for the corresponding fluid-structure interaction problem in which the part of the domain boundary is replaced by an elastic object.

The problem

Here is a sketch of the problem: Flow is driven through a 2D channel that is partly obstructed by an odd-shaped obstacle. The flow is driven by the imposed Poiseuille flow at the upstream end of the channel.

Sketch of the problem.

Mesh generation

We use the combination of xfig, oomph-lib's conversion code fig2poly , and the unstructured mesh generator Triangle to generate the mesh, using the procedure discussed in another tutorial.

We start by drawing the outline of the fluid domain as a polyline in xfig:

xfig drawing of the fluid body.

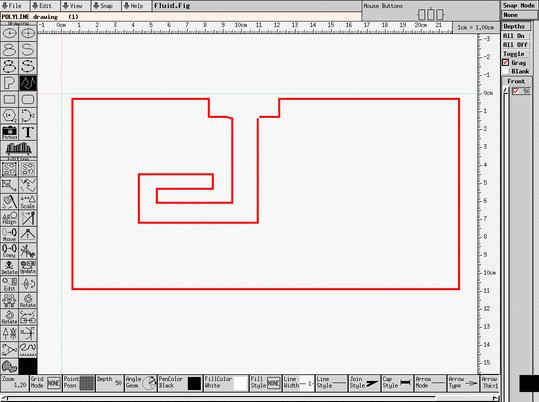
(Note that we draw the domain upside-down because of the way xfig orients its coordinate axes.)

We save the figure as a *.fig file and convert it to a *.poly file using oomph-lib's conversion code fig2poly (a copy of which is located in oomph-lib's bin directory):

fig2poly fluid.fig

This creates a file called fluid.fig.poly that can be processed using Triangle. For instance, to create a quality mesh with a maximum element size of 0.03 we use

triangle -q -a0.03 fluid.fig.poly

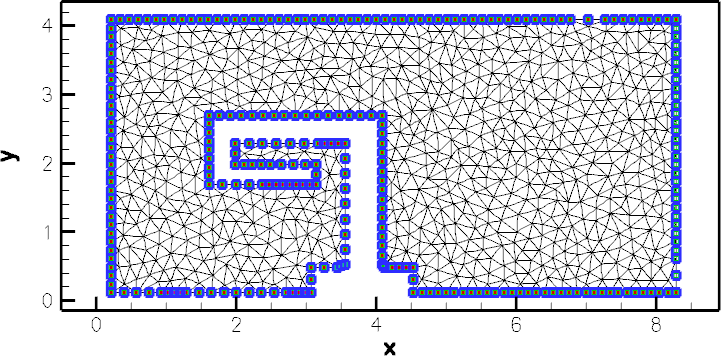
Here is a plot of the mesh, generated by showme distributed with Triangle :

Visualisation of the mesh with showme.

The *.poly, *.ele and *.node files generated by Triangle can now be used as input to oomph-lib's TriangleMesh class.

Results

The animation shown below illustrates the flow field (streamlines and pressure contours) for Reynolds numbers of An increase in Reynolds number increases the length of the recirculation region behind the obstacle; furthermore, the sharp corner at the "leading edge" of the obstacle creates very low pressures just downstream of the corner.

Flowfield (streamlines and pressure contours) at various Reynolds numbers.

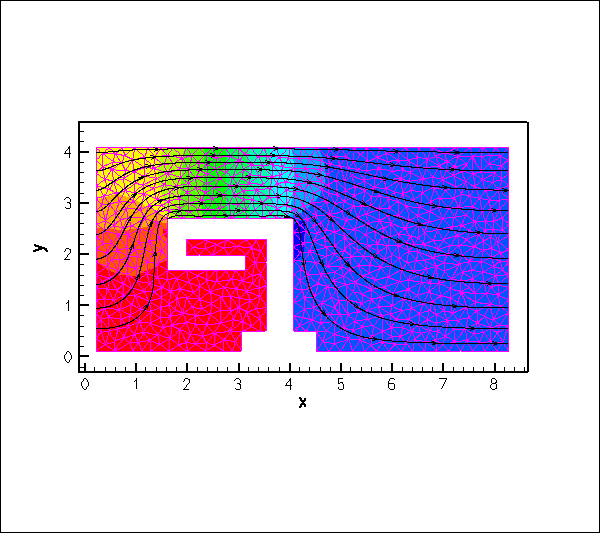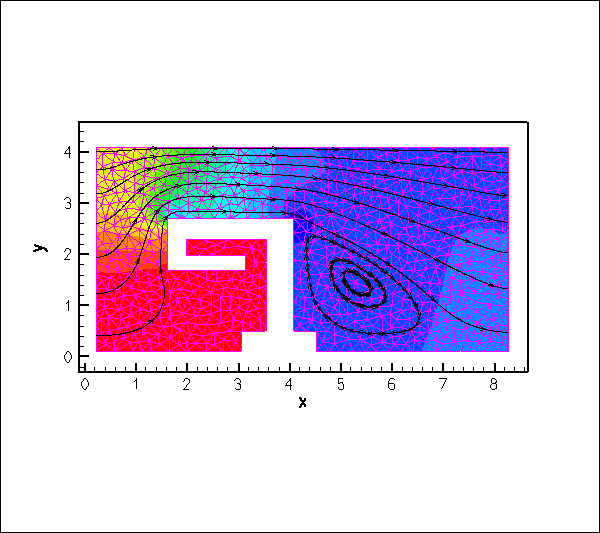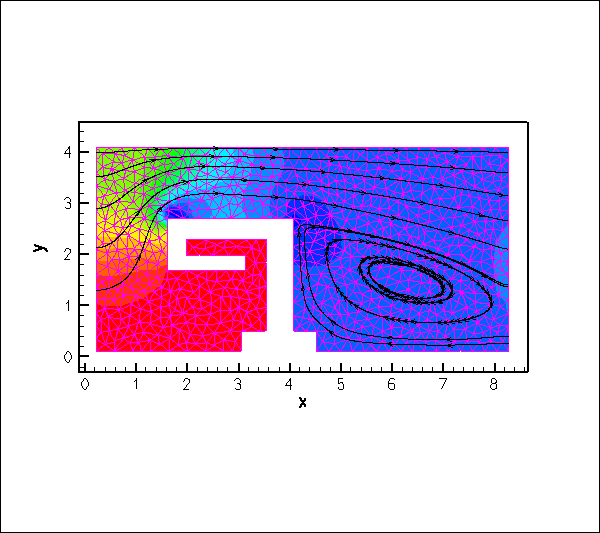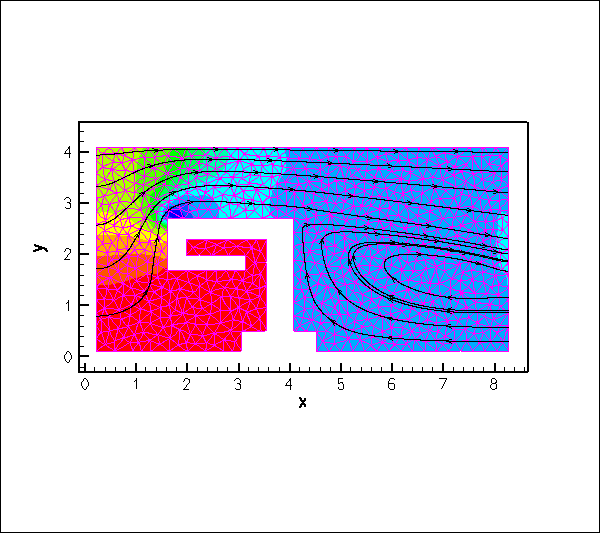
Creating the mesh

In anticipation of the mesh's use in a fluid-structure interaction problem, we create the mesh by multiple inheritance from oomph-lib's TriangleMesh and the SolidMesh base class. This will allow us to use pseudo-solid node-update techniques to update the position of the fluid nodes in response to changes in the domain boundary. In the present problem, the "elasticity" of the fluid elements plays no useful role; see Comments and Exercises for instructions on how to remove the pseudo-elasticity from the problem.

//===========start_mesh====================================================
/// Triangle-based mesh upgraded to become a (pseudo-) solid mesh
//=========================================================================
template<class ELEMENT>
class ElasticTriangleMesh : public virtual TriangleMesh<ELEMENT>,
                            public virtual SolidMesh 
{

The constructor calls the constructor of the underlying TriangleMesh, and, as usual, sets the Lagrangian coordinates to the current nodal positions, making the current configuration stress-free.

 
public:
 
 /// Constructor: 
 ElasticTriangleMesh(const std::string& node_file_name,
                     const std::string& element_file_name,
                     const std::string& poly_file_name,
                     TimeStepper* time_stepper_pt=
                     &Mesh::Default_TimeStepper) : 
 TriangleMesh<ELEMENT>(node_file_name,element_file_name,
                       poly_file_name, time_stepper_pt)
  {
   //Assign the Lagrangian coordinates
   set_lagrangian_nodal_coordinates();
   
   //Identify the domain boundaries
   this->identify_boundaries();
  }

The TriangleMesh constructor associates each polyline in the xfig drawing with a distinct oomph-lib mesh boundary. Hence the boundary nodes are initially located on the same, single boundary. The boundary conditions can be more easily applied if the boundary is divided into three boundaries, which is the task of the function TriangleMesh::identify_boundaries().

We first allocate storage for three boundaries:

 
 
 /// Function used to identify the domain boundaries
 void identify_boundaries()
  {
   // We will have three boundaries
   this->set_nboundary(3);

We loop over all nodes in the mesh and identify nodes on the left (inflow) boundary by their x-coordinate. We remove the node from the boundary 0 and re-allocate it to the new boundary 1:

 
   unsigned n_node=this->nnode();
   for (unsigned j=0;j<n_node;j++)
    {
     Node* nod_pt=this->node_pt(j);
 
     // Boundary 1 is left (inflow) boundary
     if (nod_pt->x(0)<0.226)
      {
       // If it's not on the upper or lower channel walls remove it
       // from boundary 0
       if ((nod_pt->x(1)<4.08)&&(nod_pt->x(1)>0.113))
        {
         this->remove_boundary_node(0,nod_pt);
        }

Similarly, we identify all nodes on the right (outflow) boundary and re-assign them to boundary 2, before re-generating the various boundary lookup schemes that identify which elements are located next to the various mesh boundaries:

       this->add_boundary_node(1,nod_pt);
      }
 
     // Boundary 2 is right (outflow) boundary
     if (nod_pt->x(0)>8.28)
      {
       // If it's not on the upper or lower channel walls remove it
       // from boundary 0
       if ((nod_pt->x(1)<4.08)&&(nod_pt->x(1)>0.113))
        {
         this->remove_boundary_node(0,nod_pt);
        }
       this->add_boundary_node(2,nod_pt);
      }
    }
   this->setup_boundary_element_info();
  }
 
 /// Empty Destructor
 virtual ~ElasticTriangleMesh() { }
 
 
};

Problem Parameters

As usual we define the various problem parameters in a global namespace. We define the Reynolds number and prepare a pointer to a constitutive equation (for the pseudo-elastic elements).

//==start_namespace==============================
/// Namespace for physical parameters
//==================================================
namespace Global_Physical_Variables
{
 
 /// Reynolds number
 double Re=0.0; 
 
 /// Pseudo-solid Poisson ratio
 double Nu=0.3;
 
 /// Constitutive law used to determine the mesh deformation
 ConstitutiveLaw *Constitutive_law_pt=0;
 
} // end_of_namespace

The driver code

We specify an output directory and instantiate a constitutive equation for the pseudo-elasticity, specifying the Poisson ratio.

//==start_of_main======================================================
/// Driver for unstructured fluid test problem
//=====================================================================
int main()
{
 // Label for output
 DocInfo doc_info;
 
 //Set the constitutive law for the pseudo-elasticity
 Global_Physical_Variables::Constitutive_law_pt = 
  new GeneralisedHookean(&Global_Physical_Variables::Nu);

We create the Problem object and output the domain boundaries and the initial guess for the flow field.

  // Build the problem with TTaylorHoodElements
  UnstructuredFluidProblem<PseudoSolidNodeUpdateElement<
   TTaylorHoodElement<2>, 
   TPVDElement<2,3> > > problem;
  
  // Output boundaries 
  problem.fluid_mesh_pt()->output_boundaries("RESLT_TH/boundaries.dat");
  
  // Output the initial guess for the solution
  problem.doc_solution(doc_info);
  doc_info.number()++;

Finally, we perform a straightforward parameter study by slowly increasing the Reynolds number of the flow from zero.

  
  // Parameter study
  double re_increment=5.0;
  unsigned nstep=2; // 10;
  for (unsigned i=0;i<nstep;i++)
   {
    // Solve the problem
    problem.newton_solve();
    
    // Output the solution
    problem.doc_solution(doc_info);
    doc_info.number()++;
    
    // Bump up Re
    Global_Physical_Variables::Re+=re_increment;
   }  //end_of_parameter_study

The Problem class

The Problem class has the usual member functions and provides explicit storage for the fluid mesh. [This is again slight overkill for the problem at hand, and is done mainly in anticipation of the "upgrade" of this driver code to the FSI problem with its multiple meshes; in the present problem we could, of course, store the pointer to the problem's one-and-only mesh directly in Problem::mesh_pt(). ]

//==start_of_problem_class============================================
/// Unstructured fluid problem
//====================================================================
template<class ELEMENT>
class UnstructuredFluidProblem : public Problem
{
 
public:
 
 /// Constructor 
 UnstructuredFluidProblem();
 
 /// Destructor (empty)
 ~UnstructuredFluidProblem(){}
 
 /// Access function for the fluid mesh
 ElasticTriangleMesh<ELEMENT>*& fluid_mesh_pt() 
  {
   return Fluid_mesh_pt;
  }
 
 /// Set the boundary conditions
 void set_boundary_conditions();
 
 /// Doc the solution
 void doc_solution(DocInfo& doc_info);
 
private:
 
 /// Fluid mesh
 ElasticTriangleMesh<ELEMENT>* Fluid_mesh_pt;
 
 
}; // end_of_problem_class

The Problem constructor

We start by building the fluid mesh, using the files created by Triangle .

//==start_constructor=====================================================
/// Constructor 
//========================================================================
template<class ELEMENT>
UnstructuredFluidProblem<ELEMENT>::UnstructuredFluidProblem()
{ 
 
 //Create fluid mesh
 string fluid_node_file_name="fluid.fig.1.node";
 string fluid_element_file_name="fluid.fig.1.ele";
 string fluid_poly_file_name="fluid.fig.1.poly"; 
 Fluid_mesh_pt = new ElasticTriangleMesh<ELEMENT>(fluid_node_file_name,
                                                  fluid_element_file_name,
                                                  fluid_poly_file_name);

Next, we apply the boundary conditions for the fluid and the pseudo-solid equations using the function set_boundary_conditions(), which also completes the build of the elements by setting the appropriate pointers to the physical variables.

 
 //Set the boundary conditions
 this->set_boundary_conditions();

We add the fluid mesh as a single sub-mesh to the Problem and build the global mesh (see the comment in The Problem class .)

 
 // Add fluid mesh
 add_sub_mesh(fluid_mesh_pt());
 
 // Build global mesh
 build_global_mesh();

Finally, we assign the equation numbers

 
 // Setup equation numbering scheme
 cout <<"Number of equations: " << assign_eqn_numbers() << std::endl; 
 
} // end_of_constructor

Setting the boundary conditions

We pin the pseudo-solid nodes along all domain boundaries, apply a no-slip condition for the fluid velocity along the solid boundary (boundary 0), pin the velocity at the inflow (boundary 1, where we will impose a Poiseuille flow profile), and impose parallel outflow at the downstream end (boundary 2). Given that the manual identification of mesh boundaries in unstructured meshes that are generated by third-party mesh generators is a relatively error-prone process, we document the boundary conditions in three separate files to allow an external sanity check; see the comments in the corresponding solid mechanics tutorial. The Comments and Exercises section of the present tutorial also has a sub-section that illustrates what can go wrong.

 
 
 
//============start_of_set_boundary_conditions=============================
/// Set the boundary conditions for the problem and document the boundary
/// nodes
//==========================================================================
template<class ELEMENT>
void UnstructuredFluidProblem<ELEMENT>::set_boundary_conditions()
{ 
 // Doc pinned nodes
 std::ofstream solid_bc_file("pinned_solid_nodes.dat");
 std::ofstream u_bc_file("pinned_u_nodes.dat");
 std::ofstream v_bc_file("pinned_v_nodes.dat");
 
 // Set the boundary conditions for fluid problem: All nodes are
 // free by default -- just pin the ones that have Dirichlet conditions
 // here. 
 unsigned nbound=Fluid_mesh_pt->nboundary();
 for(unsigned ibound=0;ibound<nbound;ibound++)
  {
   unsigned num_nod=Fluid_mesh_pt->nboundary_node(ibound);
   for (unsigned inod=0;inod<num_nod;inod++)
    {
     // Get node
     Node* nod_pt=Fluid_mesh_pt->boundary_node_pt(ibound,inod);
 
     // Pin velocity everywhere apart from outlet where we
     // have parallel outflow
     if (ibound!=2)
      {
       // Pin it
       nod_pt->pin(0);
       // Doc it as pinned
       u_bc_file << nod_pt->x(0) << " " << nod_pt->x(1) << std::endl;
      }
     // Pin it
     nod_pt->pin(1);
     // Doc it as pinned
     v_bc_file << nod_pt->x(0) << " " << nod_pt->x(1) << std::endl;
     
     // Pin pseudo-solid positions everywhere
     for(unsigned i=0;i<2;i++)
      {
       // Pin the node
       SolidNode* nod_pt=Fluid_mesh_pt->boundary_node_pt(ibound,inod);
       nod_pt->pin_position(i);
       
       // Doc it as pinned
       solid_bc_file << nod_pt->x(i) << " ";
      }
     solid_bc_file << std::endl;    
    }
  } // end loop over boundaries
 
 // Close
 solid_bc_file.close();

We complete the build of the elements by specifying the Reynolds number and the constitutive equation for the pseudo-solid equations.

 
 // Complete the build of all elements so they are fully functional
 unsigned n_element = fluid_mesh_pt()->nelement();
 for(unsigned e=0;e<n_element;e++)
  {
   // Upcast from GeneralisedElement to the present element
   ELEMENT* el_pt = dynamic_cast<ELEMENT*>(fluid_mesh_pt()->element_pt(e));
 
   //Set the Reynolds number
   el_pt->re_pt() = &Global_Physical_Variables::Re;
 
   // Set the constitutive law
   el_pt->constitutive_law_pt() =
    Global_Physical_Variables::Constitutive_law_pt;
  } 

Finally, we impose a Poiseuille profile at the inflow boundary (boundary 1).

 
 
 // Apply fluid boundary conditions: Poiseuille at inflow
 //------------------------------------------------------
 
 // Find max. and min y-coordinate at inflow
 unsigned ibound=1;
 //Initialise y_min and y_max to y-coordinate of first node on boundary
 double y_min=fluid_mesh_pt()->boundary_node_pt(ibound,0)->x(1);
 double y_max=y_min;
 //Loop over the rest of the nodes
 unsigned num_nod= fluid_mesh_pt()->nboundary_node(ibound);
 for (unsigned inod=1;inod<num_nod;inod++)
  {
   double y=fluid_mesh_pt()->boundary_node_pt(ibound,inod)->x(1);
   if (y>y_max)
    {
     y_max=y;
    }
   if (y<y_min)
    {
     y_min=y;
    }
  }
 double y_mid=0.5*(y_min+y_max);
 
 // Loop over all boundaries
 for (unsigned ibound=0;ibound<fluid_mesh_pt()->nboundary();ibound++)
  {
   unsigned num_nod= fluid_mesh_pt()->nboundary_node(ibound);
   for (unsigned inod=0;inod<num_nod;inod++)
    {
     // Parabolic inflow at the left boundary (boundary 1)
     if (ibound==1)
      {
       double y=fluid_mesh_pt()->boundary_node_pt(ibound,inod)->x(1);
       double veloc=1.5/(y_max-y_min)*
        (y-y_min)*(y_max-y)/((y_mid-y_min)*(y_max-y_mid));
       fluid_mesh_pt()->boundary_node_pt(ibound,inod)->set_value(0,veloc);
       fluid_mesh_pt()->boundary_node_pt(ibound,inod)->set_value(1,0.0);
      }
     // Zero flow elsewhere apart from x-velocity on outflow boundary
     else
      {
       if(ibound!=2)
        {
         fluid_mesh_pt()->boundary_node_pt(ibound,inod)->set_value(0,0.0);
        }
       fluid_mesh_pt()->boundary_node_pt(ibound,inod)->set_value(1,0.0);
      }
    }
  }
} // end_of_set_boundary_conditions

Post-processing

The post-processing routine outputs the flow field.

 
 
 
 
//==start_of_doc_solution=================================================
/// Doc the solution
//========================================================================
template<class ELEMENT>
void UnstructuredFluidProblem<ELEMENT>::doc_solution(DocInfo& doc_info)
{ 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned npts;
 npts=5; 
 
 // Output solution 
 sprintf(filename,"%s/soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 fluid_mesh_pt()->output(some_file,npts);
 some_file.close();
} //end_of_doc_solution

Comments and Exercises

What is the Reynolds number?

The problem considered here is a "toy"-problem, devised to illustrate the use of unstructured meshes in fluids problems. The specific non-dimensionalisation and parameter values are therefore of secondary importance. However, since oomph-lib's implementation of the Navier-Stokes equations is based on their non-dimensional form it is important to clarify the meaning of the Reynolds number in the present problem.

Recall that the Reynolds number is defined as

$Re = \frac{\rho {\cal U} {\cal L}}{\mu}$

where $\rho$ and $\mu$ are the fluid density and viscosity, respectively. ${\cal L}$ is the reference length chosen for the non-dimensionalisation of the coordinates. In the present problem, where the domain boundaries were simply drawn in xfig , no specific reference length was identified, but inspection of the maximum and minimum y-coordinates of the inflow boundary in the mesh plot shows that the inflow boundary has a (dimensional) length of $(4.0875 - 0.1125) {\cal L} = 3.975 {\cal L}.$ In the non-dimensional version of the Navier-Stokes equations, all velocities are non-dimensionalised with a reference velocity ${\cal U}$ . When we applied the inflow boundary conditions, we chose the (dimensionless) inflow profile such that its integral over the inflow boundary yields a value of 1. The velocity scale ${\cal U}$ may therefore be interpreted as a (dimensional) average inflow velocity through the channel, i.e. the volume flux divided by the reference length scale.

Setting the boundary conditions

We wish to re-iterate the comments made in the corresponding solid mechanics tutorial that the manual identification of nodes on domain boundaries is tedious and therefore error prone. It pays off to be as a paranoid as possible, by always documenting the domain boundaries and the applied boundary conditions.

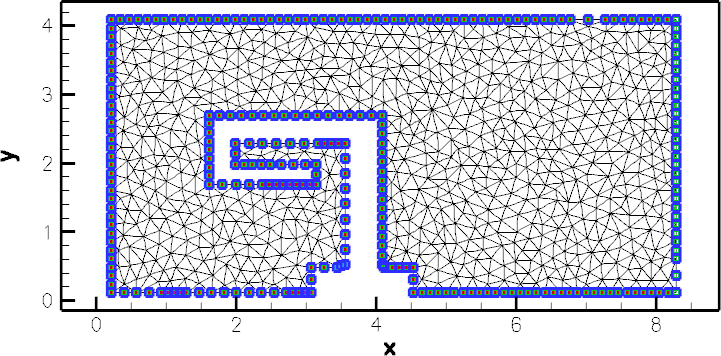
Here is the plot of boundary conditions applied in the present problem. Hollow blue markers indicate (pseudo-)solid boundary conditions (both displacements are pinned); small red markers identify nodes where the vertical fluid velocity is pinned; hollow green markers (filling the space between the blue and red lines markers) identify nodes at which the horizontal fluid velocity is pinned.

Plot of the correct boundary conditions.

Here is another plot, obtained with the initial version of our driver code – can you spot what's wrong and can you identify the lines were added to the mesh constructor to fix the problem?

Plot of the wrong boundary conditions.

Pseudo-elasticity

As mentioned above, the elements' pseudo-elasticity plays no useful role in the present problem, as the domain boundaries remain at fixed positions and no mesh movement is required.

As an exercise, remove all functionality related to the pseudo-elasticity by changing the element type from
PseudoSolidNodeUpdateElement<TTaylorHoodElement<2>,TPVDElement<2,3> >

to
TTaylorHoodElement<2>

Adjust the code as required (e.g. remove mesh's inheritance from the SolidMesh base class; remove the application of boundary conditions for the nodal positions; etc) and confirm that the results for the flow field remain unchanged.
Alternatively, the pseudo-elasticity can can be suppressed by pinning all nodal positions, drastically reducing the number of degrees of freedom in the problem without the need to rewrite the rest of the code. (Note that this is also a useful test for the development of FSI codes.)
However, if the pseudo-elastic capabilities are retained the fluid mesh can indeed deform as an elastic body; for example, by specifying a (solid mechanics) body force. Simply follow the steps used in the corresponding solid mechanics problem. Define the body force in the namespace Global_Physical_Variables and pass a (function-)pointer to it to the elements. N.B. The body force for the (pseudo-)solid equations must be specified explicitly because the Navier-Stokes equations have their own body force pointer! The compiler will complain about ambiguities in the following code:

[...]

//Set the body force

el_pt->body_force_fct_pt() = Global_Physical_Variables::gravity;

[...]

Instead, we must be more specific by writing

[...]

//Set the body force

el_pt->PVDEquationsBase<2>::body_force_fct_pt() =

Global_Physical_Variables::gravity;

[...]

indicating that it is the body force defined in the 2D solid mechanics equations that is being specified.

Source files for this tutorial

The source files for this tutorial are located in the directory:

demo_drivers/navier_stokes/unstructured_fluid/
The driver code is:

demo_drivers/navier_stokes/unstructured_fluid/unstructured_two_d_fluid.cc

PDF file

A pdf version of this document is available.