This is a slightly more advanced example in which we demonstrate the use of spatial adaptivity in time-dependent problems. We discuss the implementation of the spatially adaptive version of oomph-lib's unsteady Newton solver, Problem::unsteady_newton_solve(...), and explain why the assignment of initial conditions should be performed by overloading the Problem::set_initial_condition() function. We also discuss briefly how oomph-lib's generic dump and restart functions deal with adaptive meshes.

For this purpose consider the following problem:

The two-dimensional unsteady heat equation with flux boundary conditions in a quarter circle domain Solve

$\sum_{i=1}^2\frac{\partial^2 u}{\partial x_i^2} = \frac{\partial u}{\partial t} + f\left(x_1,x_2,t\right), \ \ \ \ \ \ \ \ \ \ (1)$

in the quarter-circle domain

, bounded by the coordinate axes and the unit circle, subject to Neumann boundary conditions,

$\left. \frac{\partial u}{\partial n}\right|_{\partial D_{Neumann}}= - \left. \frac{\partial u}{\partial x_2}\right|_{\partial D_{Neumann}}= g_0, \ \ \ \ \ \ \ \ \ \ (2)$

along the horizontal domain boundary $\partial D_{Neumann} = \{ (x_1,x_2) | x_1 \in [0,1], x_2=0 \}$ , and to Dirichlet boundary conditions,

$\left. u\right|_{\partial D_{Dirichlet}}=h_0, \ \ \ \ \ \ \ \ \ \ (3)$

elsewhere.

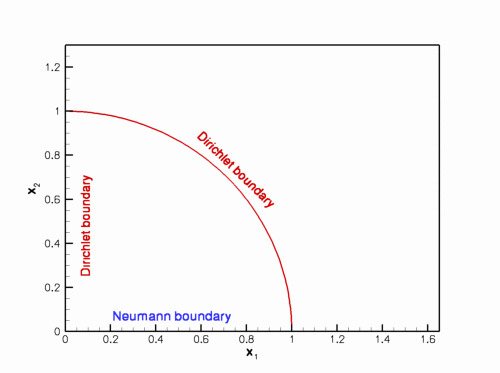
Sketch of the domain and the boundary conditions.

The initial conditions are given by

$u(x_1,x_2,t=0)=k_0(x_1,x_2), \ \ \ \ \ \ \ \ \ \ (4)$

where the functions $f, g_0, \ h_0$ and

are given.

We choose the functions $f, g_0, \ h_0$ and so that

$u_0(x_1,x_2,t) = \tanh\bigg[1-\alpha\bigg(\tan\Phi \big(x_1-\beta\tanh[ \gamma\cos\left(2\pi t\right)]\big)- x_2\bigg)\bigg] \ \ \ \ \ \ \ \ \ \ (5)$

is the exact solution.

The solution represents the "usual" tanh profile, whose steepness is controlled by the parameter $\alpha$ so that for $\alpha \gg 1$ the solution approaches a step. The step is oriented at an angle $\Phi$ against the axis and its position varies periodically. The parameter $\beta$ controls the amplitude of the step's lateral displacement, while $\gamma$ determines the rate at which its position changes. For $\gamma \gg 1$ , the step remains stationary for most of the period and then translates rapidly parallel to the axis, making this a very challenging problem.

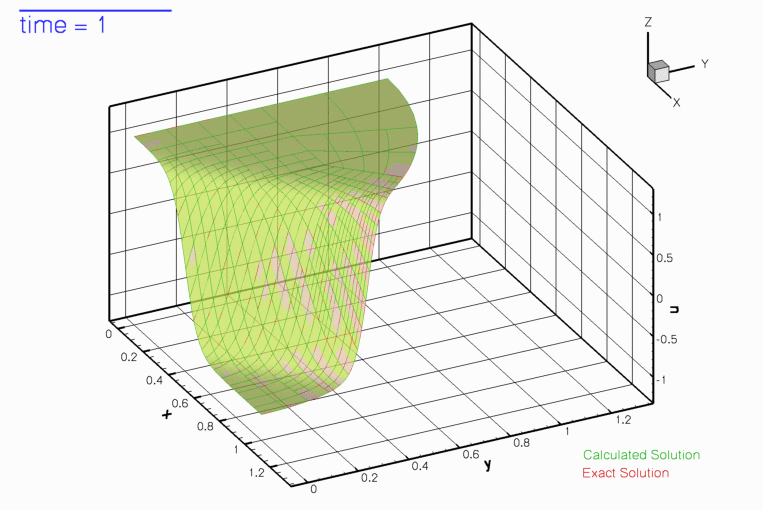
The figure below shows a snapshot of the animated solution, obtained from the spatially adaptive simulation discussed below, for the parameter values $\alpha=10, \ \Phi=45^o, \ \beta=0.3, \ \gamma=5.$

Snapshot of the solution.

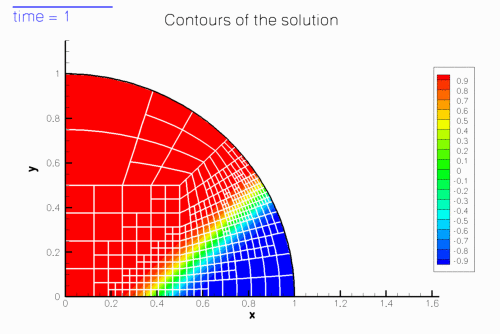
The mesh adaptation in response to the translation of the step can be seen more clearly in this contour plot, taken from another animation of the solution.

Contour plot of the solution.

Background: Spatial adaptivity in time-dependent problems

Enabling spatial adaptivity in time-dependent problems involves essentially the same steps as for steady problems:

The domain must be discretised with a mesh that is derived from the RefineableMesh base class.
An ErrorEstimator object must be created and passed to the mesh.
The empty virtual functions Problem::actions_before_adapt() and Problem::actions_after_adapt() may be overloaded to perform any actions that are required before or after the mesh adaptation, such as the deletion or recreation of any FaceElements that apply flux boundary conditions.

Once these steps have been performed, a spatially adaptive solution can be computed with a three-argument version of oomph-lib's unsteady Newton solver Problem::unsteady_newton_solve(...):

Problem::unsteady_newton_solve(dt,max_adapt,first)

The arguments to this function are as follows:

The double dt specifies the (fixed) timestep.
The unsigned max_adapt specifies the maximum number of spatial adaptations allowed.
The bool first indicates if the first timestep is performed. This argument is required to allow the automatic re-assignment of the initial conditions following any mesh adaptations during the computation of the first timestep.

Given these arguments, the unsteady Newton solver solves the non-linear system of spatially and temporally discretised equations to advance the solution from time to . Once the solution at time has been obtained, error estimates are computed for all elements. If any elemental error estimates are outside the target range, the solution is rejected and the mesh is adapted. In the course of mesh adaptation the existing solution (the nodal values and the history values) at time are interpolated onto the new mesh before recomputing the solution. This process is repeated until the error estimates are within the target range, or until the maximum number of adaptations, specified by the parameter max_adapt, is exceeded, just as in the steady case.

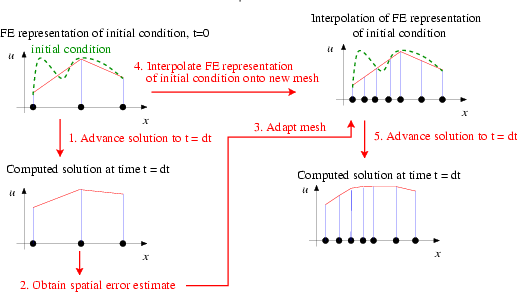
Here is an illustration of the procedure for a 1D problem:

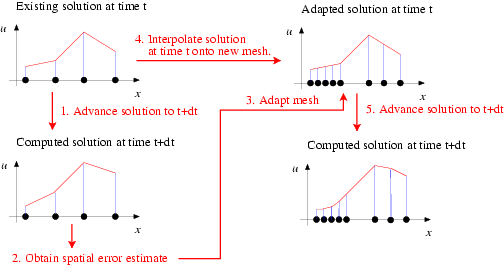
Sketch of the mesh adaptation for time-dependent problems.

This procedure is the obvious generalisation of the procedure for steady problems. However, in time-dependent problems two additional issues arise:

In a steady problem the interpolation of the solution onto the adapted mesh (step 4 in the above sketch) merely serves to provide an initial guess for the solution on the refined mesh. It is irrelevant if the interpolation from the coarse mesh provides a poor approximation of the actual solution as the solution is completely recomputed anyway.

In an unsteady problem, we also have to interpolate the history values (the solution at previous timesteps in a BDF scheme) onto the adapted mesh. Their values are not changed when the solution is advanced from time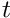 to 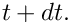In time-dependent problems, the benefit of repeated mesh adaptations (i.e. max_adapt > 1) is therefore limited by the fact that mesh refinement cannot improve their accuracy – the history values are always given by the (possibly poor) approximations obtained by interpolation from the coarser mesh employed at the previous timestep. We therefore recommend limiting the number of spatial adaptations to max_adapt = 1. We stress that, in practice, this is not a serious restriction because the time-integration procedure will only provide (temporally) accurate results if the timestep dt is so small that the solution at time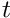 only differs slightly from that at time 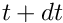. One level of mesh adaptation per timestep should therefore be sufficient to adapt the mesh in response to these changes.
The only exception to this recommendation arises during the computation of the first timestep, illustrated in the following sketch:

Sketch of the mesh adaptation during the computation of the first timestep.
When computing the first timestep, the solution on the initial mesh will have been created by assigning the nodal values according to the analytical initial condition (4). If the initial mesh is very coarse (as it should be), the finite-element representation of the initial condition is likely to be very poor, as shown in the above sketch. Clearly, the interpolation from the coarse onto the fine mesh cannot recover any small-scale features in the initial condition that were missed by its representation on the coarse mesh. It is therefore better to re-assign the initial condition (the values and the history values!) on the adapted mesh, as shown in this sketch:

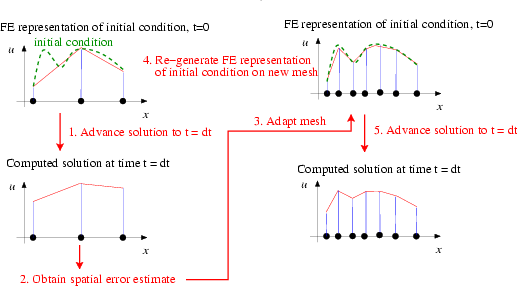Sketch of the modified mesh adaptation during the computation of the first timestep.
With this procedure, repeated mesh adaptations will improve the accuracy of the solution, therefore much larger values of max_adapt can (and should!) be specified when the first timestep is computed. The unsteady Newton solver Problem::unsteady_newton_solve(...) performs the revised procedure if the boolean argument first is set true. In that case, the values and history values on the adapted mesh are (re-)assigned by calling the function
Problem::set_initial_condition()

which is defined as an empty virtual function in the Problem base class. You should overload it in your derived Problem to ensure that your specific initial conditions are assigned by the mesh adaptation procedures. [In fact, the function Problem::set_initial_condition() is not quite empty – not re-setting the initial condition when performing mesh adaptations during the first timestep of a time-dependent simulation seems "so wrong" that the function issues a warning message. Although the overloading of this function is not strictly necessary if the initial conditions can be represented exactly by the interpolation from the coarse mesh onto the fine mesh, we consider it good practice to do so, for reasons discussed in another tutorial.]

Overview of the driver code

Equipped with this background information, the driver code for our example problem is easy to understand, if somewhat lengthy. [Using an example with Dirichlet boundary conditions along the entire domain boundary would have shortened the code significantly but we deliberately chose an example with Neumann boundary conditions to demonstrate that the functions Problem::actions_before_adapt() and Problem::actions_after_adapt() may be used exactly as in the steady computations.] We will not discuss the methodology for applying flux-type boundary conditions in problems with spatial adaptivity in detail, but refer to the discussion provided in the earlier steady example.

Overall, the code is a straightforward combination of the driver code for the steady Poisson problem with flux boundary conditions and spatial adaptivity and the driver code for the unsteady heat equation without spatial adaptivity.

Global parameters and functions

As usual, we store the problem parameters in a namespace, TanhSolnForUnsteadyHeat, in which we also specify the source function, the prescribed flux along the Neumann boundary and the exact solution.

Representing the curvilinear domain boundary by a GeomObject

As discussed elsewhere, oomph-lib's mesh adaptation procedures require curvilinear domain boundaries to be represented by GeomObjects which describe the object's shape via their member function GeomObject::position(...). This function exists in two versions:

The two-argument version, GeomObject::position(xi,r) computes the position vector, r, to the point on/in the GeomObject, parametrised by the vector of intrinsic coordinates, xi.
The three-argument version GeomObject::position(t,xi,r), where t is an unsigned, computes the position vector at the t - th previous timestep.

In the current problem, the domain boundary is stationary, therefore the steady and unsteady versions of the function are identical. Here is the complete source code for the MyUnitCircle object which we will use to represent the curvilinear domain boundary:

//============start_of_MyUnitCircle====================================
/// Unit circle as GeomObject
/// \f[ x = \cos(\xi)  \f]
/// \f[ y = \sin(\xi)  \f]
//=====================================================================
class MyUnitCircle : public GeomObject
{
 
public:
 
 /// Constructor: The circle is a 1D object
 /// (i.e. it's parametrised by one intrinsic coordinate) in 2D space.
 /// Pass these arguments to the constructor of the GeomObject base class.
 MyUnitCircle() : GeomObject(1,2) {}
 
 /// Destructor: Empty
 virtual ~MyUnitCircle() {}
 
 /// Current position vector to material point at 
 /// Lagrangian coordinate xi 
 void position(const Vector<double>& xi, Vector<double>& r) const
  {
   // Position vector
   r[0] = cos(xi[0]);
   r[1] = sin(xi[0]);
  } // end of position(...)
 
 
 /// Parametrised position on object: r(xi). Evaluated at
 /// previous time level. t=0: current time; t>0: previous
 /// time level. Circle is fixed -- simply call the steady version.
 void position(const unsigned& t, const Vector<double>& xi,
               Vector<double>& r) const
  {
   // Call steady version 
   position(xi,r);
  } // end of position(...)
 
 
}; // end of MyUnitCircle

The main function

As before, we use command line arguments to (optionally) specify a restart file. We store the command line arguments in the namespace CommandLineArgs and build the Problem object, passing the pointer to the source function. Next we specify the time-interval for the simulation and set the error targets for the spatial adaptation.

//======start_of_main=====================================================
/// Demonstrate how to solve an unsteady heat problem
/// with mesh adaptation. Command line arguments specify 
/// the name of the restart file. 
//========================================================================
int main(int argc, char* argv[])
{
 
 // Store command line arguments
 CommandLineArgs::setup(argc,argv);
 
 // Build problem
 RefineableUnsteadyHeatProblem<RefineableQUnsteadyHeatElement<2,3> >
  problem(&TanhSolnForUnsteadyHeat::get_source);
   
 // Specify duration of the simulation
 //double t_max=3.0;
 
 // Set targets for spatial adaptivity
 problem.bulk_mesh_pt()->max_permitted_error()=0.001;
 problem.bulk_mesh_pt()->min_permitted_error()=0.0001;

We create and initialise the boolean flag that indicates if the first timestep is computed, and choose a large initial value for the number of permitted mesh adaptations. We then assign the initial conditions on the coarse initial mesh and retrieve the timestep (chosen when the initial conditions are assigned in set_initial_condition() ) from the problem's Time object.

 // Set IC
 problem.set_initial_condition();
 
 // Initial timestep: Use the one used when setting up the initial
 // condition
 double dt=problem.time_pt()->dt();

If the simulation has been restarted, the first timestep is not the step at which the initial condition has to be assigned, therefore we reset the first and max_adapt parameters to their appropriate values. If the run is not restarted, the problem will have been built with a very coarse initial mesh (comprising just three elements). We don't need an error estimator to tell us that this is too coarse to represent the solution accurately and apply two levels of uniform refinement before solving the problem. Note that we refine the entire problem, not just the mesh to ensure that Problem::actions_before_adapt() and Problem::actions_after_adapt() are executed and the equation numbering scheme is re-generated. Problem::refine_uniformly() also interpolates the solution from the coarse initial mesh onto the refined mesh but, as discussed above, this will lead to a very poor representation of the initial condition. Therefore we re-assign the initial condition on the refined mesh and document the finite-element representation of the initial condition.

 // If restart: The first step isn't really the first step,
 // i.e. initial condition should not be re-set when 
 // adaptive refinement has been performed. Also, limit
 // the max. number of refinements per timestep to the
 // normal value straightaway.
 if (CommandLineArgs::Argc==2)
  {
   first=false;
   max_adapt=1;
  }
 // If no restart, refine mesh uniformly before we get started
 else
  {
   problem.refine_uniformly();
   problem.refine_uniformly();
   // Solution is automatically interpolated from the coarse initial mesh
   // onto the refined mesh but this provides a very poor representation
   // of the intial condition: Re-assign the initial conditions
   problem.set_initial_condition();
  }
 
 //Output FE representation of the initial condition
 problem.doc_solution();

The time-stepping loop itself is very similar to that used in the example without spatial adaptivity. Here we call the three-argument version of the unsteady Newton solver Problem::unsteady_newton_solve(...) and re-set the parameters max_adapt and first to their appropriate values once the first step has been performed.

 // Find number of steps
 unsigned nstep = 6; // unsigned(t_max/dt);
 
 // Timestepping loop
 for (unsigned istep=0;istep<nstep;istep++)
  {
   // Take timestep 
   problem.unsteady_newton_solve(dt,max_adapt,first);
   
   // Now we've done the first timestep -- don't re-set the IC
   // in subsequent steps
   first=false;
   
   // Reduce the number of spatial adaptations to one per 
   // timestep
   max_adapt=1;
   
   //Output solution
   problem.doc_solution();
 
  }
 
 
}; // end of main

The problem class

As discussed above, the problem class mainly contains verbatim copies of the member functions in the corresponding steady and unsteady problems:

//=====start_of_problem_class=========================================
/// Unsteady heat problem in quarter circle domain.
//====================================================================
template<class ELEMENT>
class RefineableUnsteadyHeatProblem : public Problem
{
 
public:
 
 /// Constructor: Pass pointer to source function
 RefineableUnsteadyHeatProblem(UnsteadyHeatEquations<2>::
                             UnsteadyHeatSourceFctPt source_fct_pt);
 
 /// Destructor: Close trace file
 ~RefineableUnsteadyHeatProblem();
 
 /// Update the problem specs after solve (empty)
 void actions_after_newton_solve(){}
 
 /// Update the problem specs before solve (empty)
 void actions_before_newton_solve(){}
 
 /// Update the problem specs after timestep (empty)
 void actions_after_implicit_timestep(){}
 
 /// Update the problem specs before next timestep: 
 /// Set Dirchlet boundary conditions from exact solution.
 void actions_before_implicit_timestep();
 
 /// Actions before adapt: Wipe the mesh of prescribed flux elements
 void actions_before_adapt();
 
 /// Actions after adapt: Rebuild the mesh of prescribed flux elements
 void actions_after_adapt();
 
 /// Set initial condition (incl previous timesteps) according
 /// to specified function. Note that his overloads the virtual
 /// function in the Problem base class and is therefore executed 
 /// automatically to re-assign the initial conditions during the 
 /// spatially adaptive solution at the first timestep.
 void set_initial_condition();
 
 /// Create UnsteadyHeat flux elements on boundary b of the Mesh pointed
 /// to by bulk_mesh_pt and add them to the Mesh object pointed to by 
 /// surface_mesh_pt
 void create_flux_elements(const unsigned &b, Mesh* const &bulk_mesh_pt,
                           Mesh* const &surface_mesh_pt);
 
 /// Delete UnsteadyHeat flux elements and wipe the surface mesh
 void delete_flux_elements(Mesh* const &surface_mesh_pt);
 
 /// Doc the solution
 void doc_solution();
 
 /// Dump problem data to allow for later restart
 void dump_it(ofstream& dump_file);
 
 /// Read problem data for restart
 void restart(ifstream& restart_file);
 
 /// Pointer to bulk mesh
 RefineableQuarterCircleSectorMesh<ELEMENT>* bulk_mesh_pt()
  {
   return Bulk_mesh_pt;
  }
 
 
private:
 
 /// Pointer to GeomObject that specifies the domain bondary
 GeomObject* Boundary_pt;
 
 /// Pointer to source function
 UnsteadyHeatEquations<2>::UnsteadyHeatSourceFctPt Source_fct_pt;
 
 /// Pointer to the "bulk" mesh
 RefineableQuarterCircleSectorMesh<ELEMENT>* Bulk_mesh_pt;
 
 /// Pointer to the "surface" mesh
 Mesh* Surface_mesh_pt;
 
 /// Pointer to central node (exists at all refinement levels) for doc
 Node* Doc_node_pt;
 
 /// Doc info object
 DocInfo Doc_info;
 
 /// Trace file
 ofstream Trace_file;
 
}; // end of problem_class

The problem constructor

The problem constructor combines the constructors of the steady and unsteady problems. We start by creating a DocInfo object to control the output, set the parameters for the exact solution and create the TimeStepper:

//========start_of_constructor============================================
/// Constructor for UnsteadyHeat problem in quarter circle domain.
/// Pass pointer to source function.
//========================================================================
template<class ELEMENT>
RefineableUnsteadyHeatProblem<ELEMENT>::RefineableUnsteadyHeatProblem(
   UnsteadyHeatEquations<2>::UnsteadyHeatSourceFctPt source_fct_pt) : 
         Source_fct_pt(source_fct_pt)
{ 
 
 
 // Setup labels for output
 //------------------------
 
 // Output directory
 Doc_info.set_directory("RESLT");
 
 // Output number
 Doc_info.number()=0; 
 
 // Open trace file
 char filename[100];   
 sprintf(filename,"%s/trace.dat",Doc_info.directory().c_str());
 Trace_file.open(filename);
 
 Trace_file << "VARIABLES=\"time t\",\"u<SUB>FE</SUB>\",\"u<SUB>exact</SUB>\","
            << "\"A\","
            << "\"X<SUB>step</SUB>\","
            << "\"N<SUB>element</SUB>\","
            << "\"N<SUB>refined</SUB>\","
            << "\"N<SUB>unrefined</SUB>\","
            << "\"norm of error\","
            << "\"norm of solution\""
            << std::endl;
 
 
 // Setup parameters for tanh solution
 // ----------------------------------
 
 // Steepness of step
 TanhSolnForUnsteadyHeat::Alpha=10.0;
 
 // Orientation of step
 TanhSolnForUnsteadyHeat::TanPhi=1.0;
 
 // Amplitude for movement of step
 TanhSolnForUnsteadyHeat::Beta=0.3; 
 
 // Parameter for time-dependence of step movement
 TanhSolnForUnsteadyHeat::Gamma=5.0;
 
 
 //Allocate the timestepper -- This constructs the time object as well
 add_time_stepper_pt(new BDF<2>());

We create the GeomObject that describes the curvilinear domain boundary and pass it to the mesh constructor:

 // Setup mesh
 //-----------
 
 // Build geometric object that forms the curvilinear domain boundary:
 // a unit circle 
 
 // Create GeomObject
 Boundary_pt=new MyUnitCircle;
 
 // Start and end coordinates of curvilinear domain boundary on circle
 double xi_lo=0.0;
 double xi_hi=MathematicalConstants::Pi/2.0;
 
 // Now create the bulk mesh. Separating line between the two 
 // elements next to the curvilinear boundary is located half-way
 // along the boundary.
 double fract_mid=0.5;
 Bulk_mesh_pt = new RefineableQuarterCircleSectorMesh<ELEMENT>(
  Boundary_pt,xi_lo,fract_mid,xi_hi,time_stepper_pt());

Next, we create the surface mesh that contains the prescribed flux elements and combine the two submeshes to the Problem's global mesh. We create an instance of the Z2ErrorEstimator and pass it to the bulk mesh.

 // Create the surface mesh as an empty mesh
 Surface_mesh_pt=new Mesh;
 
 // Create prescribed-flux elements from all elements that are 
 // adjacent to boundary 0 (the horizontal lower boundary), and add them 
 // to the (so far empty) surface mesh.
 create_flux_elements(0,Bulk_mesh_pt,Surface_mesh_pt);
 
 // Add the two sub meshes to the problem
 add_sub_mesh(Bulk_mesh_pt);
 add_sub_mesh(Surface_mesh_pt);
 
 // Combine all submeshes into a single global Mesh
 build_global_mesh();
 
 // Set error estimator for bulk mesh
 Z2ErrorEstimator* error_estimator_pt=new Z2ErrorEstimator;
 Bulk_mesh_pt->spatial_error_estimator_pt()=error_estimator_pt;

We pin the nodal values on the Dirichlet boundaries and select the central node in the unrefined three-element mesh as the control node at which the solution is documented in the trace file.

 // Set the boundary conditions for this problem: All nodes are
 // free by default -- just pin the ones that have Dirichlet conditions
 // here. 
 unsigned n_bound = Bulk_mesh_pt->nboundary();
 for(unsigned b=0;b<n_bound;b++)
  {
   // Leave nodes on boundary 0 free -- this is where we apply the flux
   // boundary condition
   if (b!=0)
    {
     unsigned n_node = Bulk_mesh_pt->nboundary_node(b);
     for (unsigned n=0;n<n_node;n++)
      {
       Bulk_mesh_pt->boundary_node_pt(b,n)->pin(0); 
      }
    }
  }
 
 // Extract pointer to the central node (this exists at all refinement levels)
 // for doc of solution
 FiniteElement* el0_pt=Bulk_mesh_pt->finite_element_pt(0);
 unsigned nnod=el0_pt->nnode();
 Doc_node_pt=el0_pt->node_pt(nnod-1);

Finally, we complete the build of all elements by passing the relevant function pointers to the elements, and assign the equation numbers.

 // Complete the build of all elements so they are fully functional
 //----------------------------------------------------------------
 
 // Find number of elements in mesh
 unsigned n_element = Bulk_mesh_pt->nelement();
 
 // Loop over the elements to set up element-specific 
 // things that cannot be handled by constructor
 for(unsigned i=0;i<n_element;i++)
  {
   // Upcast from FiniteElement to the present element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(Bulk_mesh_pt->element_pt(i));
 
   //Set the source function pointer
   el_pt->source_fct_pt() = Source_fct_pt;
  }
 
 // Loop over the flux elements to pass pointer to prescribed flux function
 n_element=Surface_mesh_pt->nelement();
 for(unsigned e=0;e<n_element;e++)
  {
   // Upcast from GeneralisedElement to UnsteadyHeat flux element
   UnsteadyHeatFluxElement<ELEMENT> *el_pt = 
    dynamic_cast<UnsteadyHeatFluxElement<ELEMENT>*>(
     Surface_mesh_pt->element_pt(e));
 
   // Set the pointer to the prescribed flux function
   el_pt->flux_fct_pt() = 
    &TanhSolnForUnsteadyHeat::prescribed_flux_on_fixed_y_boundary;
  }
 
 // Do equation numbering
 cout <<"Number of equations: " << assign_eqn_numbers() << std::endl; 
 
} // end of constructor

Other member functions

The remaining member functions

actions_after_newton_solve()
actions_before_newton_solve()
actions_after_implicit_timestep()
actions_before_implicit_timestep()
actions_before_adapt()
actions_after_adapt()
set_initial_condition()
create_flux_elements(...)
delete_flux_elements(...)
doc_solution()
dump_it(...)
restart(...)

are identical (or at least extremely similar) to those in previous examples, so we do not list them here. You can examine the functions in detail in the source code two_d_unsteady_heat_adapt.cc.

Dump/restart with spatial adaptivity

It is worth examining the dump and restart functions, however, as they demonstrate that the generic versions defined in the Problem base class can also deal with adaptive problems – a non-trivial task!

//=======start_of_dump_it=================================================
/// Dump the solution to disk
//========================================================================
template<class ELEMENT>
void RefineableUnsteadyHeatProblem<ELEMENT>::dump_it(ofstream& dump_file)
{
 // Dump the refinement pattern and the generic problem data
 Problem::dump(dump_file);
  
} // end of dump_it
 
//=========start_of_restart===============================================
/// Read solution from disk
//========================================================================
template<class ELEMENT>
void RefineableUnsteadyHeatProblem<ELEMENT>::restart(ifstream& restart_file)
{
 
 // Refine the mesh and read in the generic problem data
 Problem::read(restart_file);
 
} // end of restart

Since details of their implementation are hidden from the user, we briefly comment on the various tasks performed by these functions. The main task of the Problem::read(...) function is to read values (and history values) of all Data objects from a file and to assign these values to the appropriate Data (and Node) objects in the Problem. This assumes that the Problem's constituent Meshes, elements, Nodes and Data objects have been created, and that the Problem's various pointer-based lookup schemes access them in the order they were in when the Problem was dumped to the restart file. In a non-adaptive computation, the number of elements and the number of Data objects remain constant throughout the simulation and the Problem::read(...) function can be called as soon as the Problem has been built – usually by its constructor. (The Problem constructor always builds and enumerates its constituent objects in the same order.)

In a simulation with spatial adaptivity the number of elements, Nodes and Data objects varies throughout the computation. It is therefore necessary to re-generate the Problem's refinement pattern before the Data values can be read from the restart file. This is achieved (internally) by calling the function RefineableMesh::dump_refinement(...) for all refineable meshes before the Data is dumped. This function writes the Mesh's refinement pattern to the restart file, using a format that can be read by the corresponding member function RefineableMesh::refine(...) which adapts an unrefined mesh so that its topology and the order of its Nodes and elements is recreated.

Comments and exercises

The plots below show the time history of various parameters.

The upper graph compares the solution at the control node (red line) against the exact solution (green line).
The middle graph shows the position of the step by plotting its intercept with the axis as a function of time, and the error of the solution.
The lower graph illustrates the evolution of the adaptive spatial refinement process: The green line illustrates the total number of elements; the blue and red lines show the number of elements that are refined and unrefined at each timestep.

Time history of the solution.

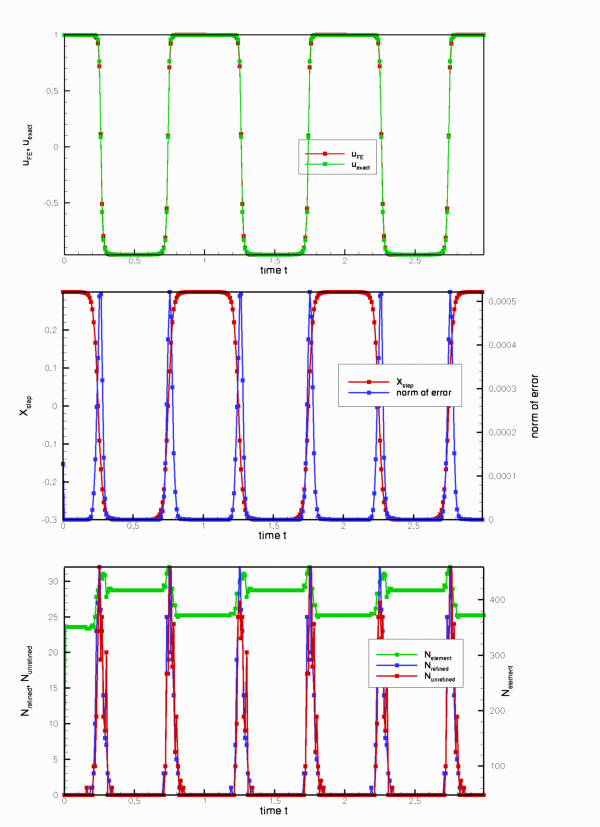
The plots illustrate clearly how the mesh is adapted as the step moves through the domain – the peaks in the number of refined/unrefined elements per timestep coincide with the periods during which the step moves very rapidly. The increase in the error during these phases is mainly due to the temporal error – the animation shows that the computed solution lags behind the exact one. We will address this by adding adaptive time-stepping in another example.

Exercises

Confirm that the error during the periods of rapid change in the solution is due to the temporal error by repeating the simulation with a smaller/larger timestep and/or a time-stepping scheme with higher/lower order (e.g. BDF<1> or BDF<4>).
Assess the importance of re-assigning the initial conditions when spatial adaptations are performed during the computation of the first timestep.
1. Compare the finite-element representation of the initial condition(contained in the file RESLT/soln0.dat) against that obtained when the re-assignment of the initial conditions after the two calls to problem.refine_uniformly() in the main function is suppressed.
2. Comment out the calls to problem.refine_uniformly() and set first=false throughout the main function and compare the computed results against those obtained with
  the correct procedure.

Source files for this tutorial

The source files for this tutorial are located in the directory: demo_drivers/unsteady_heat/two_d_unsteady_heat_adapt/
The driver code is: demo_drivers/unsteady_heat/two_d_unsteady_heat_adapt/two_d_unsteady_heat_adapt.cc

PDF file

A pdf version of this document is available.