Demo problem: Flow in a 2D channel with an oscillating wall revisited – AlgebraicElements: How to customise the mesh update

In many previous examples we illustrated how oomph-lib's Domain and MacroElement objects facilitate the generation of refineable (and non-refineable) meshes in domains with moving, curvilinear boundaries. Consult, for instance:

The two main features of the MacroElement/Domain - based node-update are that, once the curvilinear domain is represented by a Domain object

  1. Any subsequent mesh refinement will respect the curvilinear domain boundaries.

  2. The udate of the nodal positions in response to a change in the position of the domain's curvilinear boundaries may be performed by the "black-box" function Mesh::node_update().

The availability of a "black-box" node-update procedure is very convenient but in some applications it may be desirable (or even necessary) to provide a customised node-update function, either because the mesh deformation generated by the "black-box" procedure is not appropriate or because it is not efficient. The latter problem arises particularly in fluid-structure interaction problems.

In this tutorial we shall demonstrate an alternative node-update technique, based on oomph-lib's AlgebraicNode, AlgebraicElement, and AlgebraicMesh classes. The key feature of this approach is that it allows "each node to update its own position". This is in contrast to the Domain/MacroElement-based approach in which we can only update the nodal positions of all nodes in the mesh simultaneously – not a particularly sparse operation! [We note that the Node and FiniteElement base classes provide the virtual functions Node::node_update() and FiniteElement::node_update(). These functions are intended to be used for node-by-node or element-by-element node-updates but in their default implementations they are empty. Hence no node-update is performed unless these functions are overloaded in derived classes such as AlgebraicNode and AlgebraicElement.]

Overview

The idea behind the algebraic node-updates is simple: The AlgebraicMesh class (the base class for meshes containing AlgebraicElements and AlgebraicNodes) contains the pure virtual function

void AlgebraicMesh::algebraic_node_update(..., AlgebraicNode* node_pt)=0;

which must be implemented in every specific AlgebraicMesh. Its task is to update the position of the node specified by the pointer-valued argument.

The specific implementation of the node-update operation is obviously problem-dependent but it is easy to illustrate the general procedure by considering the collapsible channel mesh sketched below:

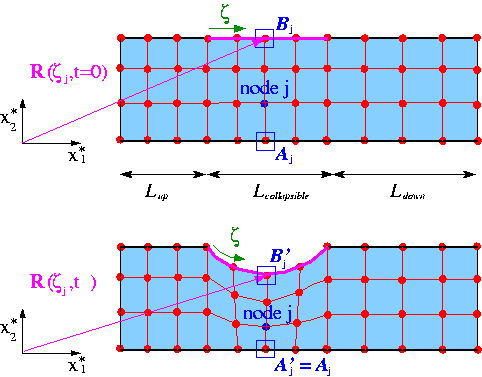
Sketch of the algebraic node-update procedure for the collapsible channel mesh.

The upper figure shows the mesh in the undeformed domain in which wall shape is parametrised by the intrinsic (Lagrangian) coordinate $ \zeta $ as $ {\bf R}(\zeta,t=0) = (L_{up} + \zeta, 1) ^T. $ In this configuration each node is located at a certain fraction along the vertical lines across the channel. For instance, the $ j$-th node (drawn in blue) is located at a fraction of $ \omega_j = 1/3 $ along the straight line that connects reference point $ {\bf A}_j $ on the bottom wall to reference point $ {\bf B}_j $ on the flexible upper wall. We note that reference point $ {\bf B}_j $ may be identified by its Lagrangian coordinate $ \zeta_j $ on the wall.

The lower figure shows a sketch of the deformed domain and illustrates a possible algebraic node-update strategy: Given the new wall shape, described by $ {\bf R}(\zeta,t) $, we position each node on the straight line that connects its reference point $ {\bf A}'_j = {\bf A}_j $ on the lower wall to the reference point $ {\bf B}'_j = {\bf R}(\zeta_j,t) $ on the deformable upper wall.

To perform this node-update procedure for a specific node, we generally have to store

  • A pointer to one (or more) GeomObject(s) that define the curvilinear domain boundaries.

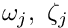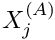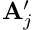  • A number of node-specific reference values (such as $ \omega_j, \ \zeta_j $, and the $ x_1 $ -coordinate of point $ {\bf A}_j $, $ X^{(A)}_j $, say) that establish the node's position relative to these GeomObjects.

  • A pointer to the AlgebraicMesh that implements the node-update procedure.

Since the node-update data is node-specific, we provide storage for it in the AlgebraicNode class – a class that is derived from the Node class. The node-update function itself is shared by many nodes in the mesh and is implemented in AlgebraicMesh::algebraic_node_update(...). This function extracts the node-update parameters, $ \omega_j, \ \zeta_j $, and $ X^{(A)}_j $ and the pointer to the GeomObject that parametrises the wall, wall_pt, say, from the AlgebraicNode passed to it. With these parameters, the position of reference point ${\bf A}'_j $ is given by $ {\bf A}'_j = (X_j^{(A)},0)^T $ while the coordinates of reference point $ {\bf B}'_j = {\bf R}(\zeta_j,t)$ may be obtained from a call to wall_pt->position(...). The nodal position $ {\bf r}_j $ may then be updated via

\[ {\bf r}_j = {\bf A}_j' + \omega_j \left( {\bf B}_j'-{\bf A}_j' \right) \]

How to use existing AlgebraicMeshes

To use the algebraic node-update capabilities of an existing AlgebraicMesh, all Nodes must be replaced by AlgebraicNodes to allow the storage of the node-specific node-update parameters. Recall that within oomph-lib Nodes are usually created by the elements, using the function FiniteElement::construct_node(...) whose argument specifies the local node number of the newly created Node within the element that creates it. (The specification of the local node number is required to allow the FiniteElement::construct_node(...) function to create a Node with the appropriate number of values and history values. For instance, in 2D Taylor-Hood Navier-Stokes elements, the elements' vertex nodes have to store three values, representing the two velocity components and the pressure, whereas all other nodes only require storage for the two velocity components.)

To ensure that the FiniteElement::construct_node(...) function creates AlgebraicNodes rather than "ordinary" Nodes, we provide the templated wrapper class

template<ELEMENT>
class AlgebraicElement<ELEMENT> : public ELEMENT

which overloads the FiniteElement::construct_node(...) function so that it creates AlgebraicNodes instead. In most other respects, the "wrapped" element behaves exactly as the underlying ELEMENT itself. To use an existing AlgebraicMesh with a certain element type, QTaylorHoodElement<2>, say, we simply "upgrade" the element to an AlgebraicElement by specifying the element type as AlgebraicElement<QTaylorHoodElement<2> >.

The changes to an existing driver code that performs the node update by the default Domain/MacroElement methodology are therefore completely trivial. You may wish to compare the driver code collapsible_channel.cc, discussed in an earlier example, to the driver code collapsible_channel_algebraic.cc in which the fluid domain is discretised by the MyAlgebraicCollapsibleChannelMesh, discussed below.

How to create a new AlgebraicMesh – a basic example

To illustrate how to create a new AlgebraicMesh, we will now discuss the implementation of the MyAlgebraicCollapsibleChannelMesh – an AlgebraicMesh - version of the CollapsibleChannelMesh, used in the earlier example.

The class definition

We construct the mesh by multiple inheritance from the AlgebraicMesh base class, and the already-existing CollapsibleChannelMesh. The constructor first calls the constructor of the underlying CollapsibleChannelMesh (thus "recycling" the basic mesh generation process, i.e. the generation of nodes and elements etc.) and then adds the algebraic node-update information by calling the function setup_algebraic_node_update().

//===========start_algebraic_mesh==================================
/// Collapsible channel mesh with algebraic node update
//=================================================================
template<class ELEMENT>
class MyAlgebraicCollapsibleChannelMesh :
public AlgebraicMesh,
public virtual CollapsibleChannelMesh<ELEMENT>
{
public:
/// Constructor: Pass number of elements in upstream/collapsible/
/// downstream segment and across the channel; lengths of upstream/
/// collapsible/downstream segments and width of channel, pointer to
/// GeomObject that defines the collapsible segment, and pointer to
/// TimeStepper (defaults to the default timestepper, Steady).
MyAlgebraicCollapsibleChannelMesh(const unsigned& nup,
const unsigned& ncollapsible,
const unsigned& ndown,
const unsigned& ny,
const double& lup,
const double& lcollapsible,
const double& ldown,
const double& ly,
GeomObject* wall_pt,
TimeStepper* time_stepper_pt=
&Mesh::Default_TimeStepper) :
CollapsibleChannelMesh<ELEMENT>(nup, ncollapsible, ndown, ny,
lup, lcollapsible, ldown, ly,
wall_pt,
time_stepper_pt)
{
// Setup algebraic node update operations
setup_algebraic_node_update();
}

We declare the interface for the pure virtual function algebraic_node_update(...), to be discussed below, and implement a second pure virtual function, AlgebraicMesh::update_node_update(), that may be used to update reference values following a mesh adaptation. Since the current mesh is not refineable, we leave this function empty and refer to another example for a more detailed discussion of its role.

/// Update nodal position at time level t (t=0: present;
/// t>0: previous)
void algebraic_node_update(const unsigned& t, AlgebraicNode*& node_pt);
/// Update the geometric references that are used
/// to update node after mesh adaptation.
/// Empty -- no update of node update required
void update_node_update(AlgebraicNode*& node_pt) {}

The protected member function setup_algebraic_node_update() will be discussed below.

protected:
/// Function to setup the algebraic node update
void setup_algebraic_node_update();
/// Dummy function pointer
CollapsibleChannelDomain::BLSquashFctPt Dummy_fct_pt;
};

Setting up the algebraic node update

When the function setup_algebraic_node_update() is called, the constructor of the underlying CollapsibleChannelMesh will already have created the mesh's elements and nodes, and the nodes will be located at their initial positions in the undeformed domain.

To set up the algebraic node-update data, we start by extracting the lengths of the upstream rigid section, $ L_{up} $, and the length of the collapsible segment, $ L_{collapsible} $, from the CollapsibleChannelDomain:

//============start_setup_algebraic_node_update====================
/// Setup algebraic mesh update -- assumes that mesh has
/// initially been set up with the wall in its undeformed position.
//=================================================================
template<class ELEMENT>
void MyAlgebraicCollapsibleChannelMesh<ELEMENT>::setup_algebraic_node_update()
{
// Extract some reference lengths from the CollapsibleChannelDomain.
double l_up=this->domain_pt()->l_up();
double l_collapsible=this->domain_pt()->l_collapsible();

Next, we loop over all AlgebraicNodes in the mesh and determine their current positions:

// Loop over all nodes in mesh
unsigned nnod=this->nnode();
for (unsigned j=0;j<nnod;j++)
{
// Get pointer to node
AlgebraicNode* nod_pt=node_pt(j);
// Get coordinates
double x=nod_pt->x(0);
double y=nod_pt->x(1);

If the j -th node is located in the "collapsible" section of the mesh we determine its reference coordinate, $ \zeta_j $, on the wall and determine the coordinates of its reference point $ {\bf B}_j $ from the GeomObject that represents the moving wall.

// Check if the node is in the collapsible part:
if ( (x>=l_up) && (x<=(l_up+l_collapsible)) )
{
// Get zeta coordinate on the undeformed wall
Vector<double> zeta(1);
zeta[0]=x-l_up;
// Get position vector to wall:
Vector<double> r_wall(2);
this->Wall_pt->position(zeta,r_wall);

Just to be on the safe side, we check that the wall is actually in its undeformed configuration, as assumed.

// Sanity check: Confirm that the wall is in its undeformed position
#ifdef PARANOID
if ((std::abs(r_wall[0]-x)>1.0e-15)&&(std::abs(r_wall[1]-y)>1.0e-15))
{
std::ostringstream error_stream;
error_stream
<< "Wall must be in its undeformed position when\n"
<< "algebraic node update information is set up!\n "
<< "x-discrepancy: " << std::abs(r_wall[0]-x) << std::endl
<< "y-discrepancy: " << std::abs(r_wall[1]-y) << std::endl;
throw OomphLibError(
error_stream.str(),
OOMPH_CURRENT_FUNCTION,
OOMPH_EXCEPTION_LOCATION);
}
#endif

Next, we package the data required for the node-update operations (the pointers to GeomObject(s) and the reference values) into vectors. In the present example, the node-update operation only involves a single GeomObject:

// Only a single geometric object is involved in the node update operation
Vector<GeomObject*> geom_object_pt(1);
// The wall geometric object
geom_object_pt[0]=this->Wall_pt;

We have three reference values: The $ x_1 $ - coordinate of point $ {\bf A}_j $,

// The update function requires three parameters:
Vector<double> ref_value(3);
// First reference value: Original x-position on the lower wall
ref_value[0]=r_wall[0];

as well as the fractional height, $ \omega_j $,

// Second reference value: Fractional position along
// straight line from the bottom (at the original x-position)
// to the point on the wall
ref_value[1]=y/r_wall[1];

and the reference coordinate, $ \zeta_j $, along the wall:

// Third reference value: Zeta coordinate on wall
ref_value[2]=zeta[0];

The vectors of reference values and geometric objects are then passed to the node, together with the pointer to the mesh (this) that implements the node-update function.

// Setup algebraic update for node: Pass update information
// to AlgebraicNode:
nod_pt->add_node_update_info(
this, // mesh
geom_object_pt, // vector of geom objects
ref_value); // vector of ref. values
}
}
} //end of setup_algebraic_node_update

The node-update function

The function algebraic_node_update(...) reverses the setup process: It extracts the node-update data from the AlgebraicNode and updates its position at the t -th previous time-level:

//=============start_of_algebraic_node_update======================
/// Perform algebraic mesh update at time level t (t=0: present;
/// t>0: previous)
//=================================================================
template<class ELEMENT>
void MyAlgebraicCollapsibleChannelMesh<ELEMENT>::algebraic_node_update(
const unsigned& t, AlgebraicNode*& node_pt)
{

We start by extracting the vectors of reference values and GeomObjects involved in this node's node-update, using the functions AlgebraicNode::vector_ref_value() which returns a Vector of reference values, and the function
AlgebraicNode::vector_geom_object_pt() which returns a Vector of pointers to GeomObjects.

// Extract reference values for update by copy construction
Vector<double> ref_value(node_pt->vector_ref_value());
// Extract geometric objects for update by copy construction
Vector<GeomObject*> geom_object_pt(node_pt->vector_geom_object_pt());

Next, we translate these into local variables,

// First reference value: Original x-position
double x_bottom=ref_value[0];
// Second reference value: Fractional position along
// straight line from the bottom (at the original x-position)
// to the point on the wall
double fract=ref_value[1];
// Third reference value: Zeta coordinate on wall
Vector<double> zeta(1);
zeta[0]=ref_value[2];
// Pointer to wall geom object
GeomObject* wall_pt=geom_object_pt[0];

and obtain the current wall position from the wall GeomObject.

// Get position vector to wall at previous timestep t
Vector<double> r_wall(2);
wall_pt->position(t,zeta,r_wall);

Finally, we update the nodal position:

// Assign new nodal coordinates
node_pt->x(t,0)=x_bottom+fract*(r_wall[0]-x_bottom);
node_pt->x(t,1)= fract* r_wall[1];
}

Done!

Comments and Exercises

Comments

  • Element-by-element and global node updates:

    As explained above, the re-implementation of the (empty) Node::node_update() function by AlgebraicNode::node_update() allows each node to "update its own position". The AlgebraicMesh and AlgebraicElement classes provide their own re-implementation of the node_update() functions in the Mesh and FiniteElement classes, and perform the node-updates by executing the AlgebraicNode::node_update() function of their constituent nodes.

  • Default node-update function:

    We stress that, in the above example, it was only necessary to set up the node-update data for the nodes in the central "collapsible" part of the mesh as they are the only modes whose position is affected by the motion of the curvilinear boundary. This is possible because the AlgebraicNode constructor provides default assignments for the node-update data. In particular, the pointer to the Mesh that performs the node update is initialised by a pointer to the (static instantiation of a) DummyMesh whose AlgebraicMesh::algebraic_node_update(...) and AlgebraicMesh::update_node_update(...) functions are empty. This ensures that nodes for which these default assignments are not overwritten stay at their original position when the node udate is performed. This implementation provides a sensible default behaviour for the node update.

  • Multiple node-update functions:

    In the simple example considered here, a single node-update function was sufficient to update the positions of all moving nodes in the mesh. In more complicated meshes, it may be be necessary to provide different node-update functions for nodes that are located in different parts of the mesh. To facilitate the implementation of such cases, it is possible to specify an identifier for the node-update function when calling the AlgebraicNode::add_node_update_info(...) function, using its alternative interface
    void AlgebraicNode::add_node_update_info(
    const int& id, // ID of the node-update fct
    AlgebraicMesh* mesh_pt, // pointer to mesh
    const Vector<GeomObject*>& geom_object_pt, // vector of geom objects
    const Vector<double>& ref_value); // vector of ref. values
    When implementing the AlgebraicMesh::algebraic_node_update(...) function for a mesh that contains multiple node-update functions, the ID of the node-update function associated with a particular node can be obtained from AlgebraicNode::node_update_fct_id(), allowing the node-update function to take the appropriate action. (As an example, consider the implementation of the algebraic node-update function for the RefineableAlgebraicFishMesh in which different node-update functions are used to update the position of nodes in the fish's "body" and in its "tail".) If the AlgebraicNode::add_node_update_info(...) function is called without specifying an ID, a default ID of 0 is assigned.

  • Consistency between multiple node-update functions:

    If a mesh contains multiple node-update functions, it is likely that some nodes are located at the interface between regions that are updated by different node-update functions. As indicated by the "add_..." in the AlgebraicNode::add_node_update_info(...) function, AlgebraicNodes may be associated with multiple node-update functions, though the different node-update functions associated with a node must, of course, give the same result. This may be verified by calling the AlgebraicNode::self_test() function for all nodes in an AlgebraicMesh.

    Note: In refineable AlgebraicMeshes (discussed in more detail below), AlgebraicNodes must be associated with all possible node-update functions to ensure that the reference values for newly created nodes are determined correctly during the adaptive mesh refinement.

  • Adaptivity:

    Refineable AlgebraicMeshes may be created by multiple inheritance from a suitable RefineableMesh base class (e.g. the RefineableQuadMesh class), and setting up the required tree representation of the coarse initial mesh, exactly as for "ordinary" meshes (see the tutorial "How to create simple refineable meshes" for details). As an example, here is the class definition for a refineable version of the MyAlgebraicCollapsibleChannelMesh discussed above:

    //===========start_refineable_algebraic_collapsible_channel_mesh======
    /// Refineable version of the CollapsibleChannel mesh with
    /// algebraic node update.
    //====================================================================
    template<class ELEMENT>
    class MyRefineableAlgebraicCollapsibleChannelMesh :
    public RefineableQuadMesh<ELEMENT>,
    public virtual MyAlgebraicCollapsibleChannelMesh<ELEMENT>
    {
    public:
    /// Constructor: Pass number of elements in upstream/collapsible/
    /// downstream segment and across the channel; lengths of upstream/
    /// collapsible/downstream segments and width of channel, pointer to
    /// GeomObject that defines the collapsible segment, function pointer
    /// to "boundary layer squash function", and pointer to
    /// TimeStepper (defaults to the default timestepper, Steady).
    MyRefineableAlgebraicCollapsibleChannelMesh(const unsigned& nup,
    const unsigned& ncollapsible,
    const unsigned& ndown,
    const unsigned& ny,
    const double& lup,
    const double& lcollapsible,
    const double& ldown,
    const double& ly,
    GeomObject* wall_pt,
    TimeStepper* time_stepper_pt=
    &Mesh::Default_TimeStepper) :
    CollapsibleChannelMesh<ELEMENT>(nup, ncollapsible, ndown, ny,
    lup, lcollapsible, ldown, ly,
    wall_pt,
    time_stepper_pt),
    MyAlgebraicCollapsibleChannelMesh<ELEMENT>(nup, ncollapsible, ndown, ny,
    lup, lcollapsible, ldown, ly,
    wall_pt,
    time_stepper_pt)
    {
    // Build quadtree forest
    this->setup_quadtree_forest();
    }
    };

    Note that none of the functions defined in the non-refineable version of this mesh have to be re-implemented. This raises the question of how the node-update data for any newly created nodes are determined when the mesh is refined. By default, the reference values for any newly created AlgebraicNodes are determined by interpolation from the node's "father element". Furthermore, it is assumed
    that the same GeomObjects are involved in the node-update function for the newly created node.
    This default behaviour is appropriate for the mesh considered here. In other cases, (e.g. in the corresponding fluid-structure interaction problem), some or all of the node-update data may have to be recomputed when the mesh is adapted. Such updates may be performed by the AlgebraicMesh::update_node_update(...) function which is executed automatically whenever a refineable AlgebraicMesh is adapted.

  • Node updates for hanging nodes:

    Recall that refineable meshes may contain hanging nodes whose position is constrained by its "master nodes". When the AlgebraicNode::node_update(...) function is called for a hanging node, it first updates the position of its master nodes (using their own node-update functions) and then updates its own constrained position accordingly.

  • Automatic finite-differencing with respect to geometric Data:

    Algebraic node updates are particularly useful in fluid-structure interaction problems since they allow the development of "sparse" node update procedures in which each (solid mechanics) degree of freedom only affects the position of a small number of nodes in the fluid mesh. We will discuss fluid-structure interaction problems in more detail elsewhere but stress already that one of the major complications in such problems (and, in fact, in any free-boundary problem) is the need to evaluate the so-called shape derivatives – the derivatives of the "bulk" (here the Navier-Stokes) equations with respect to the degrees of freedom (here the nodal positions in the wall mesh) that affect the position of the nodes in the "bulk" mesh.

    The algebraic node update procedures discussed above are sufficiently general to handle such interactions. The shape/position of the GeomObjects that are involved in an AlgebraicNode's node update, may depend on unknowns in the overall problem. Such unknowns constitute a GeomObject's geometric Data which may be obtained from its member function GeomObject::geom_data_pt(...). AlgebraicElements use finite differencing to include the shape derivatives (i.e. the derivatives of the residuals of the underlying (wrapped) element with respect to the geometric Data involved in the element's node update) into the element's Jacobian matrix.

  • Additional sanity checks and other generalisations:

    The MyAlgebraicCollapsibleChannelMesh and its refineable equivalent are slightly simplified versions of the meshes in oomph-lib's src/meshes directory. These meshes contain a number of additional sanity checks that we omitted here for the sake of brevity. Furthermore, these meshes can be used with GeomObjects that comprise "sub-"GeomObjects, a feature that is essential in problems with proper fluid-structure interaction. We will discuss this in another example.

Exercises

  1. If you inspect the
    source code for the MyAlgebraicCollapsibleChannelMesh, you will notice that the mesh has an additional constructor that allows the specification of the "boundary layer squash function" first introduced in the original CollapsibleChannelMesh. Explain why in the AlgebraicMesh version of this mesh, the function pointer to the "boundary layer squash function" can only be specified via the constructor – the access function is deliberately broken.

Source files for this tutorial

PDF file

A pdf version of this document is available.