In this example we consider our first moving-boundary Navier-Stokes problem: The flow of a viscous fluid contained in an elliptical ring whose walls perform periodic oscillations.

oomph-lib's Navier-Stokes elements are based on the Arbitrary Lagrangian Eulerian (ALE) form of the Navier-Stokes equations and can therefore be used in moving domain problems. In this example we illustrate their use in Domain - based meshes (first discussed in the example demonstrating the solution of the unsteady heat equation in a moving domain) in which MacroElements are used to update the nodal positions in response to changes in the domain boundary. In subsequent examples, we will discuss alternative, sparse mesh update techniques that are useful in problems with free boundaries and in fluid-structure interaction problems.

Finite-Reynolds-number-flow driven by an oscillating ellipse

We consider the unsteady 2D flow of a Newtonian fluid that is contained in an oscillating elliptical ring whose wall shape is parametrised by the Lagrangian coordinate $\xi$ as

${\bf R}_w(\xi) = \left( \begin{array}{l} a(t) \cos(\xi) \\ a^{-1}(t) \sin(\xi) \end{array} \right)$

where

$a(t) = A + \widehat{A} \cos\left(\frac{2\pi t}{T}\right).$

represents the average half-axis of the elliptical ring in the -direction, and $\widehat{A}$ is the amplitude of its periodic variation. The ring has constant cross-sectional area – consistent with the incompressibility of the fluid whose motion is governed by the ALE form of the Navier-Stokes equations,

$Re\left(St\frac{\partial u_i}{\partial t} + \left(u_j-u_j^M\right)\frac{\partial u_i}{\partial x_j}\right) = - \frac{\partial p}{\partial x_i} + \frac{\partial }{\partial x_j} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right), \ \ \ \ \ \ \ \ \ \ (1)$

and the continuity equation

$\frac{\partial u_i}{\partial x_i} = 0,$

where is the mesh velocity. We exploit the symmetry of the problem and solve the equations in the quarter domain

$D = \left\{(x_1,x_2) \, \bigg| \, x_1\geq0, \, x_2\geq0,\, \left(\frac{x_1}{a(t)}\right)^2 + \big(x_2 \, a(t)\big)^2 \leq 1\right\},$

shown in this sketch (for 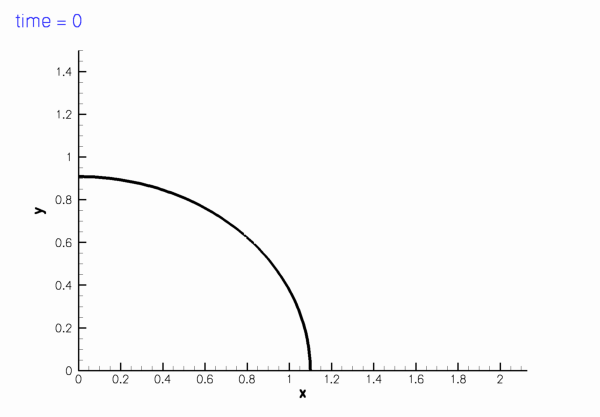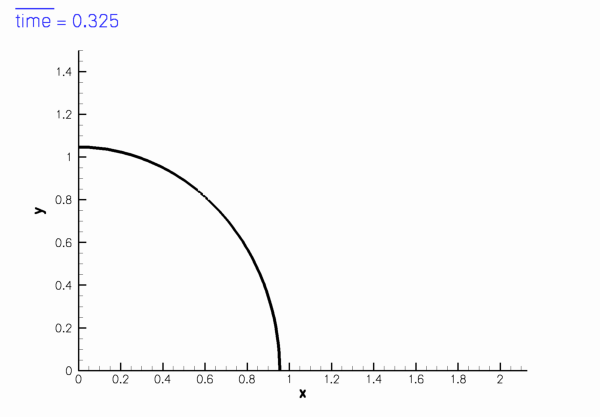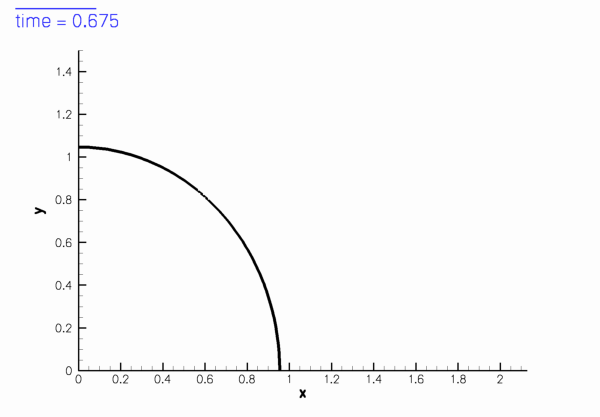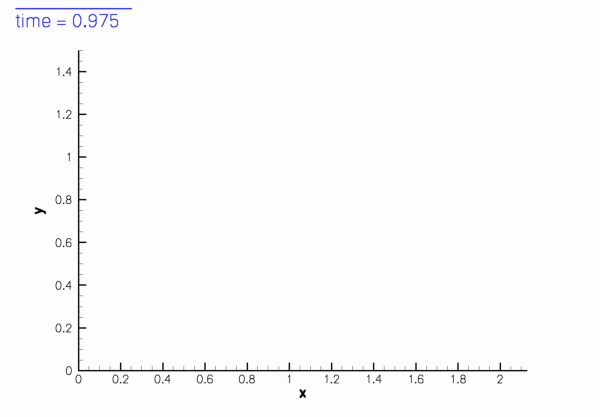$A=1, \ \widehat{A}=1$ and ),

Sketch of the computational domain.

The fluid is subject to no-slip boundary conditions on the curved wall,

$\left. {\bf u} \right|_{\partial D_{ellipse}} = \frac{\partial {\bf R}_w(\xi, t)}{\partial t}$

and symmetry conditions on the symmetry boundaries,

$\left.u_1\right|_{x_2=0}=0, \qquad \left.u_2\right|_{x_1=0}=0.$

The initial conditions for the velocity are given by

${\bf u}(x_1,x_2,t=0) = {\bf u}_{IC}(x_1,x_2),$

where ${\bf u}_{IC}(x_1,x_2)$ is a given, divergence-free velocity field that satisfies the velocity boundary conditions at . No initial conditions are required for the pressure.

An exact solution

It is easy to show (by inspection) that the unsteady stagnation point flow

$u_1(x_1,x_2,t) = \frac{1}{a}\frac{da}{dt}\, x_1 = -\frac{2\pi\widehat{A}\sin\left(\frac{2\pi t}{T}\right)} {T\left(A+\widehat{A}\cos\left(\frac{2\pi t}{T}\right)\right)} \, x_1 \mbox{\ \ \ \ and \ \ \ \ \ } u_2(x_1,x_2,t) = -\frac{1}{a}\frac{da}{dt} \, x_2 = -\frac{2\pi\widehat{A}\sin\left(\frac{2\pi t}{T}\right)} {T\left(A+\widehat{A}\cos\left(\frac{2\pi t}{T}\right)\right)} \, x_2,$

is an exact solution of the above problem as it satisfies the Navier-Stokes equations and the velocity boundary conditions. The pressure is given by

$p = \frac{2\pi\widehat{A}\, Re\, \left(x_1^2\, St\, \cos\left(\frac{2\pi t}{T}\right)A + x_1^2\, St\, \widehat{A} - x_1^2\widehat{A} + x_1^2\widehat{A}\cos^2\left(\frac{2\pi t}{T}\right) - x_2^2\, St\, \cos\left(\frac{2\pi t}{T}\right) - x_2^2\, St\, \widehat{A} - x_2^2\widehat{A} + x_2^2\widehat{A}\cos^2\left(\frac{2\pi t}{T}\right)\right)} {T^2\left(A^2 + 2A\widehat{A}\cos\left(\frac{2\pi t}{T}\right) + \widehat{A}^2\cos^2\left(\frac{2\pi t}{T}\right)\right)}.$

Results

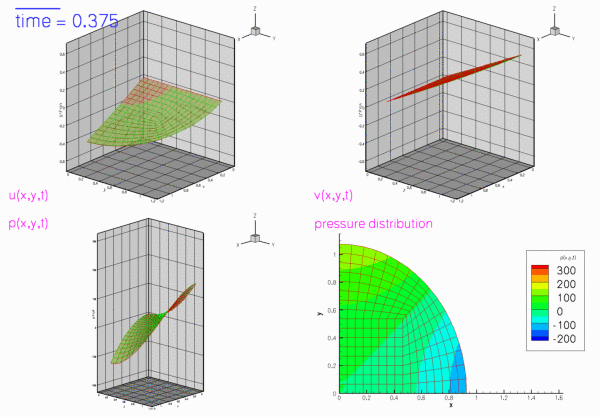
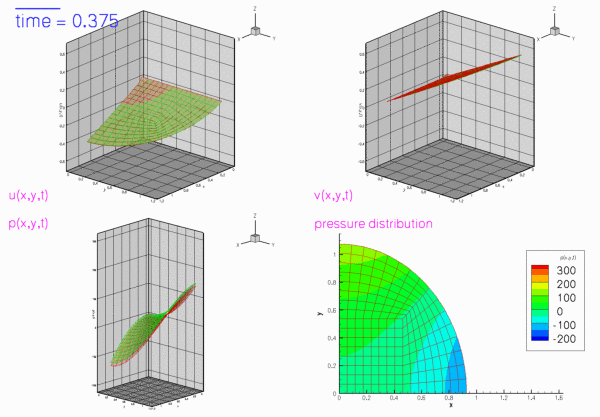
The two figures below show two snapshots of the solution for $Re=Re \ St=100$ , extracted from an animations of the results computed with Taylor-Hood and Crouzeix-Raviart elements. In both cases, the exact solution was used as the initial condition for the velocities. The figures show "carpet plots" of the two velocity components and the pressure, respectively, and a contour plot of the pressure, superimposed on the moving mesh. The carpet plot of the velocities clearly shows that the flow is of stagnation-point type as the horizontal velocity, , is a linear function of while the vertical velocity, , is a linear function of .

Plot of the velocity and pressure fields computed with 2D Crouzeix-Raviart elements, with Re=100 and St=1.

Plot of the velocity and pressure fields computed with 2D Taylor-Hood elements, with Re=100 and St=1.

The moving wall

As usual, we represent the moving wall as a GeomObject and define its shape by implementing the pure virtual function GeomObject::position(...). The arguments to the constructor specify the mean half-axis of the ellipse, , the amplitude of its variations, $\widehat{A}$ , and the period of the oscillation, . We also pass the pointer to a Time object to the constructor and store it in a private data member, to allow the position(...) functions to access the current value of the continuous time.

//============start_of_MyEllipse===========================================
/// Oscillating ellipse
/// \f[ x = (A + \widehat{A} \cos(2\pi t/T)) \cos(\xi)  \f]
/// \f[ y = \frac{\sin(\xi)}{A + \widehat{A} \cos(2\pi t/T)}   \f]
/// Note that cross-sectional area is conserved.
//=========================================================================
class MyEllipse : public GeomObject
{
 
public:
 
 /// Constructor:  Pass initial x-half axis, amplitude of x-variation, 
 /// period of oscillation and pointer to time object.
 MyEllipse(const double& a, const double& a_hat,
           const double& period, Time* time_pt) : 
  GeomObject(1,2), A(a), A_hat(a_hat), T(period), Time_pt(time_pt) {}
 
 /// Destructor: Empty
 virtual ~MyEllipse() {}
 
 /// Current position vector to material point at 
 /// Lagrangian coordinate xi 
 void position(const Vector<double>& xi, Vector<double>& r) const
  {
   // Get current time:
   double time=Time_pt->time();
 
   // Position vector
   double axis=A+A_hat*cos(2.0*MathematicalConstants::Pi*time/T);
   r[0] = axis*cos(xi[0]);
   r[1] = (1.0/axis)*sin(xi[0]);
  } 
 
 /// Parametrised position on object: r(xi). Evaluated at
 /// previous time level. t=0: current time; t>0: previous
 /// time level.
 void position(const unsigned& t, const Vector<double>& xi,
               Vector<double>& r) const
  {
   // Get current time:
   double time=Time_pt->time(t);
   
   // Position vector
   double axis=A+A_hat*cos(2.0*MathematicalConstants::Pi*time/T);
   r[0] = axis*cos(xi[0]);
   r[1] = (1.0/axis)*sin(xi[0]);
  } 
 
private:
 
 /// x-half axis
 double A;
 
 /// Amplitude of variation in x-half axis
 double A_hat;
 
 /// Period of oscillation
 double T;
 
 /// Pointer to time object
 Time* Time_pt;
 
}; // end of MyEllipse

The global parameters

As in most previous examples, we use a namespace to define and initialise global problem parameters such as the Reynolds and Strouhal numbers:

//===start_of_namespace=================================================
/// Namepspace for global parameters
//======================================================================
namespace Global_Physical_Variables
{
 
 /// Reynolds number
 double Re=100.0;
 
 /// Womersley = Reynolds times Strouhal
 double ReSt=100.0;

We also define and initialise the parameters that specify the motion of the domain boundary and specify the exact solution.

 
 /// x-Half axis length
 double A=1.0;
 
 /// x-Half axis amplitude
 double A_hat=0.1;
 
 /// Period of oscillations
 double T=1.0;
 
 /// Exact solution of the problem as a vector containing u,v,p
 void get_exact_u(const double& t, const Vector<double>& x, Vector<double>& u)
 {
  using namespace MathematicalConstants;
 
  // Strouhal number
  double St = ReSt/Re;
 
  // Half axis
  double a=A+A_hat*cos(2.0*Pi*t/T);
  double adot=-2.0*A_hat*Pi*sin(2.0*Pi*t/T)/T; 
  u.resize(3);
 
  // Velocity solution
  u[0]=adot*x[0]/a;
  u[1]=-adot*x[1]/a;
 
  // Pressure solution
  u[2]=(2.0*A_hat*Pi*Pi*Re*(x[0]*x[0]*St*cos(2.0*Pi*t/T)*A + 
                            x[0]*x[0]*St*A_hat - x[0]*x[0]*A_hat +
                            x[0]*x[0]*A_hat*cos(2.0*Pi*t/T)*cos(2.0*Pi*t/T) -
                            x[1]*x[1]*St*cos(2.0*Pi*t/T)*A - 
                            x[1]*x[1]*St*A_hat - x[1]*x[1]*A_hat +
                            x[1]*x[1]*A_hat*cos(2.0*Pi*t/T)*cos(2.0*Pi*t/T) ))
   /(T*T*(A*A + 2.0*A*A_hat*cos(2.0*Pi*t/T) + 
          A_hat*A_hat*cos(2.0*Pi*t/T)*cos(2.0*Pi*t/T) ));
 }
 
 
} // end of namespace

The driver code

As in most previous unsteady demo codes, we allow the code to be run in a validation mode (in which we use a coarser mesh and execute fewer timesteps). This mode is selected by specifying an (arbitrary) command line argument that we store in the namespace CommandLineArgs.

//======start_of_main=================================================
/// Driver code for unsteady Navier-Stokes flow, driven by
/// oscillating ellipse. If the code is executed with command line
/// arguments, a validation run is performed. 
//====================================================================
int main(int argc, char* argv[])
{
 
 // Store command line arguments
 CommandLineArgs::setup(argc,argv);

We create a DocInfo object to specify the output directory, build the problem with adaptive Crouzeix-Raviart elements and the BDF<2> timestepper and perform the unsteady simulation.

 
 
 // Solve with Crouzeix-Raviart elements
 {
  // Create DocInfo object with suitable directory name for output
  DocInfo doc_info;
  doc_info.set_directory("RESLT_CR");
  
  //Set up problem
  OscEllipseProblem<RefineableQCrouzeixRaviartElement<2>,BDF<2> > problem;
  
  // Run the unsteady simulation
  problem.unsteady_run(doc_info);
 }

Then we repeat this process for adaptive Taylor-Hood elements.

 
 // Solve with Taylor-Hood elements
 {
  // Create DocInfo object with suitable directory name for output
  DocInfo doc_info;
  doc_info.set_directory("RESLT_TH");
 
  //Set up problem
  OscEllipseProblem<RefineableQTaylorHoodElement<2>,BDF<2> > problem;
  
  // Run the unsteady simulation
  problem.unsteady_run(doc_info);
 }
 
 
}; // end of main

The problem class

Most of the problem class is a straightforward combination of the problem classes employed in the simulation of the adaptive driven cavity and Rayleigh channel problems, in that the problem combines unsteadiness with spatial adaptivity (though in the present problem the adaptivity is only used to uniformly refine the very coarse base mesh; we refer to another example for the use of full spatial adaptivity in a moving-domain Navier-Stokes problem).

//=====start_of_problem_class=========================================
/// Navier-Stokes problem in an oscillating ellipse domain.
//====================================================================
template<class ELEMENT, class TIMESTEPPER>
class OscEllipseProblem : public Problem
{
 
public:
 
 /// Constructor
 OscEllipseProblem();
 
 /// Destructor (empty)
 ~OscEllipseProblem() {}
 
 /// Update the problem specs after solve (empty)
 void actions_after_newton_solve(){}
 
 /// Update problem specs before solve (empty)
 void actions_before_newton_solve() {} 
 
 /// Actions before adapt (empty)
 void actions_before_adapt(){}
 
 /// Actions after adaptation, pin relevant pressures
 void actions_after_adapt()
  {
   // Unpin all pressure dofs
   RefineableNavierStokesEquations<2>::
    unpin_all_pressure_dofs(mesh_pt()->element_pt());
 
   // Pin redundant pressure dofs
   RefineableNavierStokesEquations<2>::
    pin_redundant_nodal_pressures(mesh_pt()->element_pt());
   
   // Now set the first pressure dof in the first element to 0.0
   fix_pressure(0,0,0.0);
 
  } // end of actions_after_adapt

The key new feature in the current problem is the presence of the moving domain which requires updates of

all nodal positions
the prescribed velocities on the moving wall via the no-slip condition.

before every timestep. Since the nodal positions of the QuarterCircleSectorMesh are determined via its MacroElement / Domain representation (which updates the nodal position in response to changes in the geometry of the GeomObjects that define its boundaries), the former task may be accomplished by executing the Mesh::node_update() function; the update of the no-slip condition may be performed by calling the function FSI_functions::apply_no_slip_on_moving_wall(Node* node_pt), a helper function, defined in the namespace FSI_functions, which updates the velocity components according to the no-slip boundary condition

${\bf u}_{Node} = \frac{\partial {\bf x}_{Node}}{\partial t}$

where the time-derivative of the nodal positions is evaluated by the Node's positional timestepper. [Note: The function FSI_functions::apply_no_slip_on_moving_wall(...) assumes that the velocity components are stored in the Node's first 2 [3] values. This is consistent with the storage of the velocity component in all existing Navier-Stokes elements. If you develop your own Navier-Stokes elements and use a different storage scheme you use this function at your own risk.]

Here is the implementation of these tasks:

 
 
 /// Update the problem specs before next timestep
 void actions_before_implicit_timestep()
  {
   // Update the domain shape
   mesh_pt()->node_update();
 
   // Ring boundary: No slip; this implies that the velocity needs
   // to be updated in response to wall motion
   unsigned ibound=1;
   unsigned num_nod=mesh_pt()->nboundary_node(ibound);
   for (unsigned inod=0;inod<num_nod;inod++)
    {
     // Which node are we dealing with?
     Node* node_pt=mesh_pt()->boundary_node_pt(ibound,inod);
     
     // Apply no slip
     FSI_functions::apply_no_slip_on_moving_wall(node_pt);
    }
  } 
 
 /// Update the problem specs after timestep (empty)
 void actions_after_implicit_timestep(){}

The remaining functions are similar to those used in our previous Navier-Stokes examples and require no further explanation.

 
 /// Doc the solution
 void doc_solution(DocInfo& doc_info);
 
 /// Timestepping loop
 void unsteady_run(DocInfo& doc_info);
 
 /// Set initial condition
 void set_initial_condition();
 
private:
 
 /// Fix pressure in element e at pressure dof pdof and set to pvalue
 void fix_pressure(const unsigned &e, const unsigned &pdof, 
                   const double &pvalue)
  {
   //Cast to proper element and fix pressure
   dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(e))->
    fix_pressure(pdof,pvalue);
  } // end_of_fix_pressure
 
 /// Pointer to GeomObject that specifies the domain bondary
 GeomObject* Wall_pt;
 
}; // end of problem_class

The problem constructor

We start by creating a timestepper of the type specified by the Problem's template parameter and add (a pointer to) it to the Problem's collection of Timesteppers. Recall that this function also creates the Problem's Time object.

 
 
 
//========start_of_constructor============================================
/// Constructor for Navier-Stokes problem on an oscillating ellipse domain.
//========================================================================
template<class ELEMENT, class TIMESTEPPER>
OscEllipseProblem<ELEMENT,TIMESTEPPER>::OscEllipseProblem()
{ 
 
 //Create the timestepper and add it to the problem
 add_time_stepper_pt(new TIMESTEPPER);

Next we create the GeomObject that defines the curvilinear domain boundary and pass it to the Mesh constructor. (Since we will only use adaptivity to refine the mesh uniformly, it is not necessary to define an error estimator.)

 
 // Setup mesh
 //-----------
 
 // Build geometric object that forms the curvilinear domain boundary:
 // an oscillating ellipse
 
 // Half axes
 double a=Global_Physical_Variables::A;
 
 // Variations of half axes
 double a_hat=Global_Physical_Variables::A_hat;
 
 // Period of the oscillation
 double period=Global_Physical_Variables::T;
 
 // Create GeomObject that specifies the domain bondary
 Wall_pt=new MyEllipse(a,a_hat,period,Problem::time_pt()); 
 
 
 // Start and end coordinates of curvilinear domain boundary on ellipse
 double xi_lo=0.0;
 double xi_hi=MathematicalConstants::Pi/2.0;
 
 // Now create the mesh. Separating line between the two 
 // elements next to the curvilinear boundary is located half-way
 // along the boundary.
 double fract_mid=0.5;
 Problem::mesh_pt() = new RefineableQuarterCircleSectorMesh<ELEMENT>(
  Wall_pt,xi_lo,fract_mid,xi_hi,time_stepper_pt());
 
 // Set error estimator NOT NEEDED IN CURRENT PROBLEM SINCE 
 // WE'RE ONLY REFINING THE MESH UNIFORMLY
 //Z2ErrorEstimator* error_estimator_pt=new Z2ErrorEstimator;
 //mesh_pt()->spatial_error_estimator_pt()=error_estimator_pt;

Both velocity components on the curvilinear mesh boundary are determined by the no-slip condition and must therefore be pinned,

 
 
 // Fluid boundary conditions
 //--------------------------
 // Ring boundary: No slip; this also implies that the velocity needs
 // to be updated in response to wall motion
 unsigned ibound=1;
 {
  unsigned num_nod= mesh_pt()->nboundary_node(ibound);
  for (unsigned inod=0;inod<num_nod;inod++)
   {
     
    // Pin both velocities
    for (unsigned i=0;i<2;i++)
     {
      mesh_pt()->boundary_node_pt(ibound,inod)->pin(i);
     }
   }
 } // end boundary 1

whereas on the symmetry boundaries only one of the two velocity components is set to zero:

 // Bottom boundary: 
 ibound=0;
 {
  unsigned num_nod= mesh_pt()->nboundary_node(ibound);
  for (unsigned inod=0;inod<num_nod;inod++)
   {
    // Pin vertical velocity
    {
     mesh_pt()->boundary_node_pt(ibound,inod)->pin(1);
    }
   }
 } // end boundary 0
 
 // Left boundary:
 ibound=2;
 {
  unsigned num_nod= mesh_pt()->nboundary_node(ibound);
  for (unsigned inod=0;inod<num_nod;inod++)
   {
    // Pin horizontal velocity
    {
     mesh_pt()->boundary_node_pt(ibound,inod)->pin(0);
    }
   }
 } // end boundary 2

Finally, we pass the pointers to , $Re \ St$ and the global Time object (automatically created by the Problem when the timestepper was passed to it at the beginning of the constructor) to the elements, pin the redundant nodal pressure degrees of freedom (see the discussion of the adaptive driven-cavity problem for more details), pin one pressure degree of freedom, and set up the equation numbering scheme.

 
 
 // Complete the build of all elements so they are fully functional
 //----------------------------------------------------------------
 
 // Find number of elements in mesh
 unsigned n_element = mesh_pt()->nelement();
 
 // Loop over the elements to set up element-specific 
 // things that cannot be handled by constructor
 for(unsigned i=0;i<n_element;i++)
  {
   // Upcast from FiniteElement to the present element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(i));
 
   //Set the Reynolds number, etc
   el_pt->re_pt() = &Global_Physical_Variables::Re;
   el_pt->re_st_pt() = &Global_Physical_Variables::ReSt;
  }
 
 // Pin redundant pressure dofs
 RefineableNavierStokesEquations<2>::
  pin_redundant_nodal_pressures(mesh_pt()->element_pt());
 
 // Now set the first pressure dof in the first element to 0.0
 fix_pressure(0,0,0.0);
 
 // Do equation numbering
 cout << "Number of equations: " << assign_eqn_numbers() << std::endl; 
 
} // end of constructor

Assigning the initial conditions

This function assigns "history values" for the velocities and the nodal positions from the exact solution. It is implemented in exactly the same way as in the solution of the unsteady heat equation in a moving domain. Note that because the domain is moving, the nodal positions must be updated (according to the position of the domain boundary at the relevant previous timestep), before evaluating the exact solution at the nodal position.

//======================start_of_set_initial_condition====================
/// Set initial condition: Assign previous and current values
/// from exact solution.
//========================================================================
template<class ELEMENT,class TIMESTEPPER>
void OscEllipseProblem<ELEMENT,TIMESTEPPER>::set_initial_condition()
{ 
 // Backup time in global timestepper
 double backed_up_time=time_pt()->time();
   
 // Past history for velocities must be established for t=time0-deltat, ...
 // Then provide current values (at t=time0) which will also form
 // the initial guess for first solve at t=time0+deltat
 
 // Vector of exact solution value
 Vector<double> soln(3);
 Vector<double> x(2);
 
 //Find number of nodes in mesh
 unsigned num_nod = mesh_pt()->nnode();
 
 // Get continuous times at previous timesteps
 int nprev_steps=time_stepper_pt()->nprev_values();
 Vector<double> prev_time(nprev_steps+1);
 for (int itime=nprev_steps;itime>=0;itime--)
  {
   prev_time[itime]=time_pt()->time(unsigned(itime));
  }
 
 // Loop over current & previous timesteps (in outer loop because
 // the mesh also moves!)
 for (int itime=nprev_steps;itime>=0;itime--)
  {
   double time=prev_time[itime];
   
   // Set global time (because this is how the geometric object refers 
   // to continous time )
   time_pt()->time()=time;
   
   cout << "setting IC at time =" << time << std::endl;
   
   // Update the mesh for this value of the continuous time
   // (The wall object reads the continous time from the 
   // global time object)
   mesh_pt()->node_update(); 
   
   // Loop over the nodes to set initial guess everywhere
   for (unsigned jnod=0;jnod<num_nod;jnod++)
    {
     // Get nodal coordinates
     x[0]=mesh_pt()->node_pt(jnod)->x(0);
     x[1]=mesh_pt()->node_pt(jnod)->x(1);
     
     // Get exact solution (unsteady stagnation point flow)
     Global_Physical_Variables::get_exact_u(time,x,soln);
     
     // Assign solution
     mesh_pt()->node_pt(jnod)->set_value(itime,0,soln[0]);
     mesh_pt()->node_pt(jnod)->set_value(itime,1,soln[1]);
       
     // Loop over coordinate directions
     for (unsigned i=0;i<2;i++)
      {
       mesh_pt()->node_pt(jnod)->x(itime,i)=x[i];
      }
    } 
  } // end of loop over previous timesteps
 
 // Reset backed up time for global timestepper
 time_pt()->time()=backed_up_time;
 
} // end of set_initial_condition

Post processing

The function doc_solution(...) is similar to that in the unsteady heat examples and the previous Navier-Stokes examples. We add dummy zones and tecplot geometries to facilitate the post-processing of the results with tecplot.

//=======start_of_doc_solution============================================
/// Doc the solution
//========================================================================
template<class ELEMENT, class TIMESTEPPER>
void OscEllipseProblem<ELEMENT,TIMESTEPPER>::doc_solution(DocInfo& doc_info)
{ 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned npts;
 npts=5;
 
 // Output solution 
 //-----------------
 sprintf(filename,"%s/soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 mesh_pt()->output(some_file,npts);
 some_file << "TEXT X=2.5,Y=93.6,F=HELV,HU=POINT,C=BLUE,H=26,T=\"time = " 
           << time_pt()->time() << "\"";
 some_file << "GEOMETRY X=2.5,Y=98,T=LINE,C=BLUE,LT=0.4" << std::endl;
 some_file << "1" << std::endl;
 some_file << "2" << std::endl;
 some_file << " 0 0" << std::endl;
 some_file << time_pt()->time()*20.0 << " 0" << std::endl;
 
 // Write dummy zones that force tecplot to keep the axis limits constant
 // while the domain is moving.
 some_file << "ZONE I=2,J=2" << std::endl;
 some_file << "0.0 0.0 -0.65 -0.65 -200.0" << std::endl;
 some_file << "1.15 0.0 -0.65 -0.65 -200.0" << std::endl;
 some_file << "0.0 1.15 -0.65 -0.65 -200.0" << std::endl;
 some_file << "1.15 1.15 -0.65 -0.65 -200.0" << std::endl;
 some_file << "ZONE I=2,J=2" << std::endl;
 some_file << "0.0 0.0 0.65 0.65 300.0" << std::endl;
 some_file << "1.15 0.0 0.65 0.65 300.0" << std::endl;
 some_file << "0.0 1.15 0.65 0.65 300.0" << std::endl;
 some_file << "1.15 1.15 0.65 0.65 300.0" << std::endl;
 
 some_file.close();
 
 // Output exact solution 
 //----------------------
 sprintf(filename,"%s/exact_soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 mesh_pt()->output_fct(some_file,npts,time_pt()->time(),
                       Global_Physical_Variables::get_exact_u); 
 some_file.close();
 
 // Doc error
 //----------
 double error,norm;
 sprintf(filename,"%s/error%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 mesh_pt()->compute_error(some_file,
                          Global_Physical_Variables::get_exact_u,
                          time_pt()->time(),
                          error,norm); 
 some_file.close();
 
 
 // Doc solution and error
 //-----------------------
 cout << "error: " << error << std::endl; 
 cout << "norm : " << norm << std::endl << std::endl;
 
 
 // Plot wall posn
 //---------------
 sprintf(filename,"%s/Wall%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 
 unsigned nplot=100;
 for (unsigned iplot=0;iplot<nplot;iplot++)
  {
   Vector<double> xi_wall(1), r_wall(2);
   xi_wall[0]=0.5*MathematicalConstants::Pi*double(iplot)/double(nplot-1);
   Wall_pt->position(xi_wall,r_wall);
   some_file << r_wall[0] << " " << r_wall[1] << std::endl;
  }
 some_file.close();
 
 // Increment number of doc
 doc_info.number()++;
 
} // end of doc_solution

The timestepping loop

The timestepping loop is extremely straightforward: We choose a timestep and the overall length of the simulation, initialise the timestepper(s) by calling Problem::initialise_dt(...) and assign the initial condition.

//=======start_of_unsteady_run============================================
/// Unsteady run
//========================================================================
template<class ELEMENT, class TIMESTEPPER>
void OscEllipseProblem<ELEMENT,TIMESTEPPER>::unsteady_run(DocInfo& doc_info)
{
 
 // Specify duration of the simulation
 double t_max=3.0;
 
 // Initial timestep
 double dt=0.025;
 
 // Initialise timestep
 initialise_dt(dt);
 
 // Set initial conditions.
 set_initial_condition();

Next we set the number of timesteps for a normal run.

 
 // Alternative initial conditions: impulsive start; see exercise.
 //assign_initial_values_impulsive(); 
 
 // find number of steps
 unsigned nstep = unsigned(t_max/dt);

We over-write this number and perform a single uniform mesh refinement if the code is run in self-test mode (indicated by a non-zero number of command line arguments),

 
 // If validation: Reduce number of timesteps performed and 
 // use coarse-ish mesh
 if (CommandLineArgs::Argc>1)
  {
   nstep=2;
   refine_uniformly();
   cout << "validation run" << std::endl;
  }

otherwise we refine the mesh three times and output the initial conditions

 else
  {
   // Refine the mesh three times, to resolve the pressure distribution
   // (the velocities could be represented accurately on a much coarser mesh).
   refine_uniformly();
   refine_uniformly();
   refine_uniformly();
  }
 
 // Output solution initial 
 doc_solution(doc_info);

Finally we execute the proper timestepping loop and document the solution after every timestep

 
 // Timestepping loop
 for (unsigned istep=0;istep<nstep;istep++)
  {
   cout << "TIMESTEP " << istep << std::endl;
   cout << "Time is now " << time_pt()->time() << std::endl;
 
   // Take timestep 
   unsteady_newton_solve(dt);
     
   //Output solution
   doc_solution(doc_info);
  }
 
} // end of unsteady_run

Comments and Exercises

Compare the results of the numerical simulation in which 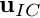${\bf u}_{IC}$ is given by the exact solution (an unsteady stagnation point flow) to that obtained from an "impulsive start" where 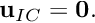${\bf u}_{IC} = {\bf 0}.$ (This is most easily implemented by replacing the call to set_initial_condition() with a call to Problem::assign_initial_values_impulsive().

Why do we obtain the same velocity with both initial conditions and why does the pressure take a few timesteps (How many exactly? Compare simulations with BDF<4> and BDF<2> timesteppers.) to "catch up" with the exact solution? [Hint: The unsteady stagnation point flow is a potential flow, therefore the viscous terms in the Navier-Stokes equations disappear. See also chapter 3.19 in Volume 2 of Gresho & Sani's wonderful book "Incompressible Flow and the Finite Element Method".]

Source files for this tutorial

The source files for this tutorial are located in the directory: demo_drivers/navier_stokes/osc_ellipse/
The driver code is: demo_drivers/navier_stokes/osc_ellipse/osc_quarter_ellipse.cc

PDF file

A pdf version of this document is available.