In this document we re-visit the collapsible channel problem yet again – this time to demonstrate the use of spatial adaptivity in fluid-structure interaction problems. In such problems, two additional issues have to be addressed:

We start with a brief reminder of oomph-lib's mesh adaptation procedures to highlight what additional complications arise in fluid-structure interaction problems, and then explain how these problems are addressed.

The assignment of positional history values for newly-created nodes

What is the problem?

We first discussed the use of spatial adaptivity for time-dependent problems in the context of the unsteady heat equation. We showed that whenever a new node is created, oomph-lib's mesh adaptation procedures automatically assign the nodal values and "history values" (the auxiliary values that are used by the Node's TimeStepper to approximate time-derivatives of the nodal values) for the newly-created Node by interpolating between the corresponding values in the new Node's father element.

Similarly, an initial assignment for the newly-created Node's current and previous positions (required for the evaluation of the mesh-velocities in the ALE formulation of the time-derivatives) is made by interpolating between the current and previous nodal positions of the new Node's father element. This default assignment is subsequently overwritten if the father element is associated with a MacroElement, in which case the newly-created Node's current position is determined by the father element's MacroElement representation. This ensures that the mesh refinement process respects curvilinear domain boundaries, as discussed
elsewhere. The same strategy is used to over-write the default assignment for a new Node's previous positions: They are re-assigned, based on the father element's MacroElement - representation, evaluated at the relevant previous timesteps.

To illustrate the process, consider the sketch below and assume that the time-integration of the Navier-Stokes equations is performed with a BDF<2> timestepper – a timestepper that requires two history values (the solution and the nodal positions at two previous timesteps) to evaluate the time-derivative $\partial u_i/\partial t$ in the momentum equations. The position of the nodes in the collapsible part of the channel is determined by the MacroElement - based representation of the CollapsibleChannelDomain, using the wall shape obtained from the compound MeshAsGeomObject that we created from the discretisation of the elastic wall, shown in green.

Assume that the initial mesh is sufficiently fine to resolve the solution at and $t=t_0 + \Delta t$ . At $t=t_0 + 2 \Delta t$ , the automatic mesh adaptation splits one of the fluid elements, creating the five new Nodes, shown in red (for simplicity we only show the fluid elements' vertex nodes). Their position is determined by the father element's MacroElement mapping, using the current position of the MeshAsGeomObject, obtained from the interpolation between the nodal positions of its SolidNodes (shown as green circles).

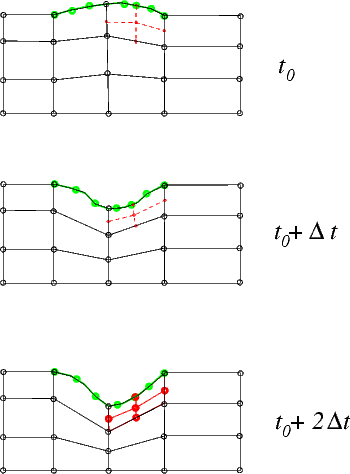
Sketch illustrating the assignment of positional history values for newly-created nodes in FSI problems. The positional history values of the newly-created Nodes (shown in red) are given by the positions they would have had if they had already existed at previous timesteps.

So far, so good! A subtle problem arises when we try to assign the positional history values for the newly-created Nodes. The evaluation of the MacroElement mapping at the previous timesteps (required to determine the positions the newly-created Nodes would have had, if they had already existed at previous timesteps) requires access to the previous wall shapes. In the non-FSI problem discussed earlier, the wall shape was given analytically and could therefore be evaluated at arbitrary times. In the FSI problem considered here, the previous wall shape is not available as the previous positions of the SolidNodes are not required (and are therefore not stored) for the solution of the (steady!) wall equations.

The solution: The Steady<NSTEPS> timestepper

The solution to the problem is simple: Recall that the final entry in the argument list of oomph-lib's mesh constructors specifies the TimeStepper to be used for the evaluation of any time-derivatives. The TimeStepper's member function TimeStepper::ntstorage() specifies the total number of values (the current value plus the number of history values) required to evaluate the time-derivatives; it is used by the FiniteElement::construct_node(...) function to create the required amount of storage at the elements' Nodes when the Nodes are created in the mesh constructor. To maximise the potential for code-reuse, we always provide a default argument for the pointer to the TimeStepper – a pointer to a static instantiation of oomph-lib's dummy TimeStepper, Steady<0>. This ensures that the "user" can use the mesh for steady problems without having to artificially create a dummy TimeStepper that would be completely irrelevant for his/her problem.

For instance, the full interface to the constructor of the OneDLagrangianMesh, defined in one_d_lagrangian_mesh.template.h is given by

    /// Constructor: Pass number of elements, length,
    /// pointer to GeomObject that defines the undeformed Eulerian position,
    /// and the timestepper -- defaults to (Steady) default timestepper defined
    /// in the Mesh base class
    OneDLagrangianMesh(
      const unsigned& n_element,
      const double& length,
      GeomObject* undef_eulerian_posn_pt,
      TimeStepper* time_stepper_pt = &Mesh::Default_TimeStepper);

Thus, when we constructed the wall mesh in the non-adaptive version of the driver code fsi_collapsible_channel.cc, using the statements

//Create the "wall" mesh with FSI Hermite beam elements
Wall_mesh_pt = new OneDLagrangianMesh<FSIHermiteBeamElement>
 (Ncollapsible,Lcollapsible,undeformed_wall_pt);

the use of the dummy TimeStepper, Steady<0> was implied. All time-derivatives computed by this TimeStepper evaluate to zero, and the TimeStepper does not require (or request) any storage for history values. This is a sensible default for problems that are either inherently steady (such as problems involving the Poisson equations, say) or for steady versions of time-dependent PDEs (such as the steady Navier-Stokes equations). In the present problem, we wish to retain the dummy character of the TimeStepper so that all time-derivatives in the FSIHermiteBeamElements are set to zero, while retaining a limited history of the SolidNode's previous positions so that the wall shape at previous timesteps can be evaluated. This is possible by creating a Steady timestepper with a non-zero template argument: The class

template<unsigned NSTEPS>

class Steady : public TimeStepper

provides a dummy TimeStepper that requires (and maintains) NSTEPS history values that represent the nodal positions (or nodal values) at NSTEPS previous timesteps. However, these history values are not used to evaluate any time-derivatives – all time-derivatives computed by this TimeStepper are zero.

If the Navier-Stokes equations are discretised with a BDF<2> timestepper, the evaluation of the mesh velocity in the ALE representation of the time-derivatives $\partial u_i/\partial t$ requires the nodal position at the two previous timesteps. This is achieved by passing a pointer to a specifically-constructed Steady<2> timestepper to the wall mesh. Here is the relevant code fragment from the Problem constructor in the driver code fsi_collapsible_channel_adapt.cc:

 // Allocate the timestepper for the Navier-Stokes equations
 BDF<2>* fluid_time_stepper_pt=new BDF<2>;
 
 // Add the fluid timestepper to the Problem's collection of timesteppers.
 add_time_stepper_pt(fluid_time_stepper_pt);
 
 // Create a dummy Steady timestepper that stores two history values
 Steady<2>* wall_time_stepper_pt = new Steady<2>;
 
 // Add the wall timestepper to the Problem's collection of timesteppers.
 add_time_stepper_pt(wall_time_stepper_pt);
 
 // Geometric object that represents the undeformed wall: 
 // A straight line at height y=ly; starting at x=lup.
 UndeformedWall* undeformed_wall_pt=new UndeformedWall(lup,ly);
 
 //Create the "wall" mesh with FSI Hermite beam elements, passing the
 //dummy wall timestepper to the constructor
 Wall_mesh_pt = new OneDLagrangianMesh<FSIHermiteBeamElement>
  (Ncollapsible,Lcollapsible,undeformed_wall_pt,wall_time_stepper_pt);

Updating the node-update data in refineable AlgebraicMeshes

When discussing the non-FSI version of the collapsible channel problem we explained how oomph-lib's mesh adaptation procedures assign the node-update data for newly-created AlgebraicNodes. Recall that the node-update data comprises:

A pointer to the AlgebraicMesh that implements the node-update function.
An ID for the node-update function. This is used in cases in which different regions of the AlgebraicMesh are updated by different node-update functions. The ID has a default value of 0; this is used if there is only a single node-update function, as in the AlgebraicCollapsibleChannelMesh.
A vector of (pointers to) GeomObjects that are involved in the node update.
A vector of reference values, such as the intrinsic coordinates of reference points on the GeomObjects.

By default, we assume that a newly-created AlgebraicNode is updated by the same node-update function as the AlgebraicNodes in its father element. Therefore we pass the pointer to the AlgebraicMesh, the node-update function ID, and the vector of pointers to GeomObjects to the newly-created AlgebraicNodes, and interpolate the reference values between those stored at the AlgebraicNodes in the father elements.

In most cases this provides a sensible default. For instance, it is hard to imagine a situation in which it would be sensible to update the position of newly-created AlgebraicNodes by a procedure that differs from that used for the surrounding AlgebraicNodes that already existed in the father element. Similarly, since the reference values vary from node to node (if they were constant we would not store them in the AlgebraicNodes' node-update data but in the AlgebraicMesh that implements the node update!) it makes sense to assign the values at newly-created AlgebraicNodes by interpolation. For instance, in the AlgebraicCollapsibleChannelMesh one of the reference values is the - coordinate of the reference point on the fixed lower wall. For the AlgebraicNodes that already existed in the coarse base mesh, this value is given by the the AlgebraicNodes' - coordinate in the undeformed mesh. Interpolation of this value for the newly-created AlgebraicNodes results in an axially uniform subdivision of the refined elements.

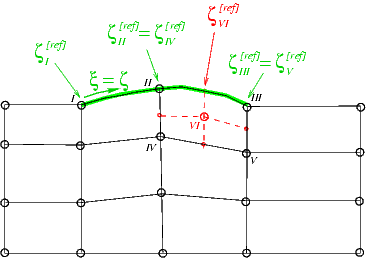
The same procedure may be used to assign the reference value that represents the intrinsic coordinate of the reference point on the upper wall – at least as long as the upper wall is only ever addressed as a compound GeomObject, as in our original (slow!) code that employed a MacroElement - based node update. The procedure is illustrated in the sketch below: The upper wall is parametrised by a compound GeomObject in which the beam's Lagrangian coordinate $\xi$ doubles as the GeomObject's intrinsic coordinate $\zeta.$ The green arrows indicate the reference points for nodes I, II, III, IV and V in the coarse initial mesh. The reference values $\zeta_{I}^{[ref]}, ... , \zeta_{V}^{[ref]}$ are stored in the node-update data of nodes I,...,V, respectively. The red arrow identifies the reference point for the newly-created node VI whose reference coordinate $\zeta_{IV}^{[ref]}$ is created by interpolation between the reference values of nodes II, III, IV and V, i.e. the nodes in its father element.

Illustration of the default update procedure for the node-update data: The reference value for newly created node VI is created by interpolation from the reference values for nodes II, III, IV and V in its father element.

Unfortunately, the default assignment is not appropriate for nodes that are updated by the (much faster) algebraic node update procedure implemented in the AlgebraicCollapsibleChannelMesh. Its AlgebraicNodes store pointers to the sub-GeomObjects (i.e. the FSIHermiteBeamElements in the wall mesh) that contain their reference points, and the values of the local coordinate at which the reference points are located. This is illustrated in the sketch below in which the sub- GeomObjects, parametrised by their local coordinates $s = \zeta,$ are shown in magenta. Note that the reference points for nodes II and IV are located in one sub- GeomObject, those for nodes III and V are located in another.

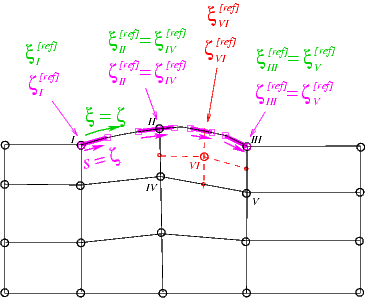
Illustration of the revised update procedure for the node-update data: The intrinsic coordinate within the compound GeomObject can be created by interpolation. The coordinate within the sub-GeomObject has to be determined via the GeomObject::locate_zeta(...) function.

It obviously does not make sense to create the reference value for the newly-created node VI by interpolation. The node update data must be created from scratch in two steps:

Determine the newly-created Node's intrinsic reference coordinate within the compound MeshAsGeomObject (i.e. the continuous beam's Lagrangian coordinate), $\xi_{VI}^{[ref]}$ by interpolation. (Recall that the AlgebraicNodes in the non-refineable AlgebraicCollapsibleChannelMesh already stored this coordinate, even though it was not used during the node-update itself).
Use the GeomObject::locate_zeta(...) function to determine sub-GeomObject and the local coordinate within it, at which the reference point with Lagrangian coordinate $\xi_{VI}^{[ref]}$ is located.

To ensure that this procedure is performed automatically after every mesh adaptation, it should be implemented in the function AlgebraicMesh::update_node_update(...). This function is defined as a pure virtual function in the AlgebraicMesh base class in order to force the mesh writer to assess if the default procedure for the assignment of the node-update data for newly-created AlgebraicNodes, described above, is appropriate. If it is, the function may, of course, be implemented as an empty function. We note that the function AlgebraicMesh::update_node_update(...) is called after the default values for the node-update data have been assigned. It is therefore only necessary to correct those values for which the default procedure is inappropriate.

To illustrate the procedure, here is the class definition for the RefineableAlgebraicCollapsibleChannelMesh. The mesh is derived by multiple inheritance from the non-refineable AlgebraicCollapsibleChannelMesh and the RefineableQuadMesh base class. The constructor calls the constructors of both underlying meshes and then sets up the QuadTreeForest:

  //=====start_of_refineable_algebraic_collapsible_channel_mesh=====
  /// Refineable version of the CollapsibleChannel mesh with
  /// algebraic node update.
  //=================================================================
  template<class ELEMENT>
  class RefineableAlgebraicCollapsibleChannelMesh
    : public RefineableQuadMesh<ELEMENT>,
      public virtual AlgebraicCollapsibleChannelMesh<ELEMENT>
  {
  public:
    /// Constructor: Pass number of elements in upstream/collapsible/
    /// downstream segment and across the channel; lengths of upstream/
    /// collapsible/downstream segments and width of channel, pointer to
    /// GeomObject that defines the collapsible segment and pointer to
    /// TimeStepper (defaults to the default timestepper, Steady).
    RefineableAlgebraicCollapsibleChannelMesh(
      const unsigned& nup,
      const unsigned& ncollapsible,
      const unsigned& ndown,
      const unsigned& ny,
      const double& lup,
      const double& lcollapsible,
      const double& ldown,
      const double& ly,
      GeomObject* wall_pt,
      TimeStepper* time_stepper_pt = &Mesh::Default_TimeStepper)
      : CollapsibleChannelMesh<ELEMENT>(nup,
                                        ncollapsible,
                                        ndown,
                                        ny,
                                        lup,
                                        lcollapsible,
                                        ldown,
                                        ly,
                                        wall_pt,
                                        time_stepper_pt),
        AlgebraicCollapsibleChannelMesh<ELEMENT>(nup,
                                                 ncollapsible,
                                                 ndown,
                                                 ny,
                                                 lup,
                                                 lcollapsible,
                                                 ldown,
                                                 ly,
                                                 wall_pt,
                                                 time_stepper_pt)
    {
      // Build quadtree forest
      this->setup_quadtree_forest();
    }

We overload the (empty) previous implementations of AlgebraicMesh::update_node_update(...) with our own function:

    /// Update the node update data for specified node following
    /// any mesh adapation
    void update_node_update(AlgebraicNode*& node_pt);
  };

Here is the actual implementation of this function. We start by extracting the reference values that were already assigned by the default procedure:

  //========start_update_node_update=================================
  /// Update the geometric references that are used
  /// to update node after mesh adaptation.
  //=================================================================
  template<class ELEMENT>
  void RefineableAlgebraicCollapsibleChannelMesh<ELEMENT>::update_node_update(
    AlgebraicNode*& node_pt)
  {
    // Extract reference values for node update by copy construction
    Vector<double> ref_value(node_pt->vector_ref_value());

Recall from the discussion of the algebraic node-update strategy for the non-refineable version of the problem that reference values 0 and 1 store the - coordinate along the fixed bottom wall, and the fractional height of the node in the cross-channel direction, respectively. These values are interpolated correctly and do not have to be corrected. The third reference value is the intrinsic coordinate of the reference point in its sub-GeomObject. This needs to be re-computed and we will assign the corrected value below. The fourth reference value is the intrinsic coordinate of the reference point within the compound MeshAsGeomObject. We store this in a temporary variable:

    // Fourth reference value: intrinsic coordinate on the (possibly
    // compound) wall.
    double zeta = ref_value[3];

Next, we extract vector of (pointers to the) GeomObjects involved in this node's node-update from the node.

// Extract geometric objects for update by copy construction

Vector<GeomObject*> geom_object_pt(node_pt->vector_geom_object_pt());

Now we use the GeomObject::locate_zeta(...) function to obtain the pointer to the (sub-)GeomObject and the intrinsic coordinate within it, at which the reference point (identified by its intrinsic coordinate zeta in the compound GeomObject) is located:

    // Get pointer to geometric (sub-)object and Lagrangian coordinate
    // on that sub-object. For a wall that is represented by
    // a single geom object, this simply returns the input.
    // If the geom object consists of sub-objects (e.g.
    // if it is a finite element mesh representing a wall,
    // then we'll obtain the pointer to the finite element
    // (in its incarnation as a GeomObject) and the
    // local coordinate in that element.
    Vector<double> s(1);
    GeomObject* geom_obj_pt;
    this->Wall_pt->locate_zeta(zeta_wall, geom_obj_pt, s);

We over-write the first (and, in fact, only) entry in the vector of GeomObjects that are involved in this node's node-update with the pointer to the (sub-)GeomObject just located:

    // Update the pointer to the (sub-)GeomObject within which the
    // reference point is located. (If the wall is simple GeomObject
    // this is the same as Wall_pt; if it's a compound GeomObject
    // this points to the sub-object)
    geom_object_pt[0] = geom_obj_pt;

Similarly, we over-write the third reference value with the local coordinate of the reference point within its (sub-)GeomObject.

    // Update third reference value: Reference local coordinate
    // in wall element (local coordinate in FE if we're dealing
    // with a wall mesh)
    ref_value[2] = s[0];

The incorrect entries in the two vectors geom_object_pt and ref_value have now been corrected. We can wipe the node's node-update data and re-assign it:

    // Kill the existing node update info
    node_pt->kill_node_update_info();
 
    // Setup algebraic update for node: Pass update information
    node_pt->add_node_update_info(this, // mesh
                                  geom_object_pt, // vector of geom objects
                                  ref_value); // vector of ref. values
  }

That's it!

Results

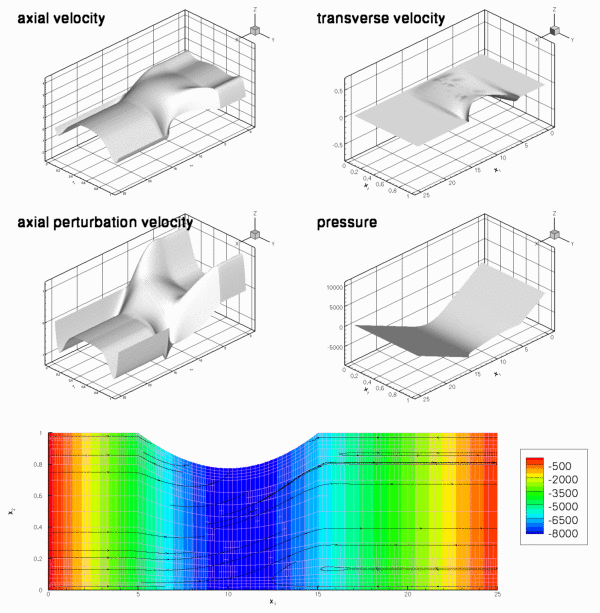
The figure below shows a snapshot of the flow field during the early stages of the oscillation. The computation was performed with refineable Crouzeix-Raviart elements, using the RefineableAlgebraicCollapsibleChannelMesh. Note how the automatic mesh adaptation has refined the mesh in the regions in which the Stokes layers create steep velocity gradients.

Snapshot from the animation of the flow field.

The driver code

The driver code fsi_collapsible_channel_adapt.cc for the spatially adaptive problem is a trivial extension of the non-adaptive code fsi_collapsible_channel.cc, therefore we will not provide a detailed listing here. Comparing the two source codes (e.g. with sdiff) shows that spatial adaptivity may be enabled with a few straightforward changes:

Change the fluid mesh from the MacroElementNodeUpdateCollapsibleChannelMesh to the MacroElementNodeUpdateRefineableCollapsibleChannelMesh (or from the AlgebraicCollapsibleChannelMesh to the RefineableAlgebraicCollapsibleChannelMesh).
Change the element type from TaylorHoodElement<2> to RefineableQTaylorHoodElement<2> (or QCrouzeixRaviartElement<2> to RefineableQCrouzeixRaviartElement<2>).
Add the functions Problem::actions_before_adapt() and Problem::actions_after_adapt(); see below.
Explicitly specify the Steady<2> timestepper for the wall mesh, as discussed above.
Create an error estimator, specify the target errors for the adaptation, and call the spatially adaptive Newton solver.

Actions before and after solve

As in the non-FSI problem, we use the function Problem::actions_before_adapt() to delete the applied traction elements before the mesh adaptation:

//=========start_of_actions_before_adapt==================================
/// Actions before adapt: Wipe the mesh of prescribed traction elements
//========================================================================
template<class ELEMENT>
void FSICollapsibleChannelProblem<ELEMENT>::actions_before_adapt()
{
 // Kill the traction elements and wipe surface mesh
 delete_traction_elements(Applied_fluid_traction_mesh_pt);
 
 // Rebuild the global mesh. 
 rebuild_global_mesh();
 
} // end of actions_before_adapt

As usual, we then employ the function Problem::actions_after_adapt() to re-attach traction elements to the fluid elements that are located at the mesh's inflow boundary (mesh boundary 5) when the mesh adaptation is complete.

//==========start_of_actions_after_adapt==================================
/// Actions after adapt: Rebuild the mesh of prescribed traction elements
//========================================================================
template<class ELEMENT>
void FSICollapsibleChannelProblem<ELEMENT>::actions_after_adapt()
{
 // Create prescribed-flux elements from all elements that are 
 // adjacent to boundary 5 and add them to surface mesh
 create_traction_elements(5,Bulk_mesh_pt,Applied_fluid_traction_mesh_pt);
 
 // Rebuild the global mesh
 rebuild_global_mesh();

Next, we pin the redundant pressure degrees of freedom (see another tutorial for details) and pass the function pointer to the function that defines the prescribed traction to the applied traction elements:

 
 // Unpin all pressure dofs
 RefineableNavierStokesEquations<2>::
  unpin_all_pressure_dofs(Bulk_mesh_pt->element_pt());
 
 // Pin redundant pressure dofs
 RefineableNavierStokesEquations<2>::
  pin_redundant_nodal_pressures(Bulk_mesh_pt->element_pt());
   
 // Loop over the traction elements to pass pointer to prescribed 
 // traction function
 unsigned n_element=Applied_fluid_traction_mesh_pt->nelement();
 for(unsigned e=0;e<n_element;e++)
  {
   // Upcast from GeneralisedElement to NavierStokesTractionElement element
   NavierStokesTractionElement<ELEMENT> *el_pt = 
    dynamic_cast<NavierStokesTractionElement<ELEMENT>*>(
     Applied_fluid_traction_mesh_pt->element_pt(e));
   
   // Set the pointer to the prescribed traction function
   el_pt->traction_fct_pt() = &Global_Physical_Variables::prescribed_traction;
  }

We specify the function FSI_functions::apply_no_slip_on_moving_wall() as the auxiliary node-update function for all fluid nodes that are located on the FSI boundary (mesh boundary 3) – this ensures that the fluid velocity is updated (via the no-slip condition) whenever the position of a fluid node on this boundary is updated. For fluid nodes that already existed before the mesh adaptation this statement over-writes the function pointers already stored at those nodes. Note the use of compiler flags to distinguish between the two node-update strategies.

 
 // The functions used to update the no slip boundary conditions 
 // must be set on any new nodes that have been created during the 
 // mesh adaptation process. 
 // There is no mechanism by which auxiliary update functions 
 // are copied to newly created nodes.
 // (because, unlike boundary conditions, they don't occur exclusively 
 // at boundaries)
 
 // The velocity of the fluid nodes on the wall (fluid mesh boundary 3)
 // is set by the wall motion -- hence the no-slip condition needs to be
 // re-applied whenever a node update is performed for these nodes. 
 // Such tasks may be performed automatically by the auxiliary node update 
 // function specified by a function pointer:
 unsigned ibound=3; 
 unsigned num_nod= bulk_mesh_pt()->nboundary_node(ibound);
 for (unsigned inod=0;inod<num_nod;inod++)
  {
   bulk_mesh_pt()->boundary_node_pt(ibound, inod)->
    set_auxiliary_node_update_fct_pt(
     FSI_functions::apply_no_slip_on_moving_wall);
  }

Finally, we re-generate the FSI lookup scheme that establishes which fluid elements are located next to the Gauss points in the beam elements. This is necessary because the previous lookup scheme, set up in the problem constructor, becomes invalid if any of the fluid elements next the wall are split during the refinement process.

 
 // (Re-)setup fsi: Work out which fluid dofs affect wall elements
 // the correspondance between wall dofs and fluid elements is handled
 // during the remeshing, but the "reverse" association must be done
 // separately. We need to set up the interaction every time because the fluid
 // element adjacent to a given solid element's integration point may have 
 // changed.We pass the boundary between the fluid and solid meshes and 
 // pointers to the meshes. The interaction boundary is boundary 3 of 
 // the Fluid mesh.
 FSI_functions::setup_fluid_load_info_for_solid_elements<ELEMENT,2>
  (this,3,Bulk_mesh_pt,Wall_mesh_pt);
 
 
} // end of actions_after_adapt

Comments and Exercises

Exercises

The post-processing function doc_solution(...) outputs the wall shape at the present and the two previous timesteps: The output file walli-j.dat is created at the i - th timestep and contains the wall shape at the j - th previous timestep. To check that the Steady<2> timestepper correctly maintains the time-history of the wall displacement field, confirm that wall3-2.dat is identical to wall2-0.dat, say.
Explore what happens if the Steady<2> timestepper is not specified explicitly. [Hint: Unless you have compiled the library with -DRANGE_CHECKING, the code will die with a segmentation fault – use the debugger to determine where the segmentation fault occurs and explain what goes wrong.]
Explain why refineable MacroElementNodeUpdateMeshes do not require a update_node_update() function.
Explore what happens if the empty function AlgebraicCollapsibleChannelMesh::update_node_update(...) is not overloaded in the derived refineable mesh RefineableAlgebraicCollapsibleChannelMesh. [Hint: Inspect the plot of the initial conditions in the output file soln0.dat to see how the uniform refinement performed in the problem constructor fails if the function RefineableAlgebraicCollapsibleChannelMesh::update_node_update(...) is not executed.]

Source files for this tutorial

The source files for this tutorial are located in the directory:

demo_drivers/interaction/fsi_collapsible_channel/
The driver code is:

demo_drivers/interaction/fsi_collapsible_channel/fsi_collapsible_channel_adapt.cc

PDF file

A pdf version of this document is available.