In this example we demonstrate the solution of the 2D linear wave equation – a hyperbolic PDE that involves second time-derivatives. Timestepping of such problems may be performed with timesteppers from the Newmark family. We demonstrate their use and illustrate how to assign the initial conditions.

The example problem

We shall illustrate the timestepping procedures for hyperbolic problems by considering the solution of the 2D linear wave equation in a rectangular domain:

The two-dimensional linear wave equation in a rectangular domain. Solve

$\sum_{i=1}^2\frac{\partial^2 u}{\partial x_i^2} = \frac{\partial^2 u}{\partial t^2} + f\left(x_1,x_2,t\right), \ \ \ \ \ \ \ \ \ \ (1)$

in the rectangular domain $D = \left\{ (x_1,x_2) \ \bigg| \ x_1 \in [0,1],\ x_2 \in [0,2] \right\}$ , subject to the Dirichlet boundary conditions

$\left. u\right|_{\partial D}=g_0 \ \ \ \ \ \ \ \ \ \ (2)$

and the initial conditions

$u(x_1,x_2,t=0)=h_0(x_1,x_2), \ \ \ \ \ \ \ \ \ \ (3)$

and

$\left. \frac{\partial u}{\partial t}\right|_{t=0}=k_0(x_1,x_2), \ \ \ \ \ \ \ \ \ \ (4)$

where the functions

and

are given.

Here we consider the unforced case, , and choose boundary and initial conditions that are consistent with the exact, travelling-wave solution

$u_0(x_1,x_2,t) = \tanh\left(1-\alpha\left(\zeta-t\right)\right), \ \ \ \ \ \ \ \ \ \ (5)$

where

$\zeta=\cos\left(\phi\right)x_1+\sin\left(\phi\right)x_2, \ \ \ \ \ \ \ \ \ \ (6)$

is the travelling-wave coordinate. The solution represents a tanh step profile that propagates with unit speed through the domain. The parameter $\alpha$ controls the steepness of the step while $\phi$ controls the orientation of the step in the - plane.

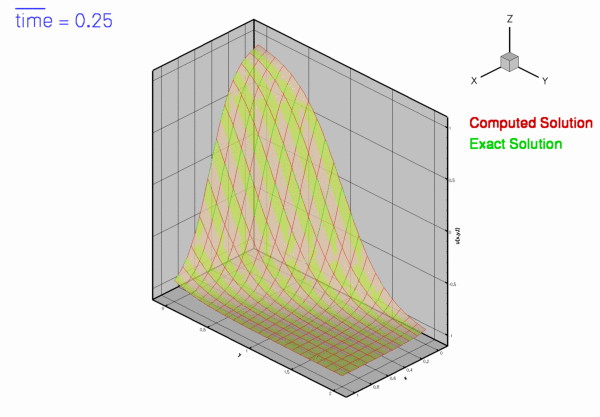
The figure below shows a plot of computed and exact solutions at time , for a steepness parameter $\alpha=4$ , and an angle $\phi=\pi/6$ . The plot is a snapshot, taken from the animation of the solution.

Snapshot of the exact and computed solutions.

Global parameters and functions

As usual, we store the problem parameters in a namespace. Note that we define not only the exact solution but also its first and second time-derivatives, as both are needed to assign the initial conditions for the Newmark timestepper; see Setting the initial conditions for Newmark timesteppers for details.

//==start_of_tanh_solution============================================
/// Namespace for exact solution for LinearWave equation 
/// with sharp step 
//====================================================================
namespace TanhSolnForLinearWave
{
 
 /// Parameter for steepness of step
 double Alpha;
 
 /// Orientation of step wave
 double Phi;
 
 /// Exact solution
 double exact_u(const double& time, const Vector<double>& x)
 {
  double zeta=cos(Phi)*x[0]+sin(Phi)*x[1];
  return tanh(1.0-Alpha*(zeta-time));
 }
 
 /// 1st time-deriv of exact solution
 double exact_dudt(const double& time, const Vector<double>& x)
 {
  double zeta=cos(Phi)*x[0]+sin(Phi)*x[1];
  return Alpha/(cosh(1.0-Alpha*(zeta-time))*
              cosh(1.0-Alpha*(zeta-time)));
 }
 
 /// 2nd time-deriv of exact solution
 double exact_d2udt2(const double& time, const Vector<double>& x)
 {
  double zeta=cos(Phi)*x[0]+sin(Phi)*x[1];
  return -2.0*Alpha*Alpha*tanh(1.0-Alpha*(zeta-time))/
   (cosh(1.0-Alpha*(zeta-time))*cosh(1.0-Alpha*(zeta-time)));
 }
 
 
 /// Exact solution as a vector
 void get_exact_u(const double& time, const Vector<double>& x, 
                  Vector<double>& u)
 {
  u[0]=exact_u(time,x);
  u[1]=exact_dudt(time,x);
  u[2]=exact_d2udt2(time,x);
 }
 
 /// Source function to make it an exact solution 
 void get_source(const double& time, const Vector<double>& x, double& source)
 {
  source=0.0;
 }
 
} // end of tanh solution

The driver code

As in most previous time-dependent example codes, we use the command line arguments as flags that indicate if the code is run in validation mode – if command line arguments are specified, the code will only perform a small number of timesteps.

//===start_of_main========================================================
/// Demonstrate how to solve LinearWave problem.
//========================================================================
int main(int argc, char* argv[])
{
 
 // Store command line arguments: If a command line argument is specied
 // we regard this as validation run.
 CommandLineArgs::setup(argc,argv);

We build the problem with 2D bi-quadratic QLinearWaveElements and a Newmark<1> timestepper (see Setting the initial conditions for Newmark timesteppers for an explanation of the template argument), passing the number of elements, and the pointer to the source function to the constructor, and run the time time-dependent simulation. We solve the problem twice, once with an impulsive start and once a with "smooth" start from the travelling-wave solution (5).

 
 // Number of elements in x direction
 unsigned n_x=10;
 
 // Number of elements in y direction
 unsigned n_y=20;
 
 // Impulsive start?
 bool impulsive_start;
 
 // Run with impulsive start
 // ------------------------
 {
  impulsive_start=true;
 
  // Build problem
  LinearWaveProblem<QLinearWaveElement<2,3>, Newmark<1> >
   problem(n_x,n_y,impulsive_start,&TanhSolnForLinearWave::get_source);
  
  // Run it
  problem.unsteady_run();
 }
 
 // Run with "smooth" start
 // -----------------------
 {
  impulsive_start=false;
 
  // Build problem
  LinearWaveProblem<QLinearWaveElement<2,3>, Newmark<1> >
   problem(n_x,n_y,impulsive_start,&TanhSolnForLinearWave::get_source);
  
  // Run it
  problem.unsteady_run();
 }
 
 
}; // end of main

The problem class

The problem class is practically identical to that used for the corresponding unsteady heat problem. No actions are required before or after the solve but the time-dependent boundary conditions must be updated before every timestep.

//===start_of_problem_class===========================================
/// LinearWave problem in rectanglular domain
//====================================================================
template<class ELEMENT, class TIMESTEPPER>
class LinearWaveProblem : public Problem
{
 
public:
 
 /// Constructor: pass number of elements in x and y directions,
 /// bool indicating impulsive or "smooth" start,
 /// and pointer to source function
 LinearWaveProblem(const unsigned& nx, const unsigned& ny, 
                   const bool& impulsive_start,
                   LinearWaveEquations<2>::LinearWaveSourceFctPt source_fct_pt);
 
 /// Destructor (empty) 
 ~LinearWaveProblem() {}
 
 /// Update the problem specs after solve (empty)
 void actions_after_newton_solve() {}
 
 /// Update the problem specs before solve (empty)
 void actions_before_newton_solve() {}
 
 /// Update the problem specs after solve (empty)
 void actions_after_implicit_timestep() {}
 
 /// Update the problem specs before next timestep: 
 /// Set time-dependent Dirchlet boundary from exact solution.
 void actions_before_implicit_timestep()
  {
   Vector<typename TIMESTEPPER::NodeInitialConditionFctPt> 
    initial_value_fct(1);
   Vector<typename TIMESTEPPER::NodeInitialConditionFctPt>
    initial_veloc_fct(1);
   Vector<typename TIMESTEPPER::NodeInitialConditionFctPt> 
    initial_accel_fct(1);
   
   // Assign values for analytical value, veloc and accel:
   initial_value_fct[0]=&TanhSolnForLinearWave::exact_u;
   initial_veloc_fct[0]=&TanhSolnForLinearWave::exact_dudt;
   initial_accel_fct[0]=&TanhSolnForLinearWave::exact_d2udt2;
   
   // Loop over boundaries
   unsigned num_bound=mesh_pt()->nboundary();
   for (unsigned ibound=0;ibound<num_bound;ibound++)
    {
     // Loop over boundary nodes
     unsigned num_nod=mesh_pt()->nboundary_node(ibound);
     for (unsigned inod=0;inod<num_nod;inod++)
      {
       // Set the boundary condition from the exact solution
       Node* nod_pt=mesh_pt()->boundary_node_pt(ibound,inod);
 
       bool use_direct_assignment=false;
       if (use_direct_assignment)
        {
         // Set nodal coordinates for evaluation of BC:
         Vector<double> x(2);
         x[0]=nod_pt->x(0);
         x[1]=nod_pt->x(1);
         
         // Set exact solution at current time
         nod_pt->set_value(0,
                           TanhSolnForLinearWave::exact_u(time_pt()->time(),x));
        }
       else
        {
         // Get timestepper
         TIMESTEPPER* timestepper_pt=dynamic_cast<TIMESTEPPER*>
          (time_stepper_pt());
         
         // Assign the history values
         timestepper_pt->assign_initial_data_values(nod_pt, 
                                                    initial_value_fct,
                                                    initial_veloc_fct,
                                                    initial_accel_fct);
        }
      }
    }
  } // end of actions before timestep
 
 ///  Set initial condition (incl history values)
 void set_initial_condition();
 
 /// Doc the solution
 void doc_solution(DocInfo& doc_info);
 
 /// Do unsteady run 
 void unsteady_run();
 
private:
 
 // Trace file
 ofstream Trace_file;
 
 // Impulsive start?
 bool Impulsive_start;
 
}; // end of problem class

The problem constructor

The problem constructor is also fairly standard: We start by creating the timestepper (of the type specified by the template argument), pass it to the Problem's collection of timesteppers, and initialise the parameters for the exact solution.

//===start_of_constructor=================================================
/// Constructor for LinearWave problem 
//========================================================================
template<class ELEMENT, class TIMESTEPPER>
LinearWaveProblem<ELEMENT,TIMESTEPPER>::LinearWaveProblem(
 const unsigned& nx, const unsigned& ny, const bool& impulsive_start, 
 LinearWaveEquations<2>::LinearWaveSourceFctPt source_fct_pt) :
 Impulsive_start(impulsive_start)
{ 
 
 //Allocate the timestepper -- this constructs the time object as well
 add_time_stepper_pt(new TIMESTEPPER());
 
 // Set up parameters for exact solution
 //-------------------------------------
 
 // Steepness of tanh profile
 TanhSolnForLinearWave::Alpha=4.0;
 
 // Orientation of step wave
 TanhSolnForLinearWave::Phi=MathematicalConstants::Pi/180.0*30.0;

Next, we build the mesh and pin the nodal values on the Dirichlet boundaries (i.e. at all boundary nodes). Recall that the pointer to the timestepper must be passed the mesh constructor to allow the creation of Nodes that provide sufficient storage for the "history values" required by the timestepper.

 
 // Set up mesh
 //------------
 
 // # of elements in x-direction
 unsigned Nx=nx;
 
 // # of elements in y-direction
 unsigned Ny=ny;
 
 // Domain length in x-direction
 double Lx=1.0;
 
 // Domain length in y-direction
 double Ly=2.0;
 
 // Build and assign mesh
 Problem::mesh_pt()=new RectangularQuadMesh<ELEMENT>(
  Nx,Ny,Lx,Ly,time_stepper_pt());
 
 // Set the boundary conditions for this problem: All nodes are
 // free by default -- just pin the ones that have Dirichlet conditions
 // here. 
 unsigned num_bound = mesh_pt()->nboundary();
 for(unsigned ibound=0;ibound<num_bound;ibound++)
  {
   unsigned num_nod= mesh_pt()->nboundary_node(ibound);
   for (unsigned inod=0;inod<num_nod;inod++)
    {
     mesh_pt()->boundary_node_pt(ibound,inod)->pin(0); 
    }
  } //end of boundary conditions

Finally, we complete the build of the elements by passing the pointer to the source function to the elements, and set up the equation numbering scheme.

 
 // Complete build of elements
 // --------------------------
 
 // Loop over the elements to set up element-specific 
 // things that cannot be handled by constructor 
unsigned n_element = mesh_pt()->nelement();
for(unsigned i=0;i<n_element;i++)
  {
   // Upcast from GeneralisedElement to the present element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(i));
 
   //Set the source function pointer
   el_pt->source_fct_pt() = source_fct_pt;
  }
 
 // Setup equation numbering scheme
 cout <<"Number of equations: " << assign_eqn_numbers() << std::endl; 
 
} // end of constructor

Setting the initial conditions for Newmark timesteppers

Most of the code discussed so far was (and most of what follows is) practically identical to that in the corresponding unsteady heat example. The main difference between the two example codes is the way in which the initial conditions are applied. This is closely related to the different role of the "history values" in BDF and Newmark timestepping schemes:

The interpretation of history values in BDF and Newmark timesteppers

In problems in which first time-derivatives are discretised by BDF timesteppers, the "history values" represent the values of the solution at previous timesteps, i.e. for a Data object that is associated with a timestepper from the BDF family, Data::value(t,i) returns the i-th value stored in the Data object, at the t-th previous timestep. We recall that when assigning initial conditions for computations with higher-order timesteppers from the BDF family, the number of (mathematical) initial conditions (the solution at the intial time, , say) is smaller than the number of "history values" required by the timestepper. For instance, a computation with a BDF<2> timestepper and a timestep dt not only requires the solution at but also the solution at $t=t_0- {\tt dt}$ . In most of our examples, this did not cause any problems. We either started the simulation with an "impulsive start" by setting all history values to the solution at , or we assigned the history values from an explicitly-given function (usually an exact solution of the governing equations), in which case the evaluation of the history values at previous timesteps was trivial.

Timesteppers from the Newmark family compute second-order accurate approximations for the first and second time-derivatives of the values stored in an associated Data object. Newmark timesteppers are implicit, single-step schemes since the approximation of the time-derivatives only involves quantities evaluated at the current time (where the solution is unknown) and at a single previous timestep. To facilitate their application in multiphysics problems where parts of a Problem might be discretised by timesteppers from the BDF family, say, Newmark timesteppers can allocate additional storage for the solution at the previous NSTEPS timesteps. These history values are stored in the Data objects and are updated by the timestepper when the solution is advanced to the next time level, but they are not used in the computation of the time-derivatives.

For a Data object that is associated with a Newmark<NSTEPS> timestepper, the history value obtained from Data::value(t,i) may be interpreted as follows:

t=0: The i-th value at at present time, Time_pt->time()
t=1: The i-th value at the previous timestep, Time_pt->time()-dt
...
t=NSTEPS: The i-th value at the NSTEPS-th previous timestep, i.e. at Time_pt->time()-NSTEPS*dt if the timestep dt was kept constant.
t=NSTEPS+1: The 1st time derivative (= "the velocity") of the i-th value at the previous timestep, Time_pt->time()-dt
t=NSTEPS+2: The 2nd time derivative (= "the acceleration") of the i-th value at the previous timestep, Time_pt->time()-dt.

The Newmark<1> timestepper is equivalent to the classical Newmark scheme.

Assigning the history values for Newmark timesteppers

The Newmark timestepper provides a number of helper functions that facilitate the assignment of "history values".

Impulsive starts:

Given a pointer, data_pt, to a Data object, the function Newmark<NSTEPS>::assign_initial_values_impulsive(data_pt) assigns history values that are consistent with an impulsive start from the Data object's current values.
"Smooth" starts from explicitly given time-histories:

If the solution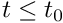 and its first and second time-derivatives are available analytically for 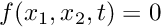$t \le t_0$ , the function Newmark<NSTEPS>::assign_initial_data_values(...) may be used to assign history values that are consistent
with this time history. Note that, as in the case of the higher-order BDF timesteppers, we require more information than is provided by the (mathematical) initial conditions which only provide the value and the first time-derivative of the unknown function at the initial time.

Implementation in the demo code

The function set_initial_condition() demonstrates the use of these functions in our example problem. The assignment of the "history values" for the nodal Data is handled by the timestepper, a pointer to which can be obtained from the Problem:

//===start_of_set_initial_condition=======================================
/// Set initial condition.
//========================================================================
template<class ELEMENT, class TIMESTEPPER>
void LinearWaveProblem<ELEMENT,TIMESTEPPER>::set_initial_condition()
{ 
 
 // Get timestepper
 TIMESTEPPER* timestepper_pt=dynamic_cast<TIMESTEPPER*>(time_stepper_pt());

To start the simulation with an impulsive start from the travelling-wave solution, defined in the namespace TanhSolnForLinearWave, we loop over all nodes and determine their positions. We then compute the value of the exact solution at that point and assign it to the current nodal value. "History values" that correspond to an impulsive start from this value are then assigned by calling Newmark<NSTEPS>::assign_initial_values_impulsive(...).

 
 
 // Impulsive start
 //----------------
 if (Impulsive_start)
  {
   // Loop over the nodes to set initial conditions everywhere
   unsigned num_nod=mesh_pt()->nnode();
   for (unsigned jnod=0;jnod<num_nod;jnod++)
    {
     // Pointer to node
     Node* nod_pt=mesh_pt()->node_pt(jnod);
 
     // Get nodal coordinates
     Vector<double> x(2);
     x[0]=nod_pt->x(0);
     x[1]=nod_pt->x(1);
 
     // Assign initial value from exact solution
     nod_pt->set_value(0,TanhSolnForLinearWave::exact_u(time_pt()->time(),x));
 
     // Set history values so that they are consistent with an impulsive
     // start from this value
     timestepper_pt->assign_initial_values_impulsive(nod_pt);
    }
  } // end impulsive start

To start the simulation with a "smooth" start from the travelling-wave solution we have to pass function pointers to the functions that specify the function and its first and second time-derivatives to Newmark<NSTEPS>::assign_initial_data_values(...). As usual, the required form of the function pointer is defined as a public typedef in the Newmark class. Since Data objects can store multiple values, each of which will generally have a different time-history, Newmark<NSTEPS>::assign_initial_data_values(...) expects a vector of function pointers. In the current example where each node only stores a single value, these vectors only have a single entry.

 
 // "Smooth" start from analytical time history
 //--------------------------------------------
 else
  {
 
   // Vector of function pointers to functions that specify the
   // value, and the first and second time-derivatives of the
   // function used as the initial condition
   Vector<typename TIMESTEPPER::NodeInitialConditionFctPt> 
    initial_value_fct(1);
   Vector<typename TIMESTEPPER::NodeInitialConditionFctPt>
    initial_veloc_fct(1);
   Vector<typename TIMESTEPPER::NodeInitialConditionFctPt> 
    initial_accel_fct(1);
   
   // Assign values for analytical value, veloc and accel:
   initial_value_fct[0]=&TanhSolnForLinearWave::exact_u;
   initial_veloc_fct[0]=&TanhSolnForLinearWave::exact_dudt;
   initial_accel_fct[0]=&TanhSolnForLinearWave::exact_d2udt2;

Now we loop over all nodes and pass the vectors of function pointers
to Newmark<NSTEPS>::assign_initial_data_values(...) to assign the required history values.

   
   // Assign Newmark history values so that Newmark approximations
   // for velocity and accel are correct at initial time:
 
   // Loop over the nodes to set initial conditions everywhere
   unsigned num_nod=mesh_pt()->nnode();
   for (unsigned jnod=0;jnod<num_nod;jnod++)
    {
     // Pointer to node
     Node* nod_pt=mesh_pt()->node_pt(jnod);
    
     // Assign the history values
     timestepper_pt->assign_initial_data_values(nod_pt, 
                                                initial_value_fct,
                                                initial_veloc_fct,
                                                initial_accel_fct);
    } // end of smooth start

To check/demonstrate that the assignment of the initial condition was successful, we compare the Newmark approximation for the zero-th, first and second time-derivatives of the nodal values against the exact solution and document the maximum discrepancy.

 
 
   // Paranoia: Check that the initial values were assigned correctly
   double err_max=0.0;
   for (unsigned jnod=0;jnod<num_nod;jnod++)
    {
     // Pointer to node
     Node* nod_pt=mesh_pt()->node_pt(jnod);
 
     // Get nodal coordinates
     Vector<double> x(2);
     x[0]=nod_pt->x(0);
     x[1]=nod_pt->x(1);
 
     // Get exact value and first and second time-derivatives
     double u_exact=
      TanhSolnForLinearWave::exact_u(time_pt()->time(),x);
     double dudt_exact=
      TanhSolnForLinearWave::exact_dudt(time_pt()->time(),x);
     double d2udt2_exact=
      TanhSolnForLinearWave::exact_d2udt2(time_pt()->time(),x);
    
     // Get Newmark approximations for zero-th, first and second 
     // time-derivatives of the nodal values. 
     double u_fe=timestepper_pt->time_derivative(0,nod_pt,0);
     double dudt_fe=timestepper_pt->time_derivative(1,nod_pt,0);
     double d2udt2_fe=timestepper_pt->time_derivative(2,nod_pt,0);
     
     // Error
     double error=sqrt(pow(u_exact-u_fe,2)+
                       pow(dudt_exact-dudt_fe,2)+
                       pow(d2udt2_exact-d2udt2_fe,2));
     if (error>err_max) err_max=error;
    }
   cout << "Max. error in assignment of initial condition " 
        << err_max << std::endl;   
  }
 
 
} // end of set initial condition

Post processing

The post-processing routine is practically identical to that in the corresponding unsteady heat example. We output the solution, and compare the computed and exact solutions.

 
 
 
//===start_of_doc_solution================================================
/// Doc the solution
//========================================================================
template<class ELEMENT, class TIMESTEPPER>
void LinearWaveProblem<ELEMENT,TIMESTEPPER>::doc_solution(DocInfo& doc_info)
{ 
 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned npts;
 npts=5; 
 
 cout << std::endl;
 cout << "=================================================" << std::endl;
 cout << "Docing solution for t=" << time_pt()->time() << std::endl;
 cout << "=================================================" << std::endl;
 
 // Output solution 
 //-----------------
 sprintf(filename,"%s/soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 mesh_pt()->output(some_file,npts);
 some_file << "TEXT X=2.5,Y=93.6,F=HELV,HU=POINT,C=BLUE,H=26,T=\"time = " 
           << time_pt()->time() << "\"";
 some_file << "GEOMETRY X=2.5,Y=98,T=LINE,C=BLUE,LT=0.4" << std::endl;
 some_file << "1" << std::endl;
 some_file << "2" << std::endl;
 some_file << " 0 0" << std::endl;
 some_file << time_pt()->time()*20.0 << " 0" << std::endl;
 some_file.close();
 
 // Output exact solution 
 //----------------------
 sprintf(filename,"%s/exact_soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 oomph_info << " FILENAME: " << filename << std::endl;
 some_file.open(filename);
 mesh_pt()->output_fct(some_file,npts,time_pt()->time(),
                        TanhSolnForLinearWave::get_exact_u); 
 some_file.close();
 
 // Doc error
 //----------
 double error,norm;
 sprintf(filename,"%s/error%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 mesh_pt()->compute_error(some_file,
                          TanhSolnForLinearWave::get_exact_u,
                          time_pt()->time(),
                          error,norm); 
 some_file.close();
 cout << "error: " << error << std::endl; 
 cout << "norm : " << norm << std::endl << std::endl;
 
 // Write trace file
 Trace_file << time_pt()->time() << " " << time_pt()->dt()
            << " " << mesh_pt()->nelement() << " " 
            << error << " " << norm << std::endl;
 
} // end of doc solution

The timestepping loop

Timestepping the linear wave equation involves exactly the same steps as in the unsteady heat example: We start by creating a DocInfo object to specify the output directories and open the trace file in which we record the time-evolution of the error.

//===start_of_unsteady_run================================================
/// Unsteady run.
//========================================================================
template<class ELEMENT, class TIMESTEPPER>
void LinearWaveProblem<ELEMENT,TIMESTEPPER>::unsteady_run()
{
 
 // Setup labels for output
 DocInfo doc_info;
 
 // Output directory
 if (Impulsive_start)
  {
   doc_info.set_directory("RESLT_impulsive"); 
  }
 else
  {
   doc_info.set_directory("RESLT_smooth"); 
  }
 
 // Open trace file
 char filename[100];   
 sprintf(filename,"%s/trace.dat",doc_info.directory().c_str());
 Trace_file.open(filename);

We then initialise the time, set the initial condition and output the initial solution.

 
 // Initialise time
 double time0=0.0;
 time_pt()->time()=time0;
 
 // Set initial timestep
 double dt=0.005;
 time_pt()->initialise_dt(dt);
 
 // Set IC
 set_initial_condition();
 
 //Output initial condition
 doc_solution(doc_info);
 
 //Increment counter for solutions 
 doc_info.number()++;

Next we set up the number of timesteps to be performed. If the code is run in validation mode, indicated by a non-zero number of command line arguments, we only perform two timesteps.

 
 // Maximum time
 double t_max=4.0;
 
 // Number of steps
 unsigned nstep=unsigned(t_max/dt);
 
 // If validation run only do 2 timesteps
 if (CommandLineArgs::Argc>1)
  { 
   nstep=2; 
   cout << "Validation run -- only doing two timesteps." << std::endl;
  }

Finally, we loop over the timesteps, solve the equations at each time level and document the results.

 
 // Timestepping loop
 for (unsigned istep=0;istep<nstep;istep++)
  {
   //Take fixed timestep without spatial adaptivity
   unsteady_newton_solve(dt);
      
   //Output solution
   doc_solution(doc_info);
     
   //Increment counter for solutions 
   doc_info.number()++;
  }
 
 // Close trace file
 Trace_file.close();
 
} // end of unsteady run

Comments and Exercises

Default parameters for the linear wave equations

The linear wave equation does not contain any parameters, therefore the Problem constructor only passed the pointer to the pointer to the source function to the elements. Passing the pointer to the source function is optional – if no source function pointer is specified, the linear-wave elements will use the default , so that the unforced linear wave equation is solved. You should confirm this by commenting out the assignment of the source function pointer in the Problem constructor – the code should (and does!) still compute the correct results. This is because the travelling-wave solution (5) is in fact a solution of the unforced wave equation – the source function defined in the namespace TanhSolnForLinearWave implements .

The errors induced by an impulsive start

View the animation of the results obtained from the simulation that was started impulsively and explain how the differences to the exact solution arise.
Does the error induced by the impulsive start decay with time? Contrast this with the behaviour in the unsteady heat example.

The use of Neumann boundary conditions.

Neumann ("flux") boundary conditions for the linear wave equation can be applied by attaching elements of type LinearWaveFluxElement<BULK_LINEAR_WAVE_ELEMENT> to the boundary in exactly the same way as in the Poisson and unsteady heat examples. We will therefore not discuss this case in detail but simply refer to the listing of the (well-documented) driver code two_d_linear_wave_flux.cc

Source files for this tutorial

The source files for this tutorial are located in the directory: demo_drivers/linear_wave/two_d_linear_wave/
The driver code is: demo_drivers/linear_wave/two_d_linear_wave/two_d_linear_wave.cc

PDF file

A pdf version of this document is available.