This tutorial demonstrates the use of unstructured meshes in 3D fluid-structure interaction problems. We combine two single-physics problems, namely

for which we have already created unstructured 3D meshes, using Hang Si's open-source mesh generator tetgen .

The problem

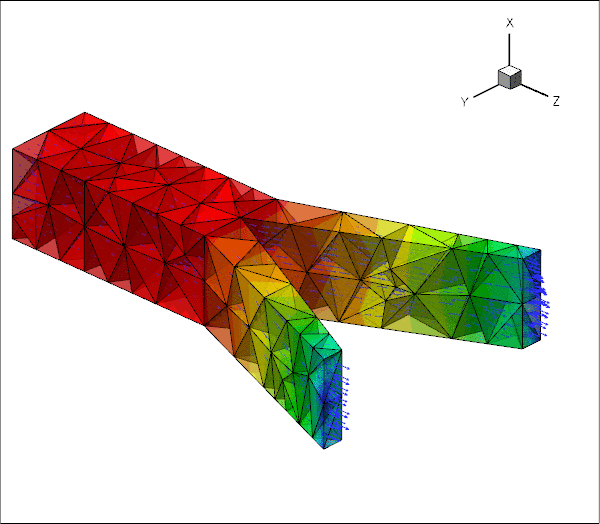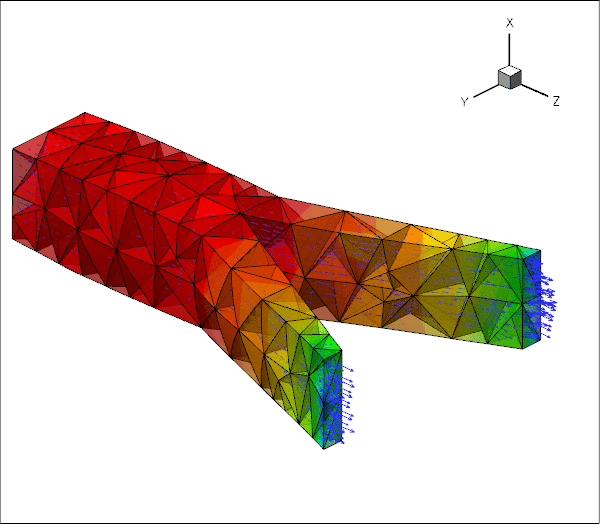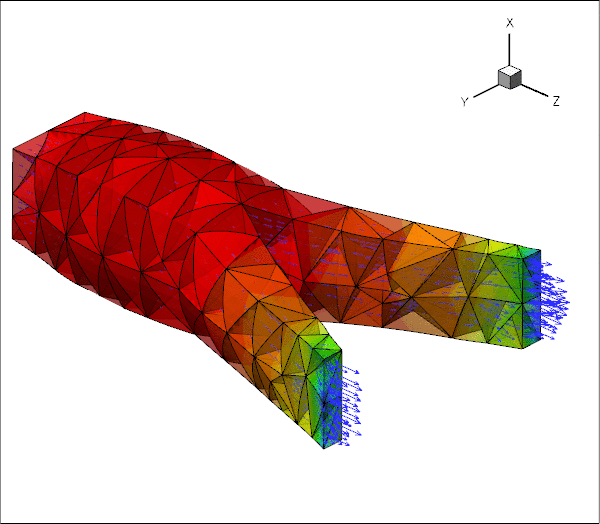
The two figures below show a sketch of the problem. An applied pressure drop drives fluid through an elastic, bifurcating tube whose branches have approximately rectangular cross-sections. We solve this problem as a fully-coupled fluid-structure interaction problem in which the fluid provides the traction onto the solid whose deformation changes the fluid domain.

Sketch of the problem.

Sketch of the problem (reverse view).

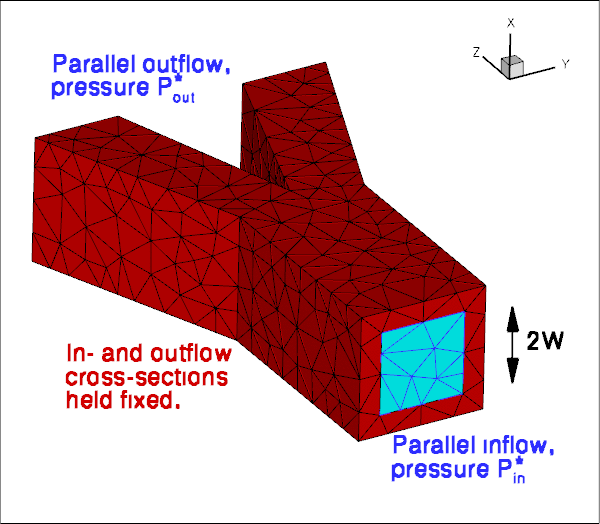
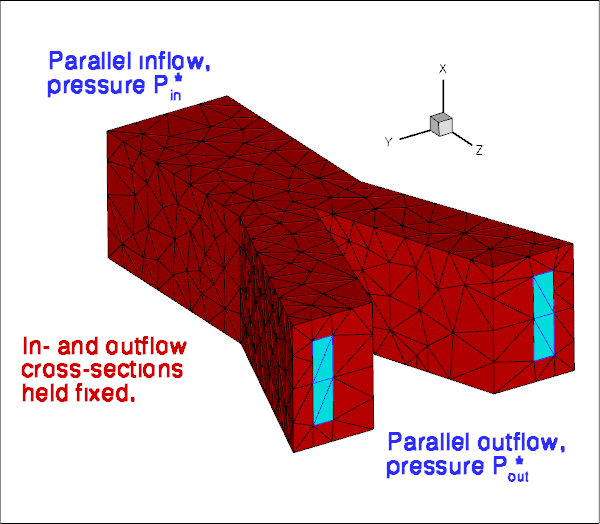
As usual, we formulate the problem in non-dimensional form. For this purpose we non-dimensionalise all lengths on the half-width, , of the square inflow cross-section, and use the overall pressure drop, $\Delta P^* = P_{in}^* - P_{out}^*$ to define the (viscous) velocity scale

${\cal U} = \frac{\Delta P^*\ W}{\mu}.$

With this choice the Reynolds number becomes

$Re = \frac{\rho {\cal U} W }{\mu} = \frac{ \Delta P^* \rho W^2 }{\mu^2},$

and we choose to drive the flow by a dimensionless pressure drop of $\Delta P = 1.$ Using this non-dimensionalisation an increase in the Reynolds number may be interpreted as in increase in the applied (dimensional) pressure drop along the vessel. Note that all pressures are defined relative to an external pressure, which we set to zero.

We assume that the solid's constitutive equation is given by oomph-lib's generalised Hookean constitutive law and non-dimensionalise the solid-mechanics stresses and tractions with the Young's modulus .

The FSI interaction parameter which represents the ratio of the (viscous) fluid stress scale to the reference stress used to non-dimensionalise the solid stresses, is therefore given by

$Q = \frac{\mu {\cal U}}{{\cal L} E} = \frac{\Delta P^*}{E} \ .$

Results

The animation below illustrates the system's behaviour in a parameter study in which we keep the Reynolds number fixed at while increasing the FSI parameter in small increments. The increase in may be interpreted as a reduction in the tube's stiffness and the animation shows clearly how this increases the flow-induced deformation: the upstream end bulges and the downstream end is compressed.

Animation of the flow field (pressure contours and velocity vectors).

Animation of the wall deformation -- the vectors indicate the fluid load.

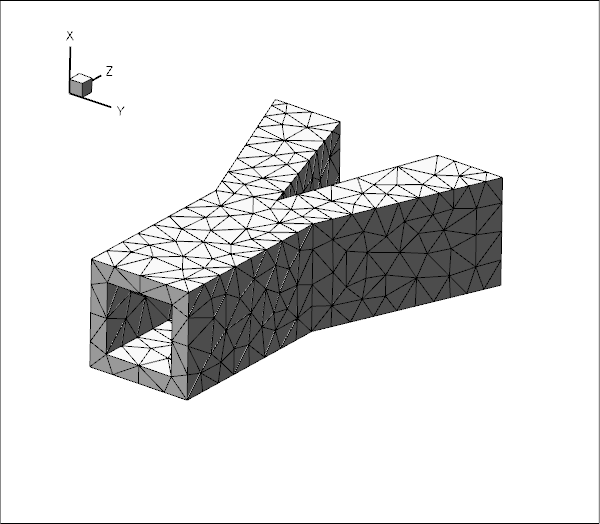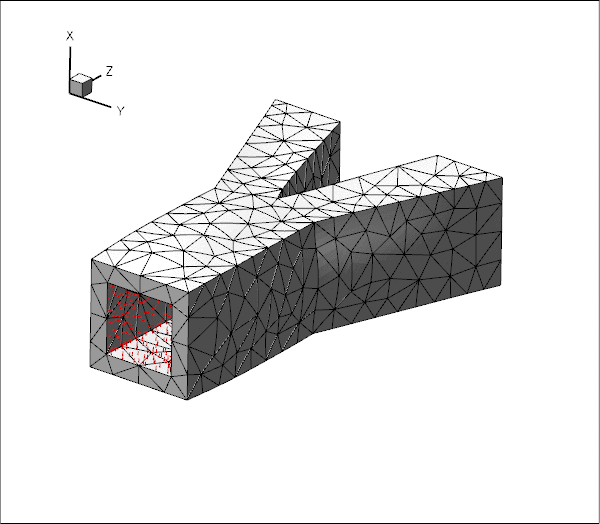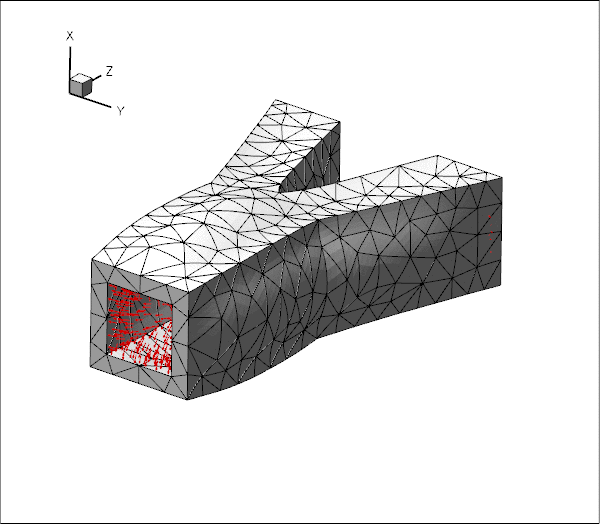
Overview of the implementation

The general procedure described below is essentially the same as that discussed in the two-dimensional unstructured FSI tutorial. The use of an unstructured mesh means that the most convenient node-update strategy for the fluid mesh is to treat it as a pseudo-elastic solid. Nonetheless, the majority of the steps described below are the same as for other fluid-structure-interaction problems.

We reiterate that an important prerequisite for the use of the automatic FSI_functions is that each boundary between fluid and solid meshes must be parametrised by boundary coordinates. Moreover, the boundary-coordinate representations must be the same in both the fluid and solid meshes. This use of a continuous-coordinate representation of the boundaries means that the fluid and solid meshes do not need to match at the boundaries; see the section Fluid and solid meshes do not have to be matching. Unfortunately, the construction of a global surface parametrisation of a general surface is a non-trivial problem. We side-step this problem by making use of the fact that any third-party tetrahedral mesh generator represents domain boundaries using a surface triangulation, or planar surface facets. As the mesh is imported into oomph-lib, each surface facet is treated as a separate boundary and given a unique boundary identifier. The surface parametrisation of each facet is then simply given by local coordinates of the plane; see How the boundary coordinates are generated. A consequence of this approach is that the physical boundaries will consist of several mesh "boundaries", as already discussed in the single-physics problems.

Since the driver code, discussed in detail below, is somewhat lengthy (partly because of the large number of self-tests and diagnostics included), we provide a brief overview of the main steps required to solve this problem:

Use the unstructured 3D mesh generator tetgen to generate the solid mesh, using the procedure discussed in another tutorial.
Use the same procedure to generate the fluid mesh, as discussed in the single-physics fluids tutorial. Make sure that the fluid mesh is derived from the SolidMesh base class to allow the use of pseudo-elasticity to update the nodal positions in response to the deformation of the domain boundary.
Ensure that boundary coordinates are set up (consistently) on the FSI interface between the two meshes. For meshes derived from oomph-lib's TetgenMesh class, this may be done by calling the function TetgenMesh::setup_boundary_coordinates(); see the section How the boundary coordinates are generated for details.
Attach FSISolidTractionElements to the faces of the "bulk" solid elements that are exposed to the fluid flow. These elements will apply the fluid traction to the solid.
Combine the FSISolidTractionElements to a compound GeomObject that provides a continuous representation of the solid's FSI boundary, required by the ImposeDisplacementByLagrangeMultiplierElements described below.
Attach ImposeDisplacementByLagrangeMultiplierElements to the faces of the "bulk" fluid elements that are adjacent to the solid. These elements will employ Lagrange multipliers to deform the pseudo-solid fluid mesh so that its shape remains consistent with the motion of the solid's FSI boundary (as described by the compound GeomObject created in the previous step).
Determine the "bulk" fluid elements that are adjacent to the integration points of the FSISolidTractionElements, using the function FSI_functions::setup_fluid_load_info_for_solid_elements(...).

In our experience, just as in two-dimensions, the most error-prone part of this procedure is the identification of the mesh boundaries. In particular, if the description of the FSI interface as viewed from the fluid and solid meshes is inconsistent, the automatic matching of the unstructured fluid and solid meshes will not work (see How the boundary coordinates are generated for details). For this reason, the driver code presented below generates a lot of output that can be used to identify and fix such problems. See also the section What can go wrong? at the end of this tutorial.

Problem Parameters

As usual we define the various problem parameters in a global namespace. We define the Reynolds number, , and the FSI interaction parameter .

//=======start_of_namespace==========================================
/// Global variables
//================================================================
namespace Global_Parameters
{
 
 /// Default Reynolds number
 double Re=100.0; 
 
 /// Default FSI parameter
 double Q=0.0;

We provide a pointer to the constitutive equation for the solid. For simplicity, the same constitutive equation will also be used for the (pseudo-)solid elements that determine the deformation of the fluid mesh. In general, of course, a different constitutive equation can (and probably should) be used to control the mesh motion.

 
 /// Pointer to constitutive law
 ConstitutiveLaw* Constitutive_law_pt=0;
 
 /// Poisson's ratio for generalised Hookean constitutive equation
 double Nu=0.3;

Finally, we define the tractions that act on the fluid at the in- and outflow cross-sections. We enforce the non-dimensional pressure drop of $\Delta P = 1$ (on the viscous scale) by setting $P_{in} = -P_{out}=0.5$ , thus pressurising the tube's upstream end while applying an equal and opposite "suction" downstream. (Note that in the
corresponding single-physics fluids problem the actual pressure values were irrelevant because the vessel walls were rigid. In the FSI problem considered here it obviously makes a big difference if the fluid pressure is positive or negative because the external reference pressure is set to zero.)

 
 /// Fluid pressure on inflow boundary
 double P_in=0.5;
 
 /// Applied traction on fluid at the inflow boundary
 void prescribed_inflow_traction(const double& t,
                                 const Vector<double>& x,
                                 const Vector<double>& n,
                                 Vector<double>& traction)
 {
  traction[0]=0.0;
  traction[1]=0.0;
  traction[2]=P_in;
 } 
 
 
 /// Fluid pressure on outflow boundary
 double P_out=-0.5; 
 
 /// Applied traction on fluid at the inflow boundary
 void prescribed_outflow_traction(const double& t,
                                  const Vector<double>& x,
                                  const Vector<double>& n,
                                  Vector<double>& traction)
 {
  traction[0]=0.0;
  traction[1]=0.0;
  traction[2]=-P_out;
 } 
 
 
} //end_of_namespace

Creating the meshes

The solid mesh

Following the procedure discussed in the single-physics solid mechanics problem we create the mesh for the elastic tube using multiple inheritance from oomph-lib's TetgenMesh and the SolidMesh base class.

//==========start_solid_mesh===============================================
/// Tetgen-based mesh upgraded to become a solid mesh
//=========================================================================
template<class ELEMENT>
class MySolidTetgenMesh : public virtual TetgenMesh<ELEMENT>, 
                       public virtual SolidMesh 
{

As before, we set the Lagrangian coordinates to the current nodal positions to make the initial configuration stress-free. Next, we identify the elements next to the various boundaries (recall that the domain boundaries are specified in the tetgen *.poly file), and set up the boundary coordinates. Adopting our usual state of continuous paranoia, we document these elements to facilitate debugging; see the section How the boundary coordinates are generated for details.

 
public:
 
 /// Constructor: 
 MySolidTetgenMesh(const std::string& node_file_name,
                const std::string& element_file_name,
                const std::string& face_file_name,
                TimeStepper* time_stepper_pt=
                &Mesh::Default_TimeStepper) : 
  TetgenMesh<ELEMENT>(node_file_name, element_file_name,
                      face_file_name, time_stepper_pt)
  {
   //Assign the Lagrangian coordinates
   set_lagrangian_nodal_coordinates();
 
   // Find elements next to boundaries
   setup_boundary_element_info();
 
   // Setup boundary coordinates for all boundaries
   char filename[100];
   ofstream some_file;
   unsigned nb=this->nboundary();
   for (unsigned b=0;b<nb;b++)
    {
     sprintf(filename,"RESLT/solid_boundary_test%i.dat",b);
     some_file.open(filename);
     this->template setup_boundary_coordinates<ELEMENT>(b,some_file);
     some_file.close();
    }
 
  }
 
 /// Empty Destructor
 virtual ~MySolidTetgenMesh() { }
 
};

The fluid mesh

The creation of the fluid mesh follows the same process but uses the mesh created for the
single-physics fluids problem. The use of multiple inheritance from the TetgenMesh and SolidMesh base classes is required to use pseudo-solid node-update techniques to move the fluid nodes in response to changes in the domain boundary. We refer to the fluids tutorial for a discussion of the split_corner_elements flag.

//==============start_fluid_mesh===========================================
/// Tetgen-based mesh upgraded to become a (pseudo-) solid mesh
//=========================================================================
template<class ELEMENT>
class FluidTetMesh : public virtual TetgenMesh<ELEMENT>,
                     public virtual SolidMesh 
{
 
public:
 
 /// Constructor: 
 FluidTetMesh(const std::string& node_file_name,
              const std::string& element_file_name,
              const std::string& face_file_name,
              const bool& split_corner_elements,
              TimeStepper* time_stepper_pt=
              &Mesh::Default_TimeStepper) : 
  TetgenMesh<ELEMENT>(node_file_name, element_file_name,
                      face_file_name, split_corner_elements, 
                      time_stepper_pt)
  {
   //Assign the Lagrangian coordinates
   set_lagrangian_nodal_coordinates();
 
   // Find out elements next to boundary
   setup_boundary_element_info();

We create boundary coordinates along all mesh boundaries. To ensure that fluid and solid boundary coordinates are aligned properly, we use the flag switch_normal to change the direction of the normal vector for the fluid mesh; see How the boundary coordinates are generated for details.

 
   // Setup boundary coordinates for boundary.
   // To be consistent with the boundary coordinates generated
   // in the solid, we switch the direction of the normal.
   // (Both meshes are generated from the same polygonal facets
   // at the FSI interface).
   bool switch_normal=true;
 
   // Setup boundary coordinates for all boundaries
   char filename[100];
   ofstream some_file;
   unsigned nb=this->nboundary();
   for (unsigned b=0;b<nb;b++) 
    {
     sprintf(filename,"RESLT/fluid_boundary_test%i.dat",b);
     some_file.open(filename);
     this->template setup_boundary_coordinates<ELEMENT>(b,switch_normal,some_file);
     some_file.close();
    }
 
  }
 
 /// Empty Destructor
 virtual ~FluidTetMesh() { }
 
};

The driver code

We specify an output directory and instantiate the constitutive equation (oomph-lib's generalisation of Hooke's law), specifying a Poisson ratio of 0.3. As discussed above, this constitutive equation will be used for the "proper" solid mechanics that determines the deformation of the elastic vessel walls, and for the pseudo-solid that determines the deformation of the fluid mesh.

//========================= start_of_main=================================
/// Demonstrate how to solve an unstructured 3D FSI problem
//========================================================================
int main(int argc, char **argv)
{
 // Label for output
 DocInfo doc_info;
 
 // Output directory
 doc_info.set_directory("RESLT");
 
 // Create generalised Hookean constitutive equations
 Global_Parameters::Constitutive_law_pt = 
  new GeneralisedHookean(&Global_Parameters::Nu);

We create the Problem object and output the initial guess for the solution.

 
 //Set up the problem
 UnstructuredFSIProblem<
 PseudoSolidNodeUpdateElement<TTaylorHoodElement<3>, TPVDElement<3,3> >,
  TPVDElement<3,3> > problem;
 
 //Output initial configuration
 problem.doc_solution(doc_info);
 doc_info.number()++;   

Finally, we perform a parameter study in which we compute the solution of the fully-coupled FSI problem for increasing values of the FSI parameter – physically, an increase in can be interpreted as a reduction in the stiffness of the tube walls while keeping the fluid properties and the driving pressure drop constant.

 
 // Parameter study
 unsigned nstep=2;
 
 // Increment in FSI parameter
 double q_increment=5.0e-2;
 
 for (unsigned istep=0;istep<nstep;istep++)
  {
   // Solve the problem
   problem.newton_solve();
   
   //Output solution
   problem.doc_solution(doc_info);
   doc_info.number()++;
 
   // Bump up FSI parameter
   Global_Parameters::Q+=q_increment;   
  }
 
} // end_of_main

The Problem class

The Problem class has the usual members, with access functions to the fluid and solid meshes, and a post-processing routine.

//===============start_of_problem_class===============================
/// Unstructured 3D FSI problem
//====================================================================
template<class FLUID_ELEMENT, class SOLID_ELEMENT>
class UnstructuredFSIProblem : public Problem
{
 
public:
 
 /// Constructor: 
 UnstructuredFSIProblem();
 
 /// Destructor (empty)
 ~UnstructuredFSIProblem(){}
 
 /// Doc the solution
 void doc_solution(DocInfo& doc_info);

We provide several helper functions to create the FaceElements that (i) apply the applied traction on the fluid at the in- and outflow cross-sections; (ii) apply the fluid traction onto the solid, and (iii) create the Lagrange multipliers that apply the solid displacement onto the pseudo-solid fluid mesh.

 
 /// Create fluid traction elements at inflow
 void create_fluid_traction_elements();
 
 /// Create FSI traction elements
 void create_fsi_traction_elements();
 
 /// Create elements that enforce prescribed boundary motion
 /// for the pseudo-solid fluid mesh by Lagrange multipliers
 void create_lagrange_multiplier_elements();

We also provide a helper function that documents the boundary coordinates on the solid mesh.

 
private:
 
 /// Sanity check: Doc boundary coordinates on i-th solid FSI interface
 void doc_solid_boundary_coordinates(const unsigned& i);

Finally we provide a large number of additional helper functions that specify the various mesh boundaries (as defined in the tetgen *.poly file) that make up the physical boundaries of interest: the in- and outflow boundaries in the fluid domain; the FSI boundaries of the fluid and solid domains and the boundaries along which the tube wall is held in a fixed position.

 
 /// Return total number of mesh boundaries that make up the inflow 
 /// boundary
 unsigned nfluid_inflow_traction_boundary()
  {return Inflow_boundary_id.size();}
 
 ///  Return total number of mesh boundaries that make up the outflow 
 /// boundary
 unsigned nfluid_outflow_traction_boundary()
  {return Outflow_boundary_id.size();}
 
 /// Return total number of mesh boundaries that make up the 
 /// in- and outflow boundaries where a traction has to be applied
 unsigned nfluid_traction_boundary()
  {return Inflow_boundary_id.size()+Outflow_boundary_id.size();}
 
 /// Return total number of mesh boundaries in the solid mesh that
 /// make up the FSI interface
 unsigned nsolid_fsi_boundary()
  {return Solid_fsi_boundary_id.size();}
 
 /// Return total number of mesh boundaries in the fluid mesh that
 /// make up the FSI interface
 unsigned nfluid_fsi_boundary()
  {return Fluid_fsi_boundary_id.size();}
 
 /// Return total number of mesh boundaries in the solid mesh 
 /// where the position is pinned.
 unsigned npinned_solid_boundary()
  {return Pinned_solid_boundary_id.size();} 
  //end npinned_solid_boundary

The private member data includes pointers to the various meshes and the GeomObject representation of the FSI boundary (created from the FaceElements attached to the solid mesh).

 
 
 /// Bulk solid mesh
 MySolidTetgenMesh<SOLID_ELEMENT>* Solid_mesh_pt;
 
 /// Meshes of FSI traction elements
 Vector<SolidMesh*> Solid_fsi_traction_mesh_pt;
 
 /// Bulk fluid mesh
 FluidTetMesh<FLUID_ELEMENT>* Fluid_mesh_pt;
 
 /// Meshes of fluid traction elements that apply pressure at in/outflow
 Vector<Mesh*> Fluid_traction_mesh_pt;
 
 /// Meshes of Lagrange multiplier elements
 Vector<SolidMesh*> Lagrange_multiplier_mesh_pt;
 
 /// GeomObject incarnations of the FSI boundary in the solid mesh
 Vector<MeshAsGeomObject*>
 Solid_fsi_boundary_pt;

Finally, here are the vectors that store the mesh boundary IDs associated with the various domain boundaries of interest.

 
 /// IDs of solid mesh boundaries where displacements are pinned
 Vector<unsigned> Pinned_solid_boundary_id;
  
 /// IDs of solid mesh boundaries which make up the FSI interface
 Vector<unsigned> Solid_fsi_boundary_id;
 
 /// IDs of fluid mesh boundaries along which inflow boundary conditions
 /// are applied
 Vector<unsigned> Inflow_boundary_id;
 
 /// IDs of fluid mesh boundaries along which inflow boundary conditions
 /// are applied
 Vector<unsigned> Outflow_boundary_id;
 
 /// IDs of fluid mesh boundaries which make up the FSI interface
 Vector<unsigned> Fluid_fsi_boundary_id;
 
};

The Problem constructor

We start by building the fluid mesh, using the files created by tetgen ; see the discussion in the corresponding single-physics fluids problem.

//==========start_of_constructor==========================================
/// Constructor for unstructured 3D FSI problem
//========================================================================
template<class FLUID_ELEMENT, class SOLID_ELEMENT>
UnstructuredFSIProblem<FLUID_ELEMENT,SOLID_ELEMENT>::UnstructuredFSIProblem()
{ 
 // Define fluid mesh and its distinguished boundaries
 //---------------------------------------------------
 
   //Create fluid bulk mesh, sub-dividing "corner" elements
 string node_file_name="fsi_bifurcation_fluid.1.node";
 string element_file_name="fsi_bifurcation_fluid.1.ele";
 string face_file_name="fsi_bifurcation_fluid.1.face";
 bool split_corner_elements=true;
 Fluid_mesh_pt =  new FluidTetMesh<FLUID_ELEMENT>(node_file_name,
                                                  element_file_name,
                                                  face_file_name,
                                                  split_corner_elements);

Next we associated the tetgen boundary IDs with the various boundaries of interest: The inflow boundary is represented by tetgen boundary 0, and the two outflow boundaries have IDs 1 and 2.

 
 
 // The following corresponds to the boundaries as specified by
 // facets in the tetgen input:
 
 // Fluid mesh has one inflow boundary: Boundary 0
 Inflow_boundary_id.resize(1);
 Inflow_boundary_id[0]=0;
 
 // Fluid mesh has two outflow boundaries: Boundaries 1 and 2
 Outflow_boundary_id.resize(2);
 Outflow_boundary_id[0]=1;
 Outflow_boundary_id[1]=2;

The FSI boundary (i.e. the boundary of the fluid mesh that is exposed to the elastic vessel wall) comprises 12 separate tetgen facets which were numbered 3 to 14 in the *.poly that describes the fluid mesh.

 
 // The remaining fluid boundaries are FSI boundaries.
 // Note that their order (as indexed in this vector, not
 // their actual numbers) have to match those in the corresponding
 // lookup scheme for the solid.
 Fluid_fsi_boundary_id.resize(12);
 for (unsigned i=0;i<12;i++)
  {
   Fluid_fsi_boundary_id[i]=i+3;
  }

Next, we create the solid mesh, using the files created by tetgen ; see the discussion in the corresponding single-physics solids problem.

 // Define solid mesh and its distinguished boundaries
 //---------------------------------------------------
 
 //Create solid bulk mesh
 node_file_name="fsi_bifurcation_solid.1.node";
 element_file_name="fsi_bifurcation_solid.1.ele";
 face_file_name="fsi_bifurcation_solid.1.face";
 Solid_mesh_pt =  new MySolidTetgenMesh<SOLID_ELEMENT>(node_file_name,
                                                    element_file_name,
                                                    face_file_name);

Following the procedure used for the fluid mesh, we identify the mesh boundaries that make up the (pinned) ends of the tube (boundaries 0, 1 and 2, as defined in the tetgen *.poly file) and the FSI boundary (boundaries 3 to 14 – note that this enumeration matches that in the fluid mesh; see How the boundary coordinates are generated for further details of how the fluid and solid meshes are matched).

 
 // The following corresponds to the boundaries as specified by
 // facets in the tetgen input:
 
 /// IDs of solid mesh boundaries where displacements are pinned
 Pinned_solid_boundary_id.resize(3);
 Pinned_solid_boundary_id[0]=0;
 Pinned_solid_boundary_id[1]=1;
 Pinned_solid_boundary_id[2]=2;
 
 // The solid and fluid fsi boundaries are numbered int he same way.
 Solid_fsi_boundary_id.resize(12);
 for (unsigned i=0;i<12;i++)
  {
   Solid_fsi_boundary_id[i]=i+3;
  }

We create the fluid traction elements that impose the applied pressures in the in- and outflow cross-sections.

 
 
 
 // Create (empty) meshes of fluid traction elements at inflow/outflow
 //-----------------------------------------------------------
 
 // Create the meshes
 unsigned n=nfluid_traction_boundary();
 Fluid_traction_mesh_pt.resize(n);
 for (unsigned i=0;i<n;i++)
  {
   Fluid_traction_mesh_pt[i]=new Mesh;
  } 
 
 // Populate them with elements
 create_fluid_traction_elements();

Next, we create the FaceElements that apply the fluid traction to the solid,

 
 
// Create FSI Traction elements
//-----------------------------
 
// Create (empty) meshes of FSI traction elements
 n=nsolid_fsi_boundary();
 Solid_fsi_traction_mesh_pt.resize(n);
 for (unsigned i=0;i<n;i++)
  {
   Solid_fsi_traction_mesh_pt[i]=new SolidMesh;
  }
 
 // Build the FSI traction elements
 create_fsi_traction_elements();

and the FaceElements that use Lagrange multipliers to deform the fluid mesh to keep it aligned with the FSI boundary.

 
 
 // Create Lagrange multiplier mesh for boundary motion of fluid mesh
 //------------------------------------------------------------------
  
 // Construct the mesh of elements that enforce prescribed boundary motion
 // of pseudo-solid fluid mesh by Lagrange multipliers
 n=nfluid_fsi_boundary();
 Lagrange_multiplier_mesh_pt.resize(n);
 for (unsigned i=0;i<n;i++)
  {
   Lagrange_multiplier_mesh_pt[i]=new SolidMesh;
  }
 
 // Create elements
 create_lagrange_multiplier_elements();

We combine the various sub-meshes to a global mesh.

 
 
 // Combine the lot
 //----------------
 
 // Add sub meshes:
 
 // The solid bulk mesh
 add_sub_mesh(Solid_mesh_pt);
 
 // Fluid bulk mesh
 add_sub_mesh(Fluid_mesh_pt);
 
 // The fluid traction meshes
 n=nfluid_traction_boundary();
 for (unsigned i=0;i<n;i++)
  { 
   add_sub_mesh(Fluid_traction_mesh_pt[i]);
  }
 
 // The solid fsi traction meshes
 n=nsolid_fsi_boundary();
 for (unsigned i=0;i<n;i++)
  {
   add_sub_mesh(Solid_fsi_traction_mesh_pt[i]);
  }
 
 // The Lagrange multiplier meshes for the fluid
 n=nfluid_fsi_boundary();
 for (unsigned i=0;i<n;i++)
  {   
   add_sub_mesh(Lagrange_multiplier_mesh_pt[i]);
  }
 
 // Build global mesh
 build_global_mesh();

Next, we apply the boundary conditions for the fluid mesh: We impose parallel in- and outflow at the in- and outflow boundaries and apply boundary conditions for the pseudo-elastic deformation of the fluid mesh. Since the in- and outflow cross-sections of the elastic tube are held in place, we pin the position of the fluid nodes in these cross-sections too. To facilitate debugging we document the position of the fluid nodes whose (pseudo-solid) displacements we suppressed.

 
 
 
 
 // Apply BCs for fluid
 //--------------------
  
 // Doc position of pinned pseudo solid nodes
 std::ofstream pseudo_solid_bc_file("RESLT/pinned_pseudo_solid_nodes.dat");
 
 // Loop over inflow/outflow boundaries to impose parallel flow
 // and pin pseudo-solid displacements
 for (unsigned in_out=0;in_out<2;in_out++)
  {
   // Loop over in/outflow boundaries
   unsigned n=nfluid_inflow_traction_boundary();
   if (in_out==1) n=nfluid_outflow_traction_boundary();
   for (unsigned i=0;i<n;i++)
    {
 
     // Get boundary ID
     unsigned b=0;
     if (in_out==0)
      {
       b=Inflow_boundary_id[i];
      }
     else
      {
       b=Outflow_boundary_id[i];
      }
 
     // Number of nodes on that boundary
     unsigned num_nod=Fluid_mesh_pt->nboundary_node(b);
     for (unsigned inod=0;inod<num_nod;inod++)
      {
       // Get the node
       SolidNode* nod_pt=Fluid_mesh_pt->boundary_node_pt(b,inod);
       
       // Pin transverse velocities
       nod_pt->pin(0);
       nod_pt->pin(1);
       
       // Pin the nodal (pseudo-solid) displacements
       for(unsigned i=0;i<3;i++)
        {         
         nod_pt->pin_position(i);         
         
         // Doc it as pinned
         pseudo_solid_bc_file << nod_pt->x(i) << " ";
        }
      }
    }
  }
 
 // Close
 pseudo_solid_bc_file.close();

We apply the no-slip condition on the fluid nodes that are located on the FSI boundary. In addition, we apply boundary conditions for the Lagrange multipliers. We pin the Lagrange multipliers for nodes that are located on the in- and outflow boundaries where the nodal positions are pinned. Recall that the Lagrange multipliers are additional degrees of freedom that are added to the "bulk" degrees of freedom that were originally created by the "bulk" element. The storage for the Lagrange multipliers is added to the Nodes by the FaceElements and the values at which the Lagrange multipliers are stored are found using the function BoundaryNodeBase::index_of_first_value_assigned_by_face_element(). The documentation of the position of the pinned Lagrange multiplier nodes in RESLT/pinned_lagrange_multiplier_nodes.dat is here to facilitate the debugging of the code and is highly recommended.

 
 // Doc bcs for Lagrange multipliers
 ofstream pinned_file("RESLT/pinned_lagrange_multiplier_nodes.dat");
 
 // Loop over all fluid mesh boundaries and pin velocities
 // of nodes that haven't been dealt with yet
 unsigned nbound=nfluid_fsi_boundary();
 for(unsigned i=0;i<nbound;i++)
  {
   //Get the mesh boundary
   unsigned b = Fluid_fsi_boundary_id[i];
   
   unsigned num_nod=Fluid_mesh_pt->nboundary_node(b);
   for (unsigned inod=0;inod<num_nod;inod++)
    {
     // Get node
     Node* nod_pt= Fluid_mesh_pt->boundary_node_pt(b,inod);
     
     // Pin all velocities
     nod_pt->pin(0); 
     nod_pt->pin(1); 
     nod_pt->pin(2); 
     
     // Find out whether node is also on in/outflow
     bool is_in_or_outflow_node=false;
     unsigned n=nfluid_inflow_traction_boundary();
     for (unsigned k=0;k<n;k++)
      {
       if (nod_pt->is_on_boundary(Inflow_boundary_id[k]))
        {
         is_in_or_outflow_node=true;
         break;
        }
      }
     if (!is_in_or_outflow_node)
      {
       unsigned n=nfluid_outflow_traction_boundary();
       for (unsigned k=0;k<n;k++)
        {
         if (nod_pt->is_on_boundary(Outflow_boundary_id[k]))
          {
           is_in_or_outflow_node=true;
           break;
          }
        }
      }
 
     // Pin the Lagrange multipliers on the out/in-flow boundaries
     if (is_in_or_outflow_node)
      {
       //Cast to a boundary node
       BoundaryNode<SolidNode> *bnod_pt = 
        dynamic_cast<BoundaryNode<SolidNode>*>
        ( Fluid_mesh_pt->boundary_node_pt(b,inod) );
              
       // Loop over the Lagrange multipliers
       for (unsigned l=0;l<3;l++)
        {
         // Pin the Lagrange multipliers that impose the displacement
         // because the positon of the fluid nodes at the in/outflow
         // is already determined. 
         nod_pt->pin
          (bnod_pt->index_of_first_value_assigned_by_face_element()+l);
        }
 
       // Doc that we've pinned the Lagrange multipliers at this node
       pinned_file << nod_pt->x(0) << " "
                   << nod_pt->x(1) << " "
                   << nod_pt->x(2) << endl;
      }
    }
   
  } // done no slip on fsi boundary
 
 // Done
 pinned_file.close();

We complete the build of the fluid elements by specifying the Reynolds number and the constitutive equation for the pseudo-solid equations; recall that we use the same constitutive equation as used for the tube wall.

 
 // Complete the build of the fluid elements so they are fully functional
 //----------------------------------------------------------------------
 unsigned n_element = Fluid_mesh_pt->nelement();
 for(unsigned e=0;e<n_element;e++)
  {
   // Upcast from GeneralisedElement to the present element
   FLUID_ELEMENT* el_pt = 
    dynamic_cast<FLUID_ELEMENT*>(Fluid_mesh_pt->element_pt(e));
   
   //Set the Reynolds number
   el_pt->re_pt() = &Global_Parameters::Re;
   
   // Set the constitutive law for pseudo-elastic mesh deformation
   el_pt->constitutive_law_pt() =
    Global_Parameters::Constitutive_law_pt;
   
  } // end loop over elements

We apply the "solid" boundary conditions by pinning the positions of the nodes that are located at the ends of the elastic tube, and, just to be on the safe side, document their positions to allow for debugging and sanity-checking.

 
 
 
 // Apply BCs for solid
 //--------------------
 
 // Doc pinned solid nodes
 std::ofstream bc_file("RESLT/pinned_solid_nodes.dat");
 
 // Pin positions at inflow boundary (boundaries 0 and 1)
 n=npinned_solid_boundary();
 for (unsigned i=0;i<n;i++)
  {
   // Get boundary ID
   unsigned b=Pinned_solid_boundary_id[i];
   unsigned num_nod= Solid_mesh_pt->nboundary_node(b);  
   for (unsigned inod=0;inod<num_nod;inod++)
    {    
     // Get node
     SolidNode* nod_pt=Solid_mesh_pt->boundary_node_pt(b,inod);
     
     // Pin all directions
     for (unsigned i=0;i<3;i++)
      {
       nod_pt->pin_position(i);
       
       // ...and doc it as pinned
       bc_file << nod_pt->x(i) << " ";
      }
     
     bc_file << std::endl;
    }
  }
 bc_file.close();

We complete the build of the solid elements by passing the pointer to the constitutive equation.

 
 
 
 // Complete the build of Solid elements so they are fully functional
 //----------------------------------------------------------------
 n_element = Solid_mesh_pt->nelement();
 for(unsigned i=0;i<n_element;i++)
  {
   //Cast to a solid element
   SOLID_ELEMENT *el_pt = dynamic_cast<SOLID_ELEMENT*>(
    Solid_mesh_pt->element_pt(i));
   
   // Set the constitutive law   
   el_pt->constitutive_law_pt() =
    Global_Parameters::Constitutive_law_pt;
  }

Finally, we set up the fluid-structure interaction by determining which "bulk" fluid elements are located next to the FSI traction elements that apply the fluid load to the solid. This must be done separately for each of the mesh boundaries that make up the physical FSI boundary. To facilitate debugging, we document the boundary coordinates along the FSI interface (as seen by the fluid) by opening the Multi_domain_functions::Doc_boundary_coordinate_file stream before calling FSI_functions::setup_fluid_load_info_for_solid_elements(...). If this stream is open, the setup routine writes the Eulerian coordinates of the points on the FSI interface and their intrinsic surface coordinate $[ x, y, z, \zeta_1, \zeta_2 ]$ to the specified file. This may be compared against the corresponding data for the solid's view of the FSI interface, documented in doc_solid_boundary_coordinates().

 
 
 // Setup FSI
 //----------
     
 // Work out which fluid dofs affect the residuals of the wall elements:
 // We pass the boundary between the fluid and solid meshes and 
 // pointers to the meshes. 
 n=nsolid_fsi_boundary();
 for (unsigned i=0;i<n;i++)
  {
   // Sanity check: Doc boundary coordinates from solid side
   doc_solid_boundary_coordinates(i);
   
   //Doc boundary coordinates in fluid
   char filename[100];
   sprintf(filename,"RESLT/fluid_boundary_coordinates%i.dat",i);
   Multi_domain_functions::Doc_boundary_coordinate_file.open(filename);
   
   // Setup FSI: Pass ID of fluid FSI boundary and associated
   // mesh of solid fsi traction elements.
   FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,3>
    (this,Fluid_fsi_boundary_id[i],Fluid_mesh_pt,Solid_fsi_traction_mesh_pt[i]);
   
   // Close the doc file
   Multi_domain_functions::Doc_boundary_coordinate_file.close();
  } 

All that's now left to do is to set up the equation numbering scheme and the problem is ready to be solved.

 
 // Setup equation numbering scheme
 std::cout <<"Number of equations: " << assign_eqn_numbers() << std::endl; 
 
}

Creating the FSI traction elements

The creation of the FSI traction elements that apply the fluid traction to the solid elements that are adjacent to the FSI boundary follows the usual procedure: We loop over the relevant 3D "bulk" solid elements and attach the FSISolidTractionElements to the appropriate faces.

//============start_of_create_fsi_traction_elements======================
/// Create FSI traction elements 
//=======================================================================
template<class FLUID_ELEMENT,class SOLID_ELEMENT>
void UnstructuredFSIProblem<FLUID_ELEMENT,SOLID_ELEMENT>::
create_fsi_traction_elements()
{
 
 // Loop over FSI boundaries in solid
 unsigned n=nsolid_fsi_boundary();
 for (unsigned i=0;i<n;i++)
  {
   // Get boundary ID
   unsigned b=Solid_fsi_boundary_id[i];
   
   // How many bulk elements are adjacent to boundary b?
   unsigned n_element = Solid_mesh_pt->nboundary_element(b);
   
   // Loop over the bulk elements adjacent to boundary b
   for(unsigned e=0;e<n_element;e++)
    {
     // Get pointer to the bulk element that is adjacent to boundary b
     SOLID_ELEMENT* bulk_elem_pt = dynamic_cast<SOLID_ELEMENT*>(
      Solid_mesh_pt->boundary_element_pt(b,e));
     
     //What is the index of the face of the element e along boundary b
     int face_index = Solid_mesh_pt->face_index_at_boundary(b,e);
     
     // Create new element 
     FSISolidTractionElement<SOLID_ELEMENT,3>* el_pt=
      new FSISolidTractionElement<SOLID_ELEMENT,3>(bulk_elem_pt,face_index);

Next we add the newly-created FaceElement to the mesh of traction elements, specify which boundary of the bulk mesh it is attached to, and pass the FSI interaction parameter to the element.

     
     // Add it to the mesh
     Solid_fsi_traction_mesh_pt[i]->add_element_pt(el_pt);
     
     // Specify boundary number
     el_pt->set_boundary_number_in_bulk_mesh(b);
     
     // Function that specifies the load ratios
     el_pt->q_pt() = &Global_Parameters::Q; 
    }
  }
 
} // end of create_fsi_traction_elements

Creating the Lagrange multiplier elements

The creation of the FaceElements that use Lagrange multipliers to impose the boundary displacement of the pseudo-solid fluid mesh is again fairly straightforward (the use of Lagrange multipliers for the imposition of boundary displacements is explained in another tutorial). The only complication is that we must loop over the different parts of the FSI boundary. In each case we combine the FSISolidTractionElements attached to the solid mesh into a compound GeomObject. Each GeomObject provides a continuous representation of the relevant part of the FSI boundary, parametrised by the boundary coordinate assigned earlier while its shape is determined by the deformation of the 3D solid elements that the FSISolidTractionElements are attached to.

 
 
//============start_of_create_lagrange_multiplier_elements===============
/// Create elements that impose the prescribed boundary displacement
/// for the pseudo-solid fluid mesh
//=======================================================================
template<class FLUID_ELEMENT, class SOLID_ELEMENT>
void UnstructuredFSIProblem<FLUID_ELEMENT,SOLID_ELEMENT>::
create_lagrange_multiplier_elements()
{
 // Make space
 unsigned n=nfluid_fsi_boundary();
 Solid_fsi_boundary_pt.resize(n);
    
 // Loop over FSI interfaces in fluid
 for (unsigned i=0;i<n;i++)
  {   
   // Get boundary ID
   unsigned b=Fluid_fsi_boundary_id[i];
   
   // Create  GeomObject incarnation of fsi boundary in solid mesh
   Solid_fsi_boundary_pt[i]=
    new MeshAsGeomObject
    (Solid_fsi_traction_mesh_pt[i]);

Having represented the boundary by a (compound) GeomObject, we now attach ImposeDisplacementByLagrangeMultiplierElements to the appropriate faces of the "bulk" fluid elements that are adjacent to the FSI interface and add them to their own mesh:

   
   // How many bulk fluid elements are adjacent to boundary b?
   unsigned n_element = Fluid_mesh_pt->nboundary_element(b);
   
   // Loop over the bulk fluid elements adjacent to boundary b?
   for(unsigned e=0;e<n_element;e++)
    {
     // Get pointer to the bulk fluid element that is adjacent to boundary b
     FLUID_ELEMENT* bulk_elem_pt = dynamic_cast<FLUID_ELEMENT*>(
      Fluid_mesh_pt->boundary_element_pt(b,e));
     
     //Find the index of the face of element e along boundary b
     int face_index = Fluid_mesh_pt->face_index_at_boundary(b,e);
     
     // Create new element
     ImposeDisplacementByLagrangeMultiplierElement<FLUID_ELEMENT>* el_pt =
      new ImposeDisplacementByLagrangeMultiplierElement<FLUID_ELEMENT>(
       bulk_elem_pt,face_index);   
     
     // Add it to the mesh
     Lagrange_multiplier_mesh_pt[i]->add_element_pt(el_pt);

Finally, we pass a pointer to the compound GeomObject that defines the shape of the FSI interface and specify which boundary in the "bulk" fluid mesh the ImposeDisplacementByLagrangeMultiplierElement is attached to.

     
     // Set the GeomObject that defines the boundary shape and set
     // which bulk boundary we are attached to (needed to extract
     // the boundary coordinate from the bulk nodes)
     el_pt->set_boundary_shape_geom_object_pt(Solid_fsi_boundary_pt[i],b);
    }
  }
 
} // end of create_lagrange_multiplier_elements

Attaching the fluid traction elements

The helper function create_fluid_traction_elements() attaches NavierStokesTractionElements to the in- and outflow cross-sections of the fluid mesh and thus imposes the prescribed pressure drop onto the fluid.

//============start_of_fluid_traction_elements==============================
/// Create fluid traction elements 
//=======================================================================
template<class FLUID_ELEMENT,class SOLID_ELEMENT>
void UnstructuredFSIProblem<FLUID_ELEMENT,SOLID_ELEMENT>::
create_fluid_traction_elements()
{
 
 // Counter for number of fluid traction meshes
 unsigned count=0;
 
 // Loop over inflow/outflow boundaries
 for (unsigned in_out=0;in_out<2;in_out++)
  {
   // Loop over boundaries with fluid traction elements
   unsigned n=nfluid_inflow_traction_boundary();
   if (in_out==1) n=nfluid_outflow_traction_boundary();
   for (unsigned i=0;i<n;i++)
    {
     
     // Get boundary ID
     unsigned b=0;
     if (in_out==0)
      {
       b=Inflow_boundary_id[i];
      }
     else
      {
       b=Outflow_boundary_id[i];
      }
 
     // How many bulk elements are adjacent to boundary b?
     unsigned n_element = Fluid_mesh_pt->nboundary_element(b);
     
     // Loop over the bulk elements adjacent to boundary b
     for(unsigned e=0;e<n_element;e++)
      {
       // Get pointer to the bulk element that is adjacent to boundary b
       FLUID_ELEMENT* bulk_elem_pt = dynamic_cast<FLUID_ELEMENT*>(
        Fluid_mesh_pt->boundary_element_pt(b,e));
       
       //What is the index of the face of the element e along boundary b
       int face_index = Fluid_mesh_pt->face_index_at_boundary(b,e);
       
       // Create new element 
       NavierStokesTractionElement<FLUID_ELEMENT>* el_pt=
        new NavierStokesTractionElement<FLUID_ELEMENT>(bulk_elem_pt,
                                                       face_index);
       
       // Add it to the mesh
       Fluid_traction_mesh_pt[count]->add_element_pt(el_pt);
         
       // Set the pointer to the prescribed traction function
       if (in_out==0)
        {
         el_pt->traction_fct_pt() = 
          &Global_Parameters::prescribed_inflow_traction;
        }
       else
        { 
         el_pt->traction_fct_pt() = 
          &Global_Parameters::prescribed_outflow_traction;
        }
      }
     // Bump up counter
     count++;
    }
  }
 
 } // end of create_traction_elements

Post-processing

The post-processing routine simply executes the output functions for the fluid and solid meshes and documents their mesh boundaries. We also document the FSI traction that the fluid exerts onto the solid.

//========start_of_doc_solution===========================================
/// Doc the solution
//========================================================================
template<class FLUID_ELEMENT, class SOLID_ELEMENT>
void UnstructuredFSIProblem<FLUID_ELEMENT,SOLID_ELEMENT>::
doc_solution(DocInfo& doc_info)
{ 
 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned npts;
 npts=5;
 
 // Output solid boundaries
 //------------------------
 sprintf(filename,"%s/solid_boundaries%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Solid_mesh_pt->output_boundaries(some_file);
 some_file.close();
 
 
 // Output solid solution
 //-----------------------
 sprintf(filename,"%s/solid_soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Solid_mesh_pt->output(some_file,npts);
 some_file.close();
 
 
 // Output fluid boundaries
 //------------------------
 sprintf(filename,"%s/fluid_boundaries%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Fluid_mesh_pt->output_boundaries(some_file);
 some_file.close();
 
 
 // Output fluid solution
 //-----------------------
 sprintf(filename,"%s/fluid_soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Fluid_mesh_pt->output(some_file,npts);
 some_file.close();
  
   
 // Output fsi traction
 //--------------------
 sprintf(filename,"%s/fsi_traction%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 unsigned n=nsolid_fsi_boundary();
 for (unsigned i=0;i<n;i++)
  {
   Solid_fsi_traction_mesh_pt[i]->output(some_file,npts);
  }
 some_file.close();
 
} // end_of_doc

Sanity check: Documenting the solid boundary coordinates

The function doc_solid_boundary_coordinates() documents the parametrisation of the solid's FSI boundary by writing into a file the solid's counterpart of the $[ x, y, z, \zeta_1, \zeta_2 ]$ data that we created for the fluid side of the FSI interface when setting up the fluid-structure interaction with FSI_functions::setup_fluid_load_info_for_solid_elements(...). The two parametrisations should be consistent; see What can go wrong? for more details. The implementation is straightforward and is suppressed for brevity; see the source code if you want to know how it works.

Comments and Exercises

How the boundary coordinates are generated

The use of pseudo-elasticity for the node update in the fluid mesh makes the solution of FSI problems extremely straightforward. They key feature that allows the "automatic" coupling of the unstructured fluid and solid meshes is the (consistent!) generation of the boundary coordinates $(\zeta_1,\zeta_2)$ along the FSI interface. For reasons already mentioned, the procedure is more involved than in the equivalent two-dimensional problem. The implementation of this functionality in TetgenMesh::setup_boundary_coordinates(...) exploits the fact that

Meshes generated by tetgen are bounded by planar facets, and
We insist that all facets are given distinct boundary IDs
when defining the domain in the tetgen *.poly file.

The figure below illustrates the generation of the boundary coordinates within a representative planar facet (shown in cyan) that defines a particular mesh boundary.

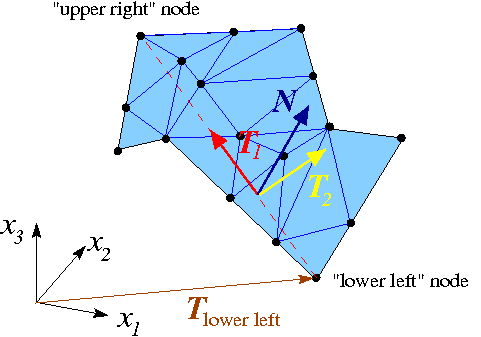
Sketch illustrating the generation of boundary coordinates on a mesh boundary that is defined by a planar facet (shown in cyan).

Here is how we generate the boundary coordinates:

We start by attaching FaceElements to the appropriate faces of the "bulk" elements that are adjacent to the mesh boundary defined by the facet. These FaceElements provide a surface triangulation of the boundary. In the sketch above, the surface triangulation is represented by the blue surface mesh.
We locate the "lower left" and "upper right" nodes within the surface mesh, based on a lexicographical ordering of the nodes' 3D coordinates.
The straight line from the "lower left" to the "upper right" node (shown by the dashed red line) defines a direction that is co-planar with the facet and therefore allows us to define an in-plane unit vector, 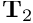${\bf T}_1$ , shown in red.
A second in-plane unit vector, 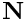${\bf T}_2$ (shown in yellow), can then be constructed by taking the cross-product of 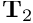${\bf T}_1$ and the outer unit normal 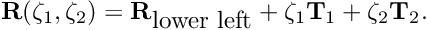${\bf N}$ . (The outer unit normal can be obtained from any of the adjacent bulk elements.)
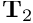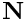The orthonormal in-plane vectors ${\bf T}_1$ and ${\bf T}_2$ define a unique parametrisation of the boundary in terms of the boundary coordinates 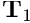$(\zeta_1,\zeta_2)$ , if we insist that for every point on the boundary we have
${\bf R}(\zeta_1,\zeta_2) = {\bf R}_{\mbox{lower left}} + \zeta_1 {\bf T}_1 + \zeta_2 {\bf T}_2.$
This allows the assignment of boundary coordinates for each of the nodes on this boundary.
Once this is done we can delete the FaceElements that defined the surface triangulation.

Since the generation of the boundary coordinates by the above procedure only relies on the position of the "lower left" and "upper right" vertices (which are properties of the facet rather than the tetgen mesh) the boundary coordinates are unique, regardless of the actual discretisation generated by tetgen. Furthermore, the boundary coordinates created from the fluid and solid meshes will be consistent provided we reverse the direction of the outer unit normal in one of the meshes. This is exactly what the switch_normal flag in TetgenMesh::setup_boundary_coordinates(...) is for. When generating the boundary coordinates for our problem, we switched the direction of the normal in the fluid mesh; see the section The fluid mesh, above.

Here is an animation of the automatically-generated boundary coordinates along the 12 mesh boundaries that constitute the FSI boundary, when viewed from the fluid and the solid, respectively. In each of the frames the contours indicate the value of
$\zeta_1$ within the respective boundary. Note that the boundary coordinates established in the two meshes match, even though the discretisations do not.

Contour plot of the automatically-generated boundary coordinates on the FSI boundary, viewed from the fluid mesh.

Contour plot of the automatically-generated boundary coordinates on the FSI boundary, viewed from the solid mesh.

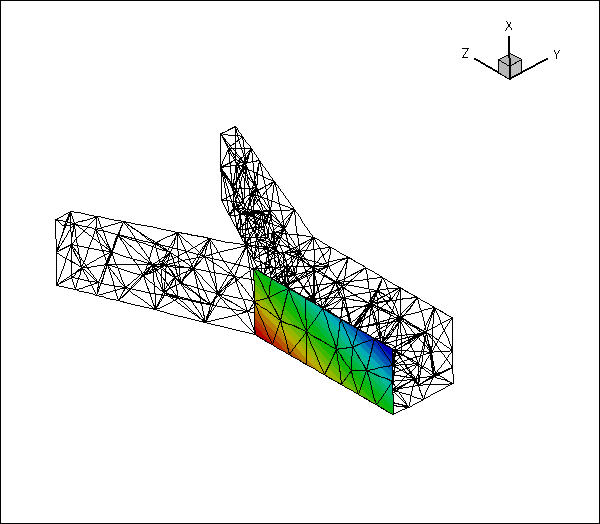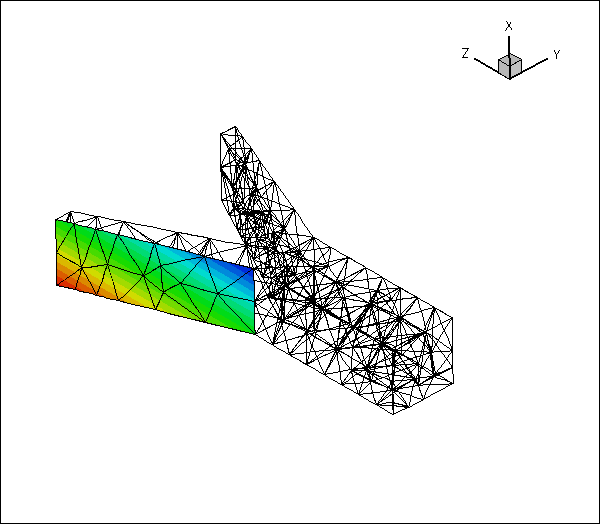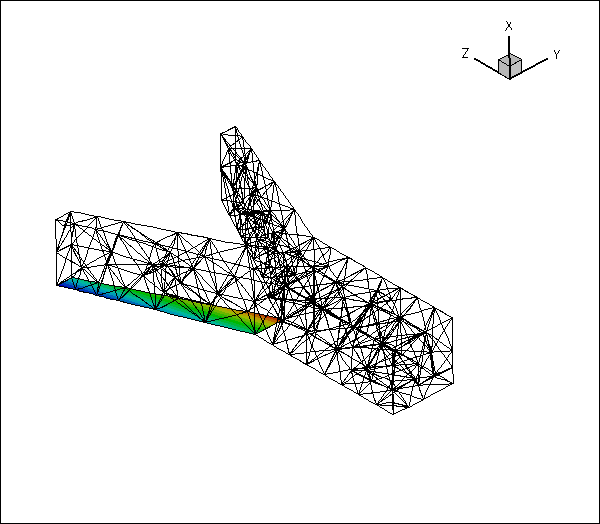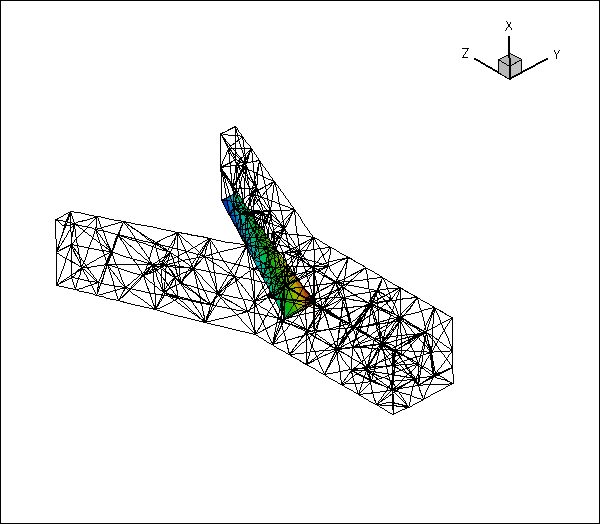
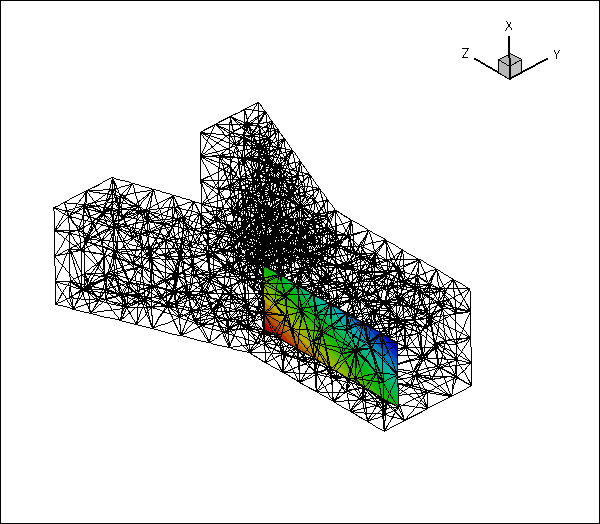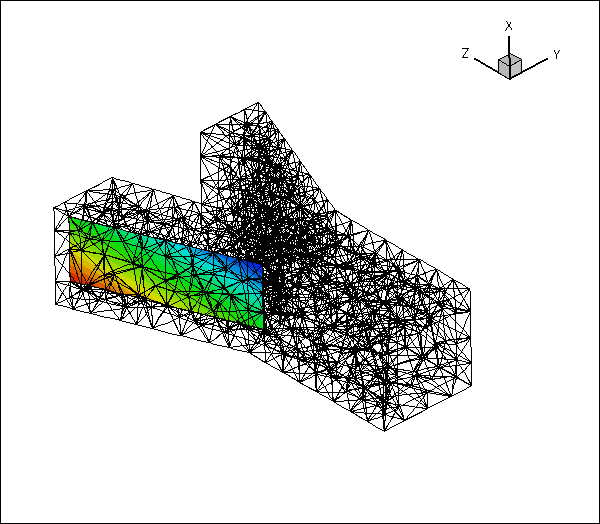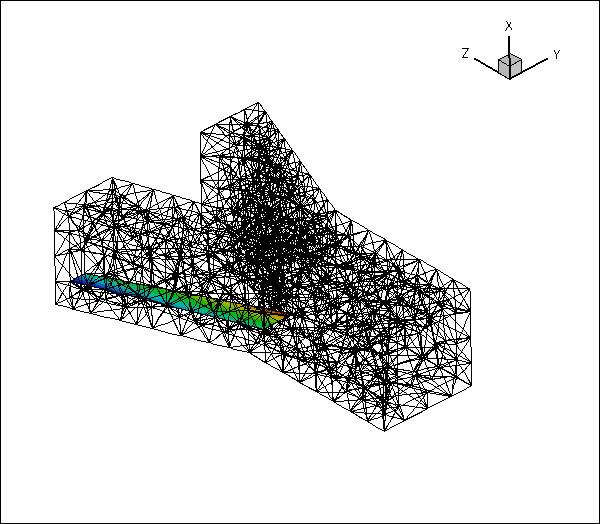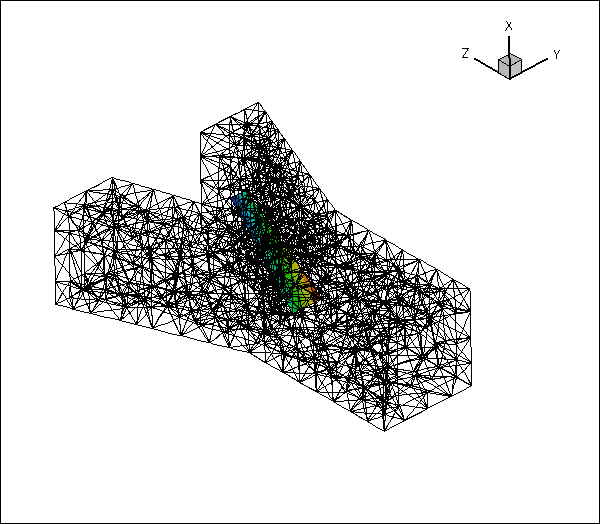
You should explore this procedure yourself as an exercise: For instance you may want to explore what happens if you don't switch the direction of the normal in the fluid mesh when generating the boundary coordinates.

Fluid and solid meshes do not have to be matching

The mesh shown in the problem sketch at the beginning of this tutorial already suggested that the fluid and solid meshes do not have to match across the FSI interface. To illustrate this point more clearly, here is the result of another computation for which we generated a much finer fluid mesh, using

tetgen -a0.05 fsi_bifurcation_fluid.poly

The resulting tetgen *.ele, *.node and *.face files can be used with same driver code.

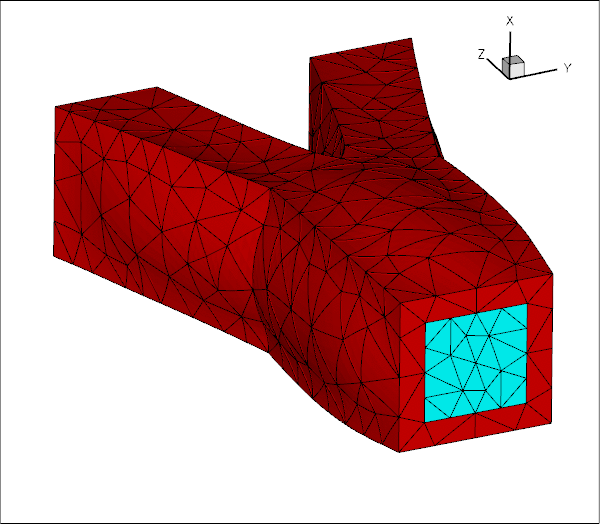
Solution computed with a finer fluid mesh.

As an exercise, generate some finer fluid and solid meshes yourself and confirm that they may be used without having to change the driver code.

What can go wrong?

Here are a few things that can (and often do) go wrong in unstructured, three-dimensional FSI problems.

The facets that define the FSI boundary don't match:

This tends to happen if the *.poly files describing the fluid and solid meshes do not use the same facets to describe the FSI interface. While we do not expect the fluid and solid meshes themselves to match, the representation of the FSI interface via facets must be consistent. A simple way to ensure consistency is to use the following procedure:
1. Write the *.poly file for the fluid mesh. Make sure that each facet is given a separate boundary ID (at least for the facets describing the FSI interface).
2. Solve a single-physics fluids problem on this mesh to check the integrity of the mesh – the solution of this problem will also give you some insight into the expected flow field.
3. Make a copy of the *.poly file for the fluid mesh and modify it to describe the solid mesh, leaving the facets that define the FSI interface unchanged. This automatically ensures that the representation of the FSI boundary from the fluid's and the solid's point of view is consistent.
4. Solve a single-physics solids problem on this mesh to check the integrity of the mesh, e.g. by applying some pressure loading on the future FSI boundary – the solution of this problem will also give you some insight into the expected wall deformation.
5. Couple the two problems, as shown in this tutorial.
As an exercise, modify the tetgen *.poly files and the driver code so that it can handle the extended domain considered in the single-physics fluids problem.
An FSI (sub-)boundary is not planar:

In an unstructured mesh, the FSI boundary will usually be represented by a large number of distinct mesh boundaries. The automatic setup of the boundary coordinates on these mesh boundaries requires them to be (individually) planar – at least in the problem's initial configuration. Provided you have followed our advice and associated each of the facets that define the FSI boundary with a different boundary ID, you should not have any problems as tetgen does not allow non-planar facets.
The solver does not converge:

A large-displacement FSI problem is a highly nonlinear problem and the provision of a good initial guess for the Newton iteration is essential. We tend to proceed as follows:
1. Follow the steps outlined above, to study the constituent single-physics problems first. This will already give you some insight into the behaviour of the problem. For instance, the solution of the single-physics Navier-Stokes equations at the desired Reynolds number may have to be computed via a parameter incrementation, starting from Stokes flow. Similarly, the study of the single-physics solid problem will reveal what load increments can be accommodated without causing the Newton iteration to diverge.
2. Combine the two single-physics problems using the steps described in this tutorial.
3. Switch off the fluid-structure interaction by
  1. setting the FSI parameter to zero,
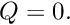
  2. commenting out the call to FSI_functions::setup_fluid_load_info_for_solid_elements(...),
  3. not creating the Lagrange-multiplier elements that enforce the solid displacements onto the fluid mesh.

This completely uncouples the two problems, although they will be solved simultaneously, allowing you to replicate the single-physics parameter studies already performed.

Now switch on the various interactions, one-by-one, while carefully validating the results at each stage. We tend to proceed as follows:
1. Solve the uncoupled problem at zero Reynolds number.
2. Increase the Reynolds number in small increments to its target value.
3. Re-enable the call to FSI_functions::setup_fluid_load_info_for_solid_elements(...) and attach the Lagrange multiplier elements but keep If the solid is not loaded by any forces/tractions other than those arising from the fluid, the solution should not change as the solid remains unloaded.
4. Gently increase the value of the FSI parameter, , remembering that it represents the ratio of the typical viscous fluid stresses to the stiffness of the solid. Hence, even relatively small values of 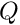tend to lead to relatively large solid displacements. Be gentle!

Source files for this tutorial

The source files for this tutorial are located in the directory:

demo_drivers/interaction/unstructured_three_d_fsi
The driver code is:

demo_drivers/interaction/unstructured_three_d_fsi/unstructured_three_d_fsi.cc

PDF file

A pdf version of this document is available.