The purpose of this tutorial is to demonstrate the solution of 3D solid mechanics problems on unstructured meshes. The problem studied here also serves as a "warm-up problem" for the corresponding fluid-structure interaction problem in which the elastic, bifurcating vessel whose deformation is studied here conveys (and is loaded by) a viscous fluid.

The problem (and results)

Here is an animation of the problem: An elastic, bifurcating vessel is loaded by an internal pressure and by gravity which acts in the negative -direction. The "ends" of the vessel are held in a fixed position. As the magnitude of the loading is increased the vessel inflates and sags downwards.

An elastic, bifurcating vessel, loaded by an internal pressure and transverse gravity.

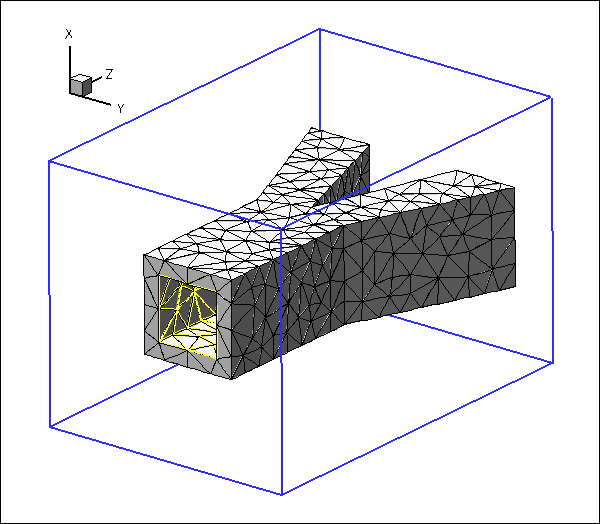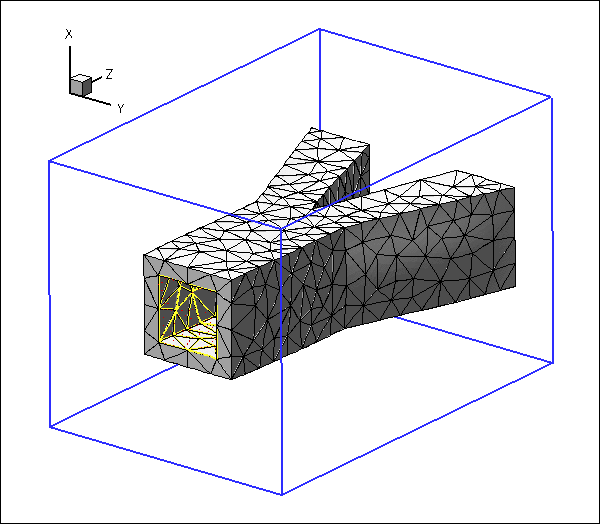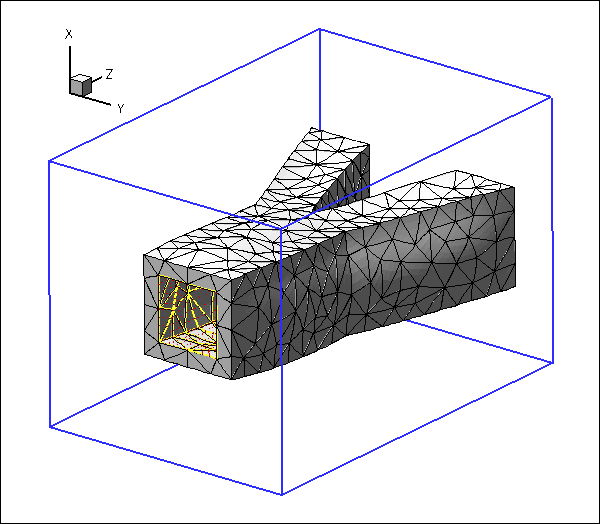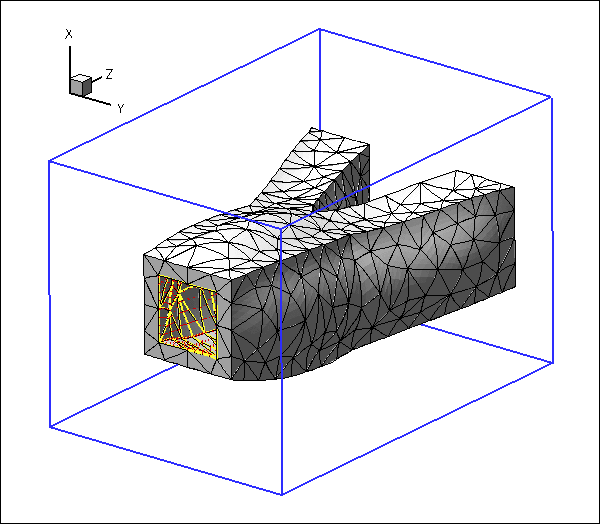
The blue frame surrounding the vessel is drawn to clarify its spatial orientation. The yellow edges show the boundaries of the internal faces via which the pressure loading is applied, and the red arrows indicate the direction and magnitude of the pressure loading.

3D unstructured mesh generation

We use Hang Si's open-source mesh generator tetgen to generate the unstructured tetrahedral mesh "offline". We then process the output files produced by
tetgen to generate an unstructured oomph-lib mesh.

Tetgen requires the specification of the domain boundaries via so-called facets – planar surface patches that are bounded by closed polygonal line segments. For simplicity, we only consider a very simplistic bifurcation, comprising three tube segments of approximately rectangular cross-section that meet at a common junction. Each of the three tube segments has four internal and four external faces. The internal and external faces are connected by three further faces at the "in- and outflow" cross-sections (using terminology that anticipates the mesh's use in the corresponding fluid-structure interaction problem), resulting in a total of 27 facets.

The 27 facets are defined in a *.poly file that specifies the position of the vertices, and identifies the facets via a "face list" that establishes their bounding vertices. Facets that have holes (e.g. the in- and outflow facets) require the specification of the hole's position. Finally, if the mesh itself has a hole (as in the current example where the vessel's lumen forms a hole in the mesh) the position of the hole must be identified by specifying the position of a single point inside that hole. The well-annotated *.poly file is located at:

demo_drivers/solid/unstructured_three_d_solid/fsi_bifurcation_solid.poly

We refer to the tetgen webpages and another oomph-lib tutorial for further details on how to create *.poly files.

Here is a plot of the domain specified by fsi_bifurcation_solid.poly. The plot was created using tetview which is distributed with tetgen .

The domain and its bounding facets.

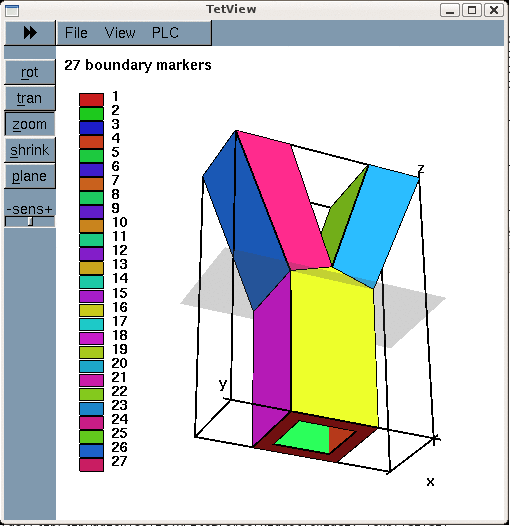
Note that we have deliberately assigned a different boundary ID to each facet. This will make the assignment of the traction boundary condition somewhat tedious as the inner surface of the vessel (where the traction is to be applied) is represented by twelve separate mesh boundaries. However, the assignment of distinct boundary IDs for the different facets is essential for the automatic generation of boundary coordinates in the corresponding fluid-structure interaction problem and is therefore strongly recommended.

Tetgen generates an unstructured volumetric mesh from the information contained in the *.poly file and writes the mesh's nodes, elements and faces in the files

These files can be used as input to oomph-lib's TetgenMesh class, using the procedure discussed in another tutorial.

The figure below shows a tetview plot of the mesh, created with a volume constraint of 0.2 (i.e. the maximum volume of each tetrahedron is guaranteed to be less than 0.2 units), using the command

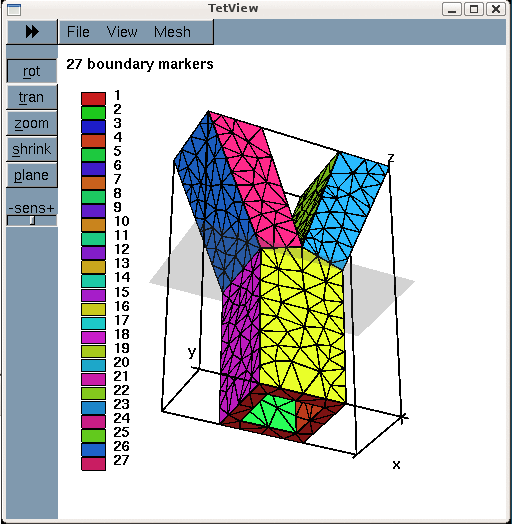
tetgen -a0.2 fsi_bifurcation_solid.poly

Plot of the mesh, generated by tetgen.

Note how tetgen has subdivided each of the 27 original facets specified in the *.poly file into a surface triangulation. The nodes and tetrahedral elements that are located on (or adjacent to) the 27 original facets inherit their boundary IDs. This will be important when we assign the boundary conditions.

Creating the mesh

We create the solid mesh by multiple inheritance from oomph-lib's TetgenMesh and the SolidMesh base class:

//=======================start_mesh========================================
/// Tetgen-based mesh upgraded to become a solid mesh
//=========================================================================
template<class ELEMENT>
class MySolidTetgenMesh : public virtual TetgenMesh<ELEMENT>, 
                       public virtual SolidMesh 
{

The constructor calls the constructor of the underlying TetgenMesh (using the *.node *.ele and *.face files created by tetgen. As usual we set the nodes' Lagrangian coordinates to their current Eulerian positions, making the current configuration stress-free.

 
public:
 
 /// Constructor: 
 MySolidTetgenMesh(const std::string& node_file_name,
                const std::string& element_file_name,
                const std::string& face_file_name,
                TimeStepper* time_stepper_pt=
                &Mesh::Default_TimeStepper) : 
  TetgenMesh<ELEMENT>(node_file_name, element_file_name,
                      face_file_name, time_stepper_pt)
  {
   //Assign the Lagrangian coordinates
   set_lagrangian_nodal_coordinates();

Finally, we identify the elements that are located next to the various mesh boundaries to facilitate the application of the traction boundary conditions.

   
   // Find elements next to boundaries
   setup_boundary_element_info();
  }
 
 /// Empty Destructor
 virtual ~MySolidTetgenMesh() { }
 
 
};

Problem parameters

As usual, we define the various problem parameters in a global namespace. We use oomph-lib's generalised Hookean constitutive law as the constitutive equation, using a Poisson's ratio of 0.3. (Recall that omitting the specification of Young's modulus, , implies that the stresses are non-dimensionalised on .)

//=======start_namespace==========================================
/// Global variables
//================================================================
namespace Global_Parameters
{
 
 /// Poisson's ratio
 double Nu=0.3;
 
 /// Create constitutive law
 ConstitutiveLaw* Constitutive_law_pt=new GeneralisedHookean(&Nu);

Next we define the gravitational body force which acts in the negative -direction,

 
 /// Non-dim gravity
 double Gravity=0.0;
 
 /// Non-dimensional gravity as body force
 void gravity(const double& time,
              const Vector<double> &xi,
              Vector<double> &b)
 {
  b[0]=-Gravity; 
  b[1]=0.0;
  b[2]=0.0;
 } // end gravity

and the pressure load, ${\bf t} = -P {\bf n}$ , that acts on internal walls of the bifurcation (note that the outer unit normal ${\bf n}$ on the wall is passed to the function).

 
 /// Uniform pressure
 double P = 0.0;
 
 /// Constant pressure load. The arguments to this function are imposed
 /// on us by the SolidTractionElements which allow the traction to 
 /// depend on the Lagrangian and Eulerian coordinates x and xi, and on the 
 /// outer unit normal to the surface. Here we only need the outer unit
 /// normal.
 void constant_pressure(const Vector<double> &xi, const Vector<double> &x,
                        const Vector<double> &n, Vector<double> &traction)
 {
  unsigned dim = traction.size();
  for(unsigned i=0;i<dim;i++)
   {
    traction[i] = -P*n[i];
   }
 } // end traction
 
 
} //end namespace

The driver code

The driver code is straightforward. We store the command line arguments, specify an output directory and create the problem object, using ten-noded tetrahedral solid mechanics elements to discretise the principle of virtual displacements.

//============================start_main==================================
/// Demonstrate how to solve an unstructured 3D solid problem
//========================================================================
int main(int argc, char **argv)
{
 // Store command line arguments
 CommandLineArgs::setup(argc,argv);
  
 // Label for output
 DocInfo doc_info;
 
 // Output directory
 doc_info.set_directory("RESLT");
  
 //Set up the problem
 UnstructuredSolidProblem<TPVDElement<3,3> > problem;

We output the initial configuration and then perform a parameter study in which we increment the gravitational body force and the pressure loads simultaneously, causing the vessel to expand and sag, as shown in the animation at the beginning of this tutorial. (As usual we perform a smaller number of steps if the code is run in self-test mode; this is indicated by a non-zero number of command line arguments.)

 
 //Output initial configuration
 problem.doc_solution(doc_info);
 doc_info.number()++;   
 
  // Parameter study
 Global_Parameters::P=0.0; 
 double g_increment=1.0e-3; 
 double p_increment=1.0e-2; 
 
 unsigned nstep=6;
 if (CommandLineArgs::Argc!=1)
  {
   std::cout << "Validation -- only doing two steps" << std::endl;
   nstep=2;
  }
 
 // Do the parameter study
 for (unsigned istep=0;istep<nstep;istep++)
  {
   // Solve the problem
   problem.newton_solve();
   
   //Output solution
   problem.doc_solution(doc_info);
   doc_info.number()++;
 
   // Bump up load
   Global_Parameters::Gravity+=g_increment;
   Global_Parameters::P+=p_increment; 
   
  }
 
} // end main

The Problem class

The Problem class has the usual member functions, and provides storage for the various sub-meshes – the bulk mesh of 3D solid elements and the meshes of 2D solid traction elements that apply the pressure load to the internal boundaries of the vessel.

//=============start_problem===========================================
/// Unstructured solid problem
//=====================================================================
template<class ELEMENT>
class UnstructuredSolidProblem : public Problem
{
 
public:
 
 /// Constructor: 
 UnstructuredSolidProblem();
 
 /// Destructor (empty)
 ~UnstructuredSolidProblem(){}
 
 /// Doc the solution
 void doc_solution(DocInfo& doc_info);
 
private:
 
 /// Create traction elements
 void create_traction_elements();
 
 /// Bulk solid mesh
 MySolidTetgenMesh<ELEMENT>* Solid_mesh_pt;
 
 /// Meshes of traction elements
 Vector<SolidMesh*> Solid_traction_mesh_pt;

The two vectors Pinned_solid_boundary_id and Solid_traction_boundary_id are used to store the IDs of mesh boundaries that make up the in- and outflow cross-sections (where the bifurcation is pinned), and the internal boundaries (where the pressure load has to be applied). Recall that tetgen requires the domain boundaries to be specified as a collection of planar facets. Boundary of interest in the computation, such as the "internal boundary of the bifurcation", therefore tend to comprise multiple distinct mesh boundaries.

 
 /// IDs of solid mesh boundaries where displacements are pinned
 Vector<unsigned> Pinned_solid_boundary_id;
 
 /// IDs of solid mesh boundaries which make up the traction interface
 Vector<unsigned> Solid_traction_boundary_id;
 
};

The Problem constructor

We start by building the bulk mesh, using the files created by tetgen :

//=============start_constructor==========================================
/// Constructor for unstructured solid problem
//========================================================================
template<class ELEMENT>
UnstructuredSolidProblem<ELEMENT>::UnstructuredSolidProblem()
{ 
 
  //Create solid bulk mesh
 string node_file_name="fsi_bifurcation_solid.1.node";
 string element_file_name="fsi_bifurcation_solid.1.ele";
 string face_file_name="fsi_bifurcation_solid.1.face";
 Solid_mesh_pt =  new MySolidTetgenMesh<ELEMENT>(node_file_name,
                                              element_file_name,
                                              face_file_name);

Next we specify the IDs of the tetgen boundaries that form part of specific domain boundaries in our problem. Boundaries 0, 1 and 2 are the in- and outflow faces along which the solid is pinned. (See the specification of the boundaries in fsi_bifurcation_solid.poly and/or check the boundary enumeration using tetview as shown in the tetview plot of the domain boundaries at the beginning of this tutorial.)

 
 // The following IDs corresponds to the boundary IDs specified in
 // the *.poly file from which tetgen generated the unstructured mesh.
 
 /// IDs of solid mesh boundaries where displacements are pinned
 Pinned_solid_boundary_id.resize(3);
 Pinned_solid_boundary_id[0]=0;
 Pinned_solid_boundary_id[1]=1;
 Pinned_solid_boundary_id[2]=2;

Similarly, boundaries 3 to 15 are the faces that define the internal boundary of the bifurcation, i.e. the boundary along which we have to apply the pressure load:

 
  // The solid mesh boundaries where an internal pressure is applied
 Solid_traction_boundary_id.resize(12);
 for (unsigned i=0;i<12;i++)
  {
   Solid_traction_boundary_id[i]=i+3;
  }

We apply the boundary conditions by pinning the displacements of all nodes that are located on the in- and outflow faces, and document their positions.

 
 
 // Apply BCs for solid
 //--------------------
 
 // Doc pinned solid nodes
 std::ofstream bc_file("RESLT/pinned_solid_nodes.dat");
 
 // Pin positions at inflow boundary (boundaries 0 and 1)
 unsigned n=Pinned_solid_boundary_id.size();
 for (unsigned i=0;i<n;i++)
  {
   // Get boundary ID
   unsigned b=Pinned_solid_boundary_id[i];
   unsigned num_nod= Solid_mesh_pt->nboundary_node(b);  
   for (unsigned inod=0;inod<num_nod;inod++)
    {    
     // Get node
     SolidNode* nod_pt=Solid_mesh_pt->boundary_node_pt(b,inod);
     
     // Pin all directions
     for (unsigned i=0;i<3;i++)
      {
       nod_pt->pin_position(i);
       
       // ...and doc it as pinned
       bc_file << nod_pt->x(i) << " ";
      }
     
     bc_file << std::endl;
    }
  }
 bc_file.close();

We complete the build of the elements by setting the pointer to the constitutive equation and the body force.

 
 
 
 // Complete the build of all elements so they are fully functional
 //----------------------------------------------------------------
 unsigned n_element = Solid_mesh_pt->nelement();
 for(unsigned i=0;i<n_element;i++)
  {
   //Cast to a solid element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(
    Solid_mesh_pt->element_pt(i));
   
   // Set the constitutive law   
   el_pt->constitutive_law_pt() =
    Global_Parameters::Constitutive_law_pt;
   
   //Set the body force
   el_pt->body_force_fct_pt() = Global_Parameters::gravity;
  }

Next we create the traction elements, attaching them to the "bulk" solid elements that are adjacent to the boundaries that constitute the inside of the vessel.

 
 
 // Create traction elements
 //-------------------------
 
 // Create meshes of traction elements
 n=Solid_traction_boundary_id.size();
 Solid_traction_mesh_pt.resize(n);
 for (unsigned i=0;i<n;i++)
  {
   Solid_traction_mesh_pt[i]=new SolidMesh;
  }
 
 // Build the traction elements
 create_traction_elements();

Finally, we add the various meshes as sub-meshes to the Problem, build the global mesh, and assign the equation numbers.

 
 
 // Combine the lot
 //----------------
 
 // The solid bulk mesh
 add_sub_mesh(Solid_mesh_pt);
 
 // The solid traction meshes
 n=Solid_traction_boundary_id.size();
 for (unsigned i=0;i<n;i++)
  {
   add_sub_mesh(Solid_traction_mesh_pt[i]);
  }
 
 // Build global mesh
 build_global_mesh();
 
 // Setup equation numbering scheme
 std::cout <<"Number of equations: " << assign_eqn_numbers() << std::endl; 
 
} // end constructor

Creating the traction elements

The helper function create_traction_elements() does exactly what it says: It loops over the bulk elements that are adjacent to the inner surface of the vessel, and attaches SolidTractionElements to the appropriate faces. We store the pointers to the newly-created traction elements in separate meshes and specify the function pointer to the load function.

 
 
 
//============start_of_create_traction_elements==========================
/// Create traction elements 
//=======================================================================
template<class ELEMENT>
void UnstructuredSolidProblem<ELEMENT>::create_traction_elements()
{
 
 // Loop over traction boundaries
 unsigned n=Solid_traction_boundary_id.size();
 for (unsigned i=0;i<n;i++)
  {
   // Get boundary ID
   unsigned b=Solid_traction_boundary_id[i];
   
   // How many bulk elements are adjacent to boundary b?
   unsigned n_element = Solid_mesh_pt->nboundary_element(b);
   
   // Loop over the bulk elements adjacent to boundary b
   for(unsigned e=0;e<n_element;e++)
    {
     // Get pointer to the bulk element that is adjacent to boundary b
     ELEMENT* bulk_elem_pt = dynamic_cast<ELEMENT*>(
      Solid_mesh_pt->boundary_element_pt(b,e));
     
     //What is the index of the face of the element e along boundary b
     int face_index = Solid_mesh_pt->face_index_at_boundary(b,e);
     
     // Create new element 
     SolidTractionElement<ELEMENT>* el_pt=
      new SolidTractionElement<ELEMENT>(bulk_elem_pt,face_index);
     
     // Add it to the mesh
     Solid_traction_mesh_pt[i]->add_element_pt(el_pt);
     
     //Set the traction function
     el_pt->traction_fct_pt() = Global_Parameters::constant_pressure;
    }
  }
 
} // end of create_traction_elements

Post-processing

The post-processing routine outputs the deformed domain shape and the applied traction.

 
 
 
//========================================================================
/// Doc the solution
//========================================================================
template<class ELEMENT>
void UnstructuredSolidProblem<ELEMENT>::doc_solution(DocInfo& doc_info)
{ 
 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned npts;
 npts=5;
 
 // Output solid solution
 //-----------------------
 sprintf(filename,"%s/solid_soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Solid_mesh_pt->output(some_file,npts);
 some_file.close();
 
    
 // Output traction
 //----------------
 sprintf(filename,"%s/traction%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 unsigned n=Solid_traction_boundary_id.size();
 for (unsigned i=0;i<n;i++)
  {
   Solid_traction_mesh_pt[i]->output(some_file,npts);
  }
 some_file.close();
 
} // end doc

Comments and Exercises

Identification/assignment of mesh boundaries

This tutorial shows that the use of unstructured 3D meshes for solid mechanics problems is extremely straightforward. The only aspect that requires some care (and not just for solid mechanics applications) is the correct identification/assignment of domain boundaries. The fact that we documented the position of the pinned nodes in the driver code suggests (correctly!) that we managed to get both assignments (slightly) wrong when we first generated the mesh and wrote the corresponding driver code. As usual, it pays off to be as a paranoid as possible! Ignore this advice at your own risk...

Here is a plot of the position of the pinned solid nodes

Plot of the pinned solid nodes.

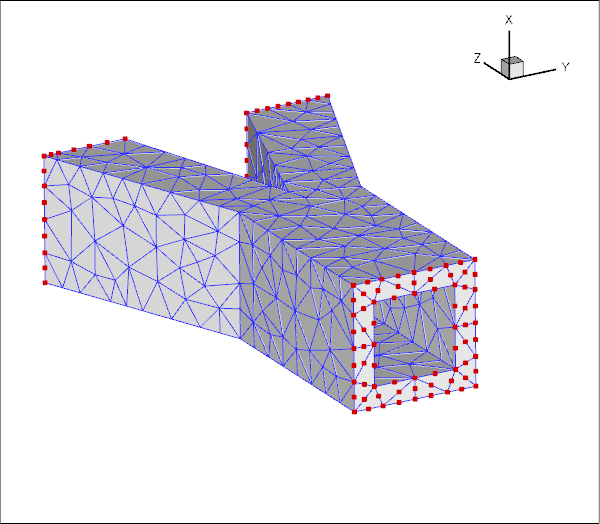
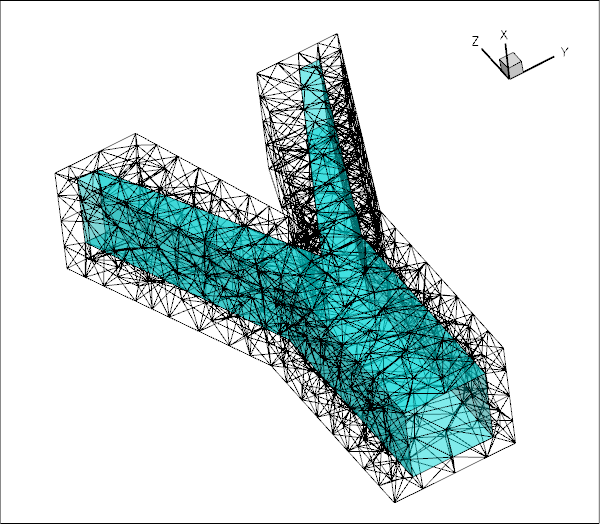
and here's a plot showing the SolidTractionElements attached to the inside of the vessel:

Plot of the SolidTractionElements that apply the pressure load to the inner surface of the vessel.

Exercise: Try it yourself

Experiment with the tetgen -based mesh generation by modifying the *.poly file used in this example to different vessel geometries.

Source files for this tutorial

The source files for this tutorial are located in the directory:

demo_drivers/solid/unstructured_three_d_solid/
The driver codes are:

demo_drivers/solid/unstructured_three_d_solid/unstructured_three_d_solid.cc and demo_drivers/solid/unstructured_three_d_solid/unstructured_three_d_solid.cc

PDF file

A pdf version of this document is available.