In the previous example we considered a two-dimensional free surface Navier–Stokes problem. The free surface was deformed to a prescribed shape and then allowed to relax. In this example we consider the relaxation of an interface between two viscous fluids.

Implementation

The extension from a single fluid problem to one involving two fluids separated by an interface is very straightforward. As oomph-lib's Navier–Stokes elements are based on the Arbitrary Lagrangian Eulerian form of the equations, and can therefore be used to solve problems in moving domains, we can discretise the domain using a rectangular mesh containing an additional boundary corresponding to the position of the interface. The construction of such a mesh is described below. We also require a method of distinguishing between (and assigning) the physical properties of the two fluid layers.

Boundary conditions at the interface

A discussion of the theory and implementation of the boundary conditions at a free surface is given in the previous example, where we showed that the dynamic boundary condition is given by

$\tau_{ij}^{[2]} \, n_j^{[1]} = \tau_{ij}^{[1]} \, n_j^{[1]} + \frac{1}{Ca} \, \kappa \, n_i^{[1]}.$

Here $\tau_{ij}^{[1]}$ and $\tau_{ij}^{[2]}$ are the stress tensors in the ‘lower’ and ‘upper’ fluids respectively, $n_j^{[1]}$ is the unit normal pointing out of the ‘lower’ fluid and is the Capillary number.

The interface conditions in this two-fluid example are implemented in an almost identical way to the single layer case. We employ the same pseudo-solid node-update strategy, where the interior mesh is treated as a fictitious elastic solid and thus the (unknown) nodal positions can be determined by solving a solid mechanics problem. The deformation of the free surface boundary itself is imposed by introducing a a field of Lagrange multipliers at the interface, and the equation associated with these additional unknowns is the kinematic condition. In the single layer case this equation is discretised by attaching FaceElements to the boundaries of the ‘bulk’ elements that are adjacent to the free surface. In this two-layer example we attach the same FaceElements to only those ‘bulk’ elements which are in the ‘lower’ fluid (and have boundaries adjacent to the interface). These same FaceElements are also responsible for adding the surface tension contributions to the momentum equations that arise through the application of the dynamic boundary condition. We note that since we are solving the Navier–Stokes equations on either side of the interface we do not specify an external pressure, a step that was necessary in the single layer case.

The other difference between this problem and the previous example is that we shall be solving this one using spatial adaptivity. We refer to another tutorial for a discussion of how to apply boundary conditions in such problems.

Distinguishing between the two fluids

In a problem containing a single fluid, the definitions of the Reynolds number, Strouhal number, Capillary number and so on are based on the physical properties of that fluid, as well as the geometry of the problem and typical timescales. In our discussion of the non-dimensionalisation of the Navier–Stokes equations we describe how the various dimensionless parameters are defined in terms of a reference density, $\rho_{ext}$ , and a reference viscosity, $\mu_{ext}$ . We can then define two dimensionless ratios, $R_\rho$ and $R_\mu$ , which describe a particular fluid's density $\rho$ and kinematic viscosity $\mu$ relative to these reference quantities:

$R_\rho = \frac{\rho}{\rho_{ref}} \qquad ; \qquad R_\mu = \frac{\mu}{\mu_{ref}}.$

oomph-lib's implementation of the Navier–Stokes equations contains these ratios in the appropriate terms. They default to one but can be set to other values via the member functions density_ratio_pt() and viscosity_ratio_pt() in each element.

It is convenient to choose one of the fluids in this problem to be the ‘reference fluid’ on which the dimensionless parameters are based. We choose the lower fluid (fluid 1), and hence the density $\rho^{[1]}$ and viscosity $\mu^{[1]}$ of this fluid are identically equal to $\rho_{ref}$ and $\mu_{ref}$ (and thus $R_\rho^{[1]} = R_\mu^{[1]} = 1$ ). We can now control the relative density and viscosity of the upper fluid to the lower fluid using the ratios $R_\rho^{[2]} = \rho^{[2]}/\rho_{ref}$ and $R_\mu^{[2]} = \mu^{[2]}/\mu_{ref}$ respectively. For simplicity we will from now on refer to $R_\rho^{[2]}$ simply as $R_\rho$ and to $R_\mu^{[2]}$ as $R_\mu$ .

The example problem

We will illustrate the solution of the unsteady two-dimensional Navier–Stokes equations using the example of a distorted interface between two viscous fluids which is allowed to relax. The domain is periodic in the direction.

The 2D unsteady Navier–Stokes equations either side of a distorted interface.

Solve

$Re\left(St\frac{\partial u_i}{\partial t} + \ u_j\frac{\partial u_i}{\partial x_j}\right) = - \frac{\partial p}{\partial x_i} + \frac{Re}{Fr}G_i + \frac{\partial }{\partial x_j} \left[ \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right] \ \ \ \ \ \ \ \ \ \ (1)$

and

$\frac{\partial u_i}{\partial x_i} = 0 \ \ \ \ \ \ \ \ \ \ (2)$

in the ‘lower’ fluid, and

$R_\rho Re\left(St\frac{\partial u_i}{\partial t} + \ u_j\frac{\partial u_i}{\partial x_j}\right) = - \frac{\partial p}{\partial x_i} + R_\rho \frac{Re}{Fr}G_i + \frac{\partial }{\partial x_j} \left[R_\mu \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) \right] \ \ \ \ \ \ \ \ \ \ (3)$

and

$\frac{\partial u_i}{\partial x_i} = 0 \ \ \ \ \ \ \ \ \ \ (4)$

in the ‘upper’ fluid. Gravity acts in the negative direction and so and . The governing equations are subject to the no slip boundary conditions

$u_1 = u_2 = 0 \ \ \ \ \ \ \ \ \ \ (5)$

on the top ( ) and bottom ( ) solid boundaries and the symmetry boundary conditions

$u_1 = 0 \ \ \ \ \ \ \ \ \ \ (6)$

on the left ( ) and right ( ) boundaries.

We denote the position vector to the interface between the two fluids by $\mathbf{R}$ , which is subject to the kinematic condition

$\left(u_i - St\, \frac{\partial R_i}{\partial t}\right) n_i = 0, \ \ \ \ \ \ \ \ \ \ (7)$

and the dynamic condition

$\tau_{ij}^{[2]} \, n_j^{[1]} = \tau_{ij}^{[1]} \, n_j^{[1]} + \frac{1}{Ca} \, \kappa \, n_i^{[1]}. \ \ \ \ \ \ \ \ \ \ (8)$

The stress tensor in the ‘lower’ fluid is defined as

$\tau_{ij}^{[1]} = -p^{[1]} \, \delta_{ij} + \left(\frac{\partial u^{[1]}_i}{\partial x_j} + \frac{\partial u^{[1]}_j}{\partial x_i}\right), \ \ \ \ \ \ \ \ \ \ (9)$

and that in the ‘upper’ fluid is defined as

$\tau_{ij}^{[2]} = -p^{[2]} \, \delta_{ij} + R_\mu \left(\frac{\partial u^{[2]}_i}{\partial x_j} + \frac{\partial u^{[2]}_j}{\partial x_i}\right). \ \ \ \ \ \ \ \ \ \ (10)$

The initial shape of the interface is defined by

$\mathbf{R} = x_1 \, \mathbf{i} + \left[ 1.0 + \epsilon\cos\left( 2 n \pi x_1 \right)\right] \, \mathbf{j}, \ \ \ \ \ \ \ \ \ \ (11)$

where $\epsilon$ is the amplitude of the initial deflection and is an integer.

Results

The figure below shows a contour plot of the pressure distribution taken from an animation of the flow field, for the parameters $Re = Re \, St = Re/Fr = 5.0$ , $R_\rho = 0.5$ , $R_\mu = 0.1$ and .

Pressure contour plot for the relaxing interface problem.

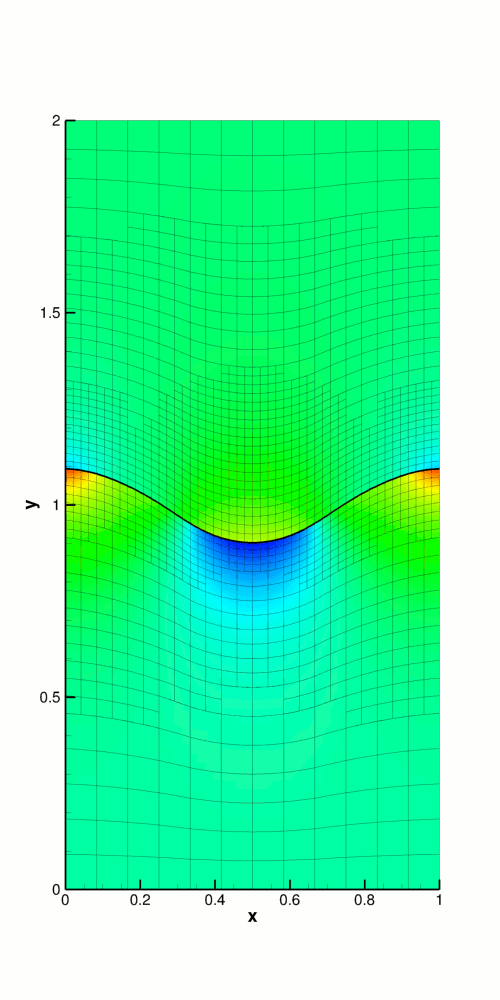
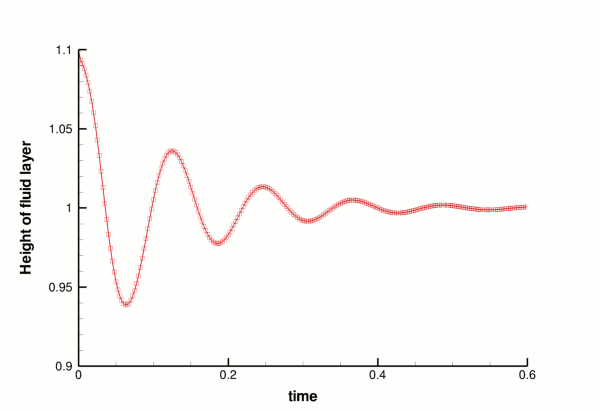
The restoring forces of surface tension and gravitational acceleration act to revert the interface to its undeformed flat state. The interface oscillates up and down, but the motion is damped as the energy in the system is dissipated through viscous forces. Eventually the interface settles down to its equilibrium position, as can be seen in the following time-trace of the height of the interface at the left-hand edge of the domain ( ).

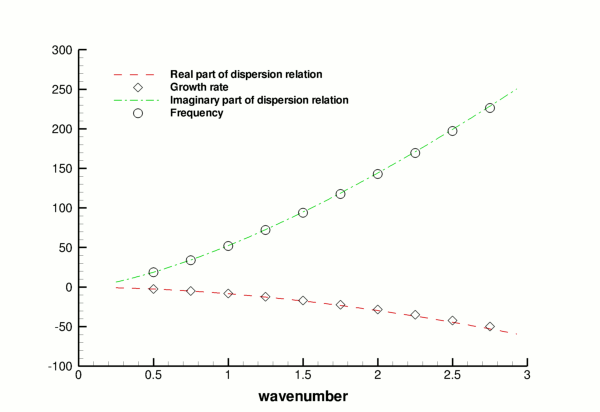
Time-trace of the height of the interface at the point x_1 = 0.

Validation

The free surface boundary conditions for the Cartesian Navier–Stokes equations have been validated against an analytical test case, and we present the results in the figure below. For sufficiently small amplitudes, $\epsilon \ll 1$ , we can linearise the governing equations and obtain a dispersion relation $\lambda(k)$ , the derivation of which is discussed in the previous tutorial. The only difference in this two layer case is that the linear system which needs to be solved contains nine unknowns rather than five, since the two fluids have different properties. The real and imaginary parts of $\lambda$ correspond to the growth rate and the frequency of the oscillating interface respectively, and can be compared to numerical results computed for given values of the wavenumber . We choose an initial deflection amplitude of $\epsilon = 0.01$ and determine the growth rate and frequency of the oscillation from a time-trace of the left-hand edge of the interface.

Validation of the code (points) by comparison with an analytical dispersion relation (lines).

Global parameters and functions

As in the previous example, we use a namespace to define the dimensionless parameters , , and . The pseudo-solid mesh is governed by a generalised Hookean constitutive law which requires the definition of the Poisson ratio, $\nu$ , and we create a vector which will define the direction in which gravity acts. Because this is a two-fluid problem, we also need to define the density ratio $R_{\rho} = \rho^{[2]}/\rho^{[1]}$ and viscosity ratio $R_{\mu} = \mu^{[2]}/\mu^{[1]}$ of the two fluids.

//==start_of_namespace====================================================
/// Namespace for physical parameters
//========================================================================
namespace Global_Physical_Variables
{
 
 /// Reynolds number
 double Re = 5.0;
 
 /// Strouhal number
 double St = 1.0;
 
 /// Womersley number (Reynolds x Strouhal)
 double ReSt = 5.0;
 
 /// Product of Reynolds number and inverse of Froude number
 double ReInvFr = 5.0;
 
 /// Ratio of viscosity in upper fluid to viscosity in lower
 /// fluid. Reynolds number etc. is based on viscosity in lower fluid.
 double Viscosity_Ratio = 0.1;
 
 /// Ratio of density in upper fluid to density in lower
 /// fluid. Reynolds number etc. is based on density in lower fluid.
 double Density_Ratio = 0.5;
 
 /// Capillary number
 double Ca = 0.01;
 
 /// Direction of gravity
 Vector<double> G(2);
 
 /// Pseudo-solid Poisson ratio
 double Nu = 0.1;
 
} // End of namespace

The driver code

The driver code is very similar to the previous example. We define a command line flag which allows us to run a ‘validation’ version of the code (for oomph-lib's self-testing routines) and check that the non-dimensional quantities provided in the Global_Physical_Variables namespace are self-consistent.

//==start_of_main=========================================================
/// Driver code for two-dimensional two fluid interface problem
//========================================================================
int main(int argc, char* argv[]) 
{
 // Store command line arguments
 CommandLineArgs::setup(argc,argv);
 
 // -----------------------------------------------------------------
 // Define possible command line arguments and parse the ones that
 // were actually specified
 // -----------------------------------------------------------------
 
 // Are we performing a validation run?
 CommandLineArgs::specify_command_line_flag("--validation");
 
 // Parse command line
 CommandLineArgs::parse_and_assign();
 
 // Doc what has actually been specified on the command line
 CommandLineArgs::doc_specified_flags();
 
 // Check that definition of Womersley number is consistent with those
 // of the Reynolds and Strouhal numbers
 if(Global_Physical_Variables::ReSt !=
    Global_Physical_Variables::Re*Global_Physical_Variables::St)
  {
   std::ostringstream error_stream;
   error_stream << "Definition of Global_Physical_Variables::ReSt is "
                << "inconsistant with those\n"
                << "of Global_Physical_Variables::Re and "
                << "Global_Physical_Variables::St." << std::endl;
   throw OomphLibError(error_stream.str(),
                       OOMPH_CURRENT_FUNCTION,OOMPH_EXCEPTION_LOCATION);
  }

Next we specify the duration of the simulation and the size of the timestep. If we are running the code as a self-test, we set the length of the simulation such that only two timesteps are taken. The direction in which gravity acts is defined to be vertically downwards.

 /// Maximum time
 double t_max = 0.6;
 
 /// Duration of timestep
 const double dt = 0.0025;
 
 // If we are doing validation run, use smaller number of timesteps
 if(CommandLineArgs::command_line_flag_has_been_set("--validation"))
  {
   t_max = 0.005;
  }
 
 // Set direction of gravity (vertically downwards)
 Global_Physical_Variables::G[0] = 0.0;
 Global_Physical_Variables::G[1] = -1.0;

Finally, we build the problem using the ‘pseudo-solid’ version of RefineableQCrouzeixRaviartElements and the BDF<2> timestepper, before calling unsteady_run(...). This function solves the system at each timestep using the Problem::unsteady_newton_solve(...) function before documenting the result.

 // Set up the elastic test problem with QCrouzeixRaviartElements,
 // using the BDF<2> timestepper
 InterfaceProblem<RefineablePseudoSolidNodeUpdateElement<
 RefineableQCrouzeixRaviartElement<2>,RefineableQPVDElement<2,3> >, BDF<2> >
  problem;
 
 // Run the unsteady simulation
 problem.unsteady_run(t_max,dt);
 
} // End of main

The mesh class

In the previous example we employed oomph-lib's ElasticRectangularQuadMesh. If we wanted to solve the same single-layer problem but with spatial adaptivity we would simply use that mesh's refineable counterpart, the ElasticRefineableRectangularQuadMesh. For this two-layer problem, however, it is convenient to define a new mesh class which contains an additional ‘boundary’ which corresponds to the interface between the two fluids. We start by defining the new class (which is templated by the element type) and inheriting from ElasticRefineableRectangularQuadMesh.

//==start_of_specific_mesh_class==========================================
/// Two layer mesh which employs a pseudo-solid node-update strategy.
/// This class is essentially a wrapper to an 
/// ElasticRefineableRectangularQuadMesh, with an additional boundary
/// to represent the interface between the two fluid layers.
//========================================================================
template <class ELEMENT>
class ElasticRefineableTwoLayerMesh :
 public virtual ElasticRefineableRectangularQuadMesh<ELEMENT>
{

Next we define the mesh's constructor. We pass it the usual parameters, including a boolean flag which indicates whether or not the mesh is periodic in the direction.

public:
 
 /// Constructor: Pass number of elements in x-direction, number of
 /// elements in y-direction in bottom and top layer, respectively,
 /// axial length and height of top and bottom layers, a boolean
 /// flag to make the mesh periodic in the x-direction, and pointer 
 /// to timestepper (defaults to Steady timestepper)
 ElasticRefineableTwoLayerMesh(const unsigned &nx, 
                               const unsigned &ny1,
                               const unsigned &ny2, 
                               const double &lx,
                               const double &h1,
                               const double &h2,
                               const bool& periodic_in_x,
                               TimeStepper* time_stepper_pt=
                               &Mesh::Default_TimeStepper)
  : RectangularQuadMesh<ELEMENT>(nx,ny1+ny2,lx,h1+h2,
                                 periodic_in_x,time_stepper_pt),
    ElasticRectangularQuadMesh<ELEMENT>(nx,ny1+ny2,lx,h1+h2,
                                        periodic_in_x,time_stepper_pt),
    ElasticRefineableRectangularQuadMesh<ELEMENT>(nx,ny1+ny2,lx,h1+h2,
                                                  periodic_in_x,
                                                  time_stepper_pt)
  {

We have so far created an ElasticRefineableRectangularQuadMesh, which has four boundaries corresponding to the edges of our problem's domain. We wish to define a fifth boundary which corresponds to the interface position. First we set the number of boundaries to five and then convert all the Nodes which lie on the interface into BoundaryNodes. These are then added to the fifth boundary.

   // Set the number of boundaries to 5
   this->set_nboundary(5);
 
   // Loop over horizontal elements
   for(unsigned e=0;e<nx;e++)
    {
     // Get pointer to element in lower fluid adjacent to interface
     FiniteElement* el_pt = this->finite_element_pt(nx*(ny1-1)+e);
 
     // Determine number of nodes in this element
     const unsigned n_node = el_pt->nnode();
 
     // The last three nodes in this element are those on the interface.
     // Loop over these nodes and convert them to boundary nodes.
     for(unsigned n=0;n<3;n++)
      {
       Node* nod_pt = el_pt->node_pt(n_node-3+n);
       this->convert_to_boundary_node(nod_pt);
       this->add_boundary_node(4,nod_pt);
      }
    } // End of loop over horizontal elements

All that remains is to set up the boundary element information. This is required so that we can easily have access to the bulk elements either side of this new boundary.

   // Set up the boundary element information
   this->setup_boundary_element_info();
  }
 
}; // End of specific mesh class

The problem class

This is very similar to the problem class in the previous example, with a few modifications. Because we shall use spatial adaptivity when solving this problem, we define the following two functions, which will be called before and after mesh adaptation.

 /// Strip off the interface elements before adapting the bulk mesh
 void actions_before_adapt();
 
 /// Rebuild the mesh of interface elements after adapting the bulk mesh
 void actions_after_adapt();

These two functions will employ two helper functions which are responsible for the creation and deletion of the interface elements.

 /// Create the 1d interface elements
 void create_interface_elements();
 
 /// Delete the 1d interface elements
 void delete_interface_elements();

The final modification to the problem class is the addition of a helper function which pins a pressure value in a specified element and assigns a specific value.

 /// Fix pressure in element e at pressure dof pdof and set to pvalue
 void fix_pressure(const unsigned &e,
                   const unsigned &pdof, 
                   const double &pvalue)
  {
   // Fix the pressure at that element
   dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(e))->
                          fix_pressure(pdof,pvalue);
  }

The problem constructor

The constructor starts by building the timestepper and setting the dimensions of the mesh. The number of elements in the and directions in both fluid layers are specified.

//==start_of_constructor==================================================
/// Constructor for two fluid interface problem
//========================================================================
template <class ELEMENT, class TIMESTEPPER>
InterfaceProblem<ELEMENT,TIMESTEPPER>::
InterfaceProblem()
{
 // Allocate the timestepper (this constructs the time object as well)
 add_time_stepper_pt(new TIMESTEPPER);
 
 // Define number of elements in x direction
 const unsigned n_x = 3;
   
 // Define number of elements in y direction in lower fluid (fluid 1)
 const unsigned n_y1 = 3;
 
 // Define number of elements in y direction in upper fluid (fluid 2)
 const unsigned n_y2 = 3;
 
 // Define width of domain and store as class member data
 const double l_x = 1.0;
 this->Lx = l_x;
 
 // Define height of lower fluid layer
 const double h1 = 1.0;
 
 // Define height of upper fluid layer
 const double h2 = 1.0;

Next we build the bulk mesh, create an error estimator for the problem and set the maximum refinement level.

 // Build and assign the "bulk" mesh (the "true" boolean flag tells
 // the mesh constructor that the domain is periodic in x)
 Bulk_mesh_pt = new ElasticRefineableTwoLayerMesh<ELEMENT>
  (n_x,n_y1,n_y2,l_x,h1,h2,true,time_stepper_pt());
 
 // Create and set the error estimator for spatial adaptivity
 Bulk_mesh_pt->spatial_error_estimator_pt() = new Z2ErrorEstimator;
 
 // Set the maximum refinement level for the mesh to 4
 Bulk_mesh_pt->max_refinement_level() = 4;

An empty surface mesh is created and then populated with a call to create_interface_elements(). The bulk and surface meshes are then combined to form the global mesh.

 // Create the "surface" mesh that will contain only the interface
 // elements. The constructor just creates the mesh without giving
 // it any elements, nodes, etc.
 Surface_mesh_pt = new Mesh;
 
 // Create interface elements at the boundary between the two fluids,
 // and add them to the surface mesh
 create_interface_elements();
 
 // Add the two sub meshes to the problem
 add_sub_mesh(Bulk_mesh_pt);
 add_sub_mesh(Surface_mesh_pt);
 
 // Combine all sub-meshes into a single mesh
 build_global_mesh();

On the top and bottom boundaries ( and ) we apply the no-slip condition by pinning both velocity components. On the left and right symmetry boundaries ( and ) we pin the component of the velocity but leave the component unconstrained. We pin the vertical displacement of the nodes on the solid boundaries (since these must remain stationary) and pin the horizontal displacement of all nodes in the mesh.

 // Set the boundary conditions for this problem
 // --------------------------------------------
 
 // All values are free by default -- just pin the ones that have
 // Dirichlet conditions here
 
 // Determine number of mesh boundaries
 const unsigned n_boundary = Bulk_mesh_pt->nboundary();
 
 // Loop over mesh boundaries
 for(unsigned b=0;b<n_boundary;b++)
  {
   // Determine number of nodes on boundary b
   const unsigned n_node = Bulk_mesh_pt->nboundary_node(b);
 
   // Loop over nodes on boundary b
   for(unsigned n=0;n<n_node;n++)
    {
     // Fluid boundary conditions:
     // --------------------------
 
     // Pin x-component of velocity (no slip/penetration)
     // on all boundaries other than the interface (b=4)
     if(b!=4) { Bulk_mesh_pt->boundary_node_pt(b,n)->pin(0); }
 
     // Pin y-component of velocity on both solid boundaries (no penetration)
     if(b==0 || b==2) { Bulk_mesh_pt->boundary_node_pt(b,n)->pin(1); }
 
     // Solid boundary conditions:
     // --------------------------
 
     // Pin vertical mesh position on both solid boundaries (no penetration)
     if(b==0 || b==2) { Bulk_mesh_pt->boundary_node_pt(b,n)->pin_position(1); }
 
    } // End of loop over nodes on boundary b
  } // End of loop over mesh boundaries
 
 // Pin horizontal position of all nodes
 const unsigned n_node = Bulk_mesh_pt->nnode();
 for(unsigned n=0;n<n_node;n++) { Bulk_mesh_pt->node_pt(n)->pin_position(0); }

Next we create a generalised Hookean constitutive equation for the pseudo-solid mesh. This constitutive equation is discussed in another tutorial.

// Define a constitutive law for the solid equations: generalised Hookean

Constitutive_law_pt = new GeneralisedHookean(&Global_Physical_Variables::Nu);

Problem_Parameter::Constitutive_law_pt

ConstitutiveLaw * Constitutive_law_pt

Constitutive law used to determine the mesh deformation.

Definition: refineable_two_layer_interface.cc:332

We loop over the bulk elements in the lower fluid and pass them pointers to the Reynolds and Womersley numbers, and $Re\, St$ , the product of the Reynolds number and the inverse of the Froude number, , the direction of gravity, , the constitutive law and the global time object, created when we called Problem::add_time_stepper_pt(...) above. Note that we do not assign pointers for the viscosity and density ratios, $R_\mu$ and $R_\rho$ , since these take the default value in the lower fluid.

 // Complete the problem setup to make the elements fully functional
 // ----------------------------------------------------------------
 
 // Compute number of bulk elements in lower/upper fluids
 const unsigned n_lower = n_x*n_y1;
 const unsigned n_upper = n_x*n_y2;
 
 // Loop over bulk elements in lower fluid
 for(unsigned e=0;e<n_lower;e++)
  {
   // Upcast from GeneralisedElement to the present element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(Bulk_mesh_pt->element_pt(e));
 
   // Set the Reynolds number
   el_pt->re_pt() = &Global_Physical_Variables::Re;
 
   // Set the Womersley number
   el_pt->re_st_pt() = &Global_Physical_Variables::ReSt;
 
   // Set the product of the Reynolds number and the inverse of the
   // Froude number
   el_pt->re_invfr_pt() = &Global_Physical_Variables::ReInvFr;
 
   // Set the direction of gravity
   el_pt->g_pt() = &Global_Physical_Variables::G;
 
   // Set the constitutive law
   el_pt->constitutive_law_pt() = Constitutive_law_pt;
 
  } // End of loop over bulk elements in lower fluid

We then do the same for the bulk elements in the upper fluid, and this time we do assign pointers for the viscosity and density ratios.

 // Loop over bulk elements in upper fluid
 for(unsigned e=n_lower;e<(n_lower+n_upper);e++)
  {
   // Upcast from GeneralisedElement to the present element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(Bulk_mesh_pt->element_pt(e));
 
   // Set the Reynolds number
   el_pt->re_pt() = &Global_Physical_Variables::Re;
 
   // Set the Womersley number
   el_pt->re_st_pt() = &Global_Physical_Variables::ReSt;
 
   // Set the product of the Reynolds number and the inverse of the
   // Froude number
   el_pt->re_invfr_pt() = &Global_Physical_Variables::ReInvFr;
 
   // Set the viscosity ratio
   el_pt->viscosity_ratio_pt() = &Global_Physical_Variables::Viscosity_Ratio;
 
   // Set the density ratio
   el_pt->density_ratio_pt() = &Global_Physical_Variables::Density_Ratio;
 
   // Set the direction of gravity
   el_pt->g_pt() = &Global_Physical_Variables::G;
 
   // Set the constitutive law
   el_pt->constitutive_law_pt() = Constitutive_law_pt;
 
  } // End of loop over bulk elements in upper fluid

We then pin one pressure degree of freedom.

// Set the pressure in the first element at 'node' 0 to 0.0

fix_pressure(0,0,0.0);

At this point we set up the boundary conditions.

// Apply the boundary conditions

set_boundary_conditions();

Finally, we set up the equation numbering scheme.

 // Set up equation numbering scheme
 cout << "Number of equations: " << assign_eqn_numbers() << std::endl;
 
} // End of constructor

Initial conditions

The set_initial_conditions() function is identical to that in the previous example.

Boundary conditions

The set_boundary_conditions() function is very similar to that in the previous example.

Actions before adaptation

The mesh adaptation is driven by the error estimates in the bulk elements and only performed for that mesh. The interface elements must therefore be removed before adaptation. We do this by calling the function delete_interface_elements(), and then rebuilding the Problem's global mesh.

//==start_of_actions_before_adapt=========================================
/// Strip off the interface elements before adapting the bulk mesh
//========================================================================
template<class ELEMENT, class TIMESTEPPER>
void InterfaceProblem<ELEMENT,TIMESTEPPER>::actions_before_adapt()
{
 // Delete the interface elements and wipe the surface mesh
 delete_interface_elements();
 
 // Rebuild the Problem's global mesh from its various sub-meshes
 rebuild_global_mesh();
 
} // End of actions_before_adapt

Actions after adapt

After the bulk mesh has been adapted we must create new interface elements and rebuild the problem's global mesh. Any newly-created boundary nodes will automatically have the appropriate boundary conditions applied; however, we must remember to pin the horizontal displacement of all nodes throughout the bulk of the domain.

//==start_of_actions_after_adapt==========================================
/// Rebuild the mesh of interface elements after adapting the bulk mesh
//========================================================================
template<class ELEMENT, class TIMESTEPPER>
void InterfaceProblem<ELEMENT,TIMESTEPPER>::actions_after_adapt()
{
 // Create the interface elements
 this->create_interface_elements();
 
 // Rebuild the Problem's global mesh from its various sub-meshes
 rebuild_global_mesh();
 
 // Pin horizontal displacement of all nodes
 const unsigned n_node = Bulk_mesh_pt->nnode();
 for(unsigned n=0;n<n_node;n++) { Bulk_mesh_pt->node_pt(n)->pin_position(0); }

To ensure that precisely one fluid pressure degree of freedom is pinned, we unpin all pressure degrees of freedom, pin any redundant nodal pressures which have arisen following mesh adaptation and call fix_pressure(...). We also pin any redundant solid pressures before re-setting the boundary conditions.

 // Unpin all fluid pressure dofs
 RefineableNavierStokesEquations<2>::
  unpin_all_pressure_dofs(Bulk_mesh_pt->element_pt());
 
 // Pin redudant fluid pressure dofs
 RefineableNavierStokesEquations<2>::
  pin_redundant_nodal_pressures(Bulk_mesh_pt->element_pt());
 
 // Now set the pressure in the first element at 'node' 0 to 0.0
 fix_pressure(0,0,0.0);
 
 // Pin the redundant solid pressures (if any)
 PVDEquationsBase<2>::pin_redundant_nodal_solid_pressures(
  Bulk_mesh_pt->element_pt());
 
 // Reset the boundary conditions
 set_boundary_conditions();
 
} // End of actions_after_adapt

Create interface elements

This function is used to ‘attach’ interface elements to the upper face of those bulk elements in the lower fluid which are adjacent to the interface. Firstly, we loop over all bulk elements (in either fluid) which are adjacent to the interface.

//==start_of_create_interface_elements====================================
/// Create interface elements between the two fluids in the mesh
/// pointed to by Bulk_mesh_pt and add the elements to the Mesh object
/// pointed to by Surface_mesh_pt.
//========================================================================
template <class ELEMENT, class TIMESTEPPER>
void InterfaceProblem<ELEMENT,TIMESTEPPER>::create_interface_elements()
{
 // Determine number of bulk elements adjacent to interface (boundary 4)
 const unsigned n_element = this->Bulk_mesh_pt->nboundary_element(4);
 
 // Loop over those elements adjacent to the interface
 for(unsigned e=0;e<n_element;e++)
  {
   // Get pointer to the bulk element that is adjacent to the interface
   ELEMENT* bulk_elem_pt = dynamic_cast<ELEMENT*>(
    this->Bulk_mesh_pt->boundary_element_pt(4,e));

In order to determine whether the bulk element we are currently looking at is in the upper or lower fluid, we check to see whether that element's viscosity_ratio_pt is pointing to the address of Global_Physical_Variables::Viscosity_Ratio. If it is, then that bulk element is in the upper fluid, and we ignore it. Otherwise, we determine the face of the bulk element that corresponds to the interface and create an interface element on that face. The newly-created element is then added to the surface mesh.

   // We only want to attach interface elements to the bulk elements
   // which are BELOW the interface, and so we filter out those above by
   // referring to the viscosity_ratio_pt
   if(bulk_elem_pt->viscosity_ratio_pt()
      !=&Global_Physical_Variables::Viscosity_Ratio)
    {
     // Find index of the face of element e that corresponds to the interface
     const int face_index = this->Bulk_mesh_pt->face_index_at_boundary(4,e);
     
     // Create the interface element
     FiniteElement* interface_element_element_pt =
      new ElasticLineFluidInterfaceElement<ELEMENT>(bulk_elem_pt,face_index);
 
     // Add the interface element to the surface mesh
     this->Surface_mesh_pt->add_element_pt(interface_element_element_pt);
    }

Finally, we pass the Strouhal and Capillary numbers to the interface elements.

 // Complete the setup to make the elements fully functional
 // --------------------------------------------------------
 
 // Determine number of 1D interface elements in mesh
 const unsigned n_interface_element = this->Surface_mesh_pt->nelement();
 
 // Loop over the interface elements
 for(unsigned e=0;e<n_interface_element;e++)
  {
   // Upcast from GeneralisedElement to the present element
   ElasticLineFluidInterfaceElement<ELEMENT>* el_pt = 
    dynamic_cast<ElasticLineFluidInterfaceElement<ELEMENT>*>
    (Surface_mesh_pt->element_pt(e));
 
   // Set the Strouhal number
   el_pt->st_pt() = &Global_Physical_Variables::St;
 
   // Set the Capillary number
   el_pt->ca_pt() = &Global_Physical_Variables::Ca;
 
  } // End of loop over interface elements
 
} // End of create_interface_elements

Delete interface elements

This function loops over all the interface elements (i.e. those in the surface mesh) and deletes them and their storage.

//==start_of_delete_interface_elements====================================
/// Delete the interface elements and wipe the surface mesh
//========================================================================
template <class ELEMENT, class TIMESTEPPER>
void InterfaceProblem<ELEMENT,TIMESTEPPER>::delete_interface_elements()
{
 // Determine number of interface elements
 const unsigned n_interface_element = Surface_mesh_pt->nelement();
 
 // Loop over interface elements and delete
 for(unsigned e=0;e<n_interface_element;e++)
  {
   delete Surface_mesh_pt->element_pt(e);
  }
 
 // Wipe the mesh
 Surface_mesh_pt->flush_element_and_node_storage();
 
} // End of delete_interface_elements

Prescribing the initial free surface position

At the beginning of the simulation the interface is deformed by a prescribed function (11), implemented in the function deform_free_surface(...), which cycles through the bulk mesh's Nodes and modifies their positions such that the nodes on the free surface follow the prescribed interface shape and the bulk nodes retain their fractional position between the solid boundaries and the (now deformed) interface.

//==start_of_deform_free_surface==========================================
/// Deform the mesh/free surface to a prescribed function
//========================================================================
template <class ELEMENT, class TIMESTEPPER>
void InterfaceProblem<ELEMENT,TIMESTEPPER>::
deform_free_surface(const double &epsilon,const unsigned &n_periods)
{
 // Determine number of nodes in the "bulk" mesh
 const unsigned n_node = Bulk_mesh_pt->nnode();
 
 // Loop over all nodes in mesh
 for(unsigned n=0;n<n_node;n++)
  {
   // Determine eulerian position of node
   const double current_x_pos = Bulk_mesh_pt->node_pt(n)->x(0);
   const double current_y_pos = Bulk_mesh_pt->node_pt(n)->x(1);
   
   // Determine new vertical position of node
   const double new_y_pos = current_y_pos
    + (1.0-fabs(1.0-current_y_pos))*epsilon
    *(cos(2.0*n_periods*MathematicalConstants::Pi*current_x_pos/Lx));
   
   // Set new position
   Bulk_mesh_pt->node_pt(n)->x(1) = new_y_pos;
  }
} // End of deform_free_surface

Post-processing

This function is identical to that in the previous example.

The timestepping loop

The function unsteady_run(...) is used to perform the timestepping procedure, and is very similar to that in the previous example. The only changes arise due to this problem being solved with spatial adaptivity. We start by deforming the interface in the manner specified by equation (11).

//==start_of_unsteady_run=================================================
/// Perform run up to specified time t_max with given timestep dt
//========================================================================
template <class ELEMENT, class TIMESTEPPER>
void InterfaceProblem<ELEMENT,TIMESTEPPER>::
unsteady_run(const double &t_max, const double &dt)
{
 
 // Set value of epsilon
 const double epsilon = 0.1;
 
 // Set number of periods for cosine term
 const unsigned n_periods = 1;
 
 // Deform the mesh/free surface
 deform_free_surface(epsilon,n_periods);

We then create a DocInfo object to store the output directory and the label for the output files.

 // Initialise DocInfo object
 DocInfo doc_info;
 
 // Set output directory
 doc_info.set_directory("RESLT");
 
 // Initialise counter for solutions
 doc_info.number()=0;

Next we open and initialise the trace file.

 // Open trace file
 char filename[100];   
 sprintf(filename,"%s/trace.dat",doc_info.directory().c_str());
 Trace_file.open(filename);
 
 // Initialise trace file
 Trace_file << "time, interface height" << std::endl;

Before using any of oomph-lib's timestepping functions, the timestep must be passed to the problem's timestepping routines by calling the function Problem::initialise_dt(...) which sets the weights for all timesteppers in the problem. Next we assign the initial conditions by calling Problem::set_initial_condition(), which was discussed above.

 // Initialise timestep
 initialise_dt(dt);
 
 // Set initial condition
 set_initial_condition();

We limit number of spatial adaptations per timestep to two and refine the problem uniformly twice, before documenting the initial conditions.

 // Maximum number of spatial adaptations per timestep
 unsigned max_adapt = 2;
 
 // Call refine_uniformly twice
 for(unsigned i=0;i<2;i++) { refine_uniformly(); }
 
 // Doc initial solution
 doc_solution(doc_info);
 
 // Increment counter for solutions
 doc_info.number()++;

Finally, we determine the number of timesteps to be performed and perform the actual timestepping loop. For each timestep the function unsteady_newton_solve(dt,max_adapt,first_timestep) is called and the solution documented. The boolean flag first_timestep is used to instruct the code to re-assign the initial conditions after every mesh adaptation. After the first timestep, the maximum number of adaptations for all timesteps is reset to one. We refer to another example for a discussion of why this is recommended.

 // Determine number of timesteps
 const unsigned n_timestep = unsigned(t_max/dt);
 
 // Are we on the first timestep? At this point, yes!
 bool first_timestep = true;
 
 // Timestepping loop
 for(unsigned t=1;t<=n_timestep;t++)
  {
   // Output current timestep to screen
   cout << "\nTimestep " << t << " of " << n_timestep << std::endl;
   
   // Take one fixed timestep with spatial adaptivity
   unsteady_newton_solve(dt,max_adapt,first_timestep);
 
   // No longer on first timestep, so set first_timestep flag to false
   first_timestep = false; 
 
   // Reset maximum number of adaptations for all future timesteps
   max_adapt = 1;
 
   // Doc solution
   doc_solution(doc_info);
 
   // Increment counter for solutions 
   doc_info.number()++;
 
  } // End of timestepping loop
 
} // End of unsteady_run

Comments

Since the problem discussed in this example has the fluid velocity prescribed along the entire domain boundary, the fluid pressure is only determined up to an arbitrary constant and hence we fix the pressure at a single point in the domain. However, it is worth noting that in the case of Crouzeix–Raviart elements being used in a problem with spatial adaptivity the notion of a fixed pressure is slightly subtle. In this example we fix the first pressure value of the first element in the mesh to zero, which in the case of Crouzeix–Raviart elements means that we fix the average value of the pressure to zero in this element. Were this element to be refined, however, we would then be imposing a zero pressure elsewhere in the domain, causing the entire pressure field to ‘jump’ from one timestep to the next. Since the problem is incompressible this would not affect the computed velocity fields, but could lead to some confusion when studying the time evolution of the pressure field.

Exercises

In the single-layer example we chose to discretise the problem using Crouzeix–Raviart elements, but we could also have chosen to use Taylor–Hood elements. Why can we not use Taylor–Hood elements to solve this two-layer problem?
What happens if we do not call setup_boundary_element_info() in the mesh constructor? Why is this?

Source files for this tutorial

The source files for this tutorial are located in the directory: demo_drivers/navier_stokes/two_layer_interface/
The driver code is: demo_drivers/navier_stokes/two_layer_interface/elastic_two_layer_interface.cc

PDF file

A pdf version of this document is available.