In this example we study the compression of a 2D circular disk, loaded by an external pressure. We also demonstrate:

how to "upgrade" a Mesh to a SolidMesh
why it is necessary to use "undeformed MacroElements" to ensure that the numerical results converge to the correct solution under mesh refinement if the domain has curvilinear boundaries.
how to switch between different constitutive equations
how to incorporate isotropic growth into the model

We validate the numerical results by comparing them against the analytical solution of the equations of linear elasticity which are valid for small deflections.

The problem

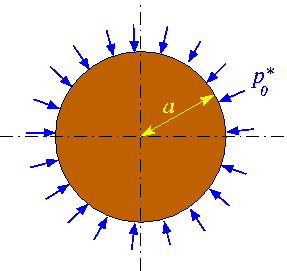
The figure below shows a sketch of the basic problem: A 2D circular disk of radius is loaded by a uniform pressure . We wish to compute the disk's deformation for a variety of constitutive equations.

Sketch of the problem.

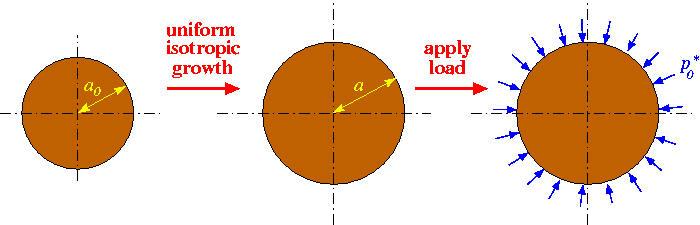
The next sketch shows a variant of the problem: We assume that the material undergoes isotropic growth (e.g. via a biological growth process or thermal expansion, say) with a constant growth factor $\Gamma$ . We refer to the the document "Solid mechanics: Theory and implementation" for a detailed discussion of the theory of isotropic growth. Briefly, the growth factor defines the relative increase in the volume of an infinitesimal material element, relative to its volume in the stress-free reference configuration. If the growth factor is spatially uniform, isotropic growth leads to a uniform expansion of the material. For a circular disk, uniform growth increases the disk's radius from to $a = a_0 \sqrt{\Gamma}$ without inducing any internal stresses. This uniformly expanded disk may then be regarded as the stress-free reference configuration upon which the external pressure acts.

Sketch of the problem.

Results

The animation shows the disk's deformation when subjected to uniform growth of $\Gamma = 1.1$ and loaded by a pressure that ranges from negative to positive values. All lengths were scaled on the disks initial radius (i.e. its radius in the absence of growth and without any external load).

Deformation of the uniformly grown disk when subjected to an external pressure.

The figure below illustrates the disk's load-displacement characteristics by plotting the disk's non-dimensional radius as function of the non-dimensional pressure, $p_0 = p_0^*/{\cal S}$ , where ${\cal S}$ is the characteristic stiffness of the material, for a variety of constitutive equations.

Load displacement characteristics for various constitutive equations.

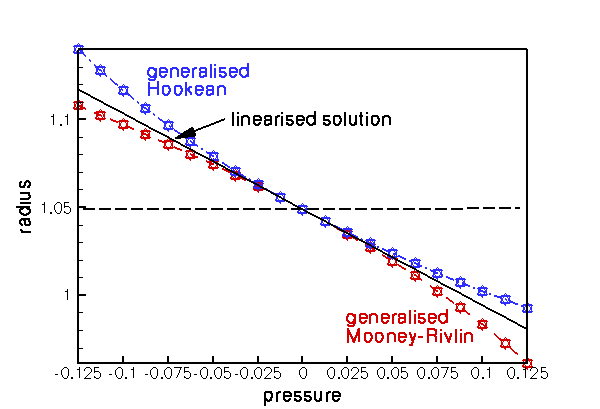
Generalised Hooke's law

The blue, dash-dotted line corresponds to oomph-lib's generalisation of Hooke's law (with Young's modulus and Poisson ratio $\nu$ ) in which the dimensionless second Piola Kirchhoff stress tensor (non-dimensionalised with the material's Young's modulus , so that ${\cal S} = E$ ) is given by

$\sigma^{ij} = \frac{1}{2(1+\nu)} \left( G^{ik} G^{jl} + G^{il} G^{jk} + \frac{2\nu}{1-2\nu} G^{ij} G^{kl} \right) \gamma_{kl}.$

Here $\gamma_{ij}= 1/2 (G_{ij}-g_{ij})$ is Green's strain tensor, formed from the difference between the deformed and undeformed metric tensors, $G_{ij}$ and $g_{ij}$ , respectively. The three different markers identify the results obtained with the two forms of the principle of virtual displacement, employing the displacement formulation (squares), and a pressure/displacement formulation with a continuous (delta) and a discontinuous (nabla) pressure interpolation.

For zero pressure the disk's non-dimensional radius is equal to the uniformly grown radius $\sqrt{\Gamma} = 1.0488.$ For small pressures the load-displacement curve follows the linear approximation

$r = \sqrt{\Gamma} \big( 1-p_0 (1+\nu)(1-2\nu) \big).$

We note that the generalised Hooke's law leads to strain softening behaviour under compression (the pressure required to reduce the disk's radius to a given value increases more rapidly than predicted by the linear approximation) whereas under expansion (for negative external pressures) the behaviour is strain softening.

Generalised Mooney-Rivlin law

The red, dashed line illustrates the behaviour when Fung & Tong's generalisation of the Mooney-Rivlin law (with Young's modulus, , Poisson ratio $\nu$ and Mooney-Rivlin parameter ) is used as the constitutive equation. For this constitutive law, the non-dimensional strain energy function $W = W^*/{\cal S}$ , where the characteristic stress is given by Young's modulus, i.e. ${\cal S} =E$ , is given by

$W = \frac{1}{2} (I_1-3) + (G-C_1)(I_2-3) + (C_1-2G)(I_3-1) + (I_3-1)^2 \ \frac{G(1-\nu)}{2(1-2\nu)} \ ,$

where

$G = \frac{E}{2(1+\nu)}$

is the shear modulus, and and are the three invariants of Green's strain tensor. See "Solid mechanics: Theory and implementation" for a detailed discussion of strain energy functions. The figure shows that for small deflections, the disk's behaviour is again well approximated by linear elasticity. However, in the large-displacement regime the Mooney-Rivlin is strain hardening under extension and softening under compression when compared to the linear elastic behaviour.

Global parameters and functions

As usual we define the global problem parameters in a namespace. We provide pointers to the constitutive equations and strain energy functions to be explored, and define the associated constitutive parameters.

//============namespace_for_problem_parameters=====================
/// Global variables
//=================================================================
namespace Global_Physical_Variables
{
 /// Pointer to strain energy function
 StrainEnergyFunction* Strain_energy_function_pt;
 
 /// Pointer to constitutive law
 ConstitutiveLaw* Constitutive_law_pt;
 
 /// Elastic modulus
 double E=1.0; 
 
 /// Poisson's ratio
 double Nu=0.3;
 
 /// "Mooney Rivlin" coefficient for generalised Mooney Rivlin law
 double C1=1.3;

Next we define the pressure load, using the general interface defined in the SolidTractionElement class. The arguments of the function reflect that the load on a solid may be a function of the Lagrangian and Eulerian coordinates, and the external unit normal on the solid. Here we apply a spatially constant external pressure of magnitude P which acts in the direction of the negative outer unit normal on the solid.

 
 /// Uniform pressure
 double P = 0.0;
 
 /// Constant pressure load
 void constant_pressure(const Vector<double> &xi,const Vector<double> &x,
                        const Vector<double> &n, Vector<double> &traction)
 {
  unsigned dim = traction.size();
  for(unsigned i=0;i<dim;i++)
   {
    traction[i] = -P*n[i];
   }
 } // end of pressure load

Finally, we define the growth function and impose a spatially uniform expansion that (in the absence of any external load) would increase the disk's volume by 10%.

 
 
 /// Uniform volumetric expansion
 double Uniform_gamma=1.1;
 
 /// Growth function
 void growth_function(const Vector<double>& xi, double& gamma)
 {
  gamma = Uniform_gamma;
 }
 
} // end namespace

The driver code

The driver code is very short: We store the command line arguments (as usual, we use a non-zero number of command line arguments as an indication that the code is run in self-test mode and reduce the number of steps performed in the parameter study) and create a strain-energy-based constitutive equation: Fung & Tong's generalisation of the Mooney-Rivlin law.

//=====start_of_main====================================================
/// Driver code for disk-compression
//======================================================================
int main(int argc, char* argv[])
{
 
 // Store command line arguments
 CommandLineArgs::setup(argc,argv);
  
 // Define a strain energy function: Generalised Mooney Rivlin
 Global_Physical_Variables::Strain_energy_function_pt = 
  new GeneralisedMooneyRivlin(&Global_Physical_Variables::Nu,
                              &Global_Physical_Variables::C1,
                              &Global_Physical_Variables::E);
 
 // Define a constitutive law (based on strain energy function)
 Global_Physical_Variables::Constitutive_law_pt = 
  new IsotropicStrainEnergyFunctionConstitutiveLaw(
   Global_Physical_Variables::Strain_energy_function_pt);

We build a problem object, using the displacement-based RefineableQPVDElements to discretise the domain, and perform a parameter study, exploring the disk's deformation for a range of external pressures.

 
 // Case 0: No pressure, generalised Mooney Rivlin
 //-----------------------------------------------
 {
    //Set up the problem
  StaticDiskCompressionProblem<RefineableQPVDElement<2,3> > problem;
  
  cout << "gen. M.R.: RefineableQPVDElement<2,3>" << std::endl;
  
  //Run the simulation
  problem.parameter_study(0);
  
 } // done case 0

We repeat the exercise with elements from the RefineableQPVDElementWithContinuousPressure family which discretise the principle of virtual displacements (PVD) in the pressure/displacement formulation, using continuous pressures (Q2Q1; Taylor Hood).

 
 
 // Case 1: Continuous pressure formulation with generalised Mooney Rivlin
 //------------------------------------------------------------------------
 {
  //Set up the problem
  StaticDiskCompressionProblem<
   RefineableQPVDElementWithContinuousPressure<2> > problem;
  
  cout << "gen. M.R.: RefineableQPVDElementWithContinuousPressure<2> " 
       << std::endl;
  
  //Run the simulation
  problem.parameter_study(1);
 
 }  // done case 1

The next computation employs RefineableQPVDElementWithPressure elements in which the pressure is interpolated by piecewise linear but globally discontinuous basis functions (Q2Q-1; Crouzeiux-Raviart).

 
 
 
 // Case 2: Discontinuous pressure formulation with generalised Mooney Rivlin
 //--------------------------------------------------------------------------
 {
  //Set up the problem
  StaticDiskCompressionProblem<RefineableQPVDElementWithPressure<2> > 
   problem;
  
  cout << "gen. M.R.: RefineableQPVDElementWithPressure<2>" << std::endl;
  
  //Run the simulation
  problem.parameter_study(2);
  
 }  // done case 2

Next, we change the constitutive equation to oomph-lib's generalised Hooke's law,

 
 
 // Change the consitutive law: Delete the old one
 delete Global_Physical_Variables::Constitutive_law_pt;
 
 // Create oomph-lib's generalised Hooke's law constitutive equation
 Global_Physical_Variables::Constitutive_law_pt = 
  new GeneralisedHookean(&Global_Physical_Variables::Nu,
                         &Global_Physical_Variables::E);

before repeating the parameter studies with the same three element types:

 
 // Case 3: No pressure, generalised Hooke's law
 //----------------------------------------------
 {
  //Set up the problem
  StaticDiskCompressionProblem<RefineableQPVDElement<2,3> > problem;
  
  cout << "gen. Hooke: RefineableQPVDElement<2,3> " << std::endl;
  
  //Run the simulation
  problem.parameter_study(3);  
 
 }  // done case 3
 
 // Case 4: Continuous pressure formulation with generalised Hooke's law
 //---------------------------------------------------------------------
 {
  
  //Set up the problem
  StaticDiskCompressionProblem<
   RefineableQPVDElementWithContinuousPressure<2> > problem;
  
  cout << "gen. Hooke: RefineableQPVDElementWithContinuousPressure<2> " 
       << std::endl;
  
  //Run the simulation
  problem.parameter_study(4);
  
 }  // done case 4
 
 
 // Case 5:  Discontinous pressure formulation with generalised Hooke's law
 //------------------------------------------------------------------------
 {
  
  //Set up the problem
  StaticDiskCompressionProblem<RefineableQPVDElementWithPressure<2> > problem;
  
  cout << "gen. Hooke: RefineableQPVDElementWithPressure<2> " << std::endl;
  
  //Run the simulation
  problem.parameter_study(5);
    
 }  // done case 5
 
 // Clean up 
 delete Global_Physical_Variables::Constitutive_law_pt;
 Global_Physical_Variables::Constitutive_law_pt=0;
 
} // end of main

The mesh

We formulate the problem in cartesian coordinates (ignoring the problem's axisymmetry) but discretise only one quarter of the domain, applying appropriate symmetry conditions along the x and y axes. The computational domain may be discretised with the RefineableQuarterCircleSectorMesh that we already used in many previous examples. To use the mesh in this solid mechanics problem we must first "upgrade" it to a SolidMesh. This is easily done by multiple inheritance:

//==========start_mesh=================================================
/// Elastic quarter circle sector mesh with functionality to
/// attach traction elements to the curved surface. We "upgrade"
/// the RefineableQuarterCircleSectorMesh to become an
/// SolidMesh and equate the Eulerian and Lagrangian coordinates,
/// thus making the domain represented by the mesh the stress-free 
/// configuration. 
/// \n\n
/// The member function \c make_traction_element_mesh() creates
/// a separate mesh of SolidTractionElements that are attached to the
/// mesh's curved boundary (boundary 1). 
//=====================================================================
template <class ELEMENT>
class ElasticRefineableQuarterCircleSectorMesh :
 public virtual RefineableQuarterCircleSectorMesh<ELEMENT>,
 public virtual SolidMesh
{

The constructor calls the constructor of the underlying RefineableQuarterCircleSectorMesh and sets the Lagrangian coordinates of the nodes to their current Eulerian positions, making the initial configuration stress-free.

 
 
public:
 
 /// Constructor: Build mesh and copy Eulerian coords to Lagrangian
 /// ones so that the initial configuration is the stress-free one.
 ElasticRefineableQuarterCircleSectorMesh<ELEMENT>(GeomObject* wall_pt,
                                         const double& xi_lo,
                                         const double& fract_mid,
                                         const double& xi_hi,
                                         TimeStepper* time_stepper_pt=
                                         &Mesh::Default_TimeStepper) :
  RefineableQuarterCircleSectorMesh<ELEMENT>(wall_pt,xi_lo,fract_mid,xi_hi,
                                             time_stepper_pt)
  {
   /// Make the current configuration the undeformed one by
   /// setting the nodal Lagrangian coordinates to their current
   /// Eulerian ones
   set_lagrangian_nodal_coordinates();
  }

We also provide a helper function that creates a mesh of SolidTractionElements which are attached to the curved domain boundary (boundary 1). These elements will be used to apply the external pressure load.

 
 
 /// Function to create mesh made of traction elements
 void make_traction_element_mesh(SolidMesh*& traction_mesh_pt)
  {
 
   // Make new mesh
   traction_mesh_pt = new SolidMesh;
 
   // Loop over all elements on boundary 1:
   unsigned b=1;
   unsigned n_element = this->nboundary_element(b);
   for (unsigned e=0;e<n_element;e++)
    {
     // The element itself:
     FiniteElement* fe_pt = this->boundary_element_pt(b,e);
     
     // Find the index of the face of element e along boundary b
     int face_index = this->face_index_at_boundary(b,e);
     
     // Create new element
     traction_mesh_pt->add_element_pt(new SolidTractionElement<ELEMENT>
                                      (fe_pt,face_index));
    }
  }
 
};

The Problem class

The definition of the Problem class is very straightforward. In addition to the constructor and the (empty) actions_before_newton_solve() and actions_after_newton_solve() functions, we provide the function parameter_study(...) which performs a parameter study, computing the disk's deformation for a range of external pressures. The member data includes pointers to the mesh of "bulk" solid elements, and the mesh of SolidTractionElements that apply the pressure load. The trace file is used to document the disk's load-displacement characteristics by plotting the radial displacement of the nodes on the curvilinear boundary, pointers to which are stored in the vector Trace_node_pt.

 
 
//====================================================================== 
/// Uniform compression of a circular disk in a state of plane strain,
/// subject to uniform growth. 
//====================================================================== 
template<class ELEMENT>
class StaticDiskCompressionProblem : public Problem
{
 
public:
 
 /// Constructor:
 StaticDiskCompressionProblem();
 
 /// Run simulation: Pass case number to label output files
 void parameter_study(const unsigned& case_number);
 
 /// Doc the solution
 void doc_solution(DocInfo& doc_info);
 
 /// Update function (empty)
 void actions_after_newton_solve() {}
 
 /// Update function (empty)
 void actions_before_newton_solve() {}
 
private:
 
 /// Trace file
 ofstream Trace_file;
 
 /// Vector of pointers to nodes whose position we're tracing
 Vector<Node*> Trace_node_pt;
 
 /// Pointer to solid mesh
 ElasticRefineableQuarterCircleSectorMesh<ELEMENT>* Solid_mesh_pt;
 
 /// Pointer to mesh of traction elements
 SolidMesh* Traction_mesh_pt;
 
};

The Constructor

We start by constructing the mesh of "bulk" SolidElements, using the Ellipse object to specify the shape of the curvilinear domain boundary.

 
//====================================================================== 
/// Constructor: 
//====================================================================== 
template<class ELEMENT>
StaticDiskCompressionProblem<ELEMENT>::StaticDiskCompressionProblem() 
{
 // Build the geometric object that describes the curvilinear
 // boundary of the quarter circle domain
 Ellipse* curved_boundary_pt = new Ellipse(1.0,1.0);
 
 // The curved boundary of the mesh is defined by the geometric object
 // What follows are the start and end coordinates on the geometric object:
 double xi_lo=0.0;
 double xi_hi=2.0*atan(1.0);
 
 // Fraction along geometric object at which the radial dividing line
 // is placed
 double fract_mid=0.5;
 
 //Now create the mesh using the geometric object
 Solid_mesh_pt = new ElasticRefineableQuarterCircleSectorMesh<ELEMENT>(
  curved_boundary_pt,xi_lo,fract_mid,xi_hi);

Next we choose the nodes on the curvilinear domain boundary (boundary 1) as the nodes whose displacement we document in the trace file.

 
 // Setup trace nodes as the nodes on boundary  1 (=curved boundary) 
 // in the original mesh.
 unsigned n_boundary_node = Solid_mesh_pt->nboundary_node(1);
 Trace_node_pt.resize(n_boundary_node);
 for(unsigned j=0;j<n_boundary_node;j++)
  {Trace_node_pt[j]=Solid_mesh_pt->boundary_node_pt(1,j);}

The QuarterCircleSectorMesh that forms the basis of the "bulk" mesh contains only three elements – not enough to expect the solution to be accurate. Therefore we apply one round of uniform mesh refinement before attaching the SolidTractionElements to the mesh boundary 1, using the function make_traction_element_mesh() in the ElasticRefineableQuarterCircleSectorMesh.

 
 // Refine the mesh uniformly
 Solid_mesh_pt->refine_uniformly();
 
 // Now construct the traction element mesh
 Solid_mesh_pt->make_traction_element_mesh(Traction_mesh_pt);

We add both meshes to the Problem and build a combined global mesh:

 
 // Solid mesh is first sub-mesh
 add_sub_mesh(Solid_mesh_pt);
 
 // Traction mesh is second sub-mesh
 add_sub_mesh(Traction_mesh_pt);
 
 // Build combined "global" mesh
 build_global_mesh();

Symmetry boundary conditions along the horizontal and vertical symmetry lines require that the nodes' vertical position is pinned along boundary 0, while their horizontal position is pinned along boundary 2.

 
 
 // Pin the left edge in the horizontal direction
 unsigned n_side = mesh_pt()->nboundary_node(2);
 for(unsigned i=0;i<n_side;i++)
  {Solid_mesh_pt->boundary_node_pt(2,i)->pin_position(0);}
 
 // Pin the bottom in the vertical direction
 unsigned n_bottom = mesh_pt()->nboundary_node(0);
 for(unsigned i=0;i<n_bottom;i++)
  {Solid_mesh_pt->boundary_node_pt(0,i)->pin_position(1);}

Since we are using refineable solid elements, we pin any "redundant" pressure degrees of freedom in the "bulk" solid mesh (see the exercises in another tutorial for a more detailed discussion of this issue).

 
 // Pin the redundant solid pressures (if any)
 PVDEquationsBase<2>::pin_redundant_nodal_solid_pressures(
  Solid_mesh_pt->element_pt());

Next, we complete the build of the elements in the "bulk" solid mesh by passing the pointer to the constitutive equation and the pointer to the isotropic-growth function to the elements:

 
 //Complete the build process for elements in "bulk" solid mesh
 unsigned n_element =Solid_mesh_pt->nelement();
 for(unsigned i=0;i<n_element;i++)
  {
   //Cast to a solid element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(Solid_mesh_pt->element_pt(i));
   
   // Set the constitutive law
   el_pt->constitutive_law_pt() =
    Global_Physical_Variables::Constitutive_law_pt;
   
   // Set the isotropic growth function pointer
   el_pt->isotropic_growth_fct_pt()=Global_Physical_Variables::growth_function;
  }

We repeat this exercise for the SolidTractionElements which must be given a pointer to the function that applies the pressure load

 
 // Complete build process for SolidTractionElements
 n_element=Traction_mesh_pt->nelement();
 for(unsigned i=0;i<n_element;i++)
  {
   //Cast to a solid traction element
   SolidTractionElement<ELEMENT> *el_pt = 
    dynamic_cast<SolidTractionElement<ELEMENT>*>
    (Traction_mesh_pt->element_pt(i));
 
   //Set the traction function
   el_pt->traction_fct_pt() = Global_Physical_Variables::constant_pressure;
  }

Finally, we set up the equation numbering scheme and report the number of unknowns.

 
 //Set up equation numbering scheme
 cout << "Number of equations: " <<  assign_eqn_numbers() << std::endl; 
}

Post-processing

The post-processing function outputs the shape of the deformed disk. We use the trace file to record how the disk's volume (area) and the radii of the control nodes on the curvilinear domain boundary vary with the applied pressure. To facilitate the validation of the results against the analytical solution, we also add the radius predicted by the linear theory to the trace file.

 
 
//==================================================================
/// Doc the solution
//==================================================================
template<class ELEMENT>
void StaticDiskCompressionProblem<ELEMENT>::doc_solution(DocInfo& doc_info)
{
 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned npts = 5; 
 
 // Output shape of deformed body
 sprintf(filename,"%s/soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 Solid_mesh_pt->output(some_file,npts);
 some_file.close();
 
 //Find number of solid elements
 unsigned nelement = Solid_mesh_pt->nelement();
 
 // Work out volume
 double volume = 0.0;
 for(unsigned e=0;e<nelement;e++) 
  {volume+= Solid_mesh_pt->finite_element_pt(e)->size();}
 
 // Exact outer radius for linear elasticity
 double nu=Global_Physical_Variables::Nu;
 double exact_r=sqrt(Global_Physical_Variables::Uniform_gamma)*
  (1.0-Global_Physical_Variables::P/Global_Physical_Variables::E
   *((1.0+nu)*(1.0-2.0*nu)));
 
 
 // Write trace file: Problem parameters
 Trace_file << Global_Physical_Variables::P  << " " 
            << Global_Physical_Variables::Uniform_gamma << " " 
            << volume << " " 
            << exact_r << " ";
   
 // Write radii of trace nodes
 unsigned ntrace_node=Trace_node_pt.size();
 for (unsigned j=0;j<ntrace_node;j++)
  {
   Trace_file << sqrt(pow(Trace_node_pt[j]->x(0),2)+
                      pow(Trace_node_pt[j]->x(1),2)) << " ";
  }
 Trace_file << std::endl;
 
} // end of doc_solution

Performing the parameter study

The function parameter_study(...) computes the disk's deformation for a range of external pressures and outputs the results. The output directory is labelled by the unsigned function argument. This ensures that parameter studies performed with different constitutive equations are written into different directories.

 
 
//==================================================================
/// Run the paramter study
//==================================================================
template<class ELEMENT>
void StaticDiskCompressionProblem<ELEMENT>::parameter_study(
 const unsigned& case_number)
{
 // Output
 DocInfo doc_info;
 
 char dirname[100];
 sprintf(dirname,"RESLT%i",case_number);
 
 // Set output directory
 doc_info.set_directory(dirname);
 
 // Step number
 doc_info.number()=0;
 
 // Open trace file
 char filename[100];   
 sprintf(filename,"%s/trace.dat",doc_info.directory().c_str());
 Trace_file.open(filename);
 
 //Parameter incrementation
 double delta_p=0.0125;
 unsigned nstep=21; 
 
 // Perform fewer steps if run as self-test (indicated by nonzero number
 // of command line arguments)
 if (CommandLineArgs::Argc!=1)
  {
   nstep=3;
  }
 
 // Offset external pressure so that the computation sweeps 
 // over a range of positive and negative pressures
 Global_Physical_Variables::P =-delta_p*double(nstep-1)*0.5; 
 
 // Do the parameter study
 for(unsigned i=0;i<nstep;i++)
  {
   //Solve the problem for current load
   newton_solve();
 
   // Doc solution
   doc_solution(doc_info);
   doc_info.number()++;
 
   // Increment pressure load
   Global_Physical_Variables::P += delta_p;   
  }
 
} // end of parameter study

Comments and Exercises

The use of MacroElements in solid mechanics problems

Recall how oomph-lib employs MacroElements to represent the exact domain shapes in adaptive computations involving problems with curvilinear boundaries. When an element is refined, the (Eulerian) position of any newly-created nodes is based on the element's MacroElement counterpart, rather than being determined by finite-element interpolation from the "father element". This ensures that (i) newly-created nodes on curvilinear domain boundaries are placed exactly onto those boundaries and (ii) that newly-created nodes in the interior are placed at positions that match smoothly onto the boundary.

This strategy is adapted slightly for solid mechanics problems:

The Eulerian position of newly-created SolidNodes is determined by finite element interpolation from the "father element", unless the newly-created SolidNode is located on a domain boundary and its position is pinned by displacement boundary conditions.
The same procedure is employed to determine the Lagrangian coordinates of newly-created SolidNodes.

These modifications ensure that, as before, newly-created nodes on curvilinear domain boundaries are placed exactly onto those boundaries if their positions are pinned by displacement boundary conditions. (If the nodal positions are not pinned, the node's Eulerian position will be determined as part of the solution.) The use of finite-element interpolation from the "father element" in the interior of the domain for both Lagrangian and Eulerian coordinates ensures that the creation of new nodes does not induce any stresses into a previously computed solution.

Exercises

Our discretisation of the problem in cartesian coordinates did not exploit the problem's axisymmetry. Examine the trace file to assess to which extent the computation retained the axisymmetry.

PDF file

A pdf version of this document is available.