In this document we discuss the solution of a time-dependent beam problem: The large-amplitude oscillations of a thin-walled elastic ring. Specifically we shall

demonstrate how to specify initial conditions for time-dependent simulations with oomph-lib's KirchhoffLoveBeam elements,
demonstrate how to use the dump/restart functions for KirchhoffLoveBeam elements,
show that timesteppers from the Newmark family
- can be used with variable timesteps,
- conserve energy,
- can allocate and maintain storage for the solution at previous timesteps.

Large-amplitude oscillations of a thin-walled elastic beam

We wish to compute the large-amplitude oscillations of a linearly-elastic, circular ring of undeformed radius and wall thickness , subject to a transient pressure load

$p_{ext}\left(\xi ,t \right) = \left\{ \begin{array}{ll} -P_{cos}\cos\left(2\xi\right) & \mbox{for $t<T_{kick}$} \\ 0 & \mbox{for $t>T_{kick}$} \end{array} \right. \mbox{\ \ \ \ \ \ \ \ \ \ (1) }$

which initiates an oscillation in which the ring deforms into a non-axisymmetric mode, as indicated in the sketch below: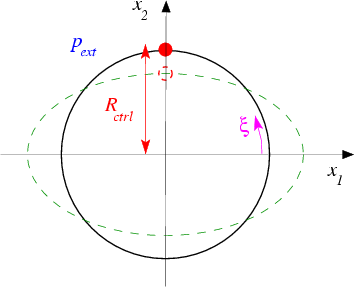

Sketch of the buckling ring.

We choose the same non-dimensionalisation as in the previous steady example and parametrise the position vector to the ring's undeformed centreline as

${\bf r}_w(\xi) = {\bf R}_w(\xi,t=0) = \left( \begin{array}{c} \cos(\xi) \\ \sin(\xi) \end{array} \right),$

where the non-dimensional arclength $\xi \in [0,2\pi]$ along the ring's undeformed centreline acts as the Lagrangian coordinate. Assuming that the ring is at rest for $t\le 0$ , we wish to compute the position vector to the deformed ring's centreline, ${\bf R}_w(\xi,t)$ , for .

Results

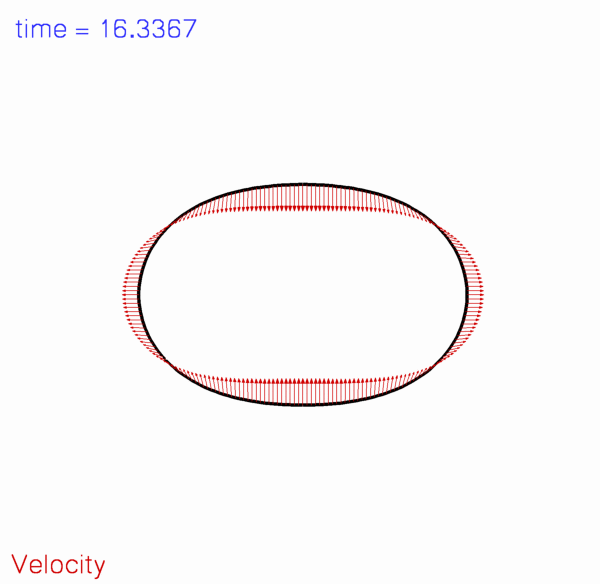
The figure below shows a snapshot, taken from an animation of the ring's computed deformation for a wall thickness of , a pressure load of $p_{cos} = 1.0 \times 10^{-4}$ , and $T_{kick} = 15$ . The arrows represent the instantaneous velocity of the ring and show that at this point in time the ring is still collapsing inwards.

Shape and velocity of the ring.

The red line with square markers in the figure below shows the time-history of the ring's control displacement: At the ring is in its initial undeformed configuration and we have $R_{ctrl} = 1$ . Application of the cosinusoidal pressure load during the interval $0 < t < T_{kick} = 15$ causes the ring to deform non-axisymmetrically in the mode shape shown in the plot above. Because of inertia, the ring continues to collapse inwards even after the pressure load has been "switched off". The ring reaches its most strongly collapsed configuration, in which the radius of the control point is reduced to just above 20% of its original value, at $t \approx 50$ . Subsequently, the elastic restoring forces cause the ring to "reopen" to its axisymmetric configuration (where $R_{ctrl}=1$ again), which it traverses with finite velocity at $t \approx 100$ . The ring overshoots the axisymmetric state and deforms in the "opposite" direction to the deformation during the initial stages of collapse. It reverses its motion again when it reaches a second non-axisymmetric extreme at $t \approx 150$ . This is seen most clearly in the animation of the ring's motion.

Plot of the control radius, the kinetic and potential (=strain) energy and their sum.

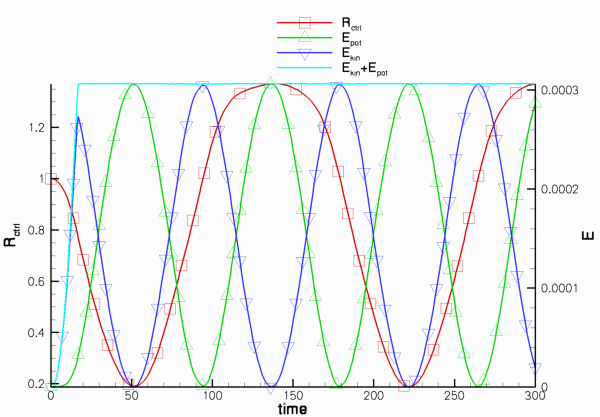
The remaining lines in the plot show the ring's kinetic and potential (i.e. the strain) energy and their sum. Up to $t = T_{kick}$ , the external load does work on the ring and increases its kinetic and potential (strain) energy. Once the external load is "switched off" the total energy stored in the system should (and indeed does) remain constant. See the section The default non-dimensionalisation for the kinetic and potential (strain) energies for further details.

Global parameters and functions

As usual, we employ a namespace to define the problem's physical parameters and the load that acts on the ring. For the pressure loading defined in equation (1), the load is given by

$\mathbf{f} = -P_{cos}\cos\left(2\xi\right)\mathbf{N},$

where $\mathbf{N}$ is the outer unit normal to the ring's deformed centreline.

//====start_of_namespace============================
/// Namespace for global parameters
//==================================================
namespace Global_Physical_Variables
{
 
 /// Perturbation pressure
 double Pcos;
 
 /// Duration of transient load
 double T_kick;
 
 /// Load function: Perturbation pressure to force non-axisymmetric deformation
 void press_load(const Vector<double>& xi,
                 const Vector<double> &x,
                 const Vector<double>& N,
                 Vector<double>& load)
 {
  for(unsigned i=0;i<2;i++) 
   {
    load[i] = -Pcos*cos(2.0*xi[0])*N[i];
   }
 } //end of load

We also define the non-dimensional wall thickness and the timescale ratio $\Lambda^2$ . These are multiplied by powers of a scaling factor whose role will become apparent in the Exercises. (By default, the scaling factor is set to 1.0 and does not play any role.)

 
 
 /// Scaling factor for wall thickness (to be used in an exercise)
 double Alpha=1.0;
 
 /// Wall thickness -- 1/20 for default value of scaling factor
 double H=Alpha*1.0/20.0;
 
 /// Square of timescale ratio (i.e. non-dimensional density)  
 /// -- 1.0 for default value of scaling factor
 double Lambda_sq=pow(Alpha,2);
 
} // end of namespace

The driver code

The main function is very simple. We store the (up to) two optional command line arguments which (if present) specify (i) a flag that indicates if the code is run in validation mode, and (ii) the name of a restart file.

//===start_of_main=====================================================
/// Driver for oscillating ring problem 
//=====================================================================
int main(int argc, char* argv[])
{
 
 // Store command line arguments
 CommandLineArgs::setup(argc,argv);

Next, we build the problem with thirteen HermiteBeamElements and a Newmark<3> timestepper ( recall that a Newmark<NSTEPS> timestepper allocates and manages storage for the solution at NSTEPS previous timesteps; we shall illustrate this capability in the section How to retrieve the solution at previous timesteps ), before executing the timestepping loop.

 
 // Number of elements
 unsigned nelem = 13;
 
 //Set up the problem
 ElasticRingProblem<HermiteBeamElement,Newmark<3> > problem(nelem);
 
 // Do unsteady run
 problem.unsteady_run();
 
} // end of main

The problem class

The problem class is very similar to that used in the previous, steady example , but includes a few (obvious) additional functions that specify the initial conditions (Setting the initial condition) and perform the timestepping (The timestepping loop). We also provide two functions that allow us to dump the solution to disk (Writing a restart file) and to restart the time-dependent simulation (Restarting from a file).

//===start_of_problem_class=============================================
/// Ring problem
//======================================================================
template<class ELEMENT, class TIMESTEPPER>
class ElasticRingProblem : public Problem
{
 
public:
 
 /// Constructor: Number of elements
 ElasticRingProblem(const unsigned& n_element);
 
 /// Access function for the specific mesh
 OneDLagrangianMesh<ELEMENT>* mesh_pt() 
  {
   return dynamic_cast<OneDLagrangianMesh<ELEMENT>*>(Problem::mesh_pt());
  }
 
 /// Update function is empty 
 void actions_after_newton_solve() {}
 
 /// Update function is empty 
 void actions_before_newton_solve() {}
 
 /// Setup initial conditions
 void set_initial_conditions();
 
 /// Doc solution
 void doc_solution(DocInfo& doc_info);
 
 /// Do unsteady run
 void unsteady_run();
 
 /// Dump problem-specific parameter values, then dump
 /// generic problem data.
 void dump_it(ofstream& dump_file);
 
 /// Read problem-specific parameter values, then recover
 /// generic problem data.
 void restart(ifstream& restart_file);

The private member data includes an output stream that we shall use to write a trace file. The two boolean flags indicate if the code is run in validation mode, and if the simulation has been restarted, respectively.

 
private:
 
 /// Trace file for recording control data
 ofstream Trace_file;
 
 /// Flag for validation run: Default: 0 = no validation run
 unsigned Validation_run_flag;
 
 /// Restart flag specified via command line?
 bool Restart_flag;
 
}; // end of problem class

The problem constructor

The constructor assigns default values for the two control flags corresponding to a non-validation run without restart. We create a timestepper of the type specified by the template parameter and add it to the Problem's collection of timesteppers.

//===start_of_constructor===============================================
/// Constructor for elastic ring problem
//======================================================================
template<class ELEMENT,class TIMESTEPPER>
ElasticRingProblem<ELEMENT,TIMESTEPPER>::ElasticRingProblem
(const unsigned& n_element) :
 Validation_run_flag(0), //default: false
 Restart_flag(false)
{
 
 // Create the timestepper and add it to the Problem's collection of
 // timesteppers -- this creates the Problem's Time object.
 add_time_stepper_pt(new TIMESTEPPER());

Next we build the geometric object that defines the shape of the ring's undeformed centreline (an ellipse with unit half axes, i.e. a unit circle) and use it to build the mesh. As in the previous steady example we exploit the symmetry of the deformation and only discretise a quarter of the domain.

 
 // Undeformed beam is an ellipse with unit axes
 GeomObject* undef_geom_pt=new Ellipse(1.0,1.0); 
 
 //Length of domain
 double length = MathematicalConstants::Pi/2.0;
 
 //Now create the (Lagrangian!) mesh
 Problem::mesh_pt() = new OneDLagrangianMesh<ELEMENT>(
  n_element,length,undef_geom_pt,Problem::time_stepper_pt()); 

The boundary conditions are identical to those in the steady example.

 
 // Boundary condition: 
 
 // Bottom: 
 unsigned ibound=0;
 // No vertical displacement
 mesh_pt()->boundary_node_pt(ibound,0)->pin_position(1); 
 // Zero slope: Pin type 1 (slope) dof for displacement direction 0 
 mesh_pt()->boundary_node_pt(ibound,0)->pin_position(1,0);
 
 // Top: 
 ibound=1;
 // No horizontal displacement
 mesh_pt()->boundary_node_pt(ibound,0)->pin_position(0); 
 // Zero slope: Pin type 1 (slope) dof for displacement direction 1
 mesh_pt()->boundary_node_pt(ibound,0)->pin_position(1,1); 

Finally, we pass the pointers to the load function and the pointer to the geometric object that specifies the ring's initial shape to the elements and assign the equation numbers.

 
 // Complete build of all elements so they are fully functional
 // -----------------------------------------------------------
 
 //Loop over the elements to set physical parameters etc.
 for(unsigned i=0;i<n_element;i++)
  {
   // Cast to proper element type
   ELEMENT *elem_pt = dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(i));
   
   // Pass pointer to square of timescale ratio (non-dimensional density)
   elem_pt->lambda_sq_pt() = &Global_Physical_Variables::Lambda_sq;
 
   // Pass pointer to non-dimensional wall thickness
   elem_pt->h_pt() = &Global_Physical_Variables::H;
 
   // Function that specifies load vector
   elem_pt->load_vector_fct_pt() = &Global_Physical_Variables::press_load;
   
   // Assign the undeformed surface
   elem_pt->undeformed_beam_pt() = undef_geom_pt;
  }
 
 // Do equation numbering
 cout << "# of dofs " << assign_eqn_numbers() << std::endl;
 
} // end of constructor

Post-processing

We compute the total kinetic and potential (=strain) energies stored in the (quarter-)ring and document them, their sum, and the control radius in the trace file.

//====start_of_doc_solution===============================================
/// Document solution
//========================================================================
template<class ELEMENT, class TIMESTEPPER>
void ElasticRingProblem<ELEMENT, TIMESTEPPER>::doc_solution(
 DocInfo& doc_info)
{ 
 
 cout << "Doc-ing step " <<  doc_info.number()
      << " for time " << time_stepper_pt()->time_pt()->time() << std::endl;
 
 
 // Loop over all elements to get global kinetic and potential energy
 unsigned n_elem=mesh_pt()->nelement();
 double global_kin=0;
 double global_pot=0;
 double pot,kin;
 for (unsigned ielem=0;ielem<n_elem;ielem++)
  {
   dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(ielem))->get_energy(pot,kin);
   global_kin+=kin;
   global_pot+=pot;
  }
  
 
 // Get pointer to last element to document displacement
 FiniteElement* trace_elem_pt=mesh_pt()->finite_element_pt(n_elem-1);
 
 // Vector of local coordinates at control point
 Vector<double> s_trace(1);
 s_trace[0]=1.0;
 
 // Write trace file: Time, control position, energies
 Trace_file << time_pt()->time()  << " " 
            << trace_elem_pt->interpolated_x(s_trace,1) 
            << " " << global_pot  << " " << global_kin
            << " " << global_pot + global_kin
            << std::endl; // end of output to trace file

Next we use the default output function to document the ring shape and add a few tecplot commands to facilitate the animation of the results.

  
 ofstream some_file;
 char filename[100];
  
 // Number of plot points
 unsigned npts=5;
  
 // Output solution 
 sprintf(filename,"%s/ring%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 mesh_pt()->output(some_file,npts);
 
 // Write file as a tecplot text object
 some_file << "TEXT X=2.5,Y=93.6,F=HELV,HU=POINT,C=BLUE,H=26,T=\"time = " 
           << time_pt()->time() << "\"";
 
 // ...and draw a horizontal line whose length is proportional
 // to the elapsed time
 some_file << "GEOMETRY X=2.5,Y=98,T=LINE,C=BLUE,LT=0.4" << std::endl;
 some_file << "1" << std::endl;
 some_file << "2" << std::endl;
 some_file << " 0 0" << std::endl;
 some_file << time_pt()->time()*20.0 << " 0" << std::endl;
 some_file.close();

How to retrieve the solution at previous timesteps

The next few lines illustrate how to retrieve (and document) the ring shape at previous timesteps. Recall that Newmark timesteppers are implicit, single-step timestepping schemes that compute approximations for the time-derivatives, based on the solution at the current time level, and on "history values" that represent quantities at a single previous timestep. In some applications (particularly in fluid-structure interaction problems) it is necessary to keep track of the solution at additional previous timesteps. Storage for such additional history values is allocated (and managed) by the generalised Newmark<NSTEPS> timesteppers if NSTEPS > 1. We stress that these additional history values are not involved in the approximation of the time-derivatives; they are simply stored and updated by the timestepper when the solution is advanced to the next timestep.

Recall also that the member function TimeStepper::nprev_values() may be used to determine how many of the history values that are stored in an associated Data object represent the solution at previous timesteps. Finally, recall that history values that represent the solution at previous timesteps are always stored before those that represent "generalised" history values (such as approximations of the first time-derivative at the previous timestep, etc). It is therefore always possible to determine how many previous solutions are stored in a Data object, and where they are stored.

To document the shape of a HermiteBeamElement at a previous timestep, the HermiteBeamElement provides an additional three-argument output function that may be called as follows:

 
 
 // Loop over all elements do dump out previous solutions
 unsigned nsteps=time_stepper_pt()->nprev_values();
 for (unsigned t=0;t<=nsteps;t++)
  {     
   sprintf(filename,"%s/ring%i-%i.dat",doc_info.directory().c_str(),
           doc_info.number(),t);
   some_file.open(filename);
   unsigned n_elem=mesh_pt()->nelement();
   for (unsigned ielem=0;ielem<n_elem;ielem++)
    {
     dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(ielem))->
      output(t,some_file,npts);
    }
   some_file.close();
  } // end of output of previous solutions

At timestep t, these statements create the output files RESLT/ring t-0.dat, RESLT/ring t-1.dat, RESLT/ring t-2.dat, RESLT/ring t-3.dat, which contain the shape of the ring at the t -th, ( t -1)th, ( t -2)th and
( t -3)th, timestep, respectively.

Finally, we write a restart file that will allow us to restart the simulation.

  
 
 // Write restart file
 sprintf(filename,"%s/ring_restart%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 dump_it(some_file);
 some_file.close();
 
       
} // end of doc solution

Writing a restart file

Writing the restart file for the present problem is as easy as in the previous examples, as the generic Problem data may again be written with the Problem::dump(...) function. We customise the restart file slightly by adding the value $p_{cos}$ and the flag that indicates if the code is run in validation mode.

//===start_of_dump_it====================================================
/// Dump problem-specific parameter values, then dump
/// generic problem data.
//=======================================================================
template<class ELEMENT,class TIMESTEPPER>
void ElasticRingProblem<ELEMENT,TIMESTEPPER>::dump_it(ofstream& dump_file)
 
{
  
 // Write Pcos
 dump_file << Global_Physical_Variables::Pcos << " # Pcos" << std::endl;
 
 // Write validation run flag
 dump_file << Validation_run_flag 
           << " # Validation run flag" << std::endl;
 
 // Call generic dump()
 Problem::dump(dump_file);
 
} // end of dump it

Restarting from a file

The restart operation reverses the steps performed in the dump function: We recover the two problem-specific parameters and then read the generic Problem data with the Problem::read(...) function.

//==start_of_restart=====================================================
/// Read problem-specific parameter values, then recover
/// generic problem data.
//=======================================================================
template<class ELEMENT,class TIMESTEPPER>
void ElasticRingProblem<ELEMENT,TIMESTEPPER>::restart(ifstream& restart_file)
{
  
 string input_string;
 
 // Read line up to termination sign
 getline(restart_file,input_string,'#');
 // Ignore rest of line
 restart_file.ignore(80,'\n');
 // Read in pcos
 Global_Physical_Variables::Pcos=atof(input_string.c_str());
 
 // Read line up to termination sign
 getline(restart_file,input_string,'#');
 // Ignore rest of line
 restart_file.ignore(80,'\n');
 // Read in Long run flag
 Validation_run_flag=
  unsigned(atof(input_string.c_str()));
 
 // Call generic read()
 Problem::read(restart_file);
 
} // end of restart

Setting the initial condition

The assignment of initial conditions depends on whether or not a restart from a previous computation is performed. If no restart is performed, we specify the initial timestep, dt, and assign history values that are consistent with an impulsive start from the ring's initial shape.

//=====start_of_set_ic=====================================================
/// Setup initial conditions -- either restart from solution 
/// specified via command line or impulsive start. 
//=========================================================================
template<class ELEMENT,class TIMESTEPPER>
void ElasticRingProblem<ELEMENT,TIMESTEPPER>::set_initial_conditions()
{
 
 // No restart file --> impulsive start from initial configuration
 // assigned in the Lagrangian mesh.
 if (!Restart_flag)
  {
   // Set initial timestep
   double dt=1.0; 
 
   // Assign impulsive start
   assign_initial_values_impulsive(dt);
  }

If the computation is restarted, the name of the restart file will have been specified on the command line. We try to open the restart file

 // Restart file specified via command line
 else
  {
   // Try to open restart file
   ifstream* restart_file_pt= 
    new ifstream(CommandLineArgs::Argv[2],ios_base::in);
   if (restart_file_pt!=0)
    {
     cout << "Have opened " << CommandLineArgs::Argv[2] << 
      " for restart. " << std::endl;
    }

and display an error message and terminate the program execution if the file cannot be opened.

   else
    {
     std::ostringstream error_stream;
     error_stream << "ERROR while trying to open " 
                  << CommandLineArgs::Argv[2] 
                  << " for restart." << std::endl;
 
     throw OomphLibError(error_stream.str(),
                         OOMPH_CURRENT_FUNCTION,
                         OOMPH_EXCEPTION_LOCATION);
    }

If the file can be opened we call the restart function which returns the the Problem into the state it was in when the restart file was written. No further steps are required.

 
   // Read restart data:
   restart(*restart_file_pt);
 
  }
 
} // end of set ic

The timestepping loop

We start by converting the (optional) command line arguments into the flags that determine what mode the code is run in: Without command line arguments, we use the default assignments, as specified in The problem constructor.

//===start_of_unsteady_run=================================================
/// Solver loop to perform unsteady run.
//=========================================================================
template<class ELEMENT,class TIMESTEPPER>
void ElasticRingProblem<ELEMENT,TIMESTEPPER>::unsteady_run()
{
 
 // Convert command line arguments (if any) into flags:
 //----------------------------------------------------
 
 if (CommandLineArgs::Argc<2)
  {
   cout << "No command line arguments -- using defaults." 
        << std::endl;
  }

A single command line argument is interpreted as the "validation run" flag (1 for true, 0 for false) which will be used to limit the number of timesteps.

 else if (CommandLineArgs::Argc==2)
  {
   // Flag for validation run
   Validation_run_flag=atoi(CommandLineArgs::Argv[1]);
  }

The presence of two command line arguments indicates that a restart is performed. In this case the second argument specifies the name of the restart file.

 else if (CommandLineArgs::Argc==3)
  {
   // Flag for validation run
   Validation_run_flag=atoi(CommandLineArgs::Argv[1]);
 
   // Second argument is restart file. If it's there we're performing
   // a restart
   Restart_flag=true;
  }

We print an error message if the code is run with any other number of command line arguments.

 else
  {
   std::string error_message =
    "Wrong number of command line arguments. Specify two or fewer.\n";
   error_message += "Arg1: Validation_run_flag [0/1] for [false/true]\n";
   error_message += "Arg2: Name of restart_file (optional)\n";
   error_message += "No arguments specified --> default run\n";
   
   throw OomphLibError(error_message,
                       OOMPH_CURRENT_FUNCTION,
                       OOMPH_EXCEPTION_LOCATION);
  }

We create a DocInfo object to specify the name of the output directory, and open the trace file.

 
 
 // Label for output
 DocInfo doc_info;
 
 // Output directory
 doc_info.set_directory("RESLT");
 
 // Step number
 doc_info.number()=0;
 
 // Set up trace file
 char filename[100];
 sprintf(filename,"%s/trace_ring.dat",doc_info.directory().c_str());
 Trace_file.open(filename);
 
 Trace_file <<  "VARIABLES=\"time\",\"R<sub>ctrl</sub>\",\"E<sub>pot</sub>\"";
 Trace_file << ",\"E<sub>kin</sub>\",\"E<sub>kin</sub>+E<sub>pot</sub>\"" 
            << std::endl;

Next, we set the problem parameters and the number of timesteps to be performed, before assigning the initial conditions.

 
 // Perturbation pressure -- incl. scaling factor (Alpha=1.0 by default)
 Global_Physical_Variables::Pcos=1.0e-4
  *pow(Global_Physical_Variables::Alpha,3); 
 
 // Duration of transient load
 Global_Physical_Variables::T_kick=15.0;
 
 // Number of steps
 unsigned nstep=600; 
 if (Validation_run_flag==1) {nstep=10;}
 
 // Setup initial condition (either restart or impulsive start)
 set_initial_conditions();

The timestepping loop itself is practically identical to that used in driver codes for other unsteady problems. To demonstrate that Newmark timesteppers can deal with variable timesteps, we reduce the timestep slightly after every step.

 
 // Extract initial timestep as set up in set_initial_conditions()
 double dt=time_pt()->dt();
 
 // Output initial data
 doc_solution(doc_info);
 
 // If the run is restarted, dt() contains the size of the timestep
 // that was taken to reach the dumped solution. In a non-restarted run
 // the next step would have been taken with a slightly smaller 
 // timestep (see below). For a restarted run we therefore adjust 
 // the next timestep accordingly.
 if (Restart_flag&&(time_pt()->time()>10.0)&&(time_pt()->time()<100.0))
  {
   dt=0.995*dt;
  }
 
 // Time integration loop
 for(unsigned i=1;i<=nstep;i++)
  {
   // Switch off perturbation pressure 
   if (time_pt()->time()>Global_Physical_Variables::T_kick) 
     {
      /// Perturbation pressure
      Global_Physical_Variables::Pcos=0.0; 
     }
   
   // Solve
   unsteady_newton_solve(dt);
   
   // Doc solution
   doc_info.number()++;
   doc_solution(doc_info);
   
   // Reduce timestep for the next solve
   if ((time_pt()->time()>10.0)&&(time_pt()->time()<100.0))
    {
     dt=0.995*dt;
    }
 
  }
 
} // end of unsteady run

Comments and Exercises

The default non-dimensionalisation of time

The non-dimensionalisation of the principle of virtual displacements that forms the basis of oomph-lib's beam elements, was discussed in detail in an earlier example. However, since this is the first time-dependent beam problem it is worth re-iterating that, by default, time is non-dimensionalised on the timescale for extensional deformations i.e. on the natural timescale

${\cal T}_{natural} = {\cal L} \sqrt{\frac{\rho}{E_{eff}}}$

of oscillations in which the beam is stretched/compressed along its centreline. The relation between the dimensional time and its non-dimensional equivalent is given by

$t^* = \underbrace{{\cal L} \sqrt{\frac{\rho}{E_{eff}}}}_{{\cal T}_{natural}} \ t,$

where ${\cal L}$ is the lengthscale used to non-dimensionalise all lengths (in the present example ${\cal L} = R_0$ , the undeformed radius of the ring), $\rho$ is the density of the ring, and $E_{eff} = E/(1-\nu^2)$ is the "effective" 1D Young's modulus of the beam, formed with its 3D Young's modulus , and its Poisson ratio $\nu$ .

This non-dimensionalisation of time is consistent with the non-dimensionalisation of all stresses/loads on $E_{eff}$ . It implies that if the beam deforms in a mode in which its deformation is dominated by bending effects, the numerical values for the non-dimensional load are relatively small (indicating that the loads required to induce a deformation of a given size are much smaller if the ring deforms in a bending-dominated mode, than in a mode in which it is dominated by extensional deformations), while the non-dimensional period of the oscillation is relatively large (indicating that bending oscillations occur at a much smaller frequency than oscillations in which the beam's deformation is dominated by extensional deformations).

The default non-dimensionalisation for the kinetic and potential (strain) energies

With the default non-dimensionalisation discussed above, the non-dimensional kinetic and potential (strain) energies are given by

$\Pi_{strain} = \frac{\Pi_{strain}^*}{{\cal L} \, h^* E_{eff} } = \frac{1}{2}\int \left( \gamma^2 + \frac{1}{12}\left(\frac{h^*}{{\cal L}}\right)^2 \kappa^2 \right) \ d \xi$

and

$\Pi_{kin} = \frac{\Pi_{kin}^*}{{\cal L} \, h^* E_{eff}} = \frac{1}{2} \int \frac{\partial {\bf R}_w}{\partial t} \cdot \frac{\partial {\bf R}_w}{\partial t} \ d \xi,$

respectively. Conservation of energy implies that

$\Pi_{kin} + \Pi_{strain} = const.$

if there is no external forcing. The plot of the energies shown at the beginning of this document shows that the time-integration with the Newmark method is energy-conserving.

Changing the timescale used to non-dimensionalise the equations

It is possible to non-dimensionalise the governing equations on a different timescale, ${\cal T}$ , so that

$t^* = {\cal T} \ t.$

This is achieved by overwriting the default assignment for the ratio

$\Lambda = \frac{{\cal T}_{natural}}{{\cal T}} = \frac{{\cal L}}{{\cal T}} \sqrt{\frac{\rho}{E_{eff}}},$

of the natural timescale ${\cal T}_{natural}$ and the time ${\cal T}$ used to non-dimensionalise the equations.

By default, we have $\Lambda = 1$ but the member function

KirchhoffLoveBeamEquations::lambda_sq_pt()

may be used to assign a different value for the square of the timescale ratio which may also be interpreted as the non-dimensional density. The case $\Lambda^2=0$ therefore corresponds to the case of zero wall inertia. (We store $\Lambda^2$ rather than $\Lambda$ itself because the governing equations contain only the square of the timescale ratio). As with most other physical parameters, $\Lambda^2$ must be defined as a global variable, preferably by adding it to the namespace that contains the problem parameters, e.g.

//====start_of_namespace============================
/// Namespace for global parameters
//==================================================
namespace Global_Physical_Variables
{
 
 /// Square of timescale ratio, i.e. the non-dimensional density
 double Lambda_sq=4.0;
 
 [...]
 
} // end of namespace

...and passing a pointer to $\Lambda^2$ to the elements. The statement can be added to the loop over the elements that passes the pointer to the pressure load to the elements.

//Loop over the elements to set physical parameters etc.
for(unsigned i=0;i<n_element;i++)
 {
  // Cast to proper element type
  ELEMENT *elem_pt = dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(i));
  
  // Pass pointer to square of timescale ratio (non-dimensional density)
  elem_pt->lambda_sq_pt() = &Global_Physical_Variables::Lambda_sq;
 
  [...]
 
 }

The definition of the non-dimensional kinetic energy used in KirchhoffLoveBeamEquations::get_energy(...) incorporates the timescale ratio by computing the non-dimensional kinetic energy as

$\Pi_{kin} = \frac{\Pi_{kin}^*}{{\cal L} \, h^* E_{eff}} = \frac{1}{2} \Lambda^2 \int \frac{\partial {\bf R}_w}{\partial t} \cdot \frac{\partial {\bf R}_w}{\partial t} \ d \xi$

which, for the default assignment $\Lambda^2 = 1$ , reduces to the definition given above.

Exercises

As discussed in The default non-dimensionalisation of time , the period of the oscillation ( 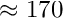) computed in the above example has a large numerical value because time was non-dimensionalised on a timescale that is representative for oscillations in which the ring's motion is dominated by extensional (rather than bending) deformations. Furthermore, because the load is non-dimensionalised on the ring's extensional (rather than its bending) stiffness, a very small load 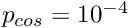was sufficient to induce large-amplitude oscillations.

Change the load function to a spatially-constant external pressure (which will deform the ring axisymmetrically so that its motion is dominated by extensional deformations) to confirm that in this mode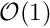
1. ${\cal O}(1)$ pressures are required to induce 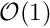${\cal O}(1)$ axisymmetric displacements, and
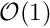2. the period of the axisymmetric oscillations is ${\cal O}(1)$ .

[Hint: You will have to reduce the timestep to capture the much faster axisymmetric oscillations.]

Use the principle of virtual displacements (without prestress)
$\int_0^{L} \left[ \gamma \ \delta \gamma + \frac{1}{12} h^2 \kappa \ \delta \kappa - \left(\frac{1}{h} \sqrt{\frac{A}{a}} \ {\bf f} - \Lambda^2 \frac{\partial^2 {\bf R}_w}{\partial t^2} \right) \cdot \delta {\bf R}_w \right] \ \sqrt{a} \ d\xi = 0, \ \ \ \ \ \ \ \ \ (2)$
to show (analytically) that for bending-dominated deformations (i.e. deformations for which )
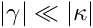1. an increase in the wall thickness 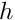by a factor 2, say, will
  1. reduce the amplitude of the ring's static deformation by a factor of 8 (thicker rings are stiffer)
  2. reduces the period of the unforced oscillations (i.e. the oscillations it performs when 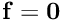${\bf f} = {\bf 0}$ ) by factor of 4 (thicker rings oscillate more rapidly).

an increase in the ring's density 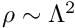$\rho \sim \Lambda^2$ by a factor of 2, say, increases the period of its bending-dominated oscillations by a factor of 4 (heavier rings oscillate more slowly).

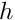Combine these results to show that a ring of wall thickness and a density 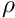$\rho$ , subject to a forcing of magnitude 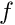will deform (approximately) as a ring of wall thickness 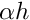$\alpha h$ with a density 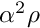$\alpha^2 \rho$ , subject to a forcing of magnitude 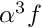$\alpha^3 f$ . Confirm these theoretical predictions computationally: Change the initial assignment for the scaling factor Global_Physical_Variables::Alpha and repeat the computation.

Confirm that the restart procedure works correctly by plotting the time-trace obtained from a restarted simulation on top of the original time-trace.
Compare the results obtained from a simulation with a variable timestep against the results obtained from a computation with a fixed timestep (comment out the line that reduces the timestep after every solve).
Compare the various output files generated in doc_solution() to confirm that the Newmark<3> timestepper correctly maintains the history of the solution at three previous timesteps. E.g. confirm that the output file RESLT/ring3-0.dat which contains the ring shape at timestep 3 is identical to RESLT/ring5-2.dat which contains the ring shape computed two timesteps before timestep 5. Explore oomph-lib's internal use of the history values by analysing the functions
HermiteBeamElement::output(...)

FiniteElement::interpolated_x(...)

and
FiniteElement::x_gen(...)

Source files for this tutorial

The source files for this tutorial are located in the directory: demo_drivers/beam/unsteady_ring/
The driver code is: demo_drivers/beam/unsteady_ring/unsteady_ring.cc

PDF file

A pdf version of this document is available.