Demo problem: Bending of a 3D non-symmetric cantilever beam made of incompressible material

In this tutorial we demonstrate the solution of a 3D solid mechanics problem: the large-amplitude bending deformation of a non-symmetric cantilever beam made of incompressible Mooney-Rivlin material.

Here is an animation of the beam's deformation. In its undeformed configuration, the beam is straight and its cross-section is given by a quarter circle. The beam is loaded by an increasing gravitational body force, acting in the negative -direction, while its left end (at ) is held fixed. Because of its non-symmetric cross-section, the beam's downward bending deformation is accompanied by a sideways deflection.

Animation of the beam's bending deformation.

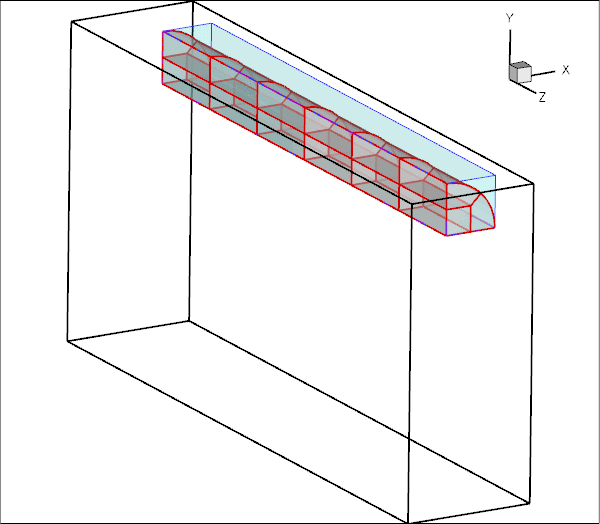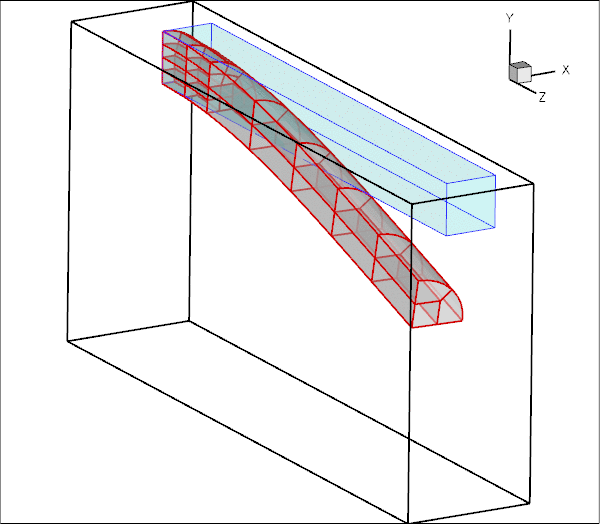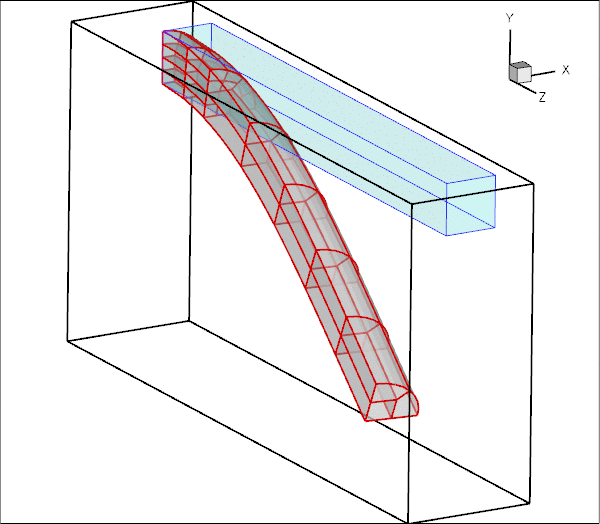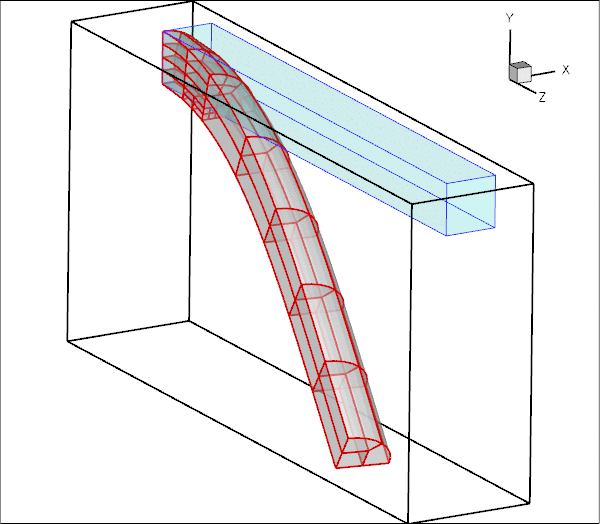
Note how the automatic mesh adaptation refines the mesh in the region of strongest bending.

---

---

The mesh

We use multiple inheritance to upgrade the already-existing refineable "quarter tube mesh" to a solid mesh. Following a call to the constructor of the underlying meshes, we set the nodes' Lagrangian coordinates to their current Eulerian positions to make the initial configuration stress-free.

//======================start_mesh=========================================
/// Simple quarter tube mesh upgraded to become a solid mesh
//=========================================================================
template<class ELEMENT>
class RefineableElasticQuarterTubeMesh : 
 public virtual RefineableQuarterTubeMesh<ELEMENT>, 
 public virtual SolidMesh 
{
 
public:
 
 /// Constructor: 
 RefineableElasticQuarterTubeMesh(GeomObject* wall_pt,
                                  const Vector<double>& xi_lo,
                                  const double& fract_mid,
                                  const Vector<double>& xi_hi,
                                  const unsigned& nlayer,
                                  TimeStepper* time_stepper_pt=
                                  &Mesh::Default_TimeStepper) :
  QuarterTubeMesh<ELEMENT>(wall_pt,xi_lo,fract_mid,xi_hi,
                           nlayer,time_stepper_pt),
  RefineableQuarterTubeMesh<ELEMENT>(wall_pt,xi_lo,fract_mid,xi_hi,
                                     nlayer,time_stepper_pt) 
  {
   //Assign the Lagrangian coordinates
   set_lagrangian_nodal_coordinates();
  }
 
 /// Empty Destructor
 virtual ~RefineableElasticQuarterTubeMesh() { }
 
};

---

---

Global parameters and functions

As usual, we define a namespace, Global_Physical_Variables, to define the problem parameters: the length of the cantilever beam, , a (pointer to) a strain energy function, the constitutive parameters and for the Mooney-Rivlin strain energy function, and a (pointer to) a constitutive equation. Finally, we define the gravitational body force which acts in the negative -direction.

//=======start_namespace==========================================
/// Global variables
//================================================================
namespace Global_Physical_Variables
{
 
 /// Length of beam
 double L=10.0;
 
 /// Pointer to strain energy function
 StrainEnergyFunction* Strain_energy_function_pt=0;
 
 /// First "Mooney Rivlin" coefficient 
 double C1=1.3;
 
 /// Second "Mooney Rivlin" coefficient 
 double C2=1.3;
 
 /// Pointer to constitutive law
 ConstitutiveLaw* Constitutive_law_pt=0;
 
 /// Non-dim gravity
 double Gravity=0.0;
 
 /// Non-dimensional gravity as body force
 void gravity(const double& time, 
              const Vector<double> &xi, 
              Vector<double> &b)
 {
  b[0]=0.0;
  b[1]=-Gravity;
  b[2]=0.0;
 }
 
} //end namespace

---

---

The driver code

If the code is executed without command line arguments we perform a single simulation. We start by creating the strain energy function and pass it to the constructor of the strain-energy-based constitutive equation. We then build the problem object, using oomph-lib's large-displacement Taylor-Hood solid mechanics elements which are based on a continuous-pressure/displacement formulation.

//=======start_of_main==================================================
/// Driver for 3D cantilever beam loaded by gravity
//======================================================================
int main(int argc, char* argv[])
{
 
 // Run main demo code if no command line arguments are specified
 if (argc==1)
  {
   
   // Create incompressible Mooney Rivlin strain energy function
   Global_Physical_Variables::Strain_energy_function_pt = 
    new MooneyRivlin(&Global_Physical_Variables::C1,
                     &Global_Physical_Variables::C2);
   
   // Define a constitutive law (based on strain energy function)
   Global_Physical_Variables::Constitutive_law_pt = 
    new IsotropicStrainEnergyFunctionConstitutiveLaw(
     Global_Physical_Variables::Strain_energy_function_pt);
   
   //Set up the problem with continous pressure/displacement
   CantileverProblem<RefineableQPVDElementWithContinuousPressure<3> > problem;

We document the initial configuration before starting a parameter study in which the magnitude of the gravitational body force is increased in small steps:

   
   // Doc solution
   problem.doc_solution();
   
   // Initial values for parameter values
   Global_Physical_Variables::Gravity=0.0;
   
   //Parameter incrementation
   unsigned nstep=10; 
   
   double g_increment=5.0e-4;   
   for(unsigned i=0;i<nstep;i++)
    {
     // Increment load
     Global_Physical_Variables::Gravity+=g_increment;
     
     // Solve the problem with Newton's method, allowing
     // up to max_adapt mesh adaptations after every solve.
     unsigned max_adapt=1;   
     problem.newton_solve(max_adapt);
     
     // Doc solution
     problem.doc_solution();    
    }
 
  } // end main demo code

If the code is executed with a non-zero number of command line arguments, it performs a large number of additional self tests that we will not discuss here. See the driver code three_d_cantilever.cc for details.

---

---

The problem class

The problem class contains the usual member functions. No action is required before the mesh adaptation; we overload the function Problem::actions_after_adapt() to pin the redundant solid pressure degrees of freedom afterwards.

//=============begin_problem============================================ 
/// Problem class for the 3D cantilever "beam" structure.
//====================================================================== 
template<class ELEMENT>
class CantileverProblem : public Problem
{
 
public:
 
 /// Constructor:
 CantileverProblem(); 
 
 /// Update function (empty)
 void actions_after_newton_solve() {}
 
 /// Update function (empty)
 void actions_before_newton_solve() {}
 
 /// Actions before adapt. Empty
 void actions_before_adapt(){}
 
 /// Actions after adapt
 void actions_after_adapt()
  {
   // Pin the redundant solid pressures (if any)
   PVDEquationsBase<3>::pin_redundant_nodal_solid_pressures(
    mesh_pt()->element_pt());
  }
 
 /// Doc the solution
 void doc_solution();

We overload the Problem::mesh_pt() function to return a pointer to the specific mesh used in this problem:

 /// Access function for the mesh
 RefineableElasticQuarterTubeMesh<ELEMENT>* mesh_pt()
  {
   return dynamic_cast<RefineableElasticQuarterTubeMesh<ELEMENT>*>(
    Problem::mesh_pt());
  }

The private member data stores a DocInfo object in which we will store the name of the output directory.

private:
 
 /// DocInfo object for output
 DocInfo Doc_info;
 
};

---

---

The problem constructor

We start by creating the GeomObject that defines the curvilinear boundary of the beam: a circular cylinder of unit radius.

//===========start_of_constructor======================================= 
/// Constructor: 
//====================================================================== 
template<class ELEMENT>
CantileverProblem<ELEMENT>::CantileverProblem() 
{
 
 // Create geometric object that defines curvilinear boundary of
 // beam: Elliptical tube with half axes = radius = 1.0
 double radius=1.0;
 GeomObject* wall_pt=new EllipticalTube(radius,radius);
 
 // Bounding Lagrangian coordinates
 Vector<double> xi_lo(2);
 xi_lo[0]=0.0;
 xi_lo[1]=0.0;
 
 Vector<double> xi_hi(2);
 xi_hi[0]= Global_Physical_Variables::L;
 xi_hi[1]=2.0*atan(1.0);

We build the mesh, using six axial layers of elements, before creating an error estimator and specifying the error targets for the adaptive mesh refinement.

 // # of layers
 unsigned nlayer=6;
 
 //Radial divider is located half-way along the circumference
 double frac_mid=0.5;
 
 //Now create the mesh 
 Problem::mesh_pt() = new RefineableElasticQuarterTubeMesh<ELEMENT>
  (wall_pt,xi_lo,frac_mid,xi_hi,nlayer);
 
 // Set error estimator
 dynamic_cast<RefineableElasticQuarterTubeMesh<ELEMENT>* >(
  mesh_pt())->spatial_error_estimator_pt()=new Z2ErrorEstimator;
 
 // Error targets for adaptive refinement
 mesh_pt()->max_permitted_error()=0.05;
 mesh_pt()->min_permitted_error()=0.005;

We complete the build of the elements by specifying the constitutive equation and the body force. We check that the element is based on a pressure/displacement formulation, and, if so, select an incompressible formulation. (This check is only required because the self-tests not shown here also include cases in which the problem is solved using a displacement-based formulation with compressible elasticity; see also the section How to enforce incompressibility below).

 // Complete build of elements
 unsigned n_element=mesh_pt()->nelement();
 for(unsigned i=0;i<n_element;i++)
  {
   // Cast to a solid element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(i));
   
   // Set the constitutive law
   el_pt->constitutive_law_pt() =
    Global_Physical_Variables::Constitutive_law_pt;
 
   // Set the body force
   el_pt->body_force_fct_pt() = Global_Physical_Variables::gravity;
 
   // Material is incompressble: Use incompressible displacement/pressure
   // formulation (if the element is pressure based, that is!)
   PVDEquationsWithPressure<3>* cast_el_pt = 
    dynamic_cast<PVDEquationsWithPressure<3>*>(mesh_pt()->element_pt(i));
   if (cast_el_pt!=0)
    {
     cast_el_pt->set_incompressible();
    }
 
  } // done build of elements

We fix the position of all nodes at the left end of the beam (on boundary 0) and pin any redundant solid pressures.

 
 
 // Pin the left boundary (boundary 0) in all directions
 unsigned b=0; 
 unsigned n_side = mesh_pt()->nboundary_node(b);
 
 //Loop over the nodes
 for(unsigned i=0;i<n_side;i++)
  {
   mesh_pt()->boundary_node_pt(b,i)->pin_position(0);
   mesh_pt()->boundary_node_pt(b,i)->pin_position(1);
   mesh_pt()->boundary_node_pt(b,i)->pin_position(2);
  }
 
 // Pin the redundant solid pressures (if any)
 PVDEquationsBase<3>::pin_redundant_nodal_solid_pressures(
  mesh_pt()->element_pt());

Finally, we assign the equation numbers and define the output directory.

 
 //Assign equation numbers
 assign_eqn_numbers();
 
 // Prepare output directory
 Doc_info.set_directory("RESLT");
  
} //end of constructor

---

---

Post-processing

The post-processing function doc_solution() simply outputs the shape of the deformed beam.

//==============start_doc===========================================
/// Doc the solution
//==================================================================
template<class ELEMENT>
void CantileverProblem<ELEMENT>::doc_solution()
{
 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned n_plot = 5; 
 
 // Output shape of deformed body
 sprintf(filename,"%s/soln%i.dat",Doc_info.directory().c_str(),
         Doc_info.number());
 some_file.open(filename);
 mesh_pt()->output(some_file,n_plot);
 some_file.close();
 
 // Increment label for output files
 Doc_info.number()++;
 
} //end doc

---

---

Comments and exercises

How to enforce incompressibility

We stress that the imposition of incompressibility must be requested explicitly via the element's member function incompressible(). Mathematically, incompressibility is enforced via a Lagrange multiplier which manifests itself physically as the pressure. Incompressibility can therefore only be enforced for elements that employ the pressure-displacement formulation of the principle of virtual displacements. This is why we the Problem constructor checked if the element is derived from the PVDEquationsWithPressure class before setting the element's incompressible flag to true.

As usual, oomph-lib provides self-tests that assess if the enforcement incompressibility (or the lack thereof) is consistent:

• The compiler will not allow the user to enforce incompressibility on elements that are based on the displacement form of the principle of virtual displacements.
  
  
• Certain constitutive laws, such as the Mooney-Rivlin law used in the present example require an incompressible formulation. If oomph-lib is compiled with the PARANOID flag, an error is thrown if such a constitutive law is used by an element for which incompressibility has not been requested.
  
  Recall that the default setting is not to enforce incompressibility!
  If the library is compiled without the PARANOID flag no warning will be issued but the results will be "wrong" at least in the sense that the material does not behave like an incompressible Mooney-Rivlin solid. In fact, it is likely that the Newton solver will diverge. Anyway, as we keep saying, without the PARANOID flag, you're on your own!
  
  
• Some constitutive laws can be used for compressible and incompressible behaviour. In this case it is important to set the incompressible() flag to the correct value. This issue is discussed in more detail in another tutorial.

You should experiment with different combinations of constitutive laws and element types to familiarise yourself with these.

---

---

Source files for this tutorial

• The source files for this tutorial are located in the directory:
  
  demo_drivers/solid/three_d_cantilever/
  
• The driver code is:
  
  demo_drivers/solid/three_d_cantilever/three_d_cantilever.cc

---

---

PDF file

A pdf version of this document is available.