The purpose of this tutorial is to discuss the use of compressible and incompressible constitutive equations for solid mechanics problems. As discussed in the Solid Mechanics Theory Tutorial, problems in which the solid is truly incompressible require a solution based on the pressure/displacement formulation of the principle of virtual displacements (PVD). Mathematically, this is because the pressure acts as the Lagrange multiplier that enforces incompressibility. The pressure/displacement form of the PVD may be discretised with finite elements that employ continuous (e.g. Taylor-Hood-type) or discontinuous (e.g. Crouzeix-Raviart-type) elements.

Some constitutive equations allow for compressible and incompressible behaviour, depending on their parameters. Problems involving such constitutive equations may be solved with large number of formulations. As an example, consider oomph-lib's generalised Hookean constitutive equation (see the disclaimer below).

I. The displacement form

oomph-lib's generalised Hookean constitutive law assumes that the 2nd Piola Kirchhoff stress $\sigma^{ij}$ (non-dimensionalised on Young's modulus ) is related to Green's strain tensor $\gamma_{ij} = 1/2 \ (G_{ij} - g_{ij})$ via

$\sigma^{ij} = \frac{1}{2(1+\nu)} \left( G^{ik} G^{jl} + G^{il} G^{jk} + \frac{2\nu}{1-2\nu} G^{ij} G^{kl} \right) \gamma_{kl}. \hspace{3cm} (1)$

Here $g_{ij}$ and $G_{ij}$ are the metric tensors associated with the undeformed and deformed configurations. This constitutive law reduces to the the classical version of Hooke's law for small strains when $G_{ij} \to g_{ij}.$ In the above form, the constitutive law can be used directly in the displacement-based form of the PVD, unless $\nu = 1/2$ – the case that corresponds to incompressible behaviour in the small-displacement regime. (While the above formulation only breaks down completely when $\nu = 1/2,$ numerical solutions based on the above form of the constitutive equation become badly-behaved as $\nu$ approaches that value.)

II. The pressure-displacement form for compressible and incompressible behaviour

To avoid the problems that arise as $\nu \to 1/2,$ the constitutive equation may be rewritten in the form

$\sigma^{ij} = \overline{\sigma}^{ij} - p \ G^{ij} \ ,$

where the deviatoric stress is given by

$\overline{\sigma}^{ij} = \frac{1}{2(1+\nu)} \bigg( G^{ik} G^{jl} + G^{il} G^{jk} \bigg) \gamma_{kl}.$

To remain consistent with (1), the pressure must then be determined via the equation

$p \ \frac{1}{\kappa} + d = 0, \hspace{4cm} (2)$

where

$d = G^{ij} \gamma_{ij}$

is the generalised dilatation (which reduces to the actual dilatation in the small-strain limit). The inverse bulk modulus is defined as

$\frac{1}{\kappa} = \frac{(1-2\nu)(1+\nu)}{\nu}$

and tends to zero as $\nu \to 0.$ The alternative form of the constitutive equation can therefore be used for any value of $\nu$ . If $\nu = 1/2,$ the constraint (2) enforces i.e incompressible behaviour (at least in the small displacement regime – for large deflections the constraint (2) simply ensures that the generalised dilatation vanishes; this may not be a physically meaningful constraint).

III. Truly incompressible behaviour

Finally, we may retain the decomposition of the stress into its deviatoric and non-deviatoric parts but determine the pressure from the actual incompressibility constraint, i.e. replace (2) by

$\det G_{ij} - \det g_{ij} = 0. \hspace{5cm} (3)$

In this case, the deviatoric part of the stress is determined by the material's constitutive parameters, i.e. its Young's modulus and its Poisson ratio while the pressure (acting as the Lagrange multiplier for the constraint (3)) enforces true incompressibility.

Disclaimer We wish to stress that not all the combinations discussed above are necessarily physically meaningful. For instance, as already acknowledged, setting $\nu = 1/2$ in formulation II does not ensure true incompressibility (in the sense of (3)) if the solid undergoes large deflections. Similarly, setting $\nu$ to a value that differs from

while enforcing true incompressibility via formulation III would be extremely odd. Furthermore, it is not clear (to us) if our generalisation of Hooke's law (obtained by replacing the undeformed metric tensor $g_{ij}$ by its deformed counterpart $G_{ij}$ yields a constitutive equation that is particularly useful for any specific material. However, the same is true for any other constitutive equation – not all of them are useful for all materials! The important point is that all constitutive equations that allow for compressible and incompressible behaviour contain combinations of constitutive parameters that blow up as incompressibility is approached. Formulation II shows how to express such constitutive laws in a way that can be used for any value of the constitutive parameters.

With this disclaimer in mind, we will now demonstrate the use of the various combinations outlined above in a simple test problem for which an exact (linearised) solution is available.

The problem

Here is a sketch of the problem: Three faces of a square elastic body are surrounded by "slippery" rigid walls that allow the body to slide freely along them. The body is subject to a vertical, gravitational body force, acting in the negative -direction.

Sketch of the problem.

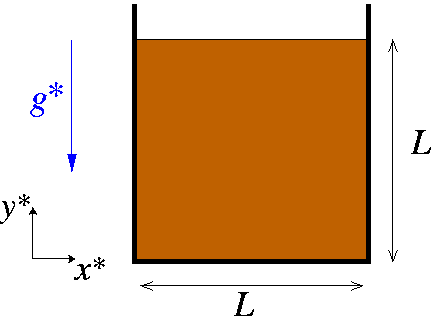
We choose the height of the square as the reference length for the non-dimensionalisation by setting ${\cal L} = L,$ and use the characteristic stiffness associated with the body's constitutive equation to scale the stresses and the body forces. For instance, for linear elastic behaviour, we choose the reference stress to be the solid's Young's modulus, thus setting ${\cal S} = E.$ The non-dimensional body force is then given by ${\bf f} = - g \ {\bf e}_y,$ where

$g = \frac{\rho g^* L}{E}$

indicates the magnitude of the gravitational load relative to the body's stiffness; see the Solid Mechanics Theory Tutorial for full details on the non-dimensionalisation of the governing equations.

An exact solution

Assuming weak loading, i.e. $g \ll 1$ , the body will undergo small deflections and its deformation will be governed by the equations of linear elasticity. Given that the walls bounding the solid are slippery, it is easy to show that a displacement field has the form ${\bf u} = v(y)\ {\bf e}_y$ . Inserting this ansatz into the Navier-Lame equations shows that the non-dimensional displacement in the vertical direction is given by

$v(y) = g \ \frac{(1+\nu)(1-2\nu)}{(1-\nu)} \left( \frac{1}{2} y^2 - y \right).$

The stresses are given by

$\sigma_{xx} = \frac{g \ \nu}{(1-\nu)} (y-1) \ , \ \ \ \ \sigma_{xy} = 0 \ , \mbox{ \ \ \ and \ \ \ } \sigma_{yy} = g \ (y-1) \ .$

This shows that, as the solid approaches incompressibility, $\nu \to 1/2,$ the displacements are suppressed and the stress distribution becomes hydrostatic with $\sigma_{xx} \to \sigma_{yy}.$

Results

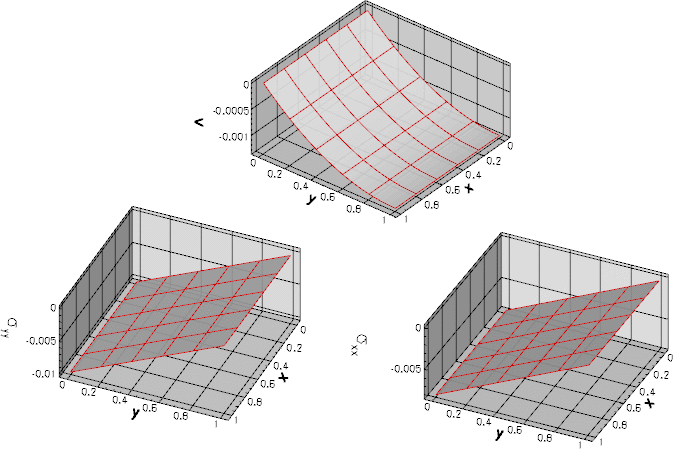
Here is a plot of the three non-zero quantities (the vertical displacement , and the horizontal and vertical stresses, $\sigma_{xx}$ and $\sigma_{yy}$ , respectively) for $g = 10^{-2}$ and $\nu =0.45.$ The shaded surface shows the exact solution while the mesh shows the finite element solution obtained with the displacement formulation of the problem. The solutions obtained with formulations II and III are graphically indistinguishable. All other quantities (the transverse displacement and the shear stress $\sigma_{xy}$ ) are of order $10^{-12}.$

Plot of the vertical displacement and the horizontal and vertical stresses, respectively.

The driver code listed below also computes solutions for various other values of $\nu$ (including the incompressible case $\nu=1/2$ ), and demonstrates how to enforce "true" incompressibility via formulation III. Furthermore, it computes a solution based on the incompressible Mooney-Rivlin constitutive law. The agreement between analytical and computed results is as good as the one shown in the above plot. In particular in all cases where incompressibility is enforced, the vertical displacement is suppressed and the stress state becomes hydrostatic, as predicted by the analytical solution.

Modifying the element's output function

Since we wish to compare the stresses and displacements against the analytical solution, we modify the SolidElement's output function by means of a wrapper class that overloads the SolidElement::output(...).

//=================start_wrapper==================================
/// Wrapper class for solid element to modify the output 
//================================================================
template <class ELEMENT>
class MySolidElement : public virtual ELEMENT
{
 
public:
 
 /// Constructor: Call constructor of underlying element
 MySolidElement() : ELEMENT() {}
 
 /// Overload output function
 void output(std::ostream &outfile, const unsigned &n_plot)
  {
   Vector<double> s(2);
   Vector<double> x(2);
   Vector<double> xi(2);
   DenseMatrix<double> sigma(2,2);
   
   //Tecplot header info 
   outfile << "ZONE I=" << n_plot << ", J=" << n_plot << std::endl;
   
   //Loop over plot points
   for(unsigned l2=0;l2<n_plot;l2++)
    {
     s[1] = -1.0 + l2*2.0/(n_plot-1);
     for(unsigned l1=0;l1<n_plot;l1++)
      {
       s[0] = -1.0 + l1*2.0/(n_plot-1);
       
       // Get Eulerian and Lagrangian coordinates and the stress
       this->interpolated_x(s,x);
       this->interpolated_xi(s,xi);
       this->get_stress(s,sigma);
       
       //Output the x,y coordinates
       for(unsigned i=0;i<2;i++) 
        {outfile << x[i] << " ";}
       
       // Output displacements, the difference between Eulerian and Lagrangian
       // coordinates
       for(unsigned i=0;i<2;i++) 
        {outfile << x[i]-xi[i] << " ";}
       
       //Output stress
       outfile << sigma(0,0) << " "
               << sigma(1,0) << " "
               << sigma(1,1) << " "
               << std::endl;
      }
    }  
  }
};

Problem Parameters

As usual we define the various problem parameters in a global namespace. We prepare a pointer to a constitutive equation and define Poisson's ratio for use with the generalised Hookean constitutive law.

//=======start_namespace==========================================
/// Global variables
//================================================================
namespace Global_Physical_Variables
{
 
 /// Pointer to constitutive law
 ConstitutiveLaw* Constitutive_law_pt=0;
 
 /// Poisson's ratio for Hooke's law
 double Nu=0.45;

We also prepare a pointer to a strain energy function and define the coefficients for the Mooney Rivlin law:

 
 /// Pointer to strain energy function 
 StrainEnergyFunction* Strain_energy_function_pt=0;
 
 /// First "Mooney Rivlin" coefficient for generalised Mooney Rivlin law
 double C1=1.3;
 
 /// Second "Mooney Rivlin" coefficient for generalised Mooney Rivlin law
 double C2=1.3;

Finally, we define the gravitational body force.

 
 /// Non-dim gravity
 double Gravity=0.0;
 
 /// Non-dimensional gravity as body force
 void gravity(const double& time, 
              const Vector<double> &xi,
              Vector<double> &b)
 {
  b[0]=0.0;
  b[1]=-Gravity;
 }
 
} //end namespace

The driver code

The driver code solves the problem with a large number of different formulations and constitutive equations. We start with the generalised Hookean constitutive equation and consider three different values of Poisson's ratio, corresponding to compressible, near-incompressible and incompressible behaviour:

//=======start_of_main==================================================
/// Driver for compressed square
//======================================================================
int main()
{
 
 //Flag to indicate if we want the material to be incompressible 
 bool incompress=false;
 
 // Label for different cases
 int case_number=-1;
 
 // Generalised Hookean constitutive equations
 //===========================================
 {
  // Nu values
  Vector<double> nu_value(3);
  nu_value[0]=0.45;
  nu_value[1]=0.499999;
  nu_value[2]=0.5;
  
  // Loop over nu values
  for (unsigned i=0;i<3;i++)
   {
    // Set Poisson ratio
    Global_Physical_Variables::Nu=nu_value[i];
  
    std::cout << "===========================================\n";
    std::cout << "Doing Nu=" <<  Global_Physical_Variables::Nu 
              << std::endl;
    std::cout << "===========================================\n";
 
    // Create constitutive equation
    Global_Physical_Variables::Constitutive_law_pt = 
     new GeneralisedHookean(&Global_Physical_Variables::Nu);

First, we solve the problem in the pure displacement formulation, using (the wrapped version of the) displacement-based QPVDElements. (As discussed above, the displacement formulation cannot be used for $\nu=1/2$ .)

    
    // Displacement-based formulation
    //--------------------------------
    // (not for nu=1/2, obviously)
    if (i!=2) 
     {
      case_number++;
      std::cout 
       << "Doing Generalised Hookean with displacement formulation: Case "
       << case_number << std::endl;
      
      //Set up the problem with pure displacement based elements
      incompress=false;
      CompressedSquareProblem<MySolidElement<QPVDElement<2,3> > > 
       problem(incompress);
      
      // Run it
      problem.run_it(case_number,incompress);
     }

Next we consider the pressure/displacement formulation with continuous pressures (Taylor-Hood), using the
QPVDElementWithContinuousPressure element.

    
 
    // Generalised Hookean with continuous pressure, compressible
    //-----------------------------------------------------------
    {
     case_number++;
     std::cout 
      << "Doing Generalised Hookean with displacement/cont pressure "
      << "formulation: Case " << case_number << std::endl;     
     
     //Set up the problem with continous pressure/displacement
     incompress=false;
     CompressedSquareProblem<MySolidElement<
      QPVDElementWithContinuousPressure<2> > > 
      problem(incompress); 
     
     // Run it
     problem.run_it(case_number,incompress);
    }

We suppress the listing of the remaining combinations (see the driver code compressed_square.cc for details):

Pressure/displacement formulation with discontinuous pressures (Crouzeix-Raviart), using the QPVDElementWithPressure element.
Pressure/displacement formulation with continuous pressures (Taylor-Hood), using the QPVDElementWithContinuousPressure element, with true incompressibility enforced via formulation III.
Pressure/displacement formulation with discontinuous pressures (Crouzeix-Raviart), using the QPVDElementWithPressure element, with true incompressibility enforced via formulation III.

Before the end of the loop over the different $\nu$ values we delete the constitutive equation, allowing it to be re-built with a different Poisson ratio.

    // Clean up
    delete Global_Physical_Variables::Constitutive_law_pt;
    Global_Physical_Variables::Constitutive_law_pt=0;
    
   } 
 
 } // end generalised Hookean

Next we build the strain-energy-based Mooney-Rivlin constitutive law

 
 
 // Incompressible Mooney Rivlin
 //=============================
 {
 
  // Create strain energy function
  Global_Physical_Variables::Strain_energy_function_pt = 
   new MooneyRivlin(&Global_Physical_Variables::C1,
                    &Global_Physical_Variables::C2);
  
  // Define a constitutive law (based on strain energy function)
  Global_Physical_Variables::Constitutive_law_pt = 
   new IsotropicStrainEnergyFunctionConstitutiveLaw(
    Global_Physical_Variables::Strain_energy_function_pt);

and solve the problem with QPVDElementWithContinuousPressure and QPVDElementWithPressure elements, enforcing true incompressibility enforced via formulation III by setting the incompressible flag to true.

    
 
  // Mooney-Rivlin with continous pressure/displacement; 
  //----------------------------------------------------
  // incompressible
  //---------------
  {
   case_number++;
   std::cout 
    << "Doing Mooney Rivlin with cont pressure formulation: Case "
    << case_number << std::endl; 
   
   //Set up the problem with continous pressure/displacement
   incompress=true;
   CompressedSquareProblem<MySolidElement<
    QPVDElementWithContinuousPressure<2> > > 
    problem(incompress); 
     
   // Run it
   problem.run_it(case_number,incompress);
  }
    
 
  // Mooney-Rivlin with discontinous pressure/displacement; 
  //-------------------------------------------------------
  // incompressible
  //---------------
  {
   case_number++;
   std::cout 
    << "Doing Mooney Rivlin with discont pressure formulation: Case "
    << case_number << std::endl; 
   
   //Set up the problem with discontinous pressure/displacement
   incompress=true;
   CompressedSquareProblem<MySolidElement<
    QPVDElementWithPressure<2> > > 
    problem(incompress); 
     
   // Run it
   problem.run_it(case_number,incompress);
  }
 
 
  // Clean up
  delete  Global_Physical_Variables::Strain_energy_function_pt;
  Global_Physical_Variables::Strain_energy_function_pt=0;
  
  delete Global_Physical_Variables::Constitutive_law_pt;
  Global_Physical_Variables::Constitutive_law_pt=0;
  
 }
   
} //end of main

The Problem class

The Problem class has the usual member functions. The i_case label is used to distinguish different cases while the boolean incompressible indicates if we wish to enforce incompressibility via formulation III.

//=============begin_problem============================================ 
/// Problem class
//====================================================================== 
template<class ELEMENT>
class CompressedSquareProblem : public Problem
{
 
public:
 
 /// Constructor: Pass flag that determines if we want to use
 /// a true incompressible formulation
 CompressedSquareProblem(const bool& incompress);
 
 /// Update function (empty)
 void actions_after_newton_solve() {}
 
 /// Update function (empty)
 void actions_before_newton_solve() {}
 
 /// Doc the solution & exact (linear) solution for compressible 
 /// or incompressible materials
 void doc_solution(const bool& incompress);
 
 /// Run the job -- doc in RESLTi_case
 void run_it(const int& i_case,const bool& incompress);
 
private:
 
 /// Trace file
 ofstream Trace_file;
 
 /// Pointers to node whose position we're tracing
 Node* Trace_node_pt;
 
 /// DocInfo object for output
 DocInfo Doc_info;
 
};

The Problem constructor

We start by building the mesh – the SolidMesh version of the ElasticRectangularQuadMesh.

//===========start_of_constructor======================================= 
/// Constructor: Pass flag that determines if we want to enforce
/// incompressibility
//====================================================================== 
template<class ELEMENT>
CompressedSquareProblem<ELEMENT>::CompressedSquareProblem(
 const bool& incompress)
{
 
 // Create the mesh
 
 // # of elements in x-direction
 unsigned n_x=5;
 
 // # of elements in y-direction
 unsigned n_y=5;
 
 // Domain length in x-direction
 double l_x=1.0;
 
 // Domain length in y-direction
 double l_y=1.0;
 
 //Now create the mesh 
 mesh_pt() = new ElasticRectangularQuadMesh<ELEMENT>(n_x,n_y,l_x,l_y);

We complete the build of the elements by specifying the constitutive equation and the gravitational body force.

 
 
 //Assign the physical properties to the elements
 unsigned n_element=mesh_pt()->nelement();
 for(unsigned i=0;i<n_element;i++)
  {
   //Cast to a solid element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(i));
   
   // Set the constitutive law
   el_pt->constitutive_law_pt() =
    Global_Physical_Variables::Constitutive_law_pt;
 
   //Set the body force
   el_pt->body_force_fct_pt() = Global_Physical_Variables::gravity;

If the element is based on the pressure/displacement form of the principle of virtual displacements we enforce (true) incompressibility if required. Note that, by default, oomph-lib's pressure/displacement-based solid mechanics elements do not assume incompressibility, i.e. the default is to use formulation II.

 
 
   // Is the element based on the pressure/displacement formulation?
   PVDEquationsWithPressure<2>* test_pt = 
    dynamic_cast<PVDEquationsWithPressure<2>*>(mesh_pt()->element_pt(i));
   if (test_pt!=0)
    {
     // Do we want true incompressibility (formulation III in the 
     // associated tutorial) or not (formulation II)
     if (incompress)
      {     
       test_pt->set_incompressible();
      }
     else
      {
       // Note that this assignment isn't strictly necessary as it's the
       // default setting, but it doesn't do any harm to be explicit.
       test_pt->set_compressible();
      }
    }
  } // end compressibility

Finally, we pick a control node to document the solid's load-displacement characteristics and apply the boundary conditions (no displacements normal to the "slippery" walls) before setting up the equation numbering scheme.

 
 
 // Choose a control node: The last node in the solid mesh
 unsigned nnod=mesh_pt()->nnode();
 Trace_node_pt=mesh_pt()->node_pt(nnod-1);
 
// Pin the left and right boundaries (1 and 2) in the horizontal directions
 for (unsigned b=1;b<4;b+=2)
  {
   unsigned nnod = mesh_pt()->nboundary_node(b);
   for(unsigned i=0;i<nnod;i++)
    {
     dynamic_cast<SolidNode*>(
      mesh_pt()->boundary_node_pt(b,i))->pin_position(0);
    }
  }
 
// Pin the bottom boundary (0) in the vertical direction
 unsigned b=0;
 {
  unsigned nnod= mesh_pt()->nboundary_node(b);
  for(unsigned i=0;i<nnod;i++)
   {
    dynamic_cast<SolidNode*>(
     mesh_pt()->boundary_node_pt(b,i))->pin_position(1);
   }
 }
 
 //Assign equation numbers
 assign_eqn_numbers();
 
} //end of constructor

Post-processing

The post-processing routine documents the load-displacement characteristics in a trace file and outputs the deformed domain shape.

 
 
 
//==============start_doc===========================================
/// Doc the solution
//==================================================================
template<class ELEMENT>
void CompressedSquareProblem<ELEMENT>::doc_solution(const bool& incompress)
{
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned n_plot = 5; 
 
 // Output shape of and stress in deformed body
 sprintf(filename,"%s/soln%i.dat",Doc_info.directory().c_str(),
         Doc_info.number());
 some_file.open(filename);
 mesh_pt()->output(some_file,n_plot);
 some_file.close();
 
 // Write trace file: Load/displacement characteristics
 Trace_file << Global_Physical_Variables::Gravity  << " " 
            << Trace_node_pt->x(0) << " " 
            << Trace_node_pt->x(1) << " " 
            << std::endl;

We then output the exact solution of the linearised equations using the same format as in the element's overloaded output function.

 
 
 // Output exact solution for linear elasticity
 // -------------------------------------------
 sprintf(filename,"%s/exact_soln%i.dat",Doc_info.directory().c_str(),
         Doc_info.number());
 some_file.open(filename);
 unsigned nelem=mesh_pt()->nelement(); 
 Vector<double> s(2);
 Vector<double> x(2);
 DenseMatrix<double> sigma(2,2);
 
 // Poisson's ratio
 double nu=Global_Physical_Variables::Nu;
 if (incompress) nu=0.5;
 
 // Loop over all elements
 for (unsigned e=0;e<nelem;e++)
  {  
   //Cast to a solid element
   ELEMENT* el_pt = dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(e));
    
   //Tecplot header info 
   some_file << "ZONE I=" << n_plot << ", J=" << n_plot << std::endl;
   
   //Loop over plot points
   for(unsigned l2=0;l2<n_plot;l2++)
    {
     s[1] = -1.0 + l2*2.0/(n_plot-1);
     for(unsigned l1=0;l1<n_plot;l1++)
      {
       s[0] = -1.0 + l1*2.0/(n_plot-1);
       
       // Get Lagrangian coordinates
         el_pt->interpolated_x(s,x);
 
         // Output the x,y,..
         for(unsigned i=0;i<2;i++) 
          {some_file << x[i] << " ";}
 
         // Exact vertical displacement
         double v_exact=Global_Physical_Variables::Gravity*
          (1.0+nu)*(1.0-2*nu)/(1.0-nu)*(0.5*x[1]*x[1]-x[1]);
         
         // x and y displacement
         some_file << "0.0 " <<   v_exact << " ";
 
         // Stresses
         sigma(0,0)=nu/(1.0-nu)*Global_Physical_Variables::Gravity*(x[1]-1.0);
         sigma(1,0)=0.0;
         sigma(1,1)=Global_Physical_Variables::Gravity*(x[1]-1.0);
          
         // Output linear stress tensor
         some_file << sigma(0,0) << " "
                   << sigma(1,0) << " "
                   << sigma(1,1) << " "
                   << std::endl;
      }
    }
  }
 some_file.close();
 
 // Increment label for output files
 Doc_info.number()++;
 
} //end doc

Comments and Exercises

As usual, oomph-lib provides self-tests that assess if the enforcement incompressibility (or the lack thereof) is consistent:

The compiler will not allow the user to enforce incompressibility on elements that are based on the displacement form of the principle of virtual displacements. This is because the displacement-based elements do not have a member function incompressible().
Certain constitutive laws, such as the Mooney-Rivlin law used in the present example require an incompressible formulation. If oomph-lib is compiled with the PARANOID flag, an error is thrown if such a constitutive law is used by an element for which incompressibility has not been requested.

Recall that the default setting is not to enforce incompressibility!
If the library is compiled without the PARANOID flag no warning will be issued but the results will be "wrong" at least in the sense that the material does not behave like an incompressible Mooney-Rivlin solid. In fact, it is likely that the Newton solver will diverge. Anyway, as we keep saying, without the PARANOID flag, you're on your own!

You should experiment with different combinations of constitutive laws and element types to familiarise yourself with these issues.

Source files for this tutorial

The source files for this tutorial are located in the directory:

demo_drivers/solid/compressed_square/
The driver code is:

demo_drivers/solid/compressed_square/compressed_square.cc

PDF file

A pdf version of this document is available.