Steady Convection Rolls: contours of temperature and element boundaries for a two-dimensional domain heated from below at Ra = 1800

We study convection of an incompressible Newtonian fluid heated from below in a two-dimensional domain of height : the Bénard problem. The lower wall is maintained at a temperature $\theta_{bottom}$ and the upper wall is maintained at a temperature $\theta_{top}$ , where $\theta_{bottom} > \theta_{top}$ . The theory is described the non-refineable version of the problem.

In this example, we solve the same physical problem, but using refineable elements. As an alternative to the time-stepping procedure adopted previously, we perturb the trivial steady-state solution and re-solve the steady equations to obtain the steady symmetry-broken solution. In what follows, we shall only describe those parts of the code that differ from the non-refineable version.

The driver code

We start by setting the direction of gravity, and constructing the problem using the new RefineableBuoyantQCrouzeixRaviartElements, described below.

//===============start_of_main========================================
/// Driver code for 2D Boussinesq convection problem with 
/// adaptivity.
//====================================================================
int main()
{
 
 // Set the direction of gravity
 Global_Physical_Variables::Direction_of_gravity[0] = 0.0;
 Global_Physical_Variables::Direction_of_gravity[1] = -1.0;
 
 // Create the problem with 2D nine-node refineable elements.
 RefineableConvectionProblem<
  RefineableBuoyantQCrouzeixRaviartElement<2> > problem;

As discussed in the previous example, a small perturbation is required to force the solution from the trivial steady state of zero velocity and linear temperature variation. Therefore, we add a small perturbation to the vertical velocity on the upper wall before solving the steady problem, allowing for up to two levels of adaptive mesh refinement.

 
 // Apply a perturbation to the upper boundary condition to
 // force the solution into the symmetry-broken state.
 problem.enable_imperfection();
 
 //Solve the problem with (up to) two levels of adaptation
 problem.newton_solve(2);
 
 //Document the solution
 problem.doc_solution();

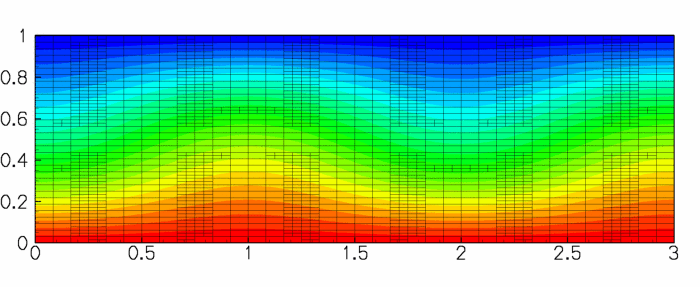
Having forced the solution into a non-trivial symmetry-broken state, we switch off the perturbation and re-solve the problem, allowing for another two levels of adaptive refinement. The Newton solver now converges to the unperturbed but symmetry-broken solution shown above.

 
 // Make the boundary conditions perfect and solve again. 
 // Now the slightly perturbed symmetry broken state computed
 // above is used as the initial condition and the Newton solver
 // converges to the symmetry broken solution, even without
 // the perturbation
 problem.disable_imperfection();
 problem.newton_solve(2);
 problem.doc_solution();
 
} // end of main

The problem class

The problem class contains the constructor and (empty) destructor, the usual action functions, and an access function to the specific mesh used in this problem.

//=======start_of_problem_class=======================================
/// 2D Convection  problem on rectangular domain, discretised 
/// with refineable elements. The specific type
/// of element is specified via the template parameter.
//====================================================================
template<class ELEMENT> 
class RefineableConvectionProblem : public Problem
{
 
public:
 
 /// Constructor
 RefineableConvectionProblem();
 
 /// Destructor. Empty
 ~RefineableConvectionProblem() {}
 
 /// Update the problem specs before solve:
 void actions_before_newton_solve();
 
 /// Update the problem after solve (empty)
 void actions_after_newton_solve(){}
 
 /// Overloaded version of the problem's access function to 
 /// the mesh. Recasts the pointer to the base Mesh object to 
 /// the actual mesh type.
 RectangularQuadMesh<ELEMENT>* mesh_pt() 
  {
   return dynamic_cast<RectangularQuadMesh<ELEMENT>*>(
    Problem::mesh_pt());
  } //end of access function to specic mesh

No specific action is required before the adaptation but following the mesh adaptation exactly one pressure degree of freedom must be pinned in the problem. (Since the domain is enclosed the pressure is only determined up to an arbitrary constant.) The pressure degree of freedom that was pinned before the adaptation may have disappeared during the adaptation, therefore the constraint must be re-applied. However, we unpin all pressure degrees of freedom first to ensure that we do not accidentally pin two pressure degrees of freedom.

 
 /// Actions before adapt:(empty)
 void actions_before_adapt() {}
 
 /// Actions after adaptation,
 /// Re-pin a single pressure degree of freedom
 void actions_after_adapt()
  {
   //Unpin all the pressures to avoid pinning two pressures
   RefineableNavierStokesEquations<2>::
    unpin_all_pressure_dofs(mesh_pt()->element_pt());
 
   //Pin the zero-th pressure dof in the zero-th element and set
   // its value to zero
   fix_pressure(0,0,0.0);
  }
 
 /// Fix pressure in element e at pressure dof pdof and set to pvalue
 void fix_pressure(const unsigned &e, const unsigned &pdof, 
                   const double &pvalue)
  {
   //Cast to specific element and fix pressure
   dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(e))->
    fix_pressure(pdof,pvalue);
  } // end_of_fix_pressure

The remaining member functions provide access to the boolean flag that controls the application of the imperfection, and document the solution:

 
 /// Set the
 /// boundary condition on the upper wall to be perturbed slightly
 /// to force the solution into the symmetry broken state.
 void enable_imperfection() {Imperfect = true;}
 
 /// Set the
 /// boundary condition on the upper wall to be unperturbed.
 void disable_imperfection() {Imperfect = false;}
 
 /// Doc the solution.
 void doc_solution();
 
private:
 
 /// DocInfo object
 DocInfo Doc_info;
 
 /// Is the boundary condition imperfect or not
 bool Imperfect;
 
}; // end of problem class

The constructor

We pass the element type as a template parameter to the problem constructor, which has no arguments. The constructor builds a coarse initial RefineableRectangularQuadMesh, using $9 \times 8$ elements and allocates a spatial error estimator that is attached to the mesh.

//=======start_of_constructor=============================================
/// Constructor for adaptive thermal convection problem
//========================================================================
template<class ELEMENT>
RefineableConvectionProblem<ELEMENT>::
RefineableConvectionProblem() : Imperfect(false)
{ 
 // Set output directory
 Doc_info.set_directory("RESLT");
 
 // # of elements in x-direction
 unsigned n_x=9;
 
 // # of elements in y-direction
 unsigned n_y=8;
 
 // Domain length in x-direction
 double l_x=3.0;
 
 // Domain length in y-direction
 double l_y=1.0;
 
 // Build the mesh
 RefineableRectangularQuadMesh<ELEMENT>* cast_mesh_pt =
  new RefineableRectangularQuadMesh<ELEMENT>(n_x,n_y,l_x,l_y);
 
 //Set the problem's mesh pointer
 Problem::mesh_pt() = cast_mesh_pt;
 
 
 // Create/set error estimator
 cast_mesh_pt->spatial_error_estimator_pt()=new Z2ErrorEstimator;
 
 // Set error targets for adaptive refinement
 cast_mesh_pt->max_permitted_error()=0.5e-3; 
 cast_mesh_pt->min_permitted_error()=0.5e-4; 

Next, the boundary constraints are imposed. We pin all velocities and the temperature on the top and bottom walls and pin only the horizontal velocity on the sidewalls. As discussed above, a single pressure value must be pinned to ensure a unique solution.

 // Set the boundary conditions for this problem: All nodes are
 // free by default -- only need to pin the ones that have Dirichlet 
 // conditions here
 
 //Loop over the boundaries
 unsigned num_bound = mesh_pt()->nboundary();
 for(unsigned ibound=0;ibound<num_bound;ibound++)
  {
   //Set the maximum index to be pinned (all values by default)
   unsigned val_max=3;
   //If we are on the side-walls, the v-velocity and temperature
   //satisfy natural boundary conditions, so we only pin the
   //first value
   if((ibound==1) || (ibound==3)) {val_max=1;}
 
   //Loop over the number of nodes on the boundry
   unsigned num_nod= mesh_pt()->nboundary_node(ibound);
   for (unsigned inod=0;inod<num_nod;inod++)
    {
     //Loop over the desired values stored at the nodes and pin
     for(unsigned j=0;j<val_max;j++)
      {
       mesh_pt()->boundary_node_pt(ibound,inod)->pin(j);
      }
    }
  }
 
 // Pin the zero-th pressure value in the zero-th element and
 // set its value to zero.
 fix_pressure(0,0,0.0);

We complete the build of the elements by setting the pointers to the physical parameters and finally assign the equation numbers

 unsigned n_element = mesh_pt()->nelement();
 for(unsigned i=0;i<n_element;i++)
  {
   // Upcast from GeneralsedElement to the present element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(i));
 
   // Set the Peclet number
   el_pt->pe_pt() = &Global_Physical_Variables::Peclet;
 
   // Set the Peclet Strouhal number
   el_pt->pe_st_pt() = &Global_Physical_Variables::Peclet;
 
   // Set the Reynolds number (1/Pr in our non-dimensionalisation)
   el_pt->re_pt() = &Global_Physical_Variables::Inverse_Prandtl;
 
   // Set ReSt (also 1/Pr in our non-dimensionalisation)
   el_pt->re_st_pt() = &Global_Physical_Variables::Inverse_Prandtl;
 
   // Set the Rayleigh number
   el_pt->ra_pt() = &Global_Physical_Variables::Rayleigh;
 
   //Set Gravity vector
   el_pt->g_pt() = &Global_Physical_Variables::Direction_of_gravity;
  }
 
 // Setup equation numbering scheme
 cout <<"Number of equations: " << assign_eqn_numbers() << endl; 
 
} // end of constructor

The function fix_pressure(...)

This function is a simple wrapper to the element's fix_pressure(...) function.

 /// Fix pressure in element e at pressure dof pdof and set to pvalue
 void fix_pressure(const unsigned &e, const unsigned &pdof, 
                   const double &pvalue)
  {
   //Cast to specific element and fix pressure
   dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(e))->
    fix_pressure(pdof,pvalue);
  } // end_of_fix_pressure

The function actions_before_newton_solve(...)

The function is used to set the specific values of the Dirichlet boundary conditions. If the boolean flag Imperfect is true then a small mass-conserving imperfection is added to the velocity boundary condition on the top wall.

//===================start_actions_before_newton_solve===========================
/// Update the problem specs before solve: (Re-)set boundary conditions
/// to include an imperfection (or not) depending on the control flag.
//========================================================================
template<class ELEMENT>
void RefineableConvectionProblem<ELEMENT>::actions_before_newton_solve()
{
 // Loop over the boundaries
 unsigned num_bound = mesh_pt()->nboundary();
 for(unsigned ibound=0;ibound<num_bound;ibound++)
  {
   // Loop over the nodes on boundary 
   unsigned num_nod=mesh_pt()->nboundary_node(ibound);
   for(unsigned inod=0;inod<num_nod;inod++)
    {
     // Get pointer to node
     Node* nod_pt=mesh_pt()->boundary_node_pt(ibound,inod);
 
     //Set the number of velocity components
     unsigned vel_max=2;
     //If we are on the side walls we only pin the x-velocity.
     if((ibound==1) || (ibound==3)) {vel_max = 1;}
     //Set the pinned velocities to zero
     for(unsigned j=0;j<vel_max;j++) {nod_pt->set_value(j,0.0);}
 
     //If we are on the top boundary
     if(ibound==2) 
      {
       //Set the temperature to -0.5 (cooled)
       nod_pt->set_value(2,-0.5);
       //Add small velocity imperfection if desired
       if(Imperfect)
        {
         //Read out the x position
         double x = nod_pt->x(0);
         //Set a sinusoidal perturbation in the vertical velocity
         //This perturbation is mass conserving
         double value = sin(2.0*3.141592654*x/3.0);
         nod_pt->set_value(1,value);
        }
      }
 
     //If we are on the bottom boundary, set the temperature
     //to 0.5 (heated)
     if(ibound==0) {nod_pt->set_value(2,0.5);}
    }
  }
 
}  // end of actions before solve

The function doc_solution(...)

This function writes the complete velocity, pressure and temperature fields to a file in the output directory specified in the DocInfo object.

//====================start_of_doc_solution===============================
/// Doc the solution
//========================================================================
template<class ELEMENT>
void RefineableConvectionProblem<ELEMENT>::doc_solution()
{ 
 //Declare an output stream and filename
 ofstream some_file;
 char filename[100];
 
 // Number of plot points: npts x npts
 unsigned npts=5;
 
 // Output solution 
 //-----------------
 sprintf(filename,"%s/soln%i.dat",Doc_info.directory().c_str(),
         Doc_info.number());
 some_file.open(filename);
 mesh_pt()->output(some_file,npts);
 some_file.close();
 
 Doc_info.number()++;
} // end of doc

Creating the new RefineableBouyantQCrouzeixRaviartElement class

As in the non-refineable version of the problem we create the refineable element RefineableBuoyantQCrouzeixRaviartElement by multiple inheritance from the RefineableQCrouzeixRaviartElement and RefineableQAdvectionDiffusionElement:

  //============start_element_class============================================
  /// A RefineableElement class that solves the
  /// Boussinesq approximation of the Navier--Stokes
  /// and energy equations by coupling two pre-existing classes.
  /// The RefineableQAdvectionDiffusionElement
  /// with bi-quadratic interpolation for the
  /// scalar variable (temperature) and
  /// RefineableQCrouzeixRaviartElement which solves the Navier--Stokes
  /// equations using bi-quadratic interpolation for the velocities and a
  /// discontinuous bi-linear interpolation for the pressure. Note that we are
  /// free to choose the order in which we store the variables at the nodes. In
  /// this case we choose to store the variables in the order fluid velocities
  /// followed by temperature. We must, therefore, overload the function
  /// AdvectionDiffusionEquations<DIM>::u_index_adv_diff() to indicate that
  /// the temperature is stored at the DIM-th position not the 0-th. We do not
  /// need to overload the corresponding function in the
  /// NavierStokesEquations<DIM> class because the velocities are stored
  /// first. Finally, we choose to use the flux-recovery calculation from the
  /// fluid velocities to provide the error used in the mesh adaptation.
  //==========================================================================
  template<unsigned DIM>
  class RefineableBuoyantQCrouzeixRaviartElement
    : public virtual RefineableQAdvectionDiffusionElement<DIM, 3>,
      public virtual RefineableQCrouzeixRaviartElement<DIM>
  {

Many of the additional member functions required in the combined multi-physics element are identical to those in the non-refineable version:

the access function to (the pointer to the) Rayleigh number, ra_pt(),
the output functions, output(...),
the function required_n_value(...) which specifies the number of values required at each node,
the function u_index_adv_diff(...) which specifies the index at which the temperature is stored within the elements' Nodes,
the function get_wind_adv_diff(...) which specifies the "wind" in the advection diffusion equations in terms of the Navier-Stokes velocities,
the function get_body_force_nst(...) which specifies the body force in the Navier-Stokes equations in terms of the temperature.
the two "fill in" function are implemented as in the non-refineable element. The function fill_in_contribution_to_residuals(...) concatenates the contributions from the two underlying elements; the function fill_in_contribution_to_jacobian(...) computes the coupled elemental Jacobian matrix by finite-differencing.

We shall only discuss those additional functions that are required in the refineable version of the combined multi-physics element.

Both constituent elements are derived from the ElementWithZ2ErrorEstimator base class and each element provides its own definition of the "Z2-flux" that is used by the Z2 error estimator to compute elemental error estimates. We must decide on a single error estimator for the combined element. We could base the error estimation entirely on the fluid flow, or the temperature field, but instead we shall choose our single error estimate to be the maximum of the fluid and temperature error estimates. The functions required by the Z2ErrorEstimator are overloaded to return all the flux terms associated with both the velocity and temperature fields, with the velocity field terms stored first.

    /// The recovery order is that of the NavierStokes elements.
    unsigned nrecovery_order()
    {
      return RefineableQCrouzeixRaviartElement<DIM>::nrecovery_order();
    }
 
    /// The number of Z2 flux terms is the same as that in
    /// the fluid element plus that in the advection-diffusion element
    unsigned num_Z2_flux_terms()
    {
      return (
        RefineableQCrouzeixRaviartElement<DIM>::num_Z2_flux_terms() +
        RefineableQAdvectionDiffusionElement<DIM, 3>::num_Z2_flux_terms());
    }
 
 
    /// Get the Z2 flux by concatenating the fluxes from the fluid and
    /// the advection diffusion elements.
    void get_Z2_flux(const Vector<double>& s, Vector<double>& flux)
    {
      // Find the number of fluid fluxes
      unsigned n_fluid_flux =
        RefineableQCrouzeixRaviartElement<DIM>::num_Z2_flux_terms();
 
      // Fill in the first flux entries as the velocity entries
      RefineableQCrouzeixRaviartElement<DIM>::get_Z2_flux(s, flux);
 
      // Find the number of temperature fluxes
      unsigned n_temp_flux =
        RefineableQAdvectionDiffusionElement<DIM, 3>::num_Z2_flux_terms();
      Vector<double> temp_flux(n_temp_flux);
 
      // Get the temperature flux
      RefineableQAdvectionDiffusionElement<DIM, 3>::get_Z2_flux(s, temp_flux);
 
      // Add the temperature flux to the end of the flux vector
      for (unsigned i = 0; i < n_temp_flux; i++)
      {
        flux[n_fluid_flux + i] = temp_flux[i];
      }
 
    } // end of get_Z2_flux

The default behaviour of the Z2 error estimator is to combine all components of the flux vector into a single compound flux. In the present multi-physics element, we instead define two compound fluxes: one corresponding to the combined temperature fluxes and the other to the combined velocity field fluxes. The flux components associated with each compound flux must specified by overloading the function get_Z2_compound_flux_indices which returns a vector of the same length as the number of flux components, containing the index of the compound flux to which the flux component contributes.

    /// The number of compound fluxes is two (one for the fluid and
    /// one for the temperature)
    unsigned ncompound_fluxes()
    {
      return 2;
    }
 
    /// Fill in which flux components are associated with the fluid
    /// measure and which are associated with the temperature measure
    void get_Z2_compound_flux_indices(Vector<unsigned>& flux_index)
    {
      // Find the number of fluid fluxes
      unsigned n_fluid_flux =
        RefineableQCrouzeixRaviartElement<DIM>::num_Z2_flux_terms();
      // Find the number of temperature fluxes
      unsigned n_temp_flux =
        RefineableQAdvectionDiffusionElement<DIM, 3>::num_Z2_flux_terms();
 
      // The fluid fluxes are first
      // The values of the flux_index vector are zero on entry, so we
      // could omit this line
      for (unsigned i = 0; i < n_fluid_flux; i++)
      {
        flux_index[i] = 0;
      }
 
      // Set the temperature fluxes (the last set of fluxes
      for (unsigned i = 0; i < n_temp_flux; i++)
      {
        flux_index[n_fluid_flux + i] = 1;
      }
 
    } // end of get_Z2_compound_flux_indices

The Z2ErrorEstimator calculates the error estimates for each compound flux. The individual error estimates are then combined to a single error estimate by the function Z2ErrorEstimator::get_combined_error_estimate(). By default the single error estimate is chosen to be the maximum of all calculated error estimates. Alternative user-defined functions can be specified via the function pointer Z2ErrorEstimator::CombinedErrorEstimateFctPt& combined_error_fct_pt(), see Comments for a more detailed discussion of this aspect.

The vertex nodes are defined by the underlying geometric element, but require a final overload to prevent ambiguities:

    /// Number of vertex nodes in the element is obtained from the
    /// geometric element.
    unsigned nvertex_node() const
    {
      return QElement<DIM, 3>::nvertex_node();
    }

    /// Pointer to the j-th vertex node in the element,
    /// Call the geometric element's function.
    Node* vertex_node_pt(const unsigned& j) const
    {
      return QElement<DIM, 3>::vertex_node_pt(j);
    }

The number of continuously interpolated values is DIM + 1: DIM velocity components and one temperature.

    unsigned ncont_interpolated_values() const
    {
      return DIM + 1;
    }

The two versions of the get_interpolated_values(...) function must return the continuously interpolated variables at a specified position within the element:

    /// Get the continuously interpolated values at the local coordinate
    /// s. We choose to put the fluid velocities first, followed by the
    /// temperature.
    void get_interpolated_values(const Vector<double>& s,
                                 Vector<double>& values)
    {
      // Storage for the fluid velocities
      Vector<double> nst_values;
 
      // Get the fluid velocities from the fluid element
      RefineableQCrouzeixRaviartElement<DIM>::get_interpolated_values(
        s, nst_values);
 
      // Storage for the temperature
      Vector<double> advection_values;
 
      // Get the temperature from the advection-diffusion element
      RefineableQAdvectionDiffusionElement<DIM, 3>::get_interpolated_values(
        s, advection_values);
 
      // Add the fluid velocities to the values vector
      for (unsigned i = 0; i < DIM; i++)
      {
        values.push_back(nst_values[i]);
      }
 
      // Add the concentration to the end
      values.push_back(advection_values[0]);
    }
 
 
    /// Get all continuously interpolated values at the local
    /// coordinate s at time level t (t=0: present; t>0: previous).
    /// We choose to put the fluid velocities first, followed by the
    /// temperature
    void get_interpolated_values(const unsigned& t,
                                 const Vector<double>& s,
                                 Vector<double>& values)
    {
      // Storage for the fluid velocities
      Vector<double> nst_values;
 
      // Get the fluid velocities from the fluid element
      RefineableQCrouzeixRaviartElement<DIM>::get_interpolated_values(
        t, s, nst_values);
 
      // Storage for the temperature
      Vector<double> advection_values;
 
      // Get the temperature from the advection-diffusion element
      RefineableQAdvectionDiffusionElement<DIM, 3>::get_interpolated_values(
        s, advection_values);
 
      // Add the fluid velocities to the values vector
      for (unsigned i = 0; i < DIM; i++)
      {
        values.push_back(nst_values[i]);
      }
 
      // Add the concentration to the end
      values.push_back(advection_values[0]);
 
    } // end of get_interpolated_values

Finally, the setup and build functions must call the build functions of the two constituent elements. In addition, the pointer to the Rayleigh number must be passed to the sons after refinement.

    /// The additional hanging node information must be set up
    /// for both single-physics elements.
    void further_setup_hanging_nodes()
    {
      RefineableQCrouzeixRaviartElement<DIM>::further_setup_hanging_nodes();
      RefineableQAdvectionDiffusionElement<DIM,
                                           3>::further_setup_hanging_nodes();
    }
 
 
    /// Call the rebuild_from_sons functions for each of the
    /// constituent multi-physics elements.
    void rebuild_from_sons(Mesh*& mesh_pt)
    {
      RefineableQAdvectionDiffusionElement<DIM, 3>::rebuild_from_sons(mesh_pt);
      RefineableQCrouzeixRaviartElement<DIM>::rebuild_from_sons(mesh_pt);
    }
 
 
    /// Call the underlying single-physics element's further_build()
    /// functions and make sure that the pointer to the Rayleigh number
    /// is passed to the sons
    void further_build()
    {
      RefineableQCrouzeixRaviartElement<DIM>::further_build();
      RefineableQAdvectionDiffusionElement<DIM, 3>::further_build();
 
      // Cast the pointer to the father element to the specific
      // element type
      RefineableBuoyantQCrouzeixRaviartElement<DIM>* cast_father_element_pt =
        dynamic_cast<RefineableBuoyantQCrouzeixRaviartElement<DIM>*>(
          this->father_element_pt());
 
      // Set the pointer to the Rayleigh number to be the same as that in
      // the father
      this->Ra_pt = cast_father_element_pt->ra_pt();
    } // end of further build

Comments and Exercises

Comments

Error estimation for multi-physics elements

The error estimation for the combined multi-physics element is performed with the Z2ErrorEstimator which computes an error estimate based Zienkiewicz and Zhu's flux recovery technique, using the elemental "Z2 flux" defined in the pure virtual function get_Z2_flux(...). The two constituent elements already provide their own implementation of this function:
- In the RefineableQAdvectionDiffusionElement the temperature gradient is used as the flux.
- In the RefineableQCrouzeixRaviartElement the flux is defined by the components of the fluid's rate of strain tensor.
It is not obvious what combination of these flux terms should be used to compute the error estimates for the combined multi-physics element. The most general option would be to combine the two flux vectors, possibly using a weighting factor to control the relative importance of the various components.

In the example above, we chose an error estimate that was the maximum value of the individual error estimates for the Navier-Stokes flux and the temperature flux. Refinement will be performed if either of the single-physics error estimates are above the chosen thresholds. It is also possible to base the error estimation entirely on the Navier-Stokes fluxes; an appropriate choice for problems in which the variations in the velocity field are expected to be much more rapid than those in the temperature field. Alternatively,
the error estimation could be based exclusively on the temperature field; a choice that would be appropriate for problems with thin thermal boundary layers. The different error estimates can all be specified by user-defined functions that combine the vector of compound-flux error estimates into a single number. For example, the function
double navier_stokes_flux_error(const Vector<double> &errors)

{return errors[0];}

specifies that the combined error estimate is the first of the compound error estimates — the error estimate for the Navier–Stokes equations.

In the current example both fields vary very smoothly, and as a result spatial adaptivity is not really required in this problem. This is why we set a very narrow range of target errors – if the default targets are used, oomph-lib refines the mesh uniformly.

Exercises

Confirm that for a Rayleigh number of 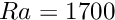the system is stable, i.e. it returns to the trivial state, when the perturbation to the vertical velocity on the upper wall is switched off.
Re-write the multi-physics elements so that the temperature is stored before the fluid velocities. Confirm that the solution is unchanged in this case.
Try using RefineableQTaylorHoodElements as the "fluid" element part of the multi-physics elements.
Change the error estimate to be based entirely on the error in the Navier–Stokes fluxes by using a user-defined function. Is there any difference in the refinement pattern?

Source files for this tutorial

The source files for this tutorial are located in the directory:

demo_drivers/multi_physics/boussinesq_convection/
The driver code is:

demo_drivers/multi_physics/boussinesq_convection/boussinesq_convection.cc
The source code for the elements is in:

src/multi_physics/boussinesq_elements.h

PDF file

A pdf version of this document is available.