Parallel solution of Turek & Hron's FSI benchmark problem with spatial adaptivity for the fluid and solid meshes

This document provides an overview of

  • how to distribute the problem across multiple processors,

and

  • how to enable load balancing of the problem once it is distributed.

The document is part of a series of tutorials that discuss how to modify existing serial driver codes so that the Problem object can be distributed across multiple processors.

Enabling spatial adaptivity for the fluid and solid meshes

In the original (serial) driver code for Turek & Hron's FSI benchmark problem we only adapted the fluid mesh. Before discussing how to modify the code to refine the fluid and solid meshes simultaneously, we provide a brief reminder of the procedure used to discretise fluid-structure interaction problems that involve fluid and solid domains of equal spatial dimension (e.g. a 2D fluid domain interacting with a 2D solid domain) when using algebraic node update methods to adjust the position of the nodes in the fluid mesh.
We refer to another tutorial for a discussion of FSI problems involving the interaction of fluids with (lower-dimensional) shell and beam structures.

General methodology

The figure below shows a sketch of a simple(r) fluid-structure interaction problem involving fluid and solid domains that meet along a single mesh boundary. We assume that the fluid mesh uses an algebraic node update function to adjust the position of its nodes in response to changes in the domain boundary, represented by the GeomObject shown in magenta. (You may wish to consult another tutorial for a reminder of how oomph-lib's algebraic node update methods work).

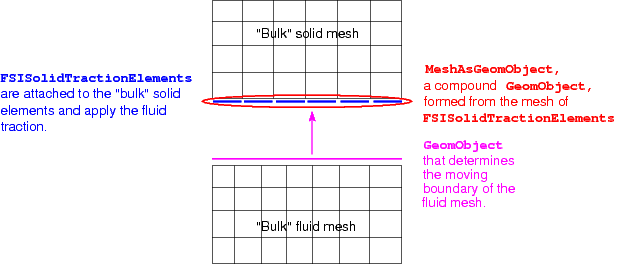
Basic setup for FSI problems involving algebraic node updates for the fluid mesh.

In an FSI problem, the fluid mesh's free boundary is a boundary of the solid mesh, i.e. the boundary along which the fluid exerts a traction onto the solid. Within oomph-lib, the fluid traction is applied to the solid domain by attaching FSISolidTractionElements to the faces of the "bulk" solid elements adjacent to the FSI boundary. (In the above sketch the FSISolidTractionElements are shown in blue.) The deformation of the fluid and solid meshes is coupled by using the MeshAsGeomObject formed from the FSISolidTractionElements as the GeomObject that defines the moving boundary of the fluid mesh. (In sketch above, this is indicated by the magenta arrow.)

Modifications to allow adaptivity of the fluid and solid meshes

If the solid mesh is not adapted, the adaptation for the fluid mesh is straightforward and proceeds fully automatically as described elsewhere. In particular, the node update data for newly-created fluid nodes is created automatically by a call to the AlgebraicMesh::update_node_update(...) function during the adaptation. This function obtains the required information about the boundary by using the MeshAsGeomObject built from the FSISolidTractionElements.

If the solid mesh is also adapted, then the existing FSISolidTractionElements must (at some point) be deleted and new ones must be attached to the adapted "bulk" solid mesh. In all other problems, this is done by deleting the FSISolidTractionElements in Problem::actions_before_adapt() and attaching new ones in Problem::actions_after_adapt(); see, e.g. the tutorial on the solution of a Poisson problem with flux boundary conditions. However, in the present problem this is not possible because, once the FSISolidTractionElements have been deleted, the MeshAsGeomObject can no longer be used to represent the shape and position of the FSI boundary, which would cause the adaptation of the fluid mesh to fail.

To avoid this problem, we adopt the following strategy:

  1. When adding the various meshes to the Problem's collection of sub-meshes, we add the fluid mesh before the solid mesh. (This happens to be what was done already in the original driver code.) Usually, the order in which sub-meshes are added to the Problem is irrelevant. Here the order does matter because we will exploit the fact that the sub-meshes are adapted individually, in the order in which they were added to the Problem.

  2. The FSISolidTractionElements are not deleted in Problem::actions_before_adapt() and remain attached to the "bulk" solid elements throughout the "bulk" mesh adaptation procedure. When the fluid mesh is adapted, the appropriate MeshAsGeomObject is, therefore, still fully-functional (and refers to the boundary as represented by the solid domain before the "bulk" solid mesh is adapted).

    Here is a sketch of problem after adaptation of the fluid mesh:

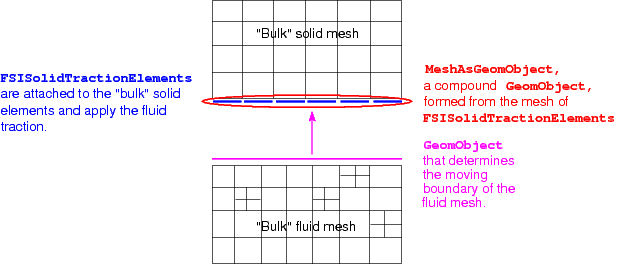    Sketch of the problem following the adaptation of the fluid mesh. The solid mesh has not yet been refined.


  3. The subsequent adaptation of the "bulk" solid mesh is likely to turn some of the FSISolidTractionElements into "dangling" elements. (This occurs whenever a FSISolidTractionElements is attached to a "bulk" solid elements that disappears during the adaptation, e.g. by being refined.)

    Here is a plot of the problem following the adaptation of the solid mesh :

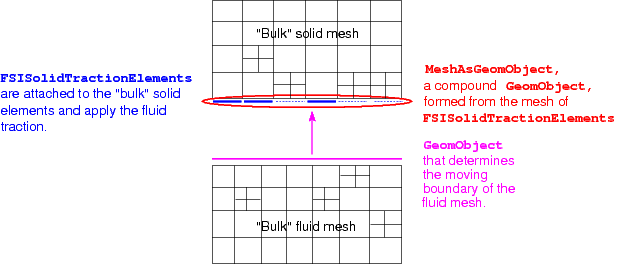    Sketch of the problem following the adaptation of the solid mesh -- the `dangling' FSISolidTractionElements are represented by dotted lines.


  4. Hence, in Problem::actions_after_adapt() we delete the existing FSISolidTractionElements and immediately (re-)attach new ones. Now, the MeshAsGeomObject that represents the FSI boundary is broken because it still refers to the just deleted FSISolidTractionElements.

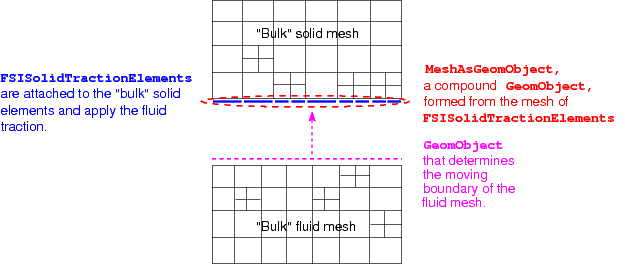    Sketch of the problem following the creation of new FSISolidTractionElements. The fact that the MeshAsGeomObject is broken is indicated by the dashed lines.


  5. Thus, we rebuild the MeshAsGeomObject from the newly-created FSISolidTractionElements, and update the fluid mesh's pointer to this new GeomObject that describes the boundary shape.

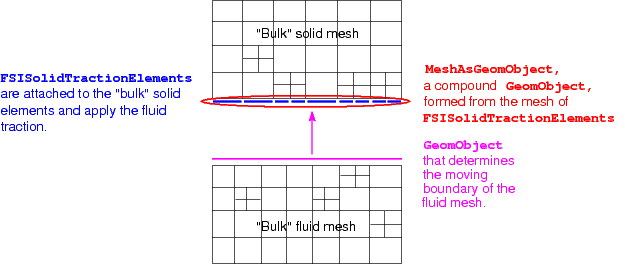    Sketch of the problem with re-built MeshAsGeomObject.


  6. Finally, we execute the AlgebraicMesh::update_node_update(...) function for all nodes in the fluid mesh to ensure that their node update data refers to the new FSISolidTractionElements.

  7. The remaining tasks (such as the renewed setup of the fluid load on the FSISolidTractionElements via a call to FSI_functions::setup_fluid_load_info_for_solid_elements(...), etc.) remain the same as in the previous version of the code.

Distributing the Problem

In the present example, there are two "bulk" meshes corresponding to the fluid and solid domains and three "surface" meshes of traction elements. The traction elements are FaceElements created from the "bulk" fluid elements and should be deleted before the problem is distributed, see the tutorial on applying flux boundary conditions in a Poisson problem for more details. In the previous example involving the interaction of a 2D fluid domain with a 1D beam structure there were only two meshes: a "bulk" fluid mesh and a "surface" solid mesh. In that problem all elements in the 1D mesh of FSIHermiteBeamElements were retained on all processors as halo elements by using the function Mesh::keep_all_elements_as_halos(). The same methodology could be used here, but it would be extremely wasteful to retain all the solid elements in the "bulk" solid mesh because only the elements next to the FSI boundary are required. Instead, we use a more fine-grained method of retaining elements via the function GeneralisedElement::must_be_kept_as_halo().

Implementation

Most of the driver code is identical to the original serial version discussed in another tutorial. We therefore only discuss those parts of the code that have to be changed to allow (i) the simultaneous adaptation of the fluid and solid meshes, and (ii) the problem distribution.

The main function

As usual in a parallel driver code, the only addition to the main() function is the inclusion of calls to MPI_Helpers::init(), MPI_Helpers::finalize(), and the Problem::distribute() functions.

The problem class

The only additions to the serial version of the problem class are the functions actions_before_distribute() and actions_after_distribute(), and the helper function delete_fsi_traction_elements(), discussed below.

Deleting the FSISolidTractionElements

To facilitate the deletion and re-creation of the FSISolidTractionElements before and after the adaptation (and distribution) we provide a new helper function delete_fsi_traction_elements() which complements the already-existing create_fsi_traction_elements() function:

//============start_of_delete_traction_elements==========================
/// Delete FSI traction elements
//=======================================================================
template<class FLUID_ELEMENT,class SOLID_ELEMENT >
void TurekProblem<FLUID_ELEMENT,SOLID_ELEMENT>::delete_fsi_traction_elements()
{
// There are 3 traction meshes
for (unsigned b=0;b<3;b++)
{
unsigned n_element=Traction_mesh_pt[b]->nelement();
for (unsigned e=0;e<n_element;e++)
{
// Kill the element
delete Traction_mesh_pt[b]->element_pt(e);
}
// Wipe the mesh
Traction_mesh_pt[b]->flush_element_and_node_storage();
}
} // end of delete traction elements

Actions before distribute

As discussed above, we must ensure that the "bulk" solid elements adjacent to the FSI boundary are retained on all processors. Hence, the actions_before_distribute() function starts with a loop over the FSISolidTractionElements within which we use the function GeneralisedElement::must_be_kept_as_halo() to indicate that the associated bulk elements must be retained.

//==================start_of_actions_before_distribute====================
/// Actions before distribute: Make sure that the bulk solid elements
/// attached to the FSISolidTractionElements are kept as halo elements.
/// Unlike in most other parallel codes we DON'T delete the
/// FSISolidTractionElements here, though, because they need to
/// be around while the fluid mesh is adapted.
//========================================================================
template<class FLUID_ELEMENT,class SOLID_ELEMENT >
void TurekProblem<FLUID_ELEMENT,SOLID_ELEMENT>::actions_before_distribute()
{
// The bulk elements attached to the traction elements need to be kept
// as halo elements
// There are 3 traction meshes
for (unsigned b=0;b<3;b++)
{
// Loop over elements in traction meshes
unsigned n_element=Traction_mesh_pt[b]->nelement();
for (unsigned e=0;e<n_element;e++)
{
FSISolidTractionElement<SOLID_ELEMENT,2>* traction_elem_pt=
dynamic_cast<FSISolidTractionElement<SOLID_ELEMENT,2>* >
(Traction_mesh_pt[b]->element_pt(e));
// Get the bulk element (which is a SOLID_ELEMENT)
SOLID_ELEMENT* solid_elem_pt = dynamic_cast<SOLID_ELEMENT*>
(traction_elem_pt->bulk_element_pt());
// Require bulk to be kept as a (possible) halo element
// Note: The traction element itself will "become" a halo element
// when it is recreated after the distribution has taken place
solid_elem_pt->set_must_be_kept_as_halo();
}
} // end of loop over meshes of fsi traction elements

Next, we flush all the meshes from the problem's collection of sub-meshes and add only the "bulk" fluid and solid meshes (in that order!). The FaceElements do not need to be distributed, because they will be re-created in actions_after_distribute().

// Flush all the submeshes out but keep the meshes of FSISolidTractionElements
// alive (i.e. don't delete them)
flush_sub_meshes();
// Add the fluid mesh and the solid mesh back again
// Remember that it's important that the fluid mesh is
// added before the solid mesh!
add_sub_mesh(fluid_mesh_pt());
add_sub_mesh(solid_mesh_pt());
// Rebuild global mesh
rebuild_global_mesh();
} // end of actions before distribute

Actions after distribute

Following the problem distribution, we delete the old FSISolidTractionElements and then (re-)attach new ones, which will be created as halo elements where necessary.

//==================start_of_actions_after_distribute=====================
/// Actions after distribute: Re-setup FSI
//========================================================================
template<class FLUID_ELEMENT,class SOLID_ELEMENT >
void TurekProblem<FLUID_ELEMENT,SOLID_ELEMENT>::actions_after_distribute()
{
// The solid mesh has now been distributed, so it now has halo elements
// on certain processors. The traction elements attached to these new
// halo elements need to be halo themselves, so we need to delete the
// old ones and re-attach new ones. Recall that FaceElements attached
// to bulk halo elements become halos themselves.
delete_fsi_traction_elements();
// (Re-)Build the FSI traction elements
create_fsi_traction_elements();

We complete the build of the FSISolidTractionElements by passing the FSI parameter and the boundary number in the bulk mesh. The relevant code is identical to the serial version and we omit its listing here.

Next, we create new MeshAsGeomObjects from the newly-created FSISolidTractionElements and pass them to the (algebraic) fluid mesh:

// Turn the three meshes of FSI traction elements into compound
// geometric objects (one Lagrangian, two Eulerian coordinates)
// that determine particular boundaries of the fluid mesh
MeshAsGeomObject*
bottom_flag_pt=
new MeshAsGeomObject
(Traction_mesh_pt[0]);
MeshAsGeomObject* tip_flag_pt=
new MeshAsGeomObject
(Traction_mesh_pt[1]);
MeshAsGeomObject* top_flag_pt=
new MeshAsGeomObject
(Traction_mesh_pt[2]);
// Delete the old MeshAsGeomObjects and tell the fluid mesh
// about the new ones.
delete fluid_mesh_pt()->bottom_flag_pt();
fluid_mesh_pt()->set_bottom_flag_pt(bottom_flag_pt);
delete fluid_mesh_pt()->top_flag_pt();
fluid_mesh_pt()->set_top_flag_pt(top_flag_pt);
delete fluid_mesh_pt()->tip_flag_pt();
fluid_mesh_pt()->set_tip_flag_pt(tip_flag_pt);

The MeshAsGeomObjects have changed, so we must call the update_node_update() function again for each node in the fluid mesh:

// Call update_node_update for all the fluid mesh nodes, as the
// geometric objects representing the fluid mesh boundaries have changed
unsigned n_fluid_node=fluid_mesh_pt()->nnode();
for (unsigned n=0;n<n_fluid_node;n++)
{
// Get the (algebraic) node
AlgebraicNode* alg_nod_pt=dynamic_cast<AlgebraicNode*>
(fluid_mesh_pt()->node_pt(n));
// Call update_node_update for this node
fluid_mesh_pt()->update_node_update(alg_nod_pt);
}

Now we add the FSI traction meshes back to the problem and rebuild the global mesh.

// Add the traction meshes back to the problem
for (unsigned i=0;i<3;i++)
{
add_sub_mesh(traction_mesh_pt(i));
}
// Rebuild global mesh
rebuild_global_mesh();

Finally, we re-set the fluid load on the solid elements by calling FSI_functions::setup_fluid_load_info_for_solid_elements(...) before re-assigning the auxiliary node update function that imposes the no-slip condition for all fluid nodes on the FSI boundaries. [Recall that the (re-)assignment of the auxiliary node-update function must be performed after the call to FSI_functions::setup_fluid_load_info_for_solid_elements(...).]

// If the solid is to be loaded by the fluid, then set up the interaction
// and specify the velocity of the fluid nodes based on the wall motion
if (!Global_Parameters::Ignore_fluid_loading)
{
#ifdef OLD_FSI
// Re-setup the fluid load information for fsi solid traction elements
FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
(this,5,Fluid_mesh_pt,Traction_mesh_pt[0]);
FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
(this,6,Fluid_mesh_pt,Traction_mesh_pt[2]);
FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
(this,7,Fluid_mesh_pt,Traction_mesh_pt[1]);
#else
// Package fsi solid traction meshes and boundary IDs in
// fluid mesh
Vector<unsigned> fluid_fsi_boundary_id(3);
Vector<Mesh*> traction_mesh_pt(3);
fluid_fsi_boundary_id[0]=5;
traction_mesh_pt[0]=Traction_mesh_pt[0];
fluid_fsi_boundary_id[1]=6;
traction_mesh_pt[1]=Traction_mesh_pt[2];
fluid_fsi_boundary_id[2]=7;
traction_mesh_pt[2]=Traction_mesh_pt[1];
// Vector based FSI setup
FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
(this,fluid_fsi_boundary_id,Fluid_mesh_pt,
traction_mesh_pt);
#endif
// The velocity of the fluid nodes on the wall (fluid mesh boundary 5,6,7)
// is set by the wall motion -- hence the no-slip condition must be
// re-applied whenever a node update is performed for these nodes.
// Such tasks may be performed automatically by the auxiliary node update
// function specified by a function pointer:
for(unsigned ibound=5;ibound<8;ibound++ )
{
unsigned num_nod= Fluid_mesh_pt->nboundary_node(ibound);
for (unsigned inod=0;inod<num_nod;inod++)
{
Fluid_mesh_pt->boundary_node_pt(ibound, inod)->
set_auxiliary_node_update_fct_pt(
FSI_functions::apply_no_slip_on_moving_wall);
}
}
} // end of (re-)assignment of the auxiliary node update fct

The remainder of the function identifies which processors contain the fluid control node whose velocities we document in the trace file.

Actions after adapt

The actions_after_adapt() function is very similar to actions_after_distribute() function, so we omit is listing here. The only significant differences are that (i) the redundant fluid and solid pressures are (re)-pinned; (ii) the identification of the fluid control node does not need to be setup; and (iii) the traction meshes were never removed from the problem, so do not need to be added back in.

The doc_solution() function

As with the other parallel driver codes, the main modification to the post-processing function is the addition of the processor number to all output files. Furthermore, we only write the trace file on the processors that contain the fluid control node. In the interest of brevity we omit the listing of the modified function.

Results

The figure below illustrates the distribution of the problem across four processors, represented by the four colours, with the fluid elements outlined in black and the solid elements outlined in white.

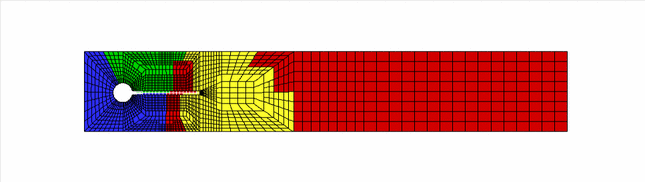
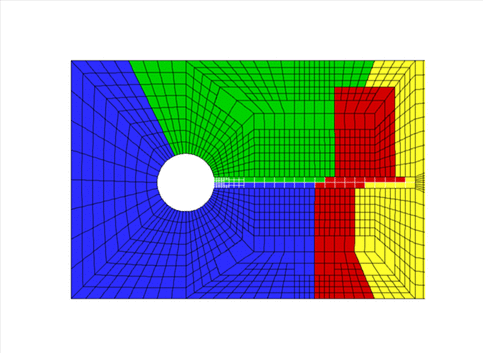
Distribution of the Turek & Hron benchmark problem over four processors.

Zooming in near the "flag" shows how both fluid and solid meshes are refined and distributed independently:

Distribution of the Turek & Hron benchmark problem over four processors; zoomed in view near the `flag'.

Load balancing

When employing load balancing in this problem, we modify the time-stepping loop to perform the procedure after each timestep:

// Start of timestepping loop
for(unsigned i=0;i<nstep;i++)
{
// Solve the problem
problem.unsteady_newton_solve(dt,max_adapt,first);
// Output the solution
problem.doc_solution(doc_info,trace_file);
// Step number
doc_info.number()++;
// Load balance the problem
DocInfo load_doc_info;
problem.load_balance(load_doc_info,report_stats);
} // end of timestepping loop

The build_mesh() function

The function Problem::build_mesh() must be supplied by the user if they wish to use the load balancing capability. Thus, in this driver code, we move all the required code to build the entire global mesh into this function, and call it from within the problem constructor:

//=====start_of_constructor=============================================
/// Constructor: Pass length and height of domain
//======================================================================
template< class FLUID_ELEMENT,class SOLID_ELEMENT >
TurekProblem<FLUID_ELEMENT,SOLID_ELEMENT>::
TurekProblem(const double &length,
const double &height) : Domain_height(height),
Domain_length(length)
{
// Tell us how well the load balancing is doing...
enable_doc_imbalance_in_parallel_assembly();
// Increase max. number of iterations in Newton solver to
// accomodate possible poor initial guesses
Max_newton_iterations=20;
Max_residuals=1.0e4;
// Create the flag timestepper (consistent with BDF<2> for fluid)
Flag_time_stepper_pt=new Newmark<2>;
add_time_stepper_pt(Flag_time_stepper_pt);
// Create error estimator for the solid mesh
Solid_error_estimator_pt=new Z2ErrorEstimator;
//Create a new Circle object as the central cylinder
Cylinder_pt = new Circle(Global_Parameters::Centre_x,
Global_Parameters::Centre_y,
Global_Parameters::Radius);
// Allocate the fluid timestepper
Fluid_time_stepper_pt=new BDF<2>;
add_time_stepper_pt(Fluid_time_stepper_pt);
// Create error estimator for the fluid mesh
Fluid_error_estimator_pt=new Z2ErrorEstimator;
// Build the meshes for this problem
build_mesh();
// Setup FSI
//----------
// Pass Strouhal number to the helper function that automatically applies
// the no-slip condition
FSI_functions::Strouhal_for_no_slip=Global_Parameters::St;
// If the solid is to be loaded by the fluid, then set up the interaction
// and specify the velocity of the fluid nodes based on the wall motion
if (!Global_Parameters::Ignore_fluid_loading)
{
// Work out which fluid dofs affect the residuals of the wall elements:
// We pass the boundary between the fluid and solid meshes and
// pointers to the meshes. The interaction boundary are boundaries 5,6,7
// of the 2D fluid mesh.
FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
(this,5,Fluid_mesh_pt,Traction_mesh_pt[0]);
FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
(this,6,Fluid_mesh_pt,Traction_mesh_pt[2]);
FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
(this,7,Fluid_mesh_pt,Traction_mesh_pt[1]);
// The velocity of the fluid nodes on the wall (fluid mesh boundary 5,6,7)
// is set by the wall motion -- hence the no-slip condition must be
// re-applied whenever a node update is performed for these nodes.
// Such tasks may be performed automatically by the auxiliary node update
// function specified by a function pointer:
for(unsigned ibound=5;ibound<8;ibound++ )
{
unsigned num_nod= Fluid_mesh_pt->nboundary_node(ibound);
for (unsigned inod=0;inod<num_nod;inod++)
{
Fluid_mesh_pt->boundary_node_pt(ibound, inod)->
set_auxiliary_node_update_fct_pt(
FSI_functions::apply_no_slip_on_moving_wall);
}
} // done automatic application of no-slip
} // end of FSI setup
// Use SuperLU_dist as the solver
linear_solver_pt() = new SuperLUSolver;
static_cast<SuperLUSolver*>(linear_solver_pt())
->set_solver_type(SuperLUSolver::Distributed);
static_cast<SuperLUSolver*>(linear_solver_pt())
->use_distributed_solve_in_superlu_dist();
// Assign equation numbers
cout << assign_eqn_numbers() << std::endl;
}//end_of_constructor

The build_mesh() function itself contains all the relevant code from within the previous parallel driver code's problem constructor.

Actions before and after load balancing

In this example, all that is required for the actions_after_load_balance() function is the addition of the unpin-repin procedure from the actions_after_adapt() function to the appropriate part of the actions_after_distribute() function, since all the other functionality is already identical. The actions_before_load_balance() function is identical to the actions_before_distribute() function.

Source files for this tutorial

PDF file

A pdf version of this document is available.