In this example we consider the flow in a 2D channel past a cylinder with an attached elastic "flag". This is the FSI benchmark problem proposed by Turek & Hron,

"Proposal for Numerical Benchmarking of Fluid-Structure Interaction between an Elastic Object and a Laminar Incompressible Flow", S. Turek & J. Hron, pp. 371-385. In: "Fluid-Structure Interaction" Springer Lecture Notes in Computational Science and Engineering 53. Ed. H.-J. Bungartz & M. Schaefer. Springer Verlag 2006.

The problem combines the two single-physics problems of

This is our first example problem that involves the coupling between a fluid and "proper" solid (rather than beam structure) and also includes both fluid and wall inertia.

The problem presented here was used as one of the test cases for oomph-lib's FSI preconditioner; see

Heil, M., Hazel, A.L. & Boyle, J. (2008): Solvers for large-displacement fluid-structure interaction problems: Segregated vs. monolithic approaches. Computational Mechanics.

In this tutorial we concentrate on the problem formulation. The application of the preconditioner is discussed elsewhere – the required source code is contained in the driver code.

The Problem

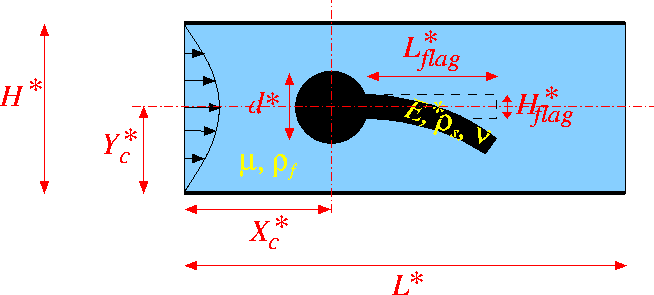
The figure below shows a sketch of the problem: A 2D channel of height and length conveys fluid of density $\rho_f$ and dynamic viscosity $\mu$ and contains a cylinder of diameter , centred at to which a linearly elastic "flag" of thickness $H^*_{flag}$ and length $L^*_{flag}$ is attached. Steady Poiseuille flow with average velocity is imposed at the left end of the channel while we assume the outflow to be parallel and axially traction-free. We model the flag as a linearly elastic Hookean solid with elastic modulus , density $\rho_s$ and Poisson's ratio $\nu.$

Sketch of the problem in dimensional variables.

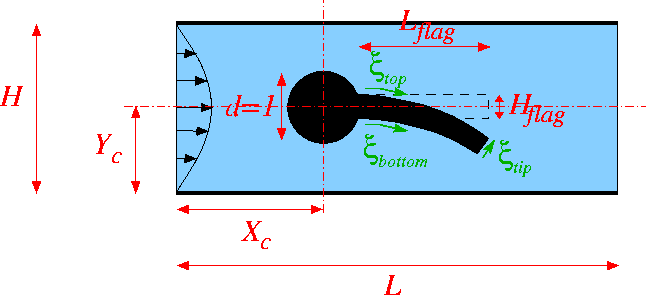
We non-dimensionalise all length and coordinates on the diameter of the cylinder, , the velocities on the mean velocity, , and the fluid pressure on the viscous scale. To facilitate comparisons with Turek & Hron's dimensional benchmark data (particularly for the period of the self-excited oscillations), we use a timescale of $T^* = 1 \ \mbox{sec}$ to non-dimensionalise time. The fluid flow is then governed by the non-dimensional Navier-Stokes equations

$Re \left( St \frac{\partial u_i}{\partial t} + u_j \frac{\partial u_i}{\partial x_j} \right) = - \frac{\partial p}{\partial x_i} + \frac{\partial }{\partial x_j} \left[ \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) \right],$

where $Re = \rho U^* H_0^* / \mu$ and , and

$\frac{\partial u_i}{\partial x_i} = 0,$

subject to parabolic inflow

${\bf u} = 6 x_2 (1-x_2) {\bf e}_1$

at the inflow cross-section; parallel, axially-traction-free outflow at the outlet; and no-slip on the stationary channel walls and the surface of the cylinder, ${\bf u} = {\bf 0}$ . The no-slip condition on the moving flag is

${\bf u} = St \ \frac{\partial {\bf R}_w(\xi_{[top,tip,bottom]},t)}{\partial t} \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)$

where $\xi_{[top,tip,bottom]}$ are Lagrangian coordinates parametrising the three faces of the flag.

We describe the deformation of the elastic flag by the non-dimensional position vector ${\bf R}(\xi^1, \xi^2, t)$ which is determined by the principle of virtual displacements

$\int_{v} \left\{ \sigma^{ij} \ \delta \gamma_{ij} - \left( {\bf f} - \Lambda^2 \frac{\partial^2 {\bf R}}{\partial t^{2}} \right) \cdot \delta {\bf R} \right\} \ dv -\oint_{A_{tract}} {\bf t} \cdot \delta {\bf R} \ dA =0, \ \ \ \ \ \ \ \ (2)$

where all solid stresses and tractions have been non-dimensionalised on Young's modulus, ; see the Solid Mechanics Tutorial for details. The solid mechanics timescale ratio (the ratio of the timescale chosen to non-dimensionalise time, to the intrinsic timescale of the solid) can be expressed in terms of the Reynolds and Strouhal numbers, the density ratio, and the FSI interaction parameter as

$\Lambda^2 = \left( \frac{d^*}{T^*} \sqrt{\frac{\rho_s}{E^*}} \right)^2 = St^2 \left( \frac{\rho_s}{\rho_f} \right) Re \ Q.$

Here is a sketch of the non-dimensional version of the problem:

Sketch of the fluid problem in dimensionless variables, showing the Lagrangian coordinates that parametrise the three faces of the flag.

Parameter values for the benchmark problems

The (dimensional) parameter values given in Turek & Hron's benchmark correspond to the following non-dimensional parameters:

Geometry

Cylinder diameter
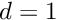
Centre of cylinder
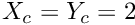
Channel length
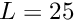
Channel width
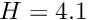
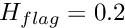
Thickness of the undeformed flag $H_{flag} = 0.2$
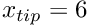
Right end of undeformed flag $x_{tip} = 6$

Non-dimensional parameters

The three FSI test cases correspond to the following non-dimensional parameters:

..	$Re = U^* d^* \rho_f/\mu$	$Q = \mu U^* / (E^* d^*)$	$\rho_s/\rho_f$	$\Lambda^2 = (d^* /T^* \sqrt{\rho_s/E^*})^2 = St^2 (\rho_s/\rho_f) Re \ Q$
FSI1		$1.429 \times 10^{-6}$		$7.145 \times 10^{-6}$
FSI2		$7.143 \times 10^{-6}$		$7.143 \times 10^{-6}$
FSI3		$3.571 \times 10^{-6}$		$1.786 \times 10^{-6}$

Results

The test cases FSI2 and FSI3 are the most interesting because the system develops large-amplitude self-excited oscillations

FSI2

Following an initial transient period the system settles into large-amplitude self-excited oscillations during which the oscillating flag generates a regular vortex pattern that is advected along the channel. This is illustrated in the figure below which shows a snapshot of the flow field (pressure contours and instantaneous streamlines) at

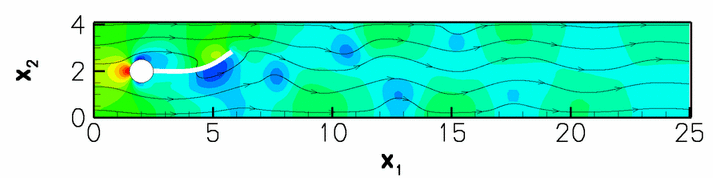
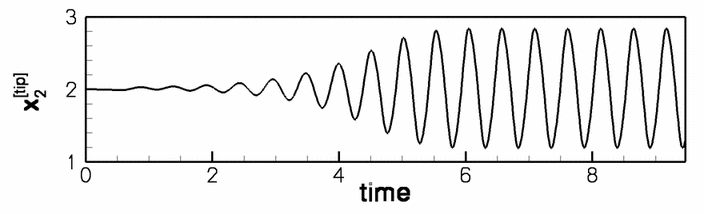
Snapshot of the flow field (instantaneous streamlines and pressure contours)

The constantly adapted mesh contains and average of 65,000 degrees of freedom. A relatively large timestep of $\Delta t = 0.01$ – corresponding to about 50 timesteps per period of the oscillation – was used in this computation. With this discretisation the system settles into oscillations with a period of $\approx 0.52$ and an amplitude of the tip-displacement of $0.01 \pm 0.83.$

Time trace of the tip displacement.

FSI3

The figures below shows the corresponding results for the case FSI3 in which the fluid and solid densities are equal and the Reynolds number twice as large as in the FSI2 case. The system performs oscillations of much higher frequency and smaller amplitude. This is illustrated in the figure below which shows a snapshot of the flow field (pressure contours and instantaneous streamlines) at

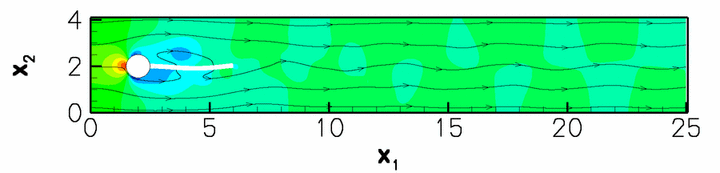
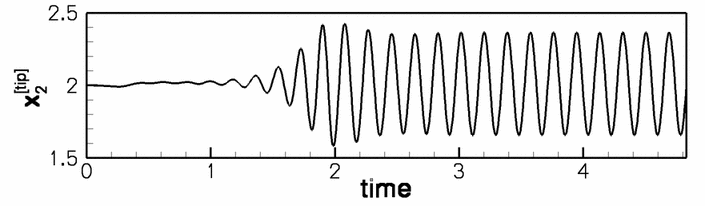
Snapshot of the flow field (instantaneous streamlines and pressure contours)

This computation was performed with a timestep of $\Delta t = 0.005$ and resulted in oscillations with a period of $\approx 0.19$ and an amplitude of the tip-displacement of $0.01 \pm 0.36.$

The increase in frequency and Reynolds number leads to the development of thinner boundary and shear layers which require a finer spatial resolution, involving an average of 84,000 degrees of freedom.

Time trace of the tip displacement.

Overview of the driver code

Since the driver code is somewhat lengthy we start by providing a brief overview of the main steps in the Problem construction:

We start by discretising the flag with 2D solid elements, as in the corresponding single-physics solid mechanics example.
Next we attach FSISolidTractionElements to the three solid mesh boundaries that are exposed to the fluid traction. These elements are used to compute and impose the fluid traction onto the solid elements, using the flow field from the adjacent fluid elements.
We now combine the three sets of FSISolidTractionElements into three individual (sub-)meshes and convert these to GeomObjects, using the MeshAsGeomObject class.
The GeomObject representation of the three surface meshes is then passed to the constructor of the fluid mesh. The algebraic node-update methodology provided in the AlgebraicMesh base class is used to update its nodal positions in response to the motion of its bounding GeomObjects.
Finally, we use the helper function FSI_functions::setup_fluid_load_info_for_solid_elements(...) to set up the fluid-structure interaction – this function determines which fluid elements are adjacent to the Gauss points in the FSISolidTractionElements that apply the fluid traction to the solid.
Done!

Parameter values for the benchmark problems

As usual, We use a namespace to define the (many) global parameters, using default assignments for the FSI1 test case.

//=====start_of_global_parameters=================================
/// Global variables
//================================================================
namespace Global_Parameters
{
 
 /// Default case ID
 string Case_ID="FSI1";
 
 /// Reynolds number (default assignment for FSI1 test case)
 double Re=20.0; 
 
 /// Strouhal number (default assignment for FSI1 test case)
 double St=0.5;
 
 /// Product of Reynolds and Strouhal numbers (default
 /// assignment for FSI1 test case)
 double ReSt=10.0;
 
 /// FSI parameter (default assignment for FSI1 test case)
 double Q=1.429e-6;
 
 /// Density ratio (solid to fluid; default assignment for FSI1
 /// test case)
 double Density_ratio=1.0; 
 
 /// Height of flag
 double H=0.2;
 
 /// x position of centre of cylinder
 double Centre_x=2.0;
 
 /// y position of centre of cylinder
 double Centre_y=2.0;
 
 /// Radius of cylinder
 double Radius=0.5;
 
 /// Pointer to constitutive law
 ConstitutiveLaw* Constitutive_law_pt=0;
 
 /// Timescale ratio for solid (dependent parameter
 /// assigned in set_parameters())
 double Lambda_sq=0.0;
 
 /// Timestep
 double Dt=0.1;
 
 /// Ignore fluid (default assignment for FSI1 test case)
 bool Ignore_fluid_loading=false;
 
 /// Elastic modulus
 double E=1.0;
 
 /// Poisson's ratio
 double Nu=0.4; 

We also include a gravitational body force for the solid. (This is only used for the solid mechanics test cases, CSM1 and CSM2, which will not be discussed here.)

 
 /// Non-dim gravity (default assignment for FSI1 test case)
 double Gravity=0.0; 
 
 /// Non-dimensional gravity as body force
 void gravity(const double& time, 
              const Vector<double> &xi,
              Vector<double> &b)
 {
  b[0]=0.0;
  b[1]=-Gravity;
 }

The domain geometry and flow field are fairly complex and it is difficult to construct a good initial guess for the Newton iteration. To ensure its convergence at the beginning of the simulation we therefore employ the method suggested by Turek & Hron: We start the flow from rest and ramp up the inflow profile from zero to its maximum value. The parameters for the time-dependent increase in the influx are defined here:

 
 /// Period for ramping up in flux
 double Ramp_period=2.0;
 
 /// Min. flux 
 double Min_flux=0.0; 
 
 /// Max. flux
 double Max_flux=1.0;
 
 /// Flux increases between Min_flux and Max_flux over 
 /// period Ramp_period
 double flux(const double& t)
 {    
  if (t<Ramp_period)
   {
    return Min_flux+(Max_flux-Min_flux)*
     0.5*(1.0-cos(MathematicalConstants::Pi*t/Ramp_period));
   }
  else
   {
    return Max_flux;
   }
 } // end of specification of ramped influx

Finally, we provide a helper function that assigns the parameters for the various test cases, depending on their ID ("FSI1", "FSI2", "FSI3", "CSM1" or "CSM2"). Here is the assignment for the case FSI1:

 
 
 /// Set parameters for the various test cases
 void set_parameters(const string& case_id)
 {
 
  // Remember which case we're dealing with
  Case_ID=case_id;
 
  // Setup independent parameters depending on test case
  if (case_id=="FSI1")
   {
    // Reynolds number based on diameter of cylinder
    Re=20.0;
 
    // Strouhal number based on timescale of one second
    St=0.5;
 
    // Womersley number
    ReSt=Re*St;
 
    // FSI parameter
    Q=1.429e-6;
    
    // Timestep -- aiming for about 40 steps per period
    Dt=0.1;
 
    // Density ratio
    Density_ratio=1.0;
 
    // Gravity
    Gravity=0.0;
    
    // Max. flux
    Max_flux=1.0;
 
    // Ignore fluid
    Ignore_fluid_loading=false;
 
    // Compute dependent parameters
    
    // Timescale ratio for solid 
    Lambda_sq=Re*Q*Density_ratio*St*St;
  }

In the interest of brevity we omit the listings of the assignments for the other cases. Finally, we select the length of the time interval over which the influx is ramped up from zero to its maximum value to be equal to 20 timesteps, create a constitutive equation for the solid, and document the parameter values used in the simulation:

  // Ramp period (20 timesteps)
  Ramp_period=Dt*20.0;
 
  // "Big G" Linear constitutive equations:
  Constitutive_law_pt = new GeneralisedHookean(&Nu,&E);
  
  // Doc
  oomph_info << std::endl;
  oomph_info << "-------------------------------------------" 
             << std::endl;
  oomph_info << "Case: " << case_id << std::endl;
  oomph_info << "Re            = " << Re << std::endl;
  oomph_info << "St            = " << St << std::endl;
  oomph_info << "ReSt          = " << ReSt << std::endl;
  oomph_info << "Q             = " << Q << std::endl;
  oomph_info << "Dt            = " << Dt << std::endl;
  oomph_info << "Ramp_period   = " << Ramp_period << std::endl;
  oomph_info << "Max_flux      = " << Max_flux << std::endl;
  oomph_info << "Density_ratio = " << Density_ratio << std::endl;
  oomph_info << "Lambda_sq     = " << Lambda_sq << std::endl;
  oomph_info << "Gravity       = " << Gravity << std::endl;
  oomph_info << "Ignore fluid  = " << Ignore_fluid_loading<< std::endl;
  oomph_info << "-------------------------------------------"
             << std::endl << std::endl;
 }
 
}// end_of_namespace

The driver code

The driver code has the usual structure, though in this case we use the command line arguments to indicate which case (FSI1, FSI2, FSI3, CSM1 or CSM2) to run. The absence of a command line argument is interpreted as the code being run as part of oomph-lib's self-test procedure in which case we perform a computation with the parameter values for case FSI1 and perform only a few timesteps.

//=======start_of_main==================================================
/// Driver 
//======================================================================
int main(int argc, char* argv[])
{
 // Store command line arguments
 CommandLineArgs::setup(argc,argv);
 
 // Get case id as string
 string case_id="FSI1";
 if (CommandLineArgs::Argc==1)
  {
   oomph_info << "No command line arguments; running self-test FSI1" 
              << std::endl;
  }
 else if (CommandLineArgs::Argc==2)
  {
   case_id=CommandLineArgs::Argv[1];
  }
 else
  {
   oomph_info << "Wrong number of command line arguments" << std::endl;
   oomph_info << "Enter none (for default) or one (namely the case id" 
              << std::endl;
   oomph_info << "which should be one of: FSI1, FSI2, FSI3, CSM1" 
              << std::endl;
  } 
 std::cout << "Running case " << case_id << std::endl;

We set up the global parameter values, create a DocInfo object and trace file to record the output, and build the problem.

 
 // Setup parameters for case identified by command line
 // argument
 Global_Parameters::set_parameters(case_id);
 
 // Prepare output
 DocInfo doc_info;
 ofstream trace_file; 
 doc_info.set_directory("RESLT");
 trace_file.open("RESLT/trace.dat");
 
 // Length and height of domain
 double length=25.0;
 double height=4.1;
 
 //Set up the problem
 TurekProblem<AlgebraicElement<RefineableQTaylorHoodElement<2> >,
  RefineableQPVDElement<2,3> > problem(length, height);

Next, we choose the number of timesteps (using a smaller number for a validation run, and for the case FSI1 in which the system rapidly approaches a steady state) and initialise the time-stepping for an impulsive start from the zero flow solution.

 
 // Default number of timesteps
 unsigned nstep=4000;
 if (Global_Parameters::Case_ID=="FSI1")
  {
   std::cout << "Reducing number of steps for FSI1 " << std::endl;
   nstep=400;
  }
 
 if (CommandLineArgs::Argc==1)
  {
   std::cout << "Reducing number of steps for validation " << std::endl;
   nstep=2;
  }
 
 //Timestep: 
 double dt=Global_Parameters::Dt;
 
 // Initialise timestep 
 problem.initialise_dt(dt);
 
 // Impulsive start
 problem.assign_initial_values_impulsive(dt);

Finally, we document the initial condition and start the time-stepping procedure, setting the first flag to false because we have not specified an analytical expression for the initial conditions that could be re-assigned after the mesh adaptation when computing the first timestep.

 
 // Doc the initial condition
 problem.doc_solution(doc_info,trace_file);
 doc_info.number()++; 
 
 // Don't re-set the initial conditions when adapting during first
 // timestep
 bool first = false;
 
 // Max number of adaptation for time-stepping
 unsigned max_adapt=1;
 
 for(unsigned i=0;i<nstep;i++)
  { 
  // Solve the problem
  problem.unsteady_newton_solve(dt,max_adapt,first); 
  
  // Output the solution
  problem.doc_solution(doc_info,trace_file);
  
  // Step number
  doc_info.number()++;
 }
 
 trace_file.close(); 
 
}//end of main

The Problem class

The Problem class contains the usual member functions, such as access functions to the various meshes. Because the nodal positions are updated by an algebraic node-update procedure, the function actions_before_newton_convergence_check() is employed to update the nodal positions in response to changes in the (solid) variables during the Newton iteration. The function actions_before_implicit_timestep() is used to adjust the influx during the start-up period.

//====start_of_problem_class=========================================== 
/// Problem class
//====================================================================== 
template< class FLUID_ELEMENT,class SOLID_ELEMENT >
class TurekProblem : public Problem
{
 
public:
 
 /// Constructor: Pass length and height of domain
 TurekProblem(const double &length, const double &height);
 
 /// Access function for the fluid mesh 
 RefineableAlgebraicCylinderWithFlagMesh<FLUID_ELEMENT>* fluid_mesh_pt() 
  { return Fluid_mesh_pt;}
 
 /// Access function for the solid mesh
 ElasticRefineableRectangularQuadMesh<SOLID_ELEMENT>*& solid_mesh_pt() 
  {return Solid_mesh_pt;} 
 
 /// Access function for the i-th mesh of FSI traction elements
 SolidMesh*& traction_mesh_pt(const unsigned& i)
  {return Traction_mesh_pt[i];} 
 
 /// Actions after adapt: Re-setup the fsi lookup scheme
 void actions_after_adapt();
 
 /// Doc the solution
 void doc_solution(DocInfo& doc_info, ofstream& trace_file);
 
 /// Update function (empty)
 void actions_after_newton_solve() {}
 
 /// Update function (empty)
 void actions_before_newton_solve(){}
 
 /// Update the (dependent) fluid node positions following the
 /// update of the solid variables before performing Newton convergence
 /// check
 void actions_before_newton_convergence_check();
 
 /// Update the time-dependent influx
 void actions_before_implicit_timestep();
 
private:
 
 /// Create FSI traction elements
 void create_fsi_traction_elements();
 
 /// Pointer to solid mesh
 ElasticRefineableRectangularQuadMesh<SOLID_ELEMENT>* Solid_mesh_pt;
 
 /// Pointer to fluid mesh
 RefineableAlgebraicCylinderWithFlagMesh<FLUID_ELEMENT>* Fluid_mesh_pt;
 
 /// Vector of pointers to mesh of FSI traction elements
 Vector<SolidMesh*> Traction_mesh_pt;
 
 /// Combined mesh of traction elements -- only used for documentation
 SolidMesh* Combined_traction_mesh_pt;
 
 /// Overall height of domain
 double Domain_height;
 
 /// Overall length of domain
 double Domain_length;
 
 /// Pointer to solid control node
 Node* Solid_control_node_pt;
 
 /// Pointer to fluid control node
 Node* Fluid_control_node_pt;
 
};// end_of_problem_class

The problem constructor

We start by building the solid mesh, using an initial discretisation with 20 x 2 elements in the x- and y-directions. (The length of the flag is determined such that it emanates from its intersection with the cylinder and ends at x=6; The origin vector shifts the "lower left" vertex of the solid mesh so that its centreline is aligned with the cylinder.)

//=====start_of_constructor============================================= 
/// Constructor: Pass length and height of domain
//====================================================================== 
template< class FLUID_ELEMENT,class SOLID_ELEMENT >
TurekProblem<FLUID_ELEMENT,SOLID_ELEMENT>::
TurekProblem(const double &length,
             const double &height) :  Domain_height(height),
                                      Domain_length(length)
 
{
 // Increase max. number of iterations in Newton solver to
 // accomodate possible poor initial guesses
 Max_newton_iterations=20;
 Max_residuals=1.0e4;
 
 // Build solid mesh
 //------------------
 
 // # of elements in x-direction
 unsigned n_x=20;
 
 // # of elements in y-direction
 unsigned n_y=2;
 
 // Domain length in y-direction 
 double l_y=Global_Parameters::H;
 
 // Create the flag timestepper (consistent with BDF<2> for fluid)
 Newmark<2>* flag_time_stepper_pt=new Newmark<2>;
 add_time_stepper_pt(flag_time_stepper_pt); 
 
 /// Left point on centreline of flag so that the top and bottom
 /// vertices merge with the cylinder.
 Vector<double> origin(2);
 origin[0]=Global_Parameters::Centre_x+
  Global_Parameters::Radius*
  sqrt(1.0-Global_Parameters::H*Global_Parameters::H/
       (4.0*Global_Parameters::Radius*Global_Parameters::Radius));
 origin[1]=Global_Parameters::Centre_y-0.5*l_y;
 
 // Set length of flag so that endpoint actually stretches all the
 // way to x=6:
 double l_x=6.0-origin[0];
 
 //Now create the mesh
 solid_mesh_pt() = new ElasticRefineableRectangularQuadMesh<SOLID_ELEMENT>(
  n_x,n_y,l_x,l_y,origin,flag_time_stepper_pt);

We create an error estimator for the solid mesh and identify a control node at the tip of the flag to track its motion.

 
 // Set error estimator for the solid mesh
 Z2ErrorEstimator* solid_error_estimator_pt=new Z2ErrorEstimator;
 solid_mesh_pt()->spatial_error_estimator_pt()=solid_error_estimator_pt;
 
 
 // Element that contains the control point
 FiniteElement* el_pt=solid_mesh_pt()->finite_element_pt(n_x*n_y/2-1);
 
 // How many nodes does it have?
 unsigned nnod=el_pt->nnode();
 
 // Get the control node
 Solid_control_node_pt=el_pt->node_pt(nnod-1);
 
 std::cout << "Coordinates of solid control point " 
           << Solid_control_node_pt->x(0) << " " 
           << Solid_control_node_pt->x(1) << " " << std::endl;

Finally, we perform one uniform mesh refinement and disable any further mesh adaptation.

 
 // Refine the mesh uniformly
 solid_mesh_pt()->refine_uniformly();
 
 //Do not allow the solid mesh to be refined again
 solid_mesh_pt()->disable_adaptation();

Next, we attach FSISolidTractionElements to the boundaries of the solid mesh that are exposed to the fluid. We complete their build by specifying which boundary of the bulk mesh they are attached to, as this information is required when setting up the fluid-structure interaction; see Further comments and exercises.

 
 
 // Build mesh of solid traction elements that apply the fluid
 //------------------------------------------------------------
 // traction to the solid elements
 //-------------------------------
 
 // Create storage for Meshes of FSI traction elements at the bottom
 // top and left boundaries of the flag
 Traction_mesh_pt.resize(3);
 
 // Now construct the traction element meshes
 Traction_mesh_pt[0]=new SolidMesh;
 Traction_mesh_pt[1]=new SolidMesh;
 Traction_mesh_pt[2]=new SolidMesh;
 
 // Build the FSI traction elements
 create_fsi_traction_elements();
 
 // Loop over traction elements, pass the FSI parameter and tell them 
 // the boundary number in the bulk solid mesh -- this is required so 
 // they can get access to the boundary coordinates!
 for (unsigned bound=0;bound<3;bound++)
  {
   unsigned n_face_element = Traction_mesh_pt[bound]->nelement();
   for(unsigned e=0;e<n_face_element;e++)
    {
     //Cast the element pointer and specify boundary number
     FSISolidTractionElement<SOLID_ELEMENT,2>* elem_pt=
     dynamic_cast<FSISolidTractionElement<SOLID_ELEMENT,2>*>
      (Traction_mesh_pt[bound]->element_pt(e));
 
     // Specify boundary number
     elem_pt->set_boundary_number_in_bulk_mesh(bound);
 
     // Function that specifies the load ratios
     elem_pt->q_pt() = &Global_Parameters::Q;
    
    }
  } // build of FSISolidTractionElements is complete

Finally, we create GeomObject representations of the three surface meshes of FSISolidTractionElements. We will use these to represent the curvilinear, moving boundaries of the fluid mesh.

 
 
 // Turn the three meshes of FSI traction elements into compound
 // geometric objects (one Lagrangian, two Eulerian coordinates)
 // that determine the boundary of the fluid mesh
 MeshAsGeomObject*
  bottom_flag_pt=
  new MeshAsGeomObject
  (Traction_mesh_pt[0]);
 
 MeshAsGeomObject* tip_flag_pt=
  new MeshAsGeomObject
  (Traction_mesh_pt[1]);
 
 MeshAsGeomObject* top_flag_pt=
  new MeshAsGeomObject
  (Traction_mesh_pt[2]);

The final mesh to be built is the fluid mesh whose constructor requires pointers to the four GeomObjects that represent the cylinder and three fluid-loaded faces of the flag, respectively. We represent the cylinder by a Circle object:

 
 
 // Build fluid mesh
 //-----------------
 
 //Create a new Circle object as the central cylinder
 Circle* cylinder_pt = new Circle(Global_Parameters::Centre_x,
                                  Global_Parameters::Centre_y,
                                  Global_Parameters::Radius);

We build the mesh and identify a control node (a node at the upstream face of the cylinder), before creating an error estimator and performing one uniform mesh refinement.

 
 // Allocate the fluid timestepper
 BDF<2>* fluid_time_stepper_pt=new BDF<2>;
 add_time_stepper_pt(fluid_time_stepper_pt);
 
 // Build fluid mesh
 Fluid_mesh_pt=
  new RefineableAlgebraicCylinderWithFlagMesh<FLUID_ELEMENT>
  (cylinder_pt, 
   top_flag_pt,
   bottom_flag_pt,
   tip_flag_pt,
   length, height, 
   l_x,Global_Parameters::H,
   Global_Parameters::Centre_x,
   Global_Parameters::Centre_y,
   Global_Parameters::Radius,
   fluid_time_stepper_pt);
 
 
 // I happen to have found out by inspection that
 // node 5 in the hand-coded fluid mesh is at the 
 // upstream tip of the cylinder
 Fluid_control_node_pt=Fluid_mesh_pt->node_pt(5);
 
 // Set error estimator for the fluid mesh
 Z2ErrorEstimator* fluid_error_estimator_pt=new Z2ErrorEstimator;
 fluid_mesh_pt()->spatial_error_estimator_pt()=fluid_error_estimator_pt;
 
 // Refine uniformly
 Fluid_mesh_pt->refine_uniformly();

We now add the various meshes to the Problem's collection of sub-meshes and combine them to a global mesh

 
 
 // Build combined global mesh
 //---------------------------
 
 // Add Solid mesh the problem's collection of submeshes
 add_sub_mesh(solid_mesh_pt());
 
 // Add traction sub-meshes
 for (unsigned i=0;i<3;i++)
  {
   add_sub_mesh(traction_mesh_pt(i));
  }
 
 // Add fluid mesh
 add_sub_mesh(fluid_mesh_pt());
 
 // Build combined "global" mesh
 build_global_mesh();

The application of boundary conditions for the solid are straightforward: All displacements of the flag's left end (mesh boundary 3) are suppressed; the other faces are free. Strictly speaking, the pinning of the redundant solid pressure nodes is superfluous since the RefineableQPVDElement used for the discretisation of the flag employ a displacement-based formulation, but it is good practise to perform this step anyway to "future-proof" the code for the use of other element types.

 
 
 
 // Apply solid boundary conditons
 //-------------------------------
 
 //Solid mesh: Pin the left boundary (boundary 3) in both directions
 unsigned n_side = mesh_pt()->nboundary_node(3);
 
 //Loop over the nodes
 for(unsigned i=0;i<n_side;i++)
  {
   solid_mesh_pt()->boundary_node_pt(3,i)->pin_position(0);
   solid_mesh_pt()->boundary_node_pt(3,i)->pin_position(1);
  }
 
 // Pin the redundant solid pressures (if any)
 PVDEquationsBase<2>::pin_redundant_nodal_solid_pressures(
  solid_mesh_pt()->element_pt());

The fluid has Dirichlet boundary conditions (prescribed velocity) everywhere apart from the outflow where only the horizontal velocity is unknown.

 
 // Apply fluid boundary conditions
 //--------------------------------
 
 //Fluid mesh: Horizontal, traction-free outflow; pinned elsewhere
 unsigned num_bound = fluid_mesh_pt()->nboundary();
 for(unsigned ibound=0;ibound<num_bound;ibound++)
  {
   unsigned num_nod= fluid_mesh_pt()->nboundary_node(ibound);
   for (unsigned inod=0;inod<num_nod;inod++)
    {
     // Parallel, axially traction free outflow at downstream end
     if (ibound != 1)
      {
       fluid_mesh_pt()->boundary_node_pt(ibound,inod)->pin(0);
       fluid_mesh_pt()->boundary_node_pt(ibound,inod)->pin(1);
      }
     else
      {
       fluid_mesh_pt()->boundary_node_pt(ibound,inod)->pin(1);
      }
    }
  }//end_of_pin
 
 // Pin redundant pressure dofs in fluid mesh
 RefineableNavierStokesEquations<2>::
  pin_redundant_nodal_pressures(fluid_mesh_pt()->element_pt());

We impose a parabolic inflow profile with the current value of the influx at the inlet (fluid mesh boundary 3).

 
 
 // Apply boundary conditions for fluid
 //-------------------------------------
 
 // Impose parabolic flow along boundary 3
 // Current flow rate
 double t=0.0;
 double ampl=Global_Parameters::flux(t);
 unsigned ibound=3; 
 unsigned num_nod= Fluid_mesh_pt->nboundary_node(ibound);
 for (unsigned inod=0;inod<num_nod;inod++)
  {
   double ycoord = Fluid_mesh_pt->boundary_node_pt(ibound,inod)->x(1); 
   double uy = ampl*6.0*ycoord/Domain_height*(1.0-ycoord/Domain_height);
   Fluid_mesh_pt->boundary_node_pt(ibound,inod)->set_value(0,uy);
   Fluid_mesh_pt->boundary_node_pt(ibound,inod)->set_value(1,0.0);    
  }

We complete the build of the solid elements by passing them the pointer to the constitutive equation, the gravity vector and the timescale ratio:

 
 
 // Complete build of solid elements
 //---------------------------------
 
 //Pass problem parameters to solid elements
 unsigned  n_element =solid_mesh_pt()->nelement();
 for(unsigned i=0;i<n_element;i++)
  {
   //Cast to a solid element
   SOLID_ELEMENT *el_pt = dynamic_cast<SOLID_ELEMENT*>(
    solid_mesh_pt()->element_pt(i));
   
   // Set the constitutive law
   el_pt->constitutive_law_pt() =
    Global_Parameters::Constitutive_law_pt;
   
   //Set the body force
   el_pt->body_force_fct_pt() = Global_Parameters::gravity;
 
   // Timescale ratio for solid
   el_pt->lambda_sq_pt() = &Global_Parameters::Lambda_sq;
  }

The fluid elements require pointers to the Reynolds and Womersley (product of Reynolds and Strouhal) numbers:

 
 
 
 // Complete build of fluid elements
 //---------------------------------
 
 // Set physical parameters in the fluid mesh
 unsigned nelem=fluid_mesh_pt()->nelement();
 for (unsigned e=0;e<nelem;e++)
  {
   // Upcast from GeneralisedElement to the present element
   FLUID_ELEMENT* el_pt = dynamic_cast<FLUID_ELEMENT*>
    (fluid_mesh_pt()->element_pt(e));
   
   //Set the Reynolds number
   el_pt->re_pt() = &Global_Parameters::Re;   
   
   //Set the Womersley number
   el_pt->re_st_pt() = &Global_Parameters::ReSt;
   
  }//end_of_loop

Setting up the fluid-structure interaction is done from "both" sides" of the fluid-solid interface: First we ensure that the no-slip condition is automatically applied to all fluid nodes that are located on the three faces of the flag (mesh boundaries 5, 6 and 7). This is done by passing the function pointer to the
FSI_functions::apply_no_slip_on_moving_wall() function to the relevant fluid nodes (recall that the auxiliary node update functions are automatically executed whenever the position of a node is updated by the algebraic node update). Since the no-slip condition (1) involves the Strouhal number (which, in the current problem, is not equal to the default value of FSI_functions::Strouhal_for_no_slip=1.0), we overwrite the default assignment with the actual Strouhal number in the problem.

 
 
 
 // Setup FSI
 //----------
 
 // Pass Strouhal number to the helper function that automatically applies
 // the no-slip condition
 FSI_functions::Strouhal_for_no_slip=Global_Parameters::St;
 
 // The velocity of the fluid nodes on the wall (fluid mesh boundary 5,6,7)
 // is set by the wall motion -- hence the no-slip condition must be
 // re-applied whenever a node update is performed for these nodes. 
 // Such tasks may be performed automatically by the auxiliary node update 
 // function specified by a function pointer:
 if (!Global_Parameters::Ignore_fluid_loading)
  {
   for(unsigned ibound=5;ibound<8;ibound++ )
    { 
     unsigned num_nod= Fluid_mesh_pt->nboundary_node(ibound);
     for (unsigned inod=0;inod<num_nod;inod++)
      {   
       Fluid_mesh_pt->boundary_node_pt(ibound, inod)->
        set_auxiliary_node_update_fct_pt(
         FSI_functions::apply_no_slip_on_moving_wall);
      }
    } // done automatic application of no-slip

Next, we set up the lookup schemes required by the FSISolidTractionElements to establish which fluid elements affect the traction onto the solid:

  
   // Work out which fluid dofs affect the residuals of the wall elements:
   // We pass the boundary between the fluid and solid meshes and 
   // pointers to the meshes. The interaction boundary are boundaries 5,6,7
   // of the 2D fluid mesh.
   FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
    (this,5,Fluid_mesh_pt,Traction_mesh_pt[0]);  
   
   FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
    (this,6,Fluid_mesh_pt,Traction_mesh_pt[2]);  
   
   FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
    (this,7,Fluid_mesh_pt,Traction_mesh_pt[1]); 
  } 

All interactions have now been specified and we conclude by assigning the equation numbers

 // Assign equation numbers
 cout << assign_eqn_numbers() << std::endl; 
 
 
}//end_of_constructor

Create traction elements

This is a helper function that attaches FSISolidTractionElement to the solid elements that are exposed to the fluid traction. We store the elements in three distinct sub-meshes – one for each face. (Yet another mesh, pointed to by Combined_traction_mesh_pt, is created for post-processing purposes.)

//============start_of_create_traction_elements==============================
/// Create FSI traction elements 
//=======================================================================
template<class FLUID_ELEMENT,class SOLID_ELEMENT >
void TurekProblem<FLUID_ELEMENT,SOLID_ELEMENT>::create_fsi_traction_elements()
{
 
 // Container to collect all nodes in the traction meshes
 std::set<SolidNode*> all_nodes;
 
 // Traction elements are located on boundaries 0-2:
 for (unsigned b=0;b<3;b++)
  {
   // How many bulk elements are adjacent to boundary b?
   unsigned n_element = solid_mesh_pt()->nboundary_element(b);
   
   // Loop over the bulk elements adjacent to boundary b?
   for(unsigned e=0;e<n_element;e++)
    {
     // Get pointer to the bulk element that is adjacent to boundary b
     SOLID_ELEMENT* bulk_elem_pt = dynamic_cast<SOLID_ELEMENT*>(
      solid_mesh_pt()->boundary_element_pt(b,e));
     
     //What is the index of the face of the element e along boundary b
     int face_index = solid_mesh_pt()->face_index_at_boundary(b,e);
          
     // Create new element and add to mesh
     Traction_mesh_pt[b]->add_element_pt(
      new FSISolidTractionElement<SOLID_ELEMENT,2>(bulk_elem_pt,face_index));
     
    } //end of loop over bulk elements adjacent to boundary b
 
   // Identify unique nodes
   unsigned nnod=solid_mesh_pt()->nboundary_node(b);
   for (unsigned j=0;j<nnod;j++)
    {
     all_nodes.insert(solid_mesh_pt()->boundary_node_pt(b,j));
    }
  }
 
 // Build combined mesh of fsi traction elements
 Combined_traction_mesh_pt=new SolidMesh(Traction_mesh_pt);
 
 // Stick nodes into combined traction mesh
 for (std::set<SolidNode*>::iterator it=all_nodes.begin();
      it!=all_nodes.end();it++)
  {
   Combined_traction_mesh_pt->add_node_pt(*it);
  }
 
} // end of create_traction_elements

Actions before Newton convergence check

The algebraic node-update procedure updates the positions in response to changes in the solid displacements but this is not done automatically when the Newton solver updates the solid mechanics degrees of freedom. We therefore force a node-update before the Newton convergence check.

//====start_of_actions_before_newton_convergence_check===================
/// Update the (dependent) fluid node positions following the
/// update of the solid variables
//=======================================================================
template <class FLUID_ELEMENT,class SOLID_ELEMENT> 
void TurekProblem<FLUID_ELEMENT,SOLID_ELEMENT>
::actions_before_newton_convergence_check ()
{
 fluid_mesh_pt()->node_update();
}

Actions before the timestep

Before each timestep we update the inflow profile for all fluid nodes on mesh boundary 3.

//===== start_of_actions_before_implicit_timestep=========================
/// Actions before implicit timestep: Update inflow profile
//========================================================================
template <class FLUID_ELEMENT,class SOLID_ELEMENT> 
void TurekProblem<FLUID_ELEMENT,SOLID_ELEMENT>::
actions_before_implicit_timestep()
{
 // Current time
 double t=time_pt()->time();
 
 // Amplitude of flow
 double ampl=Global_Parameters::flux(t);
 
 // Update parabolic flow along boundary 3
 unsigned ibound=3; 
 unsigned num_nod= Fluid_mesh_pt->nboundary_node(ibound);
 for (unsigned inod=0;inod<num_nod;inod++)
  {
   double ycoord = Fluid_mesh_pt->boundary_node_pt(ibound,inod)->x(1); 
   double uy = ampl*6.0*ycoord/Domain_height*(1.0-ycoord/Domain_height);
   Fluid_mesh_pt->boundary_node_pt(ibound,inod)->set_value(0,uy);
   Fluid_mesh_pt->boundary_node_pt(ibound,inod)->set_value(1,0.0);    
  }
 
} //end_of_actions_before_implicit_timestep

Actions after adapt

After each adaptation, we unpin and re-pin all redundant pressures degrees of freedom. This is necessary because their "redundant-ness" may have been altered by changes in the refinement pattern; see another tutorial for details. We ensure the automatic application of the no-slip condition on fluid nodes that are located on the faces of the flag, and re-setup the FSI lookup scheme that tells FSISolidTractionElements which fluid elements are located next to their Gauss points.

//=====================start_of_actions_after_adapt=======================
///  Actions after adapt: Re-setup FSI
//========================================================================
template<class FLUID_ELEMENT,class SOLID_ELEMENT >
void TurekProblem<FLUID_ELEMENT,SOLID_ELEMENT>::actions_after_adapt()
{
 // Unpin all pressure dofs
 RefineableNavierStokesEquations<2>::
  unpin_all_pressure_dofs(fluid_mesh_pt()->element_pt());
 
 // Pin redundant pressure dofs
 RefineableNavierStokesEquations<2>::
  pin_redundant_nodal_pressures(fluid_mesh_pt()->element_pt());
 
 // Unpin all solid pressure dofs
 PVDEquationsBase<2>::
  unpin_all_solid_pressure_dofs(solid_mesh_pt()->element_pt());
 
 // Pin the redundant solid pressures (if any)
 PVDEquationsBase<2>::pin_redundant_nodal_solid_pressures(
  solid_mesh_pt()->element_pt());
 
 
 // The velocity of the fluid nodes on the wall (fluid mesh boundary 5,6,7)
 // is set by the wall motion -- hence the no-slip condition must be
 // re-applied whenever a node update is performed for these nodes. 
 // Such tasks may be performed automatically by the auxiliary node update 
 // function specified by a function pointer:
 if (!Global_Parameters::Ignore_fluid_loading)
  {
   for(unsigned ibound=5;ibound<8;ibound++ )
    { 
     unsigned num_nod= Fluid_mesh_pt->nboundary_node(ibound);
     for (unsigned inod=0;inod<num_nod;inod++)
      {   
       Fluid_mesh_pt->boundary_node_pt(ibound, inod)->
        set_auxiliary_node_update_fct_pt(
         FSI_functions::apply_no_slip_on_moving_wall);
      }
    }
 
 
   // Re-setup the fluid load information for fsi solid traction elements
   FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
    (this,5,Fluid_mesh_pt,Traction_mesh_pt[0]); 
   
   FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
    (this,6,Fluid_mesh_pt,Traction_mesh_pt[2]); 
   
   FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
    (this,7,Fluid_mesh_pt,Traction_mesh_pt[1]); 
  }
 
 
}// end of actions_after_adapt

Post-processing

The function doc_solution(...) produces the output for the fluid, solid and traction meshes and writes selected data to the trace file.

//=====start_of_doc_solution========================================
/// Doc the solution
//==================================================================
template<class FLUID_ELEMENT,class SOLID_ELEMENT >
void TurekProblem<FLUID_ELEMENT,SOLID_ELEMENT>::doc_solution(
 DocInfo& doc_info, ofstream& trace_file)
{
 
//  FSI_functions::doc_fsi<AlgebraicNode>(Fluid_mesh_pt,
//                                        Combined_traction_mesh_pt,
//                                        doc_info);
 
//  pause("done");
 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned n_plot = 5; 
 
 // Output solid solution
 sprintf(filename,"%s/solid_soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 solid_mesh_pt()->output(some_file,n_plot);
 some_file.close();
 
 // Output fluid solution
 sprintf(filename,"%s/soln%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
 fluid_mesh_pt()->output(some_file,n_plot);
 some_file.close();
 
 
//Output the traction
 sprintf(filename,"%s/traction%i.dat",doc_info.directory().c_str(),
         doc_info.number());
 some_file.open(filename);
// Loop over the traction meshes
 for(unsigned i=0;i<3;i++)
  {
   // Loop over the element in traction_mesh_pt
   unsigned n_element = Traction_mesh_pt[i]->nelement();
   for(unsigned e=0;e<n_element;e++)
    {
     FSISolidTractionElement<SOLID_ELEMENT,2>* el_pt = 
      dynamic_cast<FSISolidTractionElement<SOLID_ELEMENT,2>* > (
       Traction_mesh_pt[i]->element_pt(e) );
     
     el_pt->output(some_file,5);
    }
  }
 some_file.close();  
 
 
 // Write trace (we're only using Taylor Hood elements so we know that
 // the pressure is the third value at the fluid control node...
 trace_file << time_pt()->time() << " " 
            << Solid_control_node_pt->x(0) << " " 
            << Solid_control_node_pt->x(1) << " " 
            << Fluid_control_node_pt->value(2) << " "
            << Global_Parameters::flux(time_pt()->time()) << " " 
            << std::endl;
 
 cout << "Doced solution for step " 
      << doc_info.number() 
      << std::endl << std::endl << std::endl;
 
}//end_of_doc_solution

Further comments and exercises

When completing the build of the FSISolidTractionElements (the elements that apply the fluid traction to the solid elements that are exposed to the fluid) we specified the number of the solid mesh boundary they are located on, using

elem_pt->set_boundary_number_in_bulk_mesh(bound);

This information is required when setting up the fluid-structure interaction because the MeshAsGeomObject representation of the mesh of FSISolidTractionElements is parametrised by the boundary coordinate in the solid mesh. Explore the details of the implementation by commenting out the relevant line of code and use the debugger to find out how and where the code fails. Note: Since this step is somewhat subtle and therefore easily forgotten, the FSISolidTractionElements issue an explicit warning if the bulk boundary number has not been set – but only if the the library is compiled in PARANOID mode.
When comparing our results against those in Turek & Hron's benchmark, we only focused on the period and amplitude of the fully-developed self-excited oscillations. The benchmark data also provides data on the time-dependent variations of the drag and lift coefficients. Design suitable FaceElements (to be attached to the faces of the Navier-Stokes elements that are adjacent to the flag or the cylinder) to compute these quantities. The NavierStokesSurfacePowerElements should provide a good basis for these.

Acknowledgements

This code was originally developed by Stefan Kollmannsberger and his students Iason Papaioannou and
Orkun Oezkan Doenmez. It was completed by Floraine Cordier.

Source files for this tutorial

The source files for this tutorial are located in the directory:

demo_drivers/interaction/turek_flag/
The driver code is:

demo_drivers/interaction/turek_flag/turek_flag.cc

PDF file

A pdf version of this document is available.