Parallel adaptive driven cavity problem with load balancing

In this tutorial we demonstrate how to perform load balancing to (re-)distribute elements between processors in parallel, distributed computations. Following a brief discussion of the underlying methodology, we illustrate the application in the adaptive driven cavity problem where the spatially non-uniform refinement of the mesh leads to a significant load imbalance.

Most of the driver code is identical to the codes discussed in the tutorials explaining the serial and distributed, parallel solution of the problem. Therefore we only discuss the changes required to perform load balancing on the problem.

Load balancing

The initial distribution of a problem via a call to

Problem::distribute(...)

attempts to distribute the elements in the Problem's mesh over the available processors such that (i) each processor stores approximately the same number of elements and (ii) the anticipated volume of inter-processor communication required to synchronise the solution across processor boundaries is minimised. Typically, this procedure works very well in the sense that the assembly times for the Jacobian matrix in a distributed computation scale extremely well with the number of processors.

A re-distribution of elements may be required because

  1. strongly non-uniform mesh adaptation may lead to a drastic increase in the number of elements on some processors;

  2. in multi-physics computations the cpu times required to compute the elements' contributions to the global Jacobian matrix may differ significantly between different element types. In such cases, the mere equidistribution of elements between processors will not achieve good parallel scaling;

  3. when restarting a computation on a larger number of processors, elements need to be re-distributed to populate the (otherwise empty) additional processors.

As with other methods within oomph-lib, load balancing is implemented such that only minimal user intervention is required. The function

Problem::load_balance()

may be called at any point following the distribution of the problem. The only change required to an existing driver code is the provision (via overloading of a broken virtual function in the Problem base class) of the function

Problem::build_mesh()

This function must

  1. Build the mesh (and in the case of multiple sub-meshes, build these and combine them to a global mesh using the Problem::build_global_mesh() function).

  2. Complete the build of the elements by setting pointers to physical parameters (such as Reynolds numbers) or functions (such as source function pointers), etc.

  3. Apply the boundary conditions.

  4. Perform any uniform mesh refinement that was applied before calling Problem::distribute().

Typically this requires no more than a straightforward cut-and-paste of code from the problem constructor into the Problem::build_mesh() function; see also the discussion What goes into the build_mesh() function? for more details.

The load balancing routines then perform the following steps:

  1. Take the current (distributed) global mesh, and calculate a new partition for each of the current elements, taking into account the cpu time that each element spent on the most recent computation of its contribution to the problem's Jacobian matrix.

  2. Build a new (global) mesh using the Problem::build_mesh() function.

  3. Distribute the new (global) mesh according to the new partitioning.

  4. Once distributed, refine the new (global) mesh on each processor to achieve the same refinement pattern as in the original problem.

  5. Copy the Data values from the old to the new (global) meshes.

We note that for "structured" meshes (i.e. meshes whose refinement pattern is represented by "tree forests") only complete trees can be moved between processors. If the mesh was refined uniformly after being distributed, a more fine-grained tree-forest (which may allow better load balancing) can be built by calling Problem::prune_halo_elements_and_nodes() as discussed in another tutorial.

An example: Revisiting the adaptive driven cavity problem

In this section we outline the required changes to the parallel version of the adaptive driven cavity problem so that the problem can use the load balancing method described above.

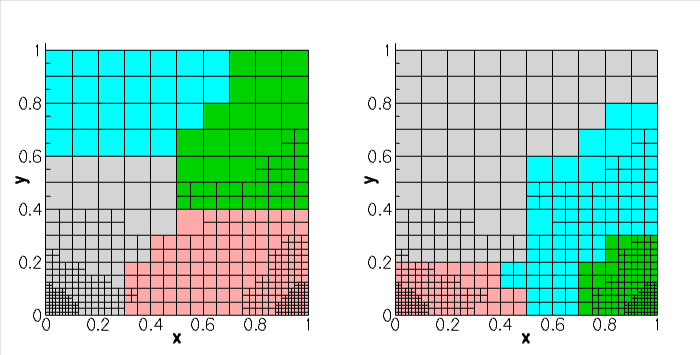
The figure below demonstrates the advantages of load balancing in that problem: The left hand panel shows the distribution of the mesh across four processors (indicated by the colours) after three spatially adaptive solves. Note how the singularities in the bottom corners result in a strongly non-uniform spatial refinement which leads to a significant load imbalance because the "pink" and "grey" processors contain far more elements than then "green" and "cyan" ones. The right hand panel shows the distribution of the mesh across four processors when load balancing is performed in between the second and third mesh adaptation.

Plot illustrating the distribution of the mesh for the adaptive driven cavity problem, both without (left image) and with (right image) the use of load balancing.

The build_mesh() function

As discussed above, the function Problem::build_mesh() is created most easily by moving the code that (i) creates the mesh, (ii) applies the relevant boundary conditions, and (iii) completes the build of all the elements in the problem from the problem constructor.

//==start_of_build_mesh===================================================
/// Build the mesh for RefineableDrivenCavity problem
///
//========================================================================
template<class ELEMENT>
void RefineableDrivenCavityProblem<ELEMENT>::build_mesh()
{
// Setup mesh
// # of elements in x-direction
unsigned n_x=10;
// # of elements in y-direction
unsigned n_y=10;
// Domain length in x-direction
double l_x=1.0;
// Domain length in y-direction
double l_y=1.0;
// Build and assign mesh
Problem::mesh_pt() =
new RefineableRectangularQuadMesh<ELEMENT>(n_x,n_y,l_x,l_y);
// Set error estimator
Z2ErrorEstimator* error_estimator_pt=new Z2ErrorEstimator;
dynamic_cast<RefineableRectangularQuadMesh<ELEMENT>*>(mesh_pt())->
spatial_error_estimator_pt()=error_estimator_pt;
// Fine tune error targets to get "interesting" refinement pattern
dynamic_cast<RefineableRectangularQuadMesh<ELEMENT>*>(mesh_pt())->
max_permitted_error()=1.0e-5;
dynamic_cast<RefineableRectangularQuadMesh<ELEMENT>*>(mesh_pt())->
min_permitted_error()=1.0e-6;
// Set the boundary conditions for this problem: All nodes are
// free by default -- just pin the ones that have Dirichlet conditions
// here: All boundaries are Dirichlet boundaries.
unsigned num_bound = mesh_pt()->nboundary();
for(unsigned ibound=0;ibound<num_bound;ibound++)
{
unsigned num_nod= mesh_pt()->nboundary_node(ibound);
for (unsigned inod=0;inod<num_nod;inod++)
{
// Loop over values (u and v velocities)
for (unsigned i=0;i<2;i++)
{
mesh_pt()->boundary_node_pt(ibound,inod)->pin(i);
}
}
} // end loop over boundaries
//Find number of elements in mesh
const unsigned n_element = mesh_pt()->nelement();
// Loop over the elements to set up element-specific
// things that cannot be handled by constructor: Pass pointer to Reynolds
// number
for(unsigned e=0;e<n_element;e++)
{
// Upcast from GeneralisedElement to the present element
ELEMENT* el_pt = dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(e));
//Set the Reynolds number
el_pt->re_pt() = &Global_Physical_Variables::Re;
} // end loop over elements
// Pin pressure at origin no matter which processor contains that node
pin_only_pressure_at_origin();
}// end_of_build_mesh

Changes to the problem constructor

The problem constructor becomes very short since the bulk of the code has been moved into the Problem::build_mesh() function.

//==start_of_constructor==================================================
/// Constructor for RefineableDrivenCavity problem
///
//========================================================================
template<class ELEMENT>
RefineableDrivenCavityProblem<ELEMENT>::RefineableDrivenCavityProblem()
{
// Set output directory
Doc_info.set_directory("RESLT_LOAD_BALANCE");
// Build the mesh
build_mesh();
// Setup equation numbering scheme
cout <<"Number of equations: " << assign_eqn_numbers() << std::endl;
} // end_of_constructor

Customising the load balancing

The driver code demonstrates some of the different options available for the Problem::load_balance(...) function.

  • Passing a boolean argument to Problem::load_balance(...) enables the output of extended statistics.

  • By default, the mesh partitioning for the initial problem distribution and any subsequent load balancing operations is determined by METIS. Unfortunately, METIS is not completely deterministic. This makes it difficult to compute reference data that can be used to assert the correct execution of the code during self-tests. When the driver code is run with the –validate command line flag, we therefore call the Problem::distribute(...) function with a pre-determined (and deterministic but non-optimal) distribution of the elements. The use of METIS during the load balancing operations can be bypassed by calling
    Problem::set_default_partition_in_load_balance()

Comments and Exercises

Comments

What goes into the build_mesh() function?

The main rule regarding what should (and should not) be moved from the problem constructor into the build_mesh() function is that following the return from the build_mesh() function, all meshes should be re-generated (and refined to the same degree as when Problem::distribute() was called), their constituent elements made fully functional, and all boundary conditions applied.

It is not necessary (and would, in fact, be undesirable) to re-create Timesteppers and/or GeomObjects that are used to define curvilinear mesh boundaries. We recommend generating such objects once (in the Problem constructor) and making them available to the build_mesh() function by storing pointers to them in the problem's private member data.

It is not necessary to re-generate the error estimator, though the pointer to it (and any non-default target errors) need to be passed to all (newly re-generated) adaptive meshes.

Updating pointers

Since load balancing re-generates the meshes – and thus their constituent elements and nodes – pointers to such objects must be re-assigned on return from Problem::load_balance(). In our experience such pointers tend to be used predominantly in

  • Post-processing functions (e.g. to document the solution at a fixed node)

  • Multi-physics/block preconditioners which tend to use pointers to meshes to classify the degrees of freedom.

Failure to re-assign any dangling pointers will cause segmentation faults – recompile oomph-lib with debugging enabled and use ddd to see where the code crashes.

Exercises

  1. Explore what happens if you "forget" to implement the Problem::build_mesh() function (e.g. by renaming it my_build_mesh(), say, so that it no longer overloads the function the Problem base class.

  2. The Problem::build_mesh() shown above (accidentally) illustrates a common problem with a mere cut-and-paste approach – it creates a memory leak! Where is it and how would you fix it?

  3. The demo_drivers directory contains a few additional driver codes that employ load balancing. These codes exist mainly for self-test purposes and do not have separate tutorials. It may be instructive to compare the different versions of these codes to further clarify the modifications required to enable load balancing. We suggest you compare

    Comparing the codes with sdiff is particularly instructive.

Source files for this tutorial

PDF file

A pdf version of this document is available.