Parallel solution of the adaptive driven cavity problem

This document concerns the parallel solution of the adaptive driven cavity problem. It is the first in a series of tutorials that discuss how to modify serial driver codes to distribute the Problem object across multiple processors.

Most of the driver code is identical to its serial counterpart and we only discuss the changes required to distribute the problem. Please refer to another tutorial for a more detailed discussion of the problem and its (serial) implementation.

---

The main function

As described in the parallel processing document all parallel driver codes must initialise and shutdown oomph-lib's MPI routines by calling MPI_Helpers::init(...) and MPI_Helpers::finalize(). The functions MPI_Helpers::init(...) and MPI_Helpers::finalize() call their MPI counterparts, MPI_Init(...) and MPI_Finalize(), which must not be called again.

In our demo driver codes, we surround all parallel sections of code with #ifdefs to ensure that the code remains functional if compiled without parallel support (in which case the macro OOMPH_HAS_MPI is undefined), for example.

//==start_of_main======================================================
/// Driver for RefineableDrivenCavity test problem 
//=====================================================================
int main(int argc, char **argv)
{
 
#ifdef OOMPH_HAS_MPI
 
 // Initialise MPI
 MPI_Helpers::init(argc,argv);
 
#endif

In order to distribute the problem over multiple processors a single call to the function Problem::distribute() is all that is required. Thus, a minimally-changed serial driver code would be

// Set output directory
DocInfo doc_info;
doc_info.set_directory("RESLT");
 
// Set max. number of black-box adaptation
unsigned max_adapt=3;
 
// Solve problem with Taylor Hood elements
//---------------------------------------
{
 //Build problem
 RefineableDrivenCavityProblem<RefineableQTaylorHoodElement<2> > problem;
 
 //Distribute the problem (only change from serial version)
 problem.distribute();         
 
 //Solve the problem with automatic adaptation
 problem.newton_solve(max_adapt);
 
 //Output solution
 problem.doc_solution(doc_info);
}

Finally, we must call MPI_finalize() before the end of the main function

// Finalise MPI
#ifdef OOMPH_HAS_MPI
 
 MPI_Helpers::finalize();
 
#endif
 
} // end_of_main

The actual driver code is slightly more complicated that the version shown above because it also acts as a self-test. The distribution of individual elements over the processors is determined by METIS and we have found that METIS occasionally gives slightly different results on different machines. To ensure reproducible results when acting as a self-test, the code (like all our parallel test codes) reads a predetermined element distribution from the disk; see below for more details.

---

Changes to the problem class

A particular feature of the driven cavity problem is that the flow is completely enclosed and that a single pressure degree of freedom must be prescribed. In the serial driver code, we arbitrarily pinned the first pressure degree of freedom in the "first" element in the mesh. Once the problem is distributed this element will only be available to particular processors and the pressure degree of freedom must be pinned on each one. Consequently we re-write the actions_after_adapt() function as follows:

 /// After adaptation: Unpin pressure and pin redundant pressure dofs.
 void actions_after_adapt()
  {
   // Unpin all pressure dofs
   RefineableNavierStokesEquations<2>::
    unpin_all_pressure_dofs(mesh_pt()->element_pt());
    
    // Pin redundant pressure dofs
   RefineableNavierStokesEquations<2>::
    pin_redundant_nodal_pressures(mesh_pt()->element_pt());
   
   // Now set the first pressure dof in the first element to 0.0
 
   // Loop over all elements
   const unsigned n_element=mesh_pt()->nelement();
   for (unsigned e=0;e<n_element;e++)
    {
     // If the lower left node of this element is (0,0), then fix the 
     // pressure dof in this element to zero
     if (mesh_pt()->finite_element_pt(e)->node_pt(0)->x(0)==0.0 && 
         mesh_pt()->finite_element_pt(e)->node_pt(0)->x(1)==0.0) // 2d problem
      {
       oomph_info << "I'm fixing the pressure " << std::endl;
       // Fix the pressure in element e at pdof=0 to 0.0
       unsigned pdof=0;
       fix_pressure(e,pdof,0.0);
      }
    }
 
  } // end_of_actions_after_adapt

This change ensures that every processor that holds the element containing the node at position (0,0) (i.e. the first element) fixes the pressure for that element. The floating-point comparison does not cause any problems in this case because the Node's position is explicitly set to "exactly" (0.0,0.0) in the Mesh constructor and never changes.

It is not necessary to change the corresponding statements in the problem constructor because the problem distribution occurs after the problem has been constructed. In fact, the problem constructor is unchanged from the serial version.

---

Changes to doc_solution

The doc_solution() routine requires a slight modification to ensure that the output from different processors can be distinguished; this is achieved by including the current processor number in the filename of the solution:

//==start_of_doc_solution=================================================
/// Doc the solution
//========================================================================
template<class ELEMENT>
void RefineableDrivenCavityProblem<ELEMENT>::doc_solution(DocInfo& doc_info)
{ 
 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned npts=5; 
 
 // Get current process rank
 int my_rank=this->communicator_pt()->my_rank();
 
 // Output solution 
 sprintf(filename,"%s/soln%i_on_proc%i.dat",doc_info.directory().c_str(),
         doc_info.number(),my_rank);
 some_file.open(filename);
 mesh_pt()->output(some_file,npts);
 some_file.close();
 
} // end_of_doc_solution

---

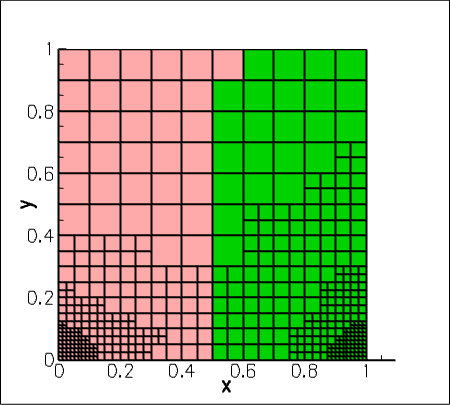
The figure below shows the mesh after the final solution of this problem, distributed across two processors, with the two colours indicating which processor the elements belong to.

Plot illustrating the distribution of the mesh for the adaptive driven cavity

---

Customising the distribution

The actual driver code demonstrates two of the different options available for the Problem::distribute() function, selected by the presence or absence of command line arguments.

Option I: Distributing a problem using METIS and documenting its distribution

If no command line arguments are specified we determine the problem distribution using METIS, and write the distribution to a file.

  //Are there command-line arguments?
  if (CommandLineArgs::Argc==1)
   {

The distribution is represented by a vector of unsigneds whose values indicate the processor on which the corresponding element is stored.

 
#ifdef OOMPH_HAS_MPI
 
    // Provide storage for each element's partition number
    const unsigned n_element=problem.mesh_pt()->nelement();
    Vector<unsigned> out_element_partition(n_element);

We distribute the problem with a call to Problem::distribute(...), using the boolean flag to request that the relevant statistics are displayed on screen. The distribution chosen for the elements is returned in the vector created earlier.

 
    // Distribute the problem
    bool report_stats=true;
    out_element_partition=problem.distribute(report_stats);

We document the distribution by writing the distribution vector to a file.

 
    // Write partition to disk
    std::ofstream output_file;
    char filename[100];
    sprintf(filename,"out_adaptive_cavity_1_partition.dat");
    output_file.open(filename);
    for (unsigned e=0;e<n_element;e++)
     {
      output_file << out_element_partition[e] << std::endl;
     }

Finally, we perform an optional self-test of the halo-haloed lookup schemes.

 
    // Check halo schemes (optional)
    problem.check_halo_schemes(doc_info);
 
#endif

---

Option II: Using a pre-determined distribution

If command line arguments are specified (typically when the code is run in validation mode) we read the distribution from disk, using a file that was written using the procedure shown above. (This is useful because in our experience METIS may produce slightly different distribution on different machines. This would cause the self-tests to fail even though the computed results would be correct).

We start by creating a DocInfo object that specifies the directory in which the problem distribution will be documented and by reading in the vector that represents the distribution

  // Validation run - read in partition from file
  else 
   {
 
#ifdef OOMPH_HAS_MPI
 
    // DocInfo object specifies directory in which we document
    // the distribution
    DocInfo mesh_doc_info;
    mesh_doc_info.set_directory("RESLT_TH_MESH");
 
    // Create storage for pre-determined partitioning
    const unsigned n_element=problem.mesh_pt()->nelement();
    Vector<unsigned> element_partition(n_element);
 
    // Read in partitioning from disk
    std::ifstream input_file;
    char filename[100];
    sprintf(filename,"adaptive_cavity_1_partition.dat");
    input_file.open(filename);
    std::string input_string;
    for (unsigned e=0;e<n_element;e++)
     {
      getline(input_file,input_string,'\n');
      element_partition[e]=atoi(input_string.c_str());
     }

We pass the distribution vector to Problem::distribute(...) and thus bypass the partitioning by METIS.

 
    // Now perform the distribution and document it
    bool report_stats=true;
    problem.distribute(element_partition,mesh_doc_info,report_stats);
 
#endif

We note that it is possible to document a mesh's distribution at any point, using the Mesh::doc_mesh_distribution(...) function, as indicated here

 
    // solve with adaptation
    problem.newton_solve(max_adapt);
 
    //Output solution
    problem.doc_solution(doc_info);
 
#ifdef OOMPH_HAS_MPI
 
    mesh_doc_info.number()=1;
    problem.mesh_pt()->doc_mesh_distribution(mesh_doc_info);
#endif
   }
 
 } // end of Taylor Hood elements

---

---

Source files for this tutorial

The driver code from which this example is taken also solves the same distributed problem using Crouzeix-Raviart elements. The fully modified parallel driver code can be found at

demo_drivers/mpi/distribution/adaptive_driven_cavity/adaptive_driven_cavity.cc

For further examples of using the distribute() function for both two-dimensional and three-dimensional single-domain problems, see the directory

demo_drivers/mpi/distribution/

---

---

PDF file

A pdf version of this document is available.