This tutorial demonstrates the use of unstructured meshes in 2D fluid-structure interaction problems with adaptivity. The formulation is extremely similar to that used in unstructured fsi without adaptivity, but the geometry of the problem is closely related to the flow in a channel with a leaflet using structured adaptivity.

The solid mechanics problem is exactly the same as that described in the unstructured solid mechanics with adaptivity tutorial. The fluid mechanics problem is new, but is a simple extension of the previous problems. The key realisation is that the unstructured refinement can take place independently for the fluid and solid domains provided that the common boundary between them has a common parametrisation. Moreover, the common boundary must have the same parametrisation in order for the fluid-structure interaction to be set up in the first place. Thus, setting up unstructured adaptivity for fsi problems is no more difficult than setting up the original unstructured problem using oomph-lib's inline unstructured mesh generation procedures.

The problem

The figure below shows a sketch of the problem. A 2D channel is partly obstructed by an elastic bar and has an imposed parabolic inlet velocity profile.

Sketch of the problem showing fluid and solid boundary

The non-dimension formulation is the same as described in the related non-adaptive problem. The fluid structure interaction parameter 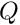is the ratio of viscous fluid stress to the reference stress (Young's modulus) of the solid.

Results

The figure below shows streamlines and pressure contours for the steady solution when 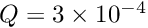$Q = 3\times 10^{-4}$ and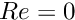

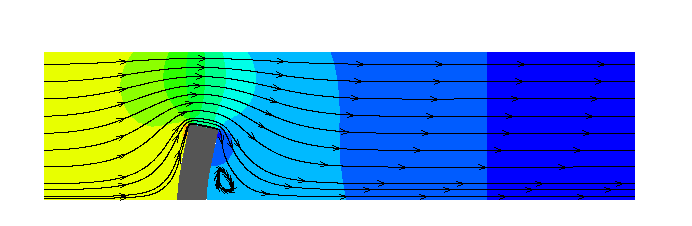
The flow field (streamlines and pressure contours) and the deformation of the elastic obstacle.

Overview of the implementation

The implementation is exactly the same as described in the non-adaptive unstructured mesh fluid-structure interaction problem. The only difference is that the meshes are constructed using oomph-lib's inline mesh generation procedures.

For simplicity the common boundaries between the fluid and solid mesh are assigned the same boundary ids, but this is not necessary. The boundary ids for each domain are shown in the sketch above.

Problem Parameters

The various problem parameters are defined in a global namespace. We define the Reynolds number, 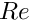, and the FSI interaction parameter .

//=======start_namespace==========================================
/// Global variables
//================================================================
namespace Global_Physical_Variables
{
 /// Reynolds number
 double Re = 0.0;
 
 /// FSI parameter
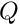 double Q = 0.0;

We specify the Poisson ratio of the solid and provide a pointer to the constitutive equation for the solid.

 
 /// Poisson's ratio
 double Nu=0.3;
 
 /// Pointer to constitutive law
 ConstitutiveLaw* Constitutive_law_pt=0;

The Poisson's ratio and pointer to a constitutive law for the mesh deformation is specified separately.

 
 /// Mesh poisson ratio
 double Mesh_Nu = 0.1;
 
 /// Pointer to constitutive law for the mesh
 ConstitutiveLaw* Mesh_constitutive_law_pt=0;
 
} //end namespace

The driver code

We set an output directory, trace file and instantiate the constitutive laws for the real and mesh solid mechanics computations with the appropriate Poisson ratios:

 DocInfo doc_info;
 
 // Output directory
 doc_info.set_directory("RESLT");
 
 //Create a trace file
 std::ofstream trace("RESLT/trace.dat");
 
 // Create generalised Hookean constitutive equations
 Global_Physical_Variables::Constitutive_law_pt = 
  new GeneralisedHookean(&Global_Physical_Variables::Nu);
 
 // Create generalised Hookean constitutive equations for the mesh as well
 Global_Physical_Variables::Mesh_constitutive_law_pt = 
  new GeneralisedHookean(&Global_Physical_Variables::Mesh_Nu);

We then create the Problem object and output the initial guess for the solution

 
 //Set up the problem
 UnstructuredFSIProblem<
 ProjectableTaylorHoodElement<
 PseudoSolidNodeUpdateElement<TTaylorHoodElement<2>, TPVDElement<2,3> > >, 
  ProjectablePVDElement<TPVDElement<2,3> > > problem;
 
//Output initial configuration
problem.doc_solution(doc_info);
doc_info.number()++;

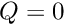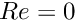Initially and , so the solid should remain undeformed and the fluid problem is linear. We expect to obtain the solution in one Newton iteration and so we perform one steady solve with the default mesh and output the result. We also output the strain energy of the solid and dissipation of the fluid as global measures of the solution that can be used for validation. (The unstructured meshes generated are not guaranteed to be exactly the same on different computers.)

 
// Solve the problem
problem.newton_solve();
 
//Output solution
problem.doc_solution(doc_info);
doc_info.number()++;
 
//Calculate the strain energy of the solid and dissipation in the
//fluid as global output measures of the solution for validation purposes
problem.output_strain_and_dissipation(trace);

Finally, we perform a parameter study by increasing 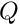, computing the result with one round of adaptivity and then writing the results to output files.

//Now Crank up interaction
for(unsigned i=0;i<n_step;i++)
 {
  Global_Physical_Variables::Q += 1.0e-4;
  problem.newton_solve(1);
 
  //Reset the lagrangian nodal coordinates in the fluid mesh
  //(Obviously we shouldn't do this in the solid mesh)
  problem.Fluid_mesh_pt->set_lagrangian_nodal_coordinates();
  //Output solution
  problem.doc_solution(doc_info);
  doc_info.number()++;
 
  //Calculate the strain energy of the solid and dissipation in the
  //fluid as global output measures of the solution for validation purposes
  problem.output_strain_and_dissipation(trace);
 }

The Problem class

The Problem class has a constructor, destructor and a post-processing member function. The class also includes the standard member functions actions_before_adapt() and actions_after_adapt(). There are private member functions that create and destroy the required FSISolidTractionElements that apply the load from the fluid on the solid and the ImposeDisplacementByLagrangeMultiplierElements that are used to (weakly) align the boundary of the fluid mesh with the solid domain. There are also private member functions to compute the fluid dissipation, solid strain energy and a public member function that outputs the computed strain and dissipation to a specified trace file.

The class provided storage for pointers to the Solid Mesh, the Fluid Mesh and vectors of pointers to meshes of FaceElements on the boundaries over which the interaction takes place. There is also storage for the GeomObject incarnations of fsi boundaries of the solid mesh and polygonal representations of the boundaries of the fluid and solid meshes.

The Problem constructor

We start by building the solid mesh, an associated error estimator and then writing the boundaries and mesh to output files. These steps are exactly the same as in the unstructured adaptive solid mechanics tutorial.

//===============start_constructor========================================
/// Constructor for unstructured solid problem
//========================================================================
template<class FLUID_ELEMENT, class SOLID_ELEMENT>
UnstructuredFSIProblem<FLUID_ELEMENT, SOLID_ELEMENT>::UnstructuredFSIProblem() 
{  
 
 //Some geometric parameters
 double x_inlet = 0.0;
 double channel_height = 1.0;
 double channel_length = 4.0;
 double x_leaflet = 1.0;
 double leaflet_width = 0.2;
 double leaflet_height = 0.5;
 
 // Solid Mesh
 //---------------
 
 // Build the boundary segments for outer boundary, consisting of
 //--------------------------------------------------------------
 // four separeate polyline segments
 //---------------------------------
 Vector<TriangleMeshCurveSection*> solid_boundary_segment_pt(4);
 
 // Initialize boundary segment
 Vector<Vector<double> > bound_seg(2);
 for(unsigned i=0;i<2;i++) {bound_seg[i].resize(2);}
 
 // First boundary segment
 bound_seg[0][0]=x_leaflet - 0.5*leaflet_width;
 bound_seg[0][1]=0.0;
 bound_seg[1][0]=x_leaflet - 0.5*leaflet_width;
 bound_seg[1][1]=leaflet_height;
 
 // Specify 1st boundary id
 unsigned bound_id = 0;
 
 // Build the 1st boundary segment
 solid_boundary_segment_pt[0] = new TriangleMeshPolyLine(bound_seg,bound_id);
 
 // Second boundary segment
 bound_seg[0][0]=x_leaflet - 0.5*leaflet_width;
 bound_seg[0][1]=leaflet_height;
 bound_seg[1][0]=x_leaflet + 0.5*leaflet_width;
 bound_seg[1][1]=leaflet_height;
 
 // Specify 2nd boundary id
 bound_id = 1;
 
 // Build the 2nd boundary segment
 solid_boundary_segment_pt[1] = new TriangleMeshPolyLine(bound_seg,bound_id);
 
 // Third boundary segment
 bound_seg[0][0]=x_leaflet + 0.5*leaflet_width;
 bound_seg[0][1]=leaflet_height;
 bound_seg[1][0]=x_leaflet + 0.5*leaflet_width;
 bound_seg[1][1]=0.0;
 
 // Specify 3rd boundary id
 bound_id = 2;
 
 // Build the 3rd boundary segment
 solid_boundary_segment_pt[2] = new TriangleMeshPolyLine(bound_seg,bound_id);
 
 // Fourth boundary segment
 bound_seg[0][0]=x_leaflet + 0.5*leaflet_width;
 bound_seg[0][1]=0.0;
 bound_seg[1][0]=x_leaflet - 0.5*leaflet_width;
 bound_seg[1][1]=0.0;
 
 // Specify 4th boundary id
 bound_id = 3;
 
 // Build the 4th boundary segment
 solid_boundary_segment_pt[3] = new TriangleMeshPolyLine(bound_seg,bound_id);
  
 // Create the triangle mesh polygon for outer boundary using boundary segment
 Solid_outer_boundary_polyline_pt = 
  new TriangleMeshPolygon(solid_boundary_segment_pt);
 
 // There are no holes
 //-------------------------------
 
 // Now build the mesh, based on the boundaries specified by
 //---------------------------------------------------------
 // polygons just created
 //----------------------
 double uniform_element_area= leaflet_width*leaflet_height/20.0;
 
 TriangleMeshClosedCurve* solid_closed_curve_pt=
  Solid_outer_boundary_polyline_pt;
 
 // Use the TriangleMeshParameters object for gathering all
 // the necessary arguments for the TriangleMesh object
 TriangleMeshParameters triangle_mesh_parameters_solid(
   solid_closed_curve_pt);
 
 // Define the maximum element area
 triangle_mesh_parameters_solid.element_area() =
   uniform_element_area;
 
 // Create the mesh
 Solid_mesh_pt =
   new RefineableSolidTriangleMesh<SOLID_ELEMENT>(
     triangle_mesh_parameters_solid);
 
 // Set error estimator for bulk mesh
 Z2ErrorEstimator* error_estimator_pt=new Z2ErrorEstimator;
 Solid_mesh_pt->spatial_error_estimator_pt()=error_estimator_pt;
 
 // Set targets for spatial adaptivity
 Solid_mesh_pt->max_permitted_error()=0.0001;
 Solid_mesh_pt->min_permitted_error()=0.001; 
 Solid_mesh_pt->max_element_size()=0.2;
 Solid_mesh_pt->min_element_size()=0.001; 
   
 // Output boundary and mesh
 this->Solid_mesh_pt->output_boundaries("solid_boundaries.dat");
 this->Solid_mesh_pt->output("solid_mesh.dat");

We next apply the boundary conditions to the solid mesh, by pinning the positions of the nodes on the lower boundary (boundary 3)

 
 // Pin both positions at lower boundary (boundary 3)
 unsigned ibound=3;
 unsigned num_nod= Solid_mesh_pt->nboundary_node(ibound);
 for (unsigned inod=0;inod<num_nod;inod++)
  {  
 
   // Get node
   SolidNode* nod_pt=Solid_mesh_pt->boundary_node_pt(ibound,inod);
   
   // Pin both directions
   for (unsigned i=0;i<2;i++)
    {
     nod_pt->pin_position(i);
    }
  } // end_solid_boundary_conditions

and complete the build of the solid elements by passing the pointer to the constitutive law to all elements in the solid mesh.

 
 // Complete the build of all elements so they are fully functional
 unsigned n_element = Solid_mesh_pt->nelement();
 for(unsigned i=0;i<n_element;i++)
  {
   //Cast to a solid element
   SOLID_ELEMENT *el_pt = 
    dynamic_cast<SOLID_ELEMENT*>(Solid_mesh_pt->element_pt(i));
   
   // Set the constitutive law
   el_pt->constitutive_law_pt() =
    Global_Physical_Variables::Constitutive_law_pt;
  }

The next task is to build the fluid mesh, which uses three of the boundary segments already constructed for the solid mesh for the common boundaries

 
 
 // Fluid Mesh
 //--------------
 
 // Build the boundary segments for outer boundary, consisting of
 //--------------------------------------------------------------
 // four separeate polyline segments
 //---------------------------------
 Vector<TriangleMeshCurveSection*> fluid_boundary_segment_pt(8);
 
 //The first three boundaries should be in common with the solid
 for(unsigned b=0;b<3;b++)
  {
   fluid_boundary_segment_pt[b] = solid_boundary_segment_pt[b];
  }

before constructing the remaining boundaries, building the mesh, an associated error estimator and writing the boundaries and mesh to output files.

 
 //Now fill in the rest 
 // Fourth boundary segment
 bound_seg[0][0]=x_leaflet + 0.5*leaflet_width;
 bound_seg[0][1]=0.0;
 bound_seg[1][0]=x_inlet + channel_length;
 bound_seg[1][1]=0.0;
 
 // Specify 4th boundary id
 bound_id = 3;
 
 // Build the 4th boundary segment
 fluid_boundary_segment_pt[3] = new TriangleMeshPolyLine(bound_seg,bound_id);
 
 // Fifth boundary segment
 bound_seg[0][0]=x_inlet + channel_length;
 bound_seg[0][1]=0.0;
 bound_seg[1][0]=x_inlet + channel_length;
 bound_seg[1][1]=channel_height;
 
 // Specify 5th boundary id
 bound_id = 4;
 
 // Build the 4th boundary segment
 fluid_boundary_segment_pt[4] = new TriangleMeshPolyLine(bound_seg,bound_id);
 
 // Sixth boundary segment
 bound_seg[0][0]=x_inlet + channel_length;
 bound_seg[0][1]=channel_height;
 bound_seg[1][0]=x_inlet;
 bound_seg[1][1]=channel_height;
 
 // Specify 6th boundary id
 bound_id = 5;
 
 // Build the 6th boundary segment
 fluid_boundary_segment_pt[5] = new TriangleMeshPolyLine(bound_seg,bound_id);
 
 // Seventh boundary segment
 bound_seg[0][0]=x_inlet;
 bound_seg[0][1]=channel_height;
 bound_seg[1][0]=x_inlet;
 bound_seg[1][1]=0.0;
 
 // Specify 7th boundary id
 bound_id = 6;
 
 // Build the 7th boundary segment
 fluid_boundary_segment_pt[6] = new TriangleMeshPolyLine(bound_seg,bound_id);
 
 // Eighth boundary segment
 bound_seg[0][0]=x_inlet;
 bound_seg[0][1]=0.0;
 bound_seg[1][0]=x_leaflet - 0.5*leaflet_width;
 bound_seg[1][1]=0.0;
 
 // Specify 8th boundary id
 bound_id = 7;
 
 // Build the 8th boundary segment
 fluid_boundary_segment_pt[7] = new TriangleMeshPolyLine(bound_seg,bound_id);
  
 // Create the triangle mesh polygon for outer boundary using boundary segment
 Fluid_outer_boundary_polyline_pt = 
  new TriangleMeshPolygon(fluid_boundary_segment_pt);
 
 // There are no holes
 //-------------------------------
 
 // Now build the mesh, based on the boundaries specified by
 //---------------------------------------------------------
 // polygons just created
 //----------------------
 uniform_element_area= channel_length*channel_height/40.0;;
 
 TriangleMeshClosedCurve* fluid_closed_curve_pt=
  Fluid_outer_boundary_polyline_pt;
 
 // Use the TriangleMeshParameters object for gathering all
 // the necessary arguments for the TriangleMesh object
 TriangleMeshParameters triangle_mesh_parameters_fluid(
   fluid_closed_curve_pt);
 
 // Define the maximum element area
 triangle_mesh_parameters_fluid.element_area() =
   uniform_element_area;
 
 // Create the mesh
 Fluid_mesh_pt =
   new RefineableSolidTriangleMesh<FLUID_ELEMENT>(
     triangle_mesh_parameters_fluid);
 
 // Set error estimator for bulk mesh
 Z2ErrorEstimator* fluid_error_estimator_pt=new Z2ErrorEstimator;
 Fluid_mesh_pt->spatial_error_estimator_pt()=fluid_error_estimator_pt;
 
 // Set targets for spatial adaptivity
 Fluid_mesh_pt->max_permitted_error()=0.0001;
 Fluid_mesh_pt->min_permitted_error()=0.001; 
 Fluid_mesh_pt->max_element_size()=0.2;
 Fluid_mesh_pt->min_element_size()=0.001; 
   
 // Output boundary and mesh
 this->Fluid_mesh_pt->output_boundaries("fluid_boundaries.dat");
 this->Fluid_mesh_pt->output("fluid_mesh.dat");

We then apply boundary conditions to the fluid mesh by pinning velocity everywhere apart from at the outflow (boundary 4) and pinning all nodal positions on all boundaries that are not in contact with the solid.

 
 // Set the boundary conditions for fluid problem: All nodes are
 // free by default 
 // --- just pin the ones that have Dirichlet conditions here. 
 
 //Pin velocity everywhere apart from parallel outflow (boundary 4)
 unsigned nbound=Fluid_mesh_pt->nboundary();
 for(unsigned ibound=0;ibound<nbound;ibound++)
  {
   unsigned num_nod=Fluid_mesh_pt->nboundary_node(ibound);
   for (unsigned inod=0;inod<num_nod;inod++)
    {
     // Pin velocity everywhere apart from outlet where we
     // have parallel outflow
     if (ibound!=4)
      {
       Fluid_mesh_pt->boundary_node_pt(ibound,inod)->pin(0); 
      }
     Fluid_mesh_pt->boundary_node_pt(ibound,inod)->pin(1); 
 
     // Pin pseudo-solid positions everywhere apart from boundaries 0, 1, 2 
     // the fsi boundaries
     if(ibound > 2)
      {
       for(unsigned i=0;i<2;i++)
        {
         // Pin the node
         SolidNode* nod_pt=Fluid_mesh_pt->boundary_node_pt(ibound,inod);
         nod_pt->pin_position(i);
        }
      }
    }
  } // end loop over boundaries

We next complete the build of the fluid elements by passing the Reynolds number and mesh constitutive law to all fluid elements

 
 
 // Complete the build of the fluid elements so they are fully functional
 n_element = Fluid_mesh_pt->nelement();
 for(unsigned e=0;e<n_element;e++)
  {
   // Upcast from GeneralisedElement to the present element
   FLUID_ELEMENT* el_pt = 
    dynamic_cast<FLUID_ELEMENT*>(Fluid_mesh_pt->element_pt(e));
   
   //Set the Reynolds number
   el_pt->re_pt() = &Global_Physical_Variables::Re;
   
   // Set the constitutive law for pseudo-elastic mesh deformation
   el_pt->constitutive_law_pt() =
    Global_Physical_Variables::Mesh_constitutive_law_pt;
   
  } // end loop over elements

and then set the Dirichlet boundary conditions for the fluid velocity on the inlet and channel walls.

 
 
 // Apply fluid boundary conditions: Poiseuille at inflow
 const unsigned n_boundary = Fluid_mesh_pt->nboundary();
 for (unsigned ibound=0;ibound<n_boundary;ibound++)
  {
   const unsigned num_nod= Fluid_mesh_pt->nboundary_node(ibound);
   for (unsigned inod=0;inod<num_nod;inod++)
    {
     // Parabolic inflow at the left boundary (boundary 6)
     if(ibound==6)
      {
       double y=Fluid_mesh_pt->boundary_node_pt(ibound,inod)->x(1);
       double veloc = y*(1.0-y);
       Fluid_mesh_pt->boundary_node_pt(ibound,inod)->set_value(0,veloc);
       Fluid_mesh_pt->boundary_node_pt(ibound,inod)->set_value(1,0.0);
      }
     // Zero flow elsewhere
     else 
      {
       Fluid_mesh_pt->boundary_node_pt(ibound,inod)->set_value(0,0.0);
       Fluid_mesh_pt->boundary_node_pt(ibound,inod)->set_value(1,0.0);
      }
    }
  } // end Poiseuille

We then build three meshes of traction elements corresponding to the solid boundaries 0,1 and 2 that bound the fluid

 
 
 // Make traction mesh 
 //(This must be done first because the resulting meshes are used
 // as the geometric objects that set the boundary locations of the fluid
 // mesh, as enforced by the Lagrange multipliers)
 Traction_mesh_pt.resize(3);
 for(unsigned m=0;m<3;m++) {Traction_mesh_pt[m] = new SolidMesh;}
 this->create_fsi_traction_elements();

and three analogous meshes of Lagrange multiplier elements.

 
 //Make the Lagrange multiplier mesh
 Lagrange_multiplier_mesh_pt.resize(3);
 Solid_fsi_boundary_pt.resize(3);
 for(unsigned m=0;m<3;m++) {Lagrange_multiplier_mesh_pt[m] = new SolidMesh;}
 this->create_lagrange_multiplier_elements();

The order matters because the Lagrange multiplier elements need pointers to the GeomObject incarnation of the FSITractionElements. Thus the traction elements must be created first.

We then combine all the sub meshes into a global mesh.

 
 // Add sub meshes
 add_sub_mesh(Fluid_mesh_pt);
 add_sub_mesh(Solid_mesh_pt);
 for(unsigned m=0;m<3;m++)
  {
   add_sub_mesh(Traction_mesh_pt[m]);
   add_sub_mesh(Lagrange_multiplier_mesh_pt[m]);
  }
 
 // Build global mesh
 build_global_mesh();

Finally, we setup the fluid-structure interaction for all three boundaries 0, 1 and 2 and then assign the equation numbers.

 
 // Setup FSI
 //----------
 // Work out which fluid dofs affect the residuals of the wall elements:
 // We pass the boundary between the fluid and solid meshes and 
 // pointers to the meshes. The interaction boundary are boundaries 0, 1 and 2
 // of the 2D fluid mesh.
 for(unsigned b=0;b<3;b++)
  {
   FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
    (this,b,Fluid_mesh_pt,Traction_mesh_pt[b]);
  }
   
 // Setup equation numbering scheme
 cout <<"Number of equations: " << assign_eqn_numbers() << std::endl; 
 
} //end constructor

Actions before adaptation

Before any adaptation takes place all surface meshes are deleted and the global mesh is rebuilt.

 /// Actions before adapt
 void actions_before_adapt()
  {
   //Delete the boundary meshes
   this->delete_lagrange_multiplier_elements();
   this->delete_fsi_traction_elements();
 
   //Rebuild the global mesh
   this->rebuild_global_mesh();
  }

Actions after adaptation

The adaptation is performed separately on the fluid and solid meshes and the order does not matter. In fact, the first mesh to be refined will be the first that is added as a sub mesh (in this case the fluid mesh). After adaptation of all meshes, we first reset the Lagrangian coordinates of the Fluid mesh to ensure that the mesh deformation is as robust as possible.

 
 
 /// Actions after adapt
 void actions_after_adapt()
  {
   //Ensure that the lagrangian coordinates of the mesh are set to be
   //the same as the eulerian
   Fluid_mesh_pt->set_lagrangian_nodal_coordinates();

Note that we must not reset the Lagrangian coordinates of the solid mesh because that would change the undeformed configuration of the solid.

We then reapply the solid boundary conditions and pass the constitutive law to the solid elements.

 
   //Apply boundary conditions again
   
   // Pin both positions at lower boundary (boundary 3)
   unsigned ibound=3;
   unsigned num_nod= Solid_mesh_pt->nboundary_node(ibound);
   for (unsigned inod=0;inod<num_nod;inod++)
    {  
     
     // Get node
     SolidNode* nod_pt=Solid_mesh_pt->boundary_node_pt(ibound,inod);
     
     // Pin both directions
     for (unsigned i=0;i<2;i++)
      {
       nod_pt->pin_position(i);
      }
    }
   
   // Complete the build of all elements so they are fully functional
   unsigned n_element = Solid_mesh_pt->nelement();
   for(unsigned i=0;i<n_element;i++)
    {
     //Cast to a solid element
     SOLID_ELEMENT *el_pt = 
      dynamic_cast<SOLID_ELEMENT*>(Solid_mesh_pt->element_pt(i));
     
     // Set the constitutive law
     el_pt->constitutive_law_pt() =
      Global_Physical_Variables::Constitutive_law_pt;
    } // end complete solid build

Next, the fluid boundary conditions are reapplied and the Reynolds number and mesh constitutive law are passed to all fluid elements.,

 
   
   // Set the boundary conditions for fluid problem: All nodes are
   // free by default 
   // --- just pin the ones that have Dirichlet conditions here. 
   
   //Pin velocity everywhere apart from parallel outflow (boundary 4)
   unsigned nbound=Fluid_mesh_pt->nboundary();
   for(unsigned ibound=0;ibound<nbound;ibound++)
    {
     unsigned num_nod=Fluid_mesh_pt->nboundary_node(ibound);
     for (unsigned inod=0;inod<num_nod;inod++)
      {
       // Pin velocity everywhere apart from outlet where we
       // have parallel outflow
       if (ibound!=4)
        {
         Fluid_mesh_pt->boundary_node_pt(ibound,inod)->pin(0); 
        }
       Fluid_mesh_pt->boundary_node_pt(ibound,inod)->pin(1); 
       
       // Pin pseudo-solid positions everywhere apart from boundaries 0, 1, 2 
       // the fsi boundaries
       if(ibound > 2)
        {
         for(unsigned i=0;i<2;i++)
          {
           // Pin the node
           SolidNode* nod_pt=Fluid_mesh_pt->boundary_node_pt(ibound,inod);
           nod_pt->pin_position(i);
          }
        }
      }
    } // end loop over boundaries
   
   
   // Complete the build of the fluid elements so they are fully functional
   n_element = Fluid_mesh_pt->nelement();
   for(unsigned e=0;e<n_element;e++)
    {
     // Upcast from GeneralisedElement to the present element
     FLUID_ELEMENT* el_pt = 
      dynamic_cast<FLUID_ELEMENT*>(Fluid_mesh_pt->element_pt(e));
     
     //Set the Reynolds number
     el_pt->re_pt() = &Global_Physical_Variables::Re;
     
     // Set the constitutive law for pseudo-elastic mesh deformation
     el_pt->constitutive_law_pt() =
      Global_Physical_Variables::Mesh_constitutive_law_pt;
     
    } // end loop over elements
   
   
   // Apply fluid boundary conditions: Poiseuille at inflow
   const unsigned n_boundary = Fluid_mesh_pt->nboundary();
   for (unsigned ibound=0;ibound<n_boundary;ibound++)
    {
     const unsigned num_nod= Fluid_mesh_pt->nboundary_node(ibound);
     for (unsigned inod=0;inod<num_nod;inod++)
      {
       // Parabolic inflow at the left boundary (boundary 6)
       if(ibound==6)
        {
         double y=Fluid_mesh_pt->boundary_node_pt(ibound,inod)->x(1);
         double veloc = y*(1.0-y);
         Fluid_mesh_pt->boundary_node_pt(ibound,inod)->set_value(0,veloc);
         Fluid_mesh_pt->boundary_node_pt(ibound,inod)->set_value(1,0.0);
        }
       // Zero flow elsewhere
       else 
        {
         Fluid_mesh_pt->boundary_node_pt(ibound,inod)->set_value(0,0.0);
         Fluid_mesh_pt->boundary_node_pt(ibound,inod)->set_value(1,0.0);
        }
      }
    } // end Poiseuille

We then create the traction and Lagrange multiplier elements and rebuild the global mesh. Again the traction elements must be created first because they are used by the Lagrange multiplier elements.

   
   //Recreate the boundary elements
   this->create_fsi_traction_elements();
   this->create_lagrange_multiplier_elements();
   
   //Rebuild the global mesh
   this->rebuild_global_mesh();

Finally, we setup the FSI on the three boundaries that are in common between the fluid and the solid.

 
 // Setup FSI (again)
 //------------------
 // Work out which fluid dofs affect the residuals of the wall elements:
 // We pass the boundary between the fluid and solid meshes and 
 // pointers to the meshes. The interaction boundary are boundaries 0, 1 and 2
 // of the 2D fluid mesh.
 for(unsigned b=0;b<3;b++)
  {
   FSI_functions::setup_fluid_load_info_for_solid_elements<FLUID_ELEMENT,2>
    (this,b,Fluid_mesh_pt,Traction_mesh_pt[b]);
  }

Creating and destroying the FSI traction and Lagrange multiplier elements

These functions are exactly the same (apart from the obvious changes in boundary id) as those described in the non-adaptive unstructured fsi tutorial. and are not repeated here.

Post-processing

The post-processing routine simply executes the output functions for the fluid and solid meshes and writes the results into separate files. Again this is exactly the same as in the non-adaptive case.

Comments and Exercises

The majority of comments in the non-adaptive unstructured FSI tutorial also apply here. As mentioned above, the reason why the methodology works so straightforwardly is because the parametrisation of common boundaries must be the same in the fluid and solid meshes. If not, setting up the fluid-structure interaction will not work even before any adaptation takes place. Thus, provided that your unstructured FSI problem has been correctly set up in the case without adaptivity, adding adaptivity is completely straightforward.

Exercises

Confirm that the order in which the sub-meshes are added does not affect the results.
Investigate the behaviour of the system under increasing Reynolds number.
Compare the results of the present (two-d elastic) problem to that of the (one-d) beam immersed within a channel. Do the results agree as the thickness of the two-d elastic bar decreases?
Modify your driver to perform unsteady runs and again compare your results to the one-dimensional beam code.

Source files for this tutorial

The source files for this tutorial are located in the directory:

demo_drivers/interaction/unstructured_adaptive_fsi
The driver code is:

demo_drivers/interaction/unstructured_adaptive_fsi/unstructured_adaptive_2d_fsi.cc

PDF file

A pdf version of this document is available.