Demo problem: Upgrading a GeomObject to a GeneralisedElement – how to parametrise unknown domain boundaries

In many previous examples we demonstrated how to use GeomObjects to parametrise curvilinear, moving domain boundaries. We used this functionality extensively to perform simulations of problems in moving domains. The techniques illustrated in these examples are adequate for problems in which the motion of the boundary is prescribed; see e.g. the
simulation of fluid flow in a 2D channel in which a part of one channel wall performs a prescribed oscillation.

Here we shall demonstrate how to use GeomObjects to parametrise curvilinear, moving domain boundaries in problem in which the position of the boundary is unknown and has to be determined as part of the overall solution. We will also address the following questions:

  • What is a GeomObject's geometric Data?
  • What is a GeneralisedElement's external and internal Data?

Part 1: A closer look at the GeomObject class: Geometric Data

In an earlier example, we introduced the GeomObject as a base class for all objects that provide an analytical parametrisation of a geometric object by specifying its Eulerian coordinates (i.e. the position vector to "material points" in the object, $ {\bf r}$) as a function of some intrinsic (Lagrangian) coordinates, $ {\bf \zeta} $, so that $ {\bf r} = {\bf r}({\bf \zeta})$. Every specific GeomObject must implement the pure virtual function

void GeomObject::position(const Vector<double>& zeta, Vector<double>& r);

where the number of Lagrangian and Eulerian coordinates involved in the parametrisation (i.e. the sizes of the vectors zeta and r) are stored as unsigned integers in the protected member data, GeomObject::NLagrangian and GeomObject::Ndim, respectively.

Most specific geometric objects store some additional parameters as private data members. For instance, a GeomObject that represents a 2D circle, parametrised by the 1D Lagrangian coordinate $ \zeta $ as

\[ {\bf r}(\zeta)= \left( \begin{array}{c} X_c + R \cos(\zeta) \\ Y_c + R \sin(\zeta) \end{array} \right) \]

may be implemented as follows:

//=====start_of_circle=====================================================
/// Simple circle in 2D space.
/// \f[ x = X_c + R \cos(\zeta) \f]
/// \f[ y = Y_c + R \sin(\zeta) \f]
//=========================================================================
class SimpleCircle : public GeomObject
{
public:
/// Constructor: Pass x and y-coords of centre and radius
SimpleCircle(const double& x_c, const double& y_c,
const double& r) : GeomObject(1,2), X_c(x_c), Y_c(y_c), R(r)
{}
/// Position Vector at Lagrangian coordinate zeta
void position(const Vector<double>& zeta, Vector<double>& r) const
{
// Position vector
r[0] = X_c+R*cos(zeta[0]);
r[1] = Y_c+R*sin(zeta[0]);
}
/// Position Vector at Lagrangian coordinate zeta at time level t
/// (t=0: present; t>0: previous level). Steady object, so we
/// simply forward the call to the steady version.
void position(const unsigned& t, const Vector<double>& zeta,
Vector<double>& r) const
{position(zeta,r);}
protected:
/// X-coordinate of centre
double X_c;
/// Y-coordinate of centre
double Y_c;
/// Radius
double R;
}; // end of SimpleCircle class

The shape and position of this GeomObject is defined by the parameters $ X_c, Y_c $ and $ R $ which are stored as double precision numbers in the object's private member data.

In many applications (e.g. in free-boundary problems) it is necessary to regard some (or all) of the parameters that specify the object's shape as (an) unknown(s) in the overall problem. Within oomph-lib all unknowns are values in Data objects. We refer to any Data objects whose values affect the shape of a GeomObject as the GeomObject's geometric Data. The GeomObject class defines interfaces for two functions that provide access to such Data. The function

virtual unsigned GeomObject::ngeom_data() const;

should return the number of geometric Data objects that affect a GeomObject's shape and position. The function

virtual Data* GeomObject::geom_data_pt(const unsigned& j);

should return a pointer to the GeomObject's j - th geometric Data object. Both functions are implemented as "broken" virtual functions in the GeomObject base class in order to facilitate the creation of new GeomObjects. The functions should be overloaded in GeomObjects that actually contain geometric Data. If this is not done, the broken versions in the base class issue a suitable explanation before throwing an error.

Here is a re-implementation of the above GeomObject in a form that allows the the parameters $ X_c, Y_c $ and $ R $ to be regarded as unknowns, by storing them as values in a suitable Data object:

//=========================================================================
/// GeneralCircle in 2D space.
/// \f[ x = X_c + R \cos(\zeta) \f]
/// \f[ y = Y_c + R \sin(\zeta) \f]
/// The three parameters \f$ X_c, Y_c \f$ and \f$ R \f$ are represented
/// by Data and can therefore be unknowns in the problem.
//=========================================================================
class GeneralCircle : public GeomObject
{

The object has two constructors which we will discuss separately. The arguments to the first constructor specify the x- and y-coordinates of the ring's centre ( $ X_c$ and $ Y_c$), and its radius, $ R $, as double-precision numbers. The constructor creates storage for these values in the Geom_data_pt vector which is stored in the object's protected member data. First, the Geom_data_pt vector (empty by default) is resized to provide storage for a (pointer to a) single Data item. Next we create a Data object that provides storage for three values and store the pointer to this Data object in the first (and only) component of the Geom_data_pt vector. Finally, we set the values to those specified by the arguments and pin them to reflect the fact that, by default, the values are constants rather than unknowns in the problem. [Note: Clearly, there is some ambiguity as to how to distribute the values of the geometric parameters among the geometric Data. Here we chose to store the three values in a single Data object, but we could also have stored each value in its own Data object.]

/// Constructor: Pass x and y-coords of centre and radius (all pinned)
GeneralCircle(const double& x_c, const double& y_c,
const double& r) : GeomObject(1,2)
{
// Create Data: We have one Data item with 3 values. The Data object
// stores the x position of the circle's centre as value 0,
// the y position of the circle's centre as value 1, and the
// circle's radius as value 2.
Geom_data_pt.resize(1);
Geom_data_pt[0] = new Data(3);
// Assign data: X_c -- the value is free by default: Need to pin it.
// Pin the data
Geom_data_pt[0]->pin(0);
// Give it a value:
Geom_data_pt[0]->set_value(0,x_c);
// Assign data: Y_c -- the value is free by default: Need to pin it.
// Pin the data
Geom_data_pt[0]->pin(1);
// Give it a value:
Geom_data_pt[0]->set_value(1,y_c);
// Assign data: R -- the value is free by default: Need to pin it.
// Pin the data
Geom_data_pt[0]->pin(2);
// Give it a value:
Geom_data_pt[0]->set_value(2,r);
// I've created the data, I need to clean up
Must_clean_up=true;
}

With this constructor, the geometric Data that controls the shape of the object is created internally – the "user" only specifies the values of the parameters. Their values are accessible via the access functions

/// Access function to x-coordinate of centre of circle
double& x_c(){return *Geom_data_pt[0]->value_pt(0);}
/// Access function to y-coordinate of centre of circle
double& y_c(){return *Geom_data_pt[0]->value_pt(1);}
/// Access function to radius of circle
double& R(){return *Geom_data_pt[0]->value_pt(2);}

but their internal representation as (pinned) values of a Data object remains hidden. Access to the geometric Data is, however, possible via the functions

/// How many items of Data does the shape of the object depend on?
unsigned ngeom_data() const {return Geom_data_pt.size();}
/// Return pointer to the j-th Data item that the object's
/// shape depends on
Data* geom_data_pt(const unsigned& j) {return Geom_data_pt[j];}

which overload the broken versions in the GeomObject base class. Both functions access the protected vector of pointers to the object's geometric Data:

protected:
/// Vector of pointers to Data items that affects the object's shape
Vector<Data*> Geom_data_pt;

The second constructor is appropriate for cases in which the Data object that specifies the object's shape has already been created elsewhere. In this case, we simply pass the pointer to the Data object to the constructor and store it in the first entry of the Geom_data_pt vector:

/// Alternative constructor: Pass x and y-coords of centre and radius
/// (all as part of Data)
/// \code
/// Geom_data_pt[0]->value(0) = X_c;
/// Geom_data_pt[0]->value(1) = Y_c;
/// Geom_data_pt[0]->value(2) = R;
/// \endcode
GeneralCircle(Data* geom_data_pt) : GeomObject(1,2)
{
#ifdef PARANOID
if (geom_data_pt->nvalue()!=3)
{
std::ostringstream error_stream;
error_stream << "Geometric Data must have 3 values, not "
<< geom_data_pt->nvalue() << std::endl;
throw OomphLibError(error_stream.str(),
OOMPH_CURRENT_FUNCTION,
OOMPH_EXCEPTION_LOCATION);
}
#endif
Geom_data_pt.resize(1);
Geom_data_pt[0]=geom_data_pt;
// Data has been created externally: Must not clean up
Must_clean_up=false;
} //end of alternative constructor

The boolean flag Must_clean_up is stored as private member data in the class. It is used in the destructor to decide if the geometric Data should be deleted. If the Data was created internally by the object (i.e. if the first constructor was used), the Data must also be deleted by the object; if the Data was created externally (i.e. if the second constructor was used), the Data must not be deleted as it may still be required in other parts of the code.

/// Destructor: Clean up if necessary
virtual ~GeneralCircle()
{
// Do I need to clean up?
if (Must_clean_up)
{
unsigned ngeom_data=Geom_data_pt.size();
for (unsigned i=0;i<ngeom_data;i++)
{
delete Geom_data_pt[i];
Geom_data_pt[i]=0;
}
}
} // end of destructor

The function GeomObject::position(...) simply extracts the relevant parameters ( $ X_c, Y_c, R $) from the Geom_data_pt vector and computes the position vector as a function of the 1D Lagrangian coordinate $ \zeta $:

/// Position Vector at Lagrangian coordinate zeta
void position(const Vector<double>& zeta, Vector<double>& r) const
{
// Extract data
double X_c= Geom_data_pt[0]->value(0);
double Y_c= Geom_data_pt[0]->value(1);
double R= Geom_data_pt[0]->value(2);
// Position vector
r[0] = X_c+R*cos(zeta[0]);
r[1] = Y_c+R*sin(zeta[0]);
} // end of position(...)

Part 2: Upgrading a GeomObject to a GeneralisedElement

We will now consider a (toy!) problem in which the ability to treat a parameter that specifies the shape and/or the position of a geometric object as an unknown (i.e. as a value in a Data object) is essential: A circular ring of radius $ R $ is mounted on a linearly elastic spring of stiffness $ k_{stiff} $. We wish to find the ring's equilibrium position when it is subjected to a vertical load, $ f_{load} $.

Sketch of the example problem.

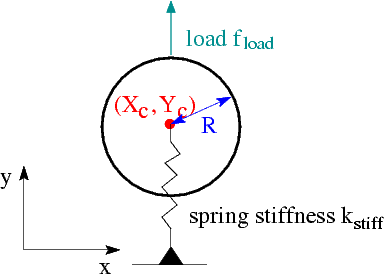
To solve this problem with oomph-lib [Yes, the solution is $ Y_c = f_{load}/k_{stiff}$ but let's pretend we don't know this...], we employ C++ inheritance to "upgrade" the GeneralCircle object, discussed above, to a GeneralisedElement in which the vertical position of the ring, $ Y_c $, is one of the unknowns whose value is determined by the equilibrium equation (in residual form),

\[ f_{load} - Y_c \ k_{stiff} = 0. \ \ \ \ \ \ \ \ \ \ \ (1) \]

In the present problem, the load on the ring is a control parameter, but in different applications it may be an unknown whose value has to be determined as part of the solution. (For instance, in fluid-structure interaction problems, the load on an elastic structure depends on the unknowns in the adjacent fluid elements.) Therefore, we also represent $ f_{load} $ by a Data object.

To solve the above problem with oomph-lib, the residual equation (1) must be implemented in the get_residuals(...) function of a suitable GeneralisedElement. Recall that the elemental residual vector computed by a GeneralisedElement can depend on two types of Data:

  • Internal Data stores values that are "internal" to the element, i.e. values that the element is "in charge of". Such Data is accessible via the pointer-based access function GeneralisedElement::internal_data_pt(...)
  • External Data stores values that are "external" to the element. The values stored in such Data affect the element's residual vector but its values are not determined by the element. Such Data is accessible via the pointer-based access function GeneralisedElement::external_data_pt(...)

In the present context, it is most natural to regard the GeneralCircle's geometric Data as internal to the element and the load Data as external.

Here is the class definition for the ElasticallySupportedRingElement which combines the GeneralisedElement and GeneralCircle classes by multiple inheritance. Its role as a GeomObject allows the object to be used in the parametrisation of domain boundaries; its role as a GeneralisedElement allows the value of $ Y_c $ to be determined as part of the solution.

//===========start_of_general_circle=========================================
/// GeneralCircle "upgraded" to a GeneralisedElement: Circular
/// ring whose position is given by
/// \f[ x = X_c + R \cos(\zeta) \f]
/// \f[ y = Y_c + R \sin(\zeta) \f]
/// The ring's vertical position \f$ Y_c \f$ is
/// determined by "pseudo elasticity":
/// \f[
/// 0 = f_{load} - Y_c \ k_{stiff}
/// \f]
/// This simulates the case where the centre of the ring is mounted on
/// an elastic spring of stiffness \f$ k_{stiff} \f$ and loaded by
/// the force \f$ f_{load}. \f$ The "load" is specified by the
/// Data object \c load_pt().
//=========================================================================
class ElasticallySupportedRingElement : public GeneralisedElement,
public GeneralCircle

The arguments to the constructor specify the initial geometric parameters, $ X_c, Y_c $ and $ R $. We pass them to the constructor of the GeneralCircle object and assign a default value for the spring stiffness $ k_{stiff}$ (stored as a private data member of the class; see below):

/// Constructor: Build ring from doubles that describe
/// the geometry: x and y positions of centre and the radius.
/// Initialise stiffness to 1.0. By default, no load is set.
ElasticallySupportedRingElement(const double& x_c, const double& y_c,
const double& r) :
GeneralCircle(x_c,y_c,r), K_stiff(1.0), Load_data_has_been_set(false)

Next, we add the GeneralCircle's geometric Data (created automatically by the constructor of the GeneralCircle object; see above) into the element's storage for its internal Data. This ensures that the geometric Data is included in the element's equation numbering procedures. Within the context of the GeneralCircle, all geometric parameters were regarded as constants and their values were pinned. Here, the vertical position [stored in the second entry in the geometric Data] is unknown, therefore we un-pin it.

{
// The geometric data is internal to the element -- we copy the pointers
// to the GeomObject's geometric data to the element's internal
// data to ensure that any unknown values of geometric data are
// given global equation numbers. The add_internal_data(...)
// function returns the index by which the added Data item
// is accessible from internal_data_pt(...).
Internal_geometric_data_index=add_internal_data(Geom_data_pt[0]);
// Geometric Data for the GeomObject has been set up (and pinned) in
// constructor for geometric object. Now free the y-position
// of the centre because we want to determine it as an unknown
internal_data_pt(Internal_geometric_data_index)->unpin(1);

Once Data has been added to a GeneralisedElement's internal Data, it is deleted by the destructor of the GeneralisedElement when the GeneralisedElement goes out of scope. The Data must therefore not be deleted again by the destructor of the GeneralCircle class, and we change the cleanup responsibilities accordingly:

// Change cleanup responsibilities: The GeomData will now be killed
// by the GeneralisedElement when it wipes its internal Data
Must_clean_up=false;
}

Since the GeneralisedElement's destructor will delete the internal Data, the destructor can remain empty:

/// Destructor:
virtual ~ElasticallySupportedRingElement()
{
// The GeomObject's GeomData is mirrored in the element's
// Internal Data and therefore gets wiped in the
// destructor of GeneralisedElement --> No need to kill it here
}

The Data whose one-and-only value represents the load must be set by the "user", using the function set_load_pt(...) As discussed above, we store the pointer to the load Data object in the GeneralisedElement's external Data and record its index within that storage scheme.

/// Set pointer to Data object that specifies the "load"
/// on the ElasticallySupportedRingElement
void set_load_pt(Data* load_pt)
{
#ifdef PARANOID
if (load_pt->nvalue()!=1)
{
std::ostringstream error_stream;
error_stream << "The data object that stores the load on the "
<< "ElasticallySupportedRingElement\n"
<< "should only contain a single data value\n"
<< "This one contains " << load_pt->nvalue() << std::endl;
throw OomphLibError(error_stream.str(),
OOMPH_CURRENT_FUNCTION,
OOMPH_EXCEPTION_LOCATION);
}
#endif
// Add load to the element's external data and store
// its index within that storage scheme: Following this assignment,
// the load Data is accessible from
// GeneralisedElement::external_data_pt(External_load_index)
External_load_index = add_external_data(load_pt);
// Load has now been set
Load_data_has_been_set=true;
} // end of set_load_pt(...)

[Note the sanity check which asserts that the load Data object only contains a single value; see Comments and Exercises for a further discussion of this aspect.]

The load() function provides access to the load specified by the load Data. It returns zero if no load was set – a sensible default.

/// "Load" acting on the ring
double load()
{
// Return the load if it has been set
if (Load_data_has_been_set)
{
return external_data_pt(External_load_index)->value(0);
}
// ...otherwise return zero load
else
{
return 0.0;
}
} // end of load()

Next, we provide an access functions to the spring stiffness parameter,

/// Access function for the spring stiffness
double& k_stiff() {return K_stiff;}

and functions that allow the vertical displacement of the ring to be pinned and un-pinned:

/// Pin the vertical displacement
void pin_yc()
{
// Vertical position of centre is stored as value 1 in the
// element's one and only internal Data object.
internal_data_pt(Internal_geometric_data_index)->pin(1);
}
/// Unpin the vertical displacement
void unpin_yc()
{
// Vertical position of centre is stored as value 1 in the
// element's one and only internal Data object.
internal_data_pt(Internal_geometric_data_index)->unpin(1);
} // end of unpin_yc()

Finally, we implement the pure virtual functions GeneralisedElement::get_jacobian(...) and GeneralisedElement::get_residuals(...) which are required to make the element functional. These functions must compute the element's contributions to the Problem's global residual vector and Jacobian matrix. As usual, we implement them as wrappers to a single function that computes the residual and (optionally) the Jacobian matrix:

/// Compute element residual vector (wrapper)
void get_residuals(Vector<double> &residuals)
{
//Initialise residuals to zero
residuals.initialise(0.0);
//Create a dummy matrix
DenseMatrix<double> dummy(1);
//Call the generic residuals function with flag set to 0
fill_in_generic_residual_contribution(residuals,dummy,0);
}
/// Compute element residual Vector and element Jacobian matrix (wrapper)
void get_jacobian(Vector<double> &residuals,
DenseMatrix<double> &jacobian)
{
//Initialise residuals to zero
residuals.initialise(0.0);
//Initialise the jacobian matrix to zero
jacobian.initialise(0.0);
//Call the generic routine with the flag set to 1
fill_in_generic_residual_contribution(residuals,jacobian,1);
} // end of get_jacobian(...)

The "real work" is done in the protected member function get_residuals_generic(...), where we distinguish two cases.

  1. The load is prescribed, i.e. the (single) value in the load Data object is pinned. In this case, the element's Data contains only one unknown – the vertical displacement $ Y_c $, stored as value 1 in the internal Data. The element's residual vector has a single entry, given by

    \[ {\tt r}_0 = f_{load} - Y_c \ k_{stiff} \]

    and the element's Jacobian matrix is a 1x1 matrix whose single entry is given by

    \[ {\tt J}_{00} = \frac{\partial {\tt r}_0}{\partial Y_c} = - k_{stiff} \]


  2. If the load is unknown (i.e. an unknown in the overall problem) the element's Data contains two unknowns. Recall that an element only makes a contribution to the residuals associated with unknowns that it is "in charge of" – the external Data is assumed to be "determined" by another element. Therefore, the elements residual vectors (i.e. its contribution to the Problem's global residual vector) is given by

    \[ \left( \begin{array}{c} {\tt r}_0 \\ {\tt r}_1 \end{array} \right) = \left( \begin{array}{c} f_{load} - Y_c \ k_{stiff}\\ 0 \end{array} \right). \]

    The element's 2x2 Jacobian matrix contains the derivatives of the residuals with respect to the element's unknowns, $ Y_c $ and $ f_{load}$,

    \[ \left( \begin{array}{cc} {\tt J}_{00} & {\tt J}_{01} \\ {\tt J}_{10} & {\tt J}_{11} \end{array} \right) = \left( \begin{array}{cc} \partial {\tt r}_0 / \partial Y_c& \partial {\tt r}_0 / \partial f_{load} \\ \partial {\tt r}_1 / \partial Y_c & \partial {\tt r}_1 / \partial f_{load} \end{array} \right) = \left( \begin{array}{cc} - k_{stiff} & 1 \\ 0 & 0 \end{array} \right) \]


Note that we have (correctly!) assumed that the (fully automatic) local equation numbering procedure, implemented in GeneralisedElement::assign_local_eqn_numbers(), regards the internal degree of freedom as local unknown "0" and the external one (if it exists) as unknown "1". However, to be on the safe side, we determine the local equation numbers via the access functions internal_local_eqn(i,j) and external_local_eqn(i,j), which return the local equation numbers of the j-th value, stored in the element's i-th internal (or external) Data object:

/// Compute element residual Vector (only if flag=0) and also
/// the element Jacobian matrix (if flag=1)
void fill_in_generic_residual_contribution(Vector<double> &residuals,
DenseMatrix<double> &jacobian,
unsigned flag)
{
//Find out how may dofs there are in the element
unsigned n_dof = ndof();
//If everything is pinned return straight away
if (n_dof==0) return;
// Pseudo-elastic force balance to determine the position of the
// ring's centre for a given load.
// What's the local equation number of the force balance equation
// [It's the equation that "determines" the value of the internal
// dof, y_c, which is stored as the second value of the one-and-only
// internal data object in this element]
int local_eqn_number_for_yc =
internal_local_eqn(Internal_geometric_data_index,1);
// Add residual to appropriate entry in the element's residual
// vector:
residuals[local_eqn_number_for_yc]=load()-K_stiff*y_c();
// Work out Jacobian:
if (flag)
{
// Derivative of residual w.r.t. the internal dof, i.e. the vertical
// position of the ring's centre: d residual[0]/d y_c
jacobian(local_eqn_number_for_yc,local_eqn_number_for_yc) = -K_stiff;
// Derivative with respect to external dof, i.e. the applied
// load: d residual[0]/d load -- but only if the load is an unknown
if (n_dof==2)
{
// What's the local equation number of the load parameter?
// It's stored as the 0th value in the the element's
// one-and-only external data item:
int local_eqn_number_for_load =
external_local_eqn(External_load_index,0);
#ifdef PARANOID
if (local_eqn_number_for_load<0)
{
throw OomphLibError(
"Load is pinned and yet n_dof=2?\n This is very fishy!\n",
OOMPH_CURRENT_FUNCTION,
OOMPH_EXCEPTION_LOCATION);
}
#endif
// Add entry into element Jacobian
jacobian(local_eqn_number_for_yc,local_eqn_number_for_load) = 1.0;
}
}
} // end of get_residuals_generic(...)

Part 3: The driver code

Finally, we provide an example that shows our ElasticallySupportedRingElement in action. The animation below shows the result of the computational simulation of the toy problem described at the beginning of the previous section: An elastically supported ring, subjected to a vertical load. The animation shows the position of the ring for various values of the load.

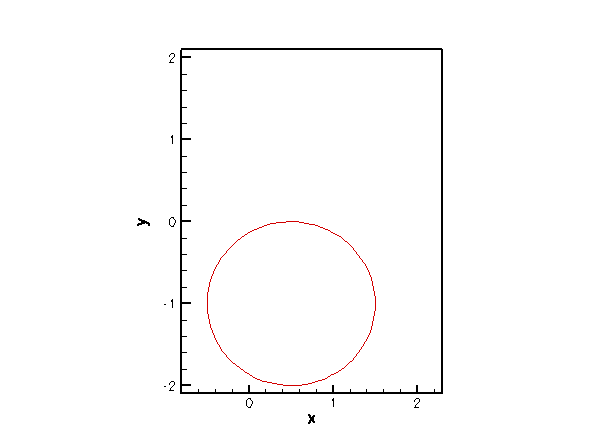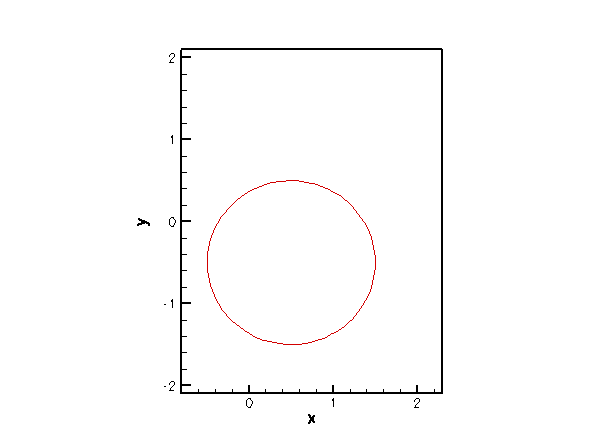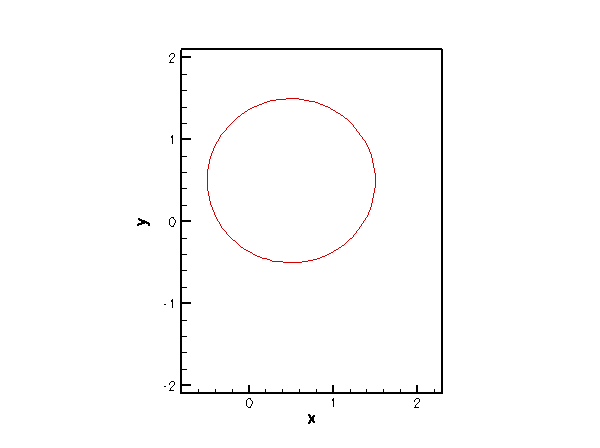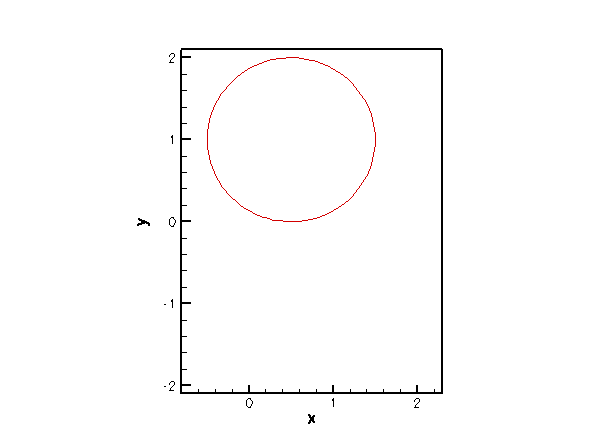
Vertical displacement of a Circle, mounted on an elastic support.

The driver code

The driver builds the Problem object and solves the problem for various load levels:

//===============start_of_driver==========================================
/// Driver
//========================================================================
int main()
{
// Set up the problem
GeomObjectAsGeneralisedElementProblem problem;
// Initial value for the load
problem.load()=-0.3;
// Loop for different loads
//-------------------------
// Number of steps
unsigned nstep=5;
// Increment in load
double dp=0.6/double(nstep-1);
for (unsigned istep=0;istep<nstep;istep++)
{
// Solve/doc
problem.newton_solve();
problem.doc_solution();
//Increment counter for solutions
problem.doc_info().number()++;
// Change load on ring
problem.load()+=dp;
}
} // end of driver
GeomObjectAsGeneralisedElementProblem
//////////////////////////////////////////////////////////////////// ////////////////////////////////...
Definition: geom_object_element.cc:53
GeomObjectAsGeneralisedElementProblem::doc_info
DocInfo & doc_info()
Access to DocInfo object.
Definition: geom_object_element.cc:76
GeomObjectAsGeneralisedElementProblem::load
double & load()
Return value of the "load" on the elastically supported ring.
Definition: geom_object_element.cc:70
main
int main()
///////////////////////////////////////////////////////////////////// ///////////////////////////////...
Definition: geom_object_element.cc:208

The problem class definition

Here is the problem class definition which requires little comment:

//======start_of_problem==============================================
/// Problem to demonstrate the use of a GeomObject as a
/// GeneralisedElement: A geometric object (a Circle) is "upgraded"
/// to a GeneralisedElement. The position of the Circle is
/// determined by a balance of forces, assuming that the
/// Circle is mounted on an elastic spring of specified
/// stiffness and loaded by a vertical "load".
//====================================================================
class GeomObjectAsGeneralisedElementProblem : public Problem
{
public:
/// Constructor
GeomObjectAsGeneralisedElementProblem();
/// Update the problem specs after solve (empty)
void actions_after_newton_solve(){}
/// Update the problem specs before solve (empty)
void actions_before_newton_solve() {}
/// Doc the solution
void doc_solution();
/// Return value of the "load" on the elastically supported ring
double& load()
{
return *Load_pt->value_pt(0);
}
/// Access to DocInfo object
DocInfo& doc_info() {return Doc_info;}
private:
/// Trace file
ofstream Trace_file;
/// Pointer to data item that stores the "load" on the ring
Data* Load_pt;
/// Doc info object
DocInfo Doc_info;
};
GeomObjectAsGeneralisedElementProblem::actions_before_newton_solve
void actions_before_newton_solve()
Update the problem specs before solve (empty)
Definition: geom_object_element.cc:64
GeomObjectAsGeneralisedElementProblem::Load_pt
Data * Load_pt
Pointer to data item that stores the "load" on the ring.
Definition: geom_object_element.cc:84
GeomObjectAsGeneralisedElementProblem::actions_after_newton_solve
void actions_after_newton_solve()
Update the problem specs after solve (empty)
Definition: geom_object_element.cc:61

The problem constructor

In the problem constructor, we create the (single) ElasticallySupportedRingElement and and assign a value to its "spring stiffness" parameter.

//=============================start_of_problem_constructor===============
/// Constructor
//========================================================================
GeomObjectAsGeneralisedElementProblem::GeomObjectAsGeneralisedElementProblem()
{
// Set coordinates and radius for the circle
double x_c=0.5;
double y_c=0.0;
double R=1.0;
// Build GeomObject that's been upgraded to a GeneralisedElement
// GeneralisedElement*
ElasticallySupportedRingElement* geom_object_element_pt =
new ElasticallySupportedRingElement(x_c,y_c,R);
// Set the stiffness of the elastic support
geom_object_element_pt->k_stiff()=0.3;

Next, we create the problem's mesh: We start by creating an (empty) Mesh object and then add the (pointer to the) newly created ElasticallySupportedRingElement (in its incarnation as a GeneralisedElement) to it:

// Build mesh
mesh_pt()=new Mesh;
// So far, the mesh is completely empty. Let's add the
// one (and only!) GeneralisedElement to it:
mesh_pt()->add_element_pt(geom_object_element_pt);

As discussed in the previous section, the load must be specified as a Data object that stores a single value. In our example, the load is prescribed (i.e. not an unknown in the problem) therefore the value must be pinned:

// Create the load (a Data object with a single value)
Load_pt=new Data(1);
// The load is prescribed so its one-and-only value is pinned
Load_pt->pin(0);
// Set the pointer to the Data object that specifies the
// load on the ring
geom_object_element_pt->set_load_pt(Load_pt);

Finally, we set up the equation numbering scheme, set the output directory and open a trace file in which we will document the load/displacement characteristics.

// Setup equation numbering scheme.
cout <<"Number of equations: " << assign_eqn_numbers() << std::endl;
// Set output directory
Doc_info.set_directory("RESLT");
// Open trace file
char filename[100];
sprintf(filename,"%s/trace.dat",Doc_info.directory().c_str());
Trace_file.open(filename);
Trace_file << "VARIABLES=\"load\",\"y<sub>circle</sub>\"" << std::endl;
} // end of constructor

The post-processing function

The post-processing routine is straightforward and is listed only to highlight the need to cast the pointer to the GeneralisedElement (as returned by Mesh::element_pt(...)) to the specific element used here – obviously, a GeneralisedElement does not have member functions that return the load on the ring or its vertical displacement.

//===========================start_of_doc_solution========================
/// Doc the solution in tecplot format.
//========================================================================
void GeomObjectAsGeneralisedElementProblem::doc_solution()
{
ofstream some_file;
char filename[100];
// Number of plot points
unsigned npts=100;
// Lagrangian coordinate and position vector (both as vectors)
Vector<double> zeta(1);
Vector<double> r(2);
// Output solution
sprintf(filename,"%s/soln%i.dat",Doc_info.directory().c_str(),
Doc_info.number());
some_file.open(filename);
for (unsigned i=0;i<npts;i++)
{
zeta[0]=2.0*MathematicalConstants::Pi*double(i)/double(npts-1);
static_cast<ElasticallySupportedRingElement*>(mesh_pt()->element_pt(0))->
position(zeta,r);
some_file << r[0] << " " << r[1] << std::endl;
}
some_file.close();
// Write "load" and vertical position of the ring's centre
Trace_file
<< static_cast<ElasticallySupportedRingElement*>(
mesh_pt()->element_pt(0))->load()
<< " "
<< static_cast<ElasticallySupportedRingElement*>(
mesh_pt()->element_pt(0))->y_c()
<< " "
<< std::endl;
} // end of doc_solution

Comments and Exercises

Exercises

  1. In the current implementation of the ElasticallySupportedRingElement, the load Data must only store a single value: Generalise this to the case where the Data object can contain an arbitrary number of values. You could add an additional argument to the set_load_pt(...) function to specify which value in the Data object represents the load. Think carefully in which other parts of the code this index will be required.

Source files for this tutorial

PDF file

A pdf version of this document is available.