In this problem we will discuss the 2D advection-diffusion problem with Neumann (flux) boundary conditions, using oomph-lib's mesh adaptation routines.
|
As always, we validate the code by choosing the boundary data and the source functions such that
![]()
is the exact solution of the problem. The plot below shows the numerical solution for ![]() , a Peclet number of
, a Peclet number of ![]() , and four different values of the "steepness parameter",
, and four different values of the "steepness parameter", ![]() and
and ![]() .
.
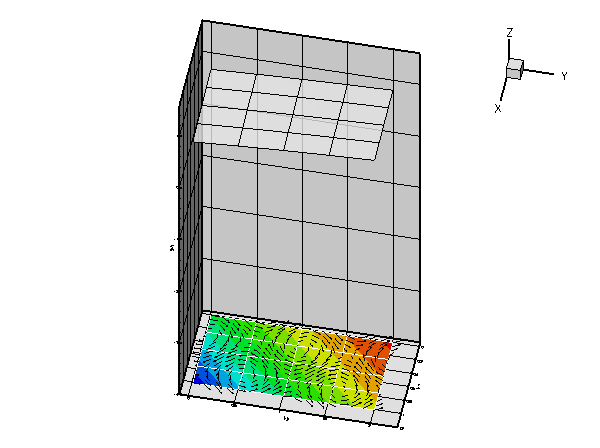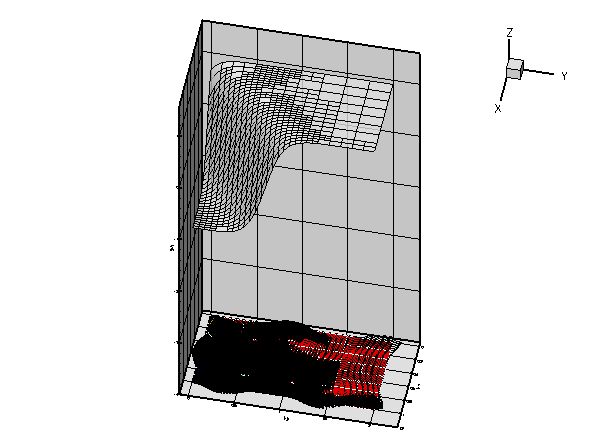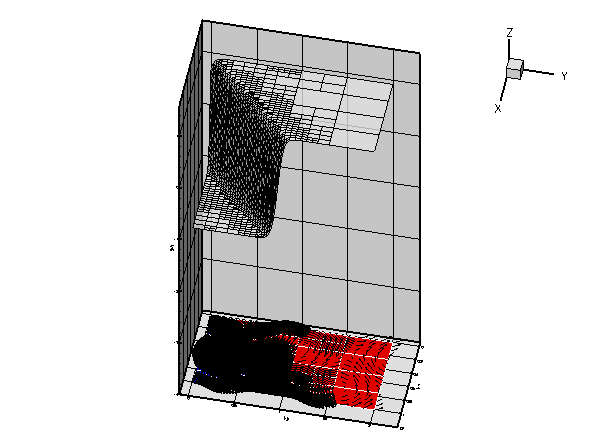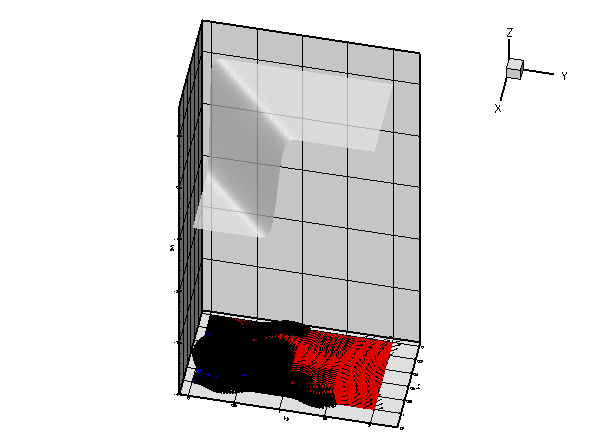
As in the example with Dirichlet boundary conditions, the unforced case is a lot more interesting. The plot below shows the result for a zero source function ![]() , Dirichlet boundary conditions determined from the "exact solution" of the forced problem for
, Dirichlet boundary conditions determined from the "exact solution" of the forced problem for ![]() , and a prescribed flux of
, and a prescribed flux of ![]() on
on ![]() .
.
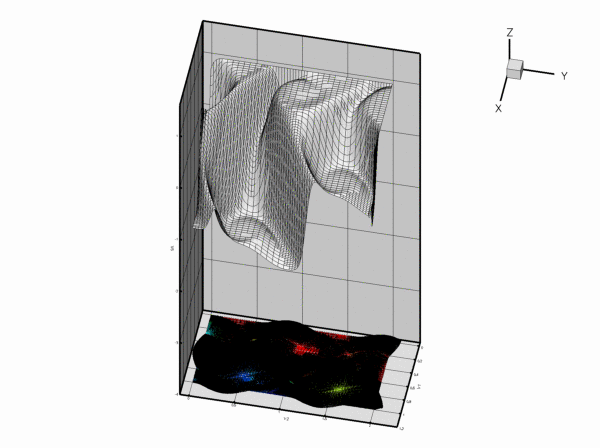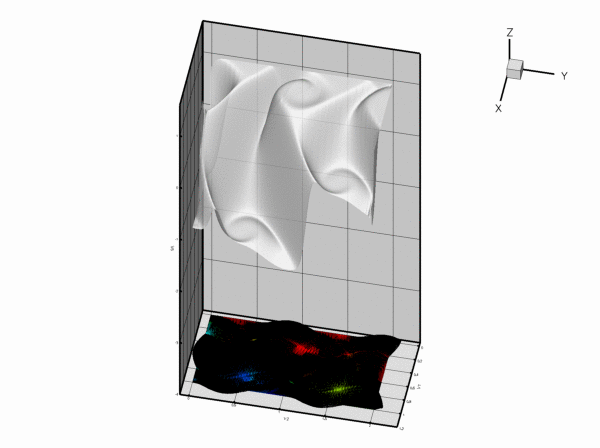
Along ![]() , the value of
, the value of ![]() is enforced by the Dirichlet boundary condition (2) and, as in the previous example, the "wind" either sweeps this value into the interior of the domain or creates a sharp boundary layer within which the solution that is "swept" along from the interior adjusts itself to the prescribed boundary value. Along
is enforced by the Dirichlet boundary condition (2) and, as in the previous example, the "wind" either sweeps this value into the interior of the domain or creates a sharp boundary layer within which the solution that is "swept" along from the interior adjusts itself to the prescribed boundary value. Along ![]() , the flux boundary condition (3) imposes the normal derivative of the solution. This boundary condition is much "softer" than the Dirichlet condition and does not create boundary layers that are as sharp as the ones that develop on
, the flux boundary condition (3) imposes the normal derivative of the solution. This boundary condition is much "softer" than the Dirichlet condition and does not create boundary layers that are as sharp as the ones that develop on ![]() .
.
The driver code
The driver code for this problem is so similar to the corresponding Poisson problem that we do not list it here. The modifications are the same as those discussed in the advection diffusion problem with Dirichlet boundary conditions: We have to specify the wind function and the Peclet number.
Source files for this tutorial
- The source files for this tutorial are located in the directory:
demo_drivers/advection_diffusion/two_d_adv_diff_flux_bc/ - The driver code is:
demo_drivers/advection_diffusion/two_d_adv_diff_flux_bc/two_d_adv_diff_flux_bc.cc
PDF file
A pdf version of this document is available. \