Public Member Functions | Protected Member Functions | List of all members
oomph::ConstitutiveLaw Class Referenceabstract

///////////////////////////////////////////////////////////////// ///////////////////////////////////////////////////////////////// More...

#include <constitutive_laws.h>

+ Inheritance diagram for oomph::ConstitutiveLaw:

Public Member Functions

 ConstitutiveLaw ()
 Empty constructor. More...
 
virtual ~ConstitutiveLaw ()
 Empty virtual destructor. More...
 
virtual void calculate_second_piola_kirchhoff_stress (const DenseMatrix< double > &g, const DenseMatrix< double > &G, DenseMatrix< double > &sigma)=0
 Calculate the contravariant 2nd Piola Kirchhoff stress tensor. Arguments are the covariant undeformed and deformed metric tensor and the matrix in which to return the stress tensor. More...
 
virtual void calculate_d_second_piola_kirchhoff_stress_dG (const DenseMatrix< double > &g, const DenseMatrix< double > &G, const DenseMatrix< double > &sigma, RankFourTensor< double > &d_sigma_dG, const bool &symmetrize_tensor=true)
 Calculate the derivatives of the contravariant 2nd Piola Kirchhoff stress tensor with respect to the deformed metric tensor. Arguments are the covariant undeformed and deformed metric tensor, the current value of the stress tensor and the rank four tensor in which to return the derivatives of the stress tensor The default implementation uses finite differences, but can be overloaded for constitutive laws in which an analytic formulation is possible. If the boolean flag symmetrize_tensor is false, only the "upper triangular" entries of the tensor will be filled in. This is a useful efficiency when using the derivatives in Jacobian calculations. More...
 
virtual void calculate_second_piola_kirchhoff_stress (const DenseMatrix< double > &g, const DenseMatrix< double > &G, DenseMatrix< double > &sigma_dev, DenseMatrix< double > &G_contra, double &Gdet)
 Calculate the deviatoric part $ \overline{ \sigma^{ij}}$ of the contravariant 2nd Piola Kirchhoff stress tensor $ \sigma^{ij}$. Also return the contravariant deformed metric tensor and the determinant of the deformed metric tensor. This form is appropriate for truly-incompressible materials for which $ \sigma^{ij} = - p G^{ij} +\overline{ \sigma^{ij}} $ where the "pressure" $ p $ is determined by $ \det G_{ij} - \det g_{ij} = 0 $. More...
 
virtual void calculate_d_second_piola_kirchhoff_stress_dG (const DenseMatrix< double > &g, const DenseMatrix< double > &G, const DenseMatrix< double > &sigma, const double &detG, const double &interpolated_solid_p, RankFourTensor< double > &d_sigma_dG, DenseMatrix< double > &d_detG_dG, const bool &symmetrize_tensor=true)
 Calculate the derivatives of the contravariant 2nd Piola Kirchhoff stress tensor $ \sigma^{ij}$. with respect to the deformed metric tensor. Also return the derivatives of the determinant of the deformed metric tensor with respect to the deformed metric tensor. This form is appropriate for truly-incompressible materials. The default implementation uses finite differences for the derivatives that depend on the constitutive law, but not for the derivatives of the determinant, which are generic. / If the boolean flag symmetrize_tensor is false, only the "upper triangular" entries of the tensor will be filled in. This is a useful efficiency when using the derivatives in Jacobian calculations. More...
 
virtual void calculate_second_piola_kirchhoff_stress (const DenseMatrix< double > &g, const DenseMatrix< double > &G, DenseMatrix< double > &sigma_dev, DenseMatrix< double > &Gcontra, double &gen_dil, double &inv_kappa)
 Calculate the deviatoric part of the contravariant 2nd Piola Kirchoff stress tensor. Also return the contravariant deformed metric tensor, the generalised dilatation, $ d, $ and the inverse of the bulk modulus $ \kappa$. This form is appropriate for near-incompressible materials for which $ \sigma^{ij} = -p G^{ij} + \overline{ \sigma^{ij}} $ where the "pressure" $ p $ is determined from $ p / \kappa - d =0 $. More...
 
virtual void calculate_d_second_piola_kirchhoff_stress_dG (const DenseMatrix< double > &g, const DenseMatrix< double > &G, const DenseMatrix< double > &sigma, const double &gen_dil, const double &inv_kappa, const double &interpolated_solid_p, RankFourTensor< double > &d_sigma_dG, DenseMatrix< double > &d_gen_dil_dG, const bool &symmetrize_tensor=true)
 Calculate the derivatives of the contravariant 2nd Piola Kirchoff stress tensor with respect to the deformed metric tensor. Also return the derivatives of the generalised dilatation, $ d, $ with respect to the deformed metric tensor. This form is appropriate for near-incompressible materials. The default implementation uses finite differences. If the boolean flag symmetrize_tensor is false, only the "upper triangular" entries of the tensor will be filled in. This is a useful efficiency when using the derivatives in Jacobian calculations. More...
 
virtual bool requires_incompressibility_constraint ()=0
 Pure virtual function in which the user must declare if the constitutive equation requires an incompressible formulation in which the volume constraint is enforced explicitly. Used as a sanity check in PARANOID mode. More...
 

Protected Member Functions

bool is_matrix_square (const DenseMatrix< double > &M)
 Test whether a matrix is square. More...
 
bool are_matrices_of_equal_dimensions (const DenseMatrix< double > &M1, const DenseMatrix< double > &M2)
 Test whether two matrices are of equal dimensions. More...
 
void error_checking_in_input (const DenseMatrix< double > &g, const DenseMatrix< double > &G, DenseMatrix< double > &sigma)
 Check for errors in the input, i.e. check that the dimensions of the arrays are all consistent. More...
 
double calculate_contravariant (const DenseMatrix< double > &Gcov, DenseMatrix< double > &Gcontra)
 Calculate a contravariant tensor from a covariant tensor, and return the determinant of the covariant tensor. More...
 
void calculate_d_contravariant_dG (const DenseMatrix< double > &Gcov, RankFourTensor< double > &dGcontra_dG, DenseMatrix< double > &d_detG_dG)
 Calculate the derivatives of the contravariant tensor and the derivatives of the determinant of the covariant tensor with respect to the components of the covariant tensor. More...
 

Detailed Description

///////////////////////////////////////////////////////////////// /////////////////////////////////////////////////////////////////

A class for constitutive laws for elements that solve the equations of solid mechanics based upon the principle of virtual displacements. In that formulation, the information required from a constitutive law is the (2nd Piola-Kirchhoff) stress tensor $ \sigma^{ij} $ as a function of the (Green) strain $ \gamma^{ij} $:

\[ \sigma^{ij} = \sigma^{ij}(\gamma_{ij}). \]

The Green strain is defined as

\[ \gamma_{ij} = \frac{1}{2} (G_{ij} - g_{ij}), \ \ \ \ \ \ \ \ \ \ \ (1) \]

where $G_{ij} $ and $ g_{ij}$ are the metric tensors in the deformed and undeformed (stress-free) configurations, respectively. A specific ConstitutiveLaw needs to be implement the pure virtual function

ConstitutiveLaw::calculate_second_piola_kirchhoff_stress(...)
oomph::ConstitutiveLaw::calculate_second_piola_kirchhoff_stress
virtual void calculate_second_piola_kirchhoff_stress(const DenseMatrix< double > &g, const DenseMatrix< double > &G, DenseMatrix< double > &sigma)=0
Calculate the contravariant 2nd Piola Kirchhoff stress tensor. Arguments are the covariant undeformed...

Equation (1) shows that the strain may be calculated from the undeformed and deformed metric tensors. Frequently, these tensors are also required in the constitutive law itself. To avoid unnecessary re-computation of these quantities, we pass the deformed and undeformed metric tensor to calculate_second_piola_kirchhoff_stress(...) rather than the strain tensor itself.

The functional form of the constitutive equation is different for compressible/incompressible/near-incompressible behaviour and we provide interfaces that are appropriate for all of these cases.

  1. Compressible Behaviour:
    If the material is compressible, the stress can be computed from the deformed and undeformed metric tensors,

    \[ \sigma^{ij} = \sigma^{ij}(\gamma_{ij}) = \sigma^{ij}\bigg( \frac{1}{2} (G_{ij} - g_{ij})\bigg), \]

    using the interface

    // 2nd Piola Kirchhoff stress tensor
    DenseMatrix<double> sigma(DIM,DIM);
    // Metric tensor in the undeformed (stress-free) configuration
    DenseMatrix<double> g(DIM,DIM);
    // Metric tensor in the deformed configuration
    DenseMatrix<double> G(DIM,DIM);
    // Compute stress from the two metric tensors:
    calculate_second_piola_kirchhoff_stress(g,G,sigma);




  2. Incompressible Behaviour:
    If the material is incompressible, its deformation is constrained by the condition that

    \[ \det G_{ij} - \det g_{ij}= 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \]

    which ensures that the volume of infinitesimal material elements remains constant during the deformation. This condition is typically enforced by a Lagrange multiplier which plays the role of a pressure. In such cases, the stress tensor has form

    \[ \sigma^{ij} = -p G^{ij} + \overline{\sigma}^{ij}\big(\gamma_{kl}\big), \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \]

    where only the deviatoric part of the stress tensor, 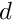$ \overline{\sigma}^{ij}, $ depends directly on the strain. The pressure 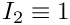$ p $ needs to be determined independently from (2). Given the deformed and undeformed metric tensors, the computation of the stress tensor 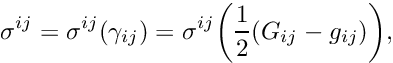$ \sigma^{ij} $ for an incompressible material therefore requires the computation of the following quantities:

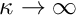
    • The deviatoric stress $ \overline{\sigma}^{ij} $
    • The contravariant deformed metric tensor $ G^{ij} $
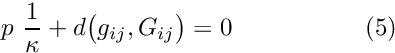
    • The determinant of the deformed metric tensors, 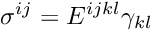$ \det G_{ij}, $ which is required in equation (2) whose solution determines the pressure.


These quantities can be obtained from the following interface

// Deviatoric part of the 2nd Piola Kirchhoff stress tensor
DenseMatrix<double> sigma_dev(DIM,DIM);
// Metric tensor in the undeformed (stress-free) configuration
DenseMatrix<double> g(DIM,DIM);
// Metric tensor in the deformed configuration
DenseMatrix<double> G(DIM,DIM);
// Determinant of the deformed metric tensor
double Gdet;
// Contravariant deformed metric tensor
DenseMatrix<double> G_contra(DIM,DIM);
// Compute stress from the two metric tensors:
calculate_second_piola_kirchhoff_stress(g,G,sigma_dev,G_contra,Gdet);




  1. Nearly Incompressible Behaviour:
    If the material is nearly incompressible, it is advantageous to split the stress into its deviatoric and hydrostatic parts by writing the constitutive law in the form

    \[ \sigma^{ij} = -p G^{ij} + \overline{\sigma}^{ij}\big(\gamma_{kl}\big), \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \]

    where the deviatoric part of the stress tensor, 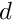$ \overline{\sigma}^{ij}, $ depends on the strain. This form of the constitutive law is identical to that of the incompressible case and it involves a pressure 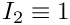$ p $ which needs to be determined from an additional equation. In the incompressible case, this equation was given by the incompressibility constraint (2). Here, we need to augment the constitutive law (3) by a separate equation for the pressure. Generally this takes the form

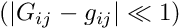    \[ p = - \kappa \ d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \]

    where $ \kappa $ is the "bulk modulus", a material property that needs to be specified by the constitutive law. 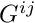$ d $ is the (generalised) dilatation, i.e. the relative change in the volume of an infinitesimal material element (or some suitable generalised quantitiy that is related to it). As the material approaches incompressibility, 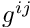$ \kappa \to \infty$, so that infinitely large pressures would be required to achieve any change in volume. To facilitate the implementation of (4) as the equation for the pressure, we re-write it in the form

    \[ p \ \frac{1}{\kappa} + d\big(g_{ij},G_{ij}\big) = 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \]

    which only involves quantities that remain finite as we approach true incompressibility.
    Given the deformed and undeformed metric tensors, the computation of the stress tensor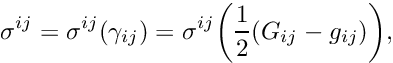 $ \sigma^{ij} $ for a nearly incompressible material therefore requires the computation of the following quantities:

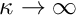
    • The deviatoric stress $ \overline{\sigma}^{ij} $
    • The contravariant deformed metric tensor $ G^{ij} $
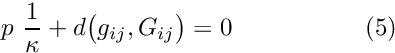
    • The generalised dilatation $ d $
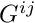
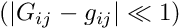
    • The inverse of the bulk modulus $ \kappa $


These quantities can be obtained from the following interface

// Deviatoric part of the 2nd Piola Kirchhoff stress tensor
DenseMatrix<double> sigma_dev(DIM,DIM);
// Metric tensor in the undeformed (stress-free) configuration
DenseMatrix<double> g(DIM,DIM);
// Metric tensor in the deformed configuration
DenseMatrix<double> G(DIM,DIM);
// Contravariant deformed metric tensor
DenseMatrix<double> G_contra(DIM,DIM);
// Inverse of the bulk modulus
double inv_kappa;
// Generalised dilatation
double gen_dil;
// Compute stress from the two metric tensors:
calculate_second_piola_kirchhoff_stress(g,G,sigma_dev,G_contra,inv_kappa,gen_dil);

Definition at line 470 of file constitutive_laws.h.

Constructor & Destructor Documentation

◆ ConstitutiveLaw()

oomph::ConstitutiveLaw::ConstitutiveLaw ( )
inline

Empty constructor.

Definition at line 501 of file constitutive_laws.h.

◆ ~ConstitutiveLaw()

virtual oomph::ConstitutiveLaw::~ConstitutiveLaw ( )
inlinevirtual

Empty virtual destructor.

Definition at line 505 of file constitutive_laws.h.

Member Function Documentation

◆ are_matrices_of_equal_dimensions()

bool oomph::ConstitutiveLaw::are_matrices_of_equal_dimensions ( const DenseMatrix< double > &  M1,
const DenseMatrix< double > &  M2 
)
protected

Test whether two matrices are of equal dimensions.

This function is used to check whether matrices are of equal dimension.

Definition at line 52 of file constitutive_laws.cc.

References oomph::DenseMatrix< T >::ncol(), and oomph::DenseMatrix< T >::nrow().

Referenced by calculate_contravariant(), calculate_d_second_piola_kirchhoff_stress_dG(), and error_checking_in_input().

◆ calculate_contravariant()

double oomph::ConstitutiveLaw::calculate_contravariant ( const DenseMatrix< double > &  Gcov,
DenseMatrix< double > &  Gcontra 
)
protected

Calculate a contravariant tensor from a covariant tensor, and return the determinant of the covariant tensor.

The function to calculate the contravariant tensor from a covariant one.

Three dimensions

Definition at line 113 of file constitutive_laws.cc.

References are_matrices_of_equal_dimensions(), is_matrix_square(), oomph::DenseMatrix< T >::ncol(), and oomph::Global_string_for_annotation::string().

Referenced by oomph::GeneralisedHookean::calculate_second_piola_kirchhoff_stress(), and oomph::IsotropicStrainEnergyFunctionConstitutiveLaw::calculate_second_piola_kirchhoff_stress().

◆ calculate_d_contravariant_dG()

void oomph::ConstitutiveLaw::calculate_d_contravariant_dG ( const DenseMatrix< double > &  Gcov,
RankFourTensor< double > &  dGcontra_dG,
DenseMatrix< double > &  d_detG_dG 
)
protected

Calculate the derivatives of the contravariant tensor and the derivatives of the determinant of the covariant tensor with respect to the components of the covariant tensor.

The function to calculate the derivatives of the contravariant tensor and determinant of covariant tensor with respect to the components of the covariant tensor.

Three dimensions

Definition at line 225 of file constitutive_laws.cc.

References is_matrix_square(), oomph::DenseMatrix< T >::ncol(), and oomph::Global_string_for_annotation::string().

◆ calculate_d_second_piola_kirchhoff_stress_dG() [1/3]

void oomph::ConstitutiveLaw::calculate_d_second_piola_kirchhoff_stress_dG ( const DenseMatrix< double > &  g,
const DenseMatrix< double > &  G,
const DenseMatrix< double > &  sigma,
const double &  detG,
const double &  interpolated_solid_p,
RankFourTensor< double > &  d_sigma_dG,
DenseMatrix< double > &  d_detG_dG,
const bool &  symmetrize_tensor = true 
)
virtual

Calculate the derivatives of the contravariant 2nd Piola Kirchhoff stress tensor $ \sigma^{ij}$. with respect to the deformed metric tensor. Also return the derivatives of the determinant of the deformed metric tensor with respect to the deformed metric tensor. This form is appropriate for truly-incompressible materials. The default implementation uses finite differences for the derivatives that depend on the constitutive law, but not for the derivatives of the determinant, which are generic. / If the boolean flag symmetrize_tensor is false, only the "upper triangular" entries of the tensor will be filled in. This is a useful efficiency when using the derivatives in Jacobian calculations.

Calculate the derivatives of the contravariant 2nd Piola Kirchhoff stress tensor $ \sigma^{ij}$. with respect to the deformed metric tensor. Also return the derivatives of the determinant of the deformed metric tensor with respect to the deformed metric tensor. This form is appropriate for truly-incompressible materials. The default implementation uses finite differences for the derivatives that depend on the constitutive law, but not for the derivatives of the determinant, which are generic.

Definition at line 453 of file constitutive_laws.cc.

References are_matrices_of_equal_dimensions(), calculate_second_piola_kirchhoff_stress(), oomph::GeneralisedElement::Default_fd_jacobian_step, i, and oomph::DenseMatrix< T >::ncol().

◆ calculate_d_second_piola_kirchhoff_stress_dG() [2/3]

void oomph::ConstitutiveLaw::calculate_d_second_piola_kirchhoff_stress_dG ( const DenseMatrix< double > &  g,
const DenseMatrix< double > &  G,
const DenseMatrix< double > &  sigma,
const double &  gen_dil,
const double &  inv_kappa,
const double &  interpolated_solid_p,
RankFourTensor< double > &  d_sigma_dG,
DenseMatrix< double > &  d_gen_dil_dG,
const bool &  symmetrize_tensor = true 
)
virtual

Calculate the derivatives of the contravariant 2nd Piola Kirchoff stress tensor with respect to the deformed metric tensor. Also return the derivatives of the generalised dilatation, $ d, $ with respect to the deformed metric tensor. This form is appropriate for near-incompressible materials. The default implementation uses finite differences. If the boolean flag symmetrize_tensor is false, only the "upper triangular" entries of the tensor will be filled in. This is a useful efficiency when using the derivatives in Jacobian calculations.

Calculate the derivatives of the contravariant 2nd Piola Kirchoff stress tensor with respect to the deformed metric tensor. Also return the derivatives of the generalised dilatation, $ d, $ with respect to the deformed metric tensor. This form is appropriate for near-incompressible materials. The default implementation uses finite differences.

Definition at line 566 of file constitutive_laws.cc.

References are_matrices_of_equal_dimensions(), calculate_second_piola_kirchhoff_stress(), oomph::GeneralisedElement::Default_fd_jacobian_step, i, and oomph::DenseMatrix< T >::ncol().

◆ calculate_d_second_piola_kirchhoff_stress_dG() [3/3]

void oomph::ConstitutiveLaw::calculate_d_second_piola_kirchhoff_stress_dG ( const DenseMatrix< double > &  g,
const DenseMatrix< double > &  G,
const DenseMatrix< double > &  sigma,
RankFourTensor< double > &  d_sigma_dG,
const bool &  symmetrize_tensor = true 
)
virtual

Calculate the derivatives of the contravariant 2nd Piola Kirchhoff stress tensor with respect to the deformed metric tensor. Arguments are the covariant undeformed and deformed metric tensor, the current value of the stress tensor and the rank four tensor in which to return the derivatives of the stress tensor The default implementation uses finite differences, but can be overloaded for constitutive laws in which an analytic formulation is possible. If the boolean flag symmetrize_tensor is false, only the "upper triangular" entries of the tensor will be filled in. This is a useful efficiency when using the derivatives in Jacobian calculations.

Calculate the derivatives of the contravariant 2nd Piola Kirchhoff stress tensor with respect to the deformed metric tensor. Arguments are the covariant undeformed and deformed metric tensor and the matrix in which to return the derivatives of the stress tensor The default implementation uses finite differences, but can be overloaded for constitutive laws in which an analytic formulation is possible.

Definition at line 352 of file constitutive_laws.cc.

References are_matrices_of_equal_dimensions(), calculate_second_piola_kirchhoff_stress(), oomph::GeneralisedElement::Default_fd_jacobian_step, i, and oomph::DenseMatrix< T >::ncol().

Referenced by oomph::PVDEquationsWithPressure< DIM >::get_d_stress_dG_upper(), and oomph::PVDEquations< DIM >::get_d_stress_dG_upper().

◆ calculate_second_piola_kirchhoff_stress() [1/3]

virtual void oomph::ConstitutiveLaw::calculate_second_piola_kirchhoff_stress ( const DenseMatrix< double > &  g,
const DenseMatrix< double > &  G,
DenseMatrix< double > &  sigma 
)
pure virtual

Calculate the contravariant 2nd Piola Kirchhoff stress tensor. Arguments are the covariant undeformed and deformed metric tensor and the matrix in which to return the stress tensor.

Implemented in oomph::IsotropicStrainEnergyFunctionConstitutiveLaw, and oomph::GeneralisedHookean.

Referenced by calculate_d_second_piola_kirchhoff_stress_dG(), oomph::AxisymmetricPVDEquations::get_stress(), oomph::PVDEquations< DIM >::get_stress(), oomph::AxisymmetricPVDEquationsWithPressure::get_stress(), and oomph::PVDEquationsWithPressure< DIM >::get_stress().

◆ calculate_second_piola_kirchhoff_stress() [2/3]

virtual void oomph::ConstitutiveLaw::calculate_second_piola_kirchhoff_stress ( const DenseMatrix< double > &  g,
const DenseMatrix< double > &  G,
DenseMatrix< double > &  sigma_dev,
DenseMatrix< double > &  G_contra,
double &  Gdet 
)
inlinevirtual

Calculate the deviatoric part $ \overline{ \sigma^{ij}}$ of the contravariant 2nd Piola Kirchhoff stress tensor $ \sigma^{ij}$. Also return the contravariant deformed metric tensor and the determinant of the deformed metric tensor. This form is appropriate for truly-incompressible materials for which $ \sigma^{ij} = - p G^{ij} +\overline{ \sigma^{ij}} $ where the "pressure" $ p $ is determined by $ \det G_{ij} - \det g_{ij} = 0 $.

Reimplemented in oomph::IsotropicStrainEnergyFunctionConstitutiveLaw, and oomph::GeneralisedHookean.

Definition at line 547 of file constitutive_laws.h.

◆ calculate_second_piola_kirchhoff_stress() [3/3]

virtual void oomph::ConstitutiveLaw::calculate_second_piola_kirchhoff_stress ( const DenseMatrix< double > &  g,
const DenseMatrix< double > &  G,
DenseMatrix< double > &  sigma_dev,
DenseMatrix< double > &  Gcontra,
double &  gen_dil,
double &  inv_kappa 
)
inlinevirtual

Calculate the deviatoric part of the contravariant 2nd Piola Kirchoff stress tensor. Also return the contravariant deformed metric tensor, the generalised dilatation, $ d, $ and the inverse of the bulk modulus $ \kappa$. This form is appropriate for near-incompressible materials for which $ \sigma^{ij} = -p G^{ij} + \overline{ \sigma^{ij}} $ where the "pressure" $ p $ is determined from $ p / \kappa - d =0 $.

Reimplemented in oomph::IsotropicStrainEnergyFunctionConstitutiveLaw, and oomph::GeneralisedHookean.

Definition at line 592 of file constitutive_laws.h.

◆ error_checking_in_input()

void oomph::ConstitutiveLaw::error_checking_in_input ( const DenseMatrix< double > &  g,
const DenseMatrix< double > &  G,
DenseMatrix< double > &  sigma 
)
protected

Check for errors in the input, i.e. check that the dimensions of the arrays are all consistent.

This function is used to provide simple error (bounce) checks on the input to any calculate_second_piola_kirchhoff_stress.

Definition at line 71 of file constitutive_laws.cc.

References are_matrices_of_equal_dimensions(), is_matrix_square(), and oomph::Global_string_for_annotation::string().

Referenced by oomph::GeneralisedHookean::calculate_second_piola_kirchhoff_stress(), and oomph::IsotropicStrainEnergyFunctionConstitutiveLaw::calculate_second_piola_kirchhoff_stress().

◆ is_matrix_square()

bool oomph::ConstitutiveLaw::is_matrix_square ( const DenseMatrix< double > &  M)
protected

Test whether a matrix is square.

This function is used to check whether a matrix is square.

Definition at line 36 of file constitutive_laws.cc.

References oomph::DenseMatrix< T >::ncol(), and oomph::DenseMatrix< T >::nrow().

Referenced by calculate_contravariant(), calculate_d_contravariant_dG(), and error_checking_in_input().

◆ requires_incompressibility_constraint()

virtual bool oomph::ConstitutiveLaw::requires_incompressibility_constraint ( )
pure virtual

Pure virtual function in which the user must declare if the constitutive equation requires an incompressible formulation in which the volume constraint is enforced explicitly. Used as a sanity check in PARANOID mode.

Implemented in oomph::IsotropicStrainEnergyFunctionConstitutiveLaw, and oomph::GeneralisedHookean.

Referenced by oomph::RefineablePVDEquations< DIM >::fill_in_generic_contribution_to_residuals_pvd(), oomph::PVDEquations< DIM >::fill_in_generic_contribution_to_residuals_pvd(), oomph::RefineablePVDEquationsWithPressure< DIM >::fill_in_generic_residual_contribution_pvd_with_pressure(), and oomph::PVDEquationsWithPressure< DIM >::fill_in_generic_residual_contribution_pvd_with_pressure().

The documentation for this class was generated from the following files: