In this document we show how to add internal boundaries and create connections among them in 2D unstructured meshes with oomph-lib. The mesh generation procedure is performed by using Jonathan Shewchuk's Triangle. This tutorial complements the discussion in another tutorial where we illustrated how to build oomph-lib meshes using the TriangleMeshPolygon and TriangleMeshClosedCurve objects.

Additionally, we show via examples

how to connect TriangleMeshCurveSection objects
how to add addition holes and extra regions, i.e. regions not defined via TriangleMeshPolygon or TriangleMeshClosedCurve objects

Adding internal boundaries

The TriangleMeshOpenCurve object

An internal boundary is defined in oomph-lib by the object TriangleMeshOpenCurve. We can create and add as many internal boundaries as we need for defining our domain, see figure below.

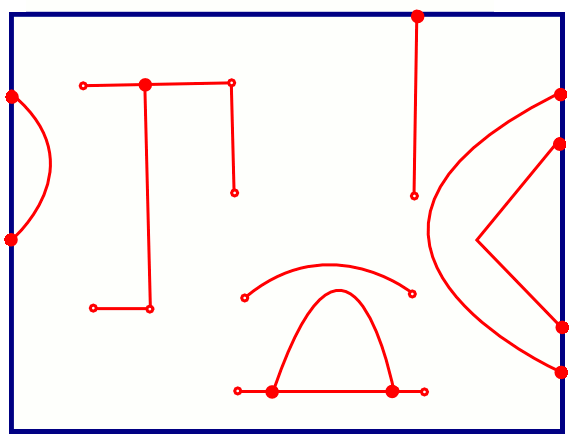
The TriangleMeshOpenCurve object allow us to define domains with internal boundaries. The internal boundaries are shown in red. Notice the connections of the internal boundaries with other boundaries. The connections are shown with filled small circles.

The TriangleMeshOpenCurve object allows the creation of complex internal boundaries as a combination of TriangleMeshPolyLine and/or TriangleMeshCurviLine objects. In order to create a TriangleMeshOpenCurve it is necessary to create a Vector of TriangleMeshCurveSection objects that define the TriangleMeshOpenCurve, see figure below.

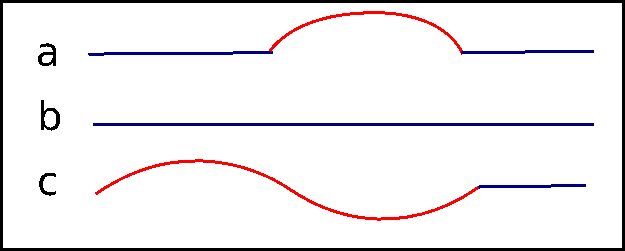
Different types of TriangleMeshOpenCurve, a) A TriangleMeshOpenCurve defined as a combination of two TriangleMeshPolyLines (in blue) and a TriangleMeshCurviLine (in red). b) A TriangleMeshOpenCurve can also be defined as just one TriangleMeshCurveSection, in this case a TriangleMeshPolyLine. c) A TriangleMeshOpenCurve defined as a combination of a TriangleMeshPolyLine and a TrianglesMeshCurviLine.

Creating connections among current boundaries in the domain and with internal boundaries

Any internal boundary can be connected (via its ends) to any other boundary currently in the domain.

It is important to note that there are four different types of connections:

Connection between a TriangleMeshPolyLine and a TriangleMeshPolyLine
Connection between a TriangleMeshCurviLine and a TriangleMeshPolyLine
Connection between a TriangleMeshPolyLine and a TriangleMeshCurviLine
Connection between a TriangleMeshCurviLine and a TriangleMeshCurviLine

The next figure shows an sketch of the different types of connections.

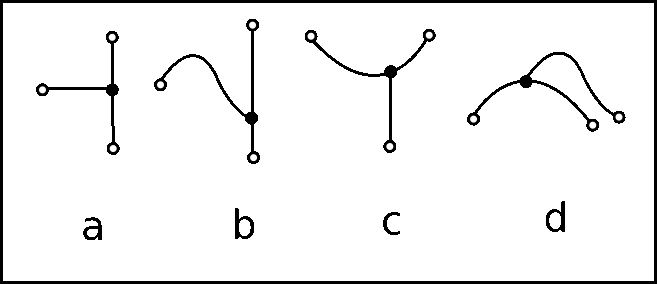
Different types of connections. a) Connection between a TriangleMeshPolyLine and a TriangleMeshPolyLine. b) Connection between a TriangleMeshCurviLine and a TriangleMeshPolyLine. c) Connection between a TriangleMeshPolyLine and a TriangleMeshCurviLine. d) Connection between a TriangleMeshCurviLine and a TriangleMeshCurviLine.

Connections to TriangleMeshPolyLine can only be made by using existing vertices of the destination TriangleMeshPolyLine. Conversely, connections to TriangleMeshCurviLine can be made by specifying the position along the TriangleMeshCurviLine. The
connection point is identified by the TriangleMeshCurviLine's intrinsic coordinates. The figure below shows the case when a connection with a TriangleMeshPolyLine is possible.

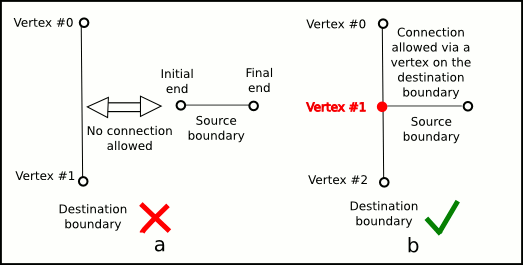
In order to connect a boundary to a TriangleMeshPolyLine it is necessary that the destination boundary has a vertex on the connection point. a) There is no vertex for connecting to the destination TriangleMeshPolyLine. b) There is a vertex in the destination TriangleMeshPolyLine to receive the initial end of the source boundary.

Example: A domain with multiple internal boundaries and connections

We will show how to add internal boundaries and how to create connections among them by using the same example as in another tutorial.

A sketch of the domain is shown on the next figure. The domain has seven boundaries, two of which define the outer boundary and the other five define internal boundaries.

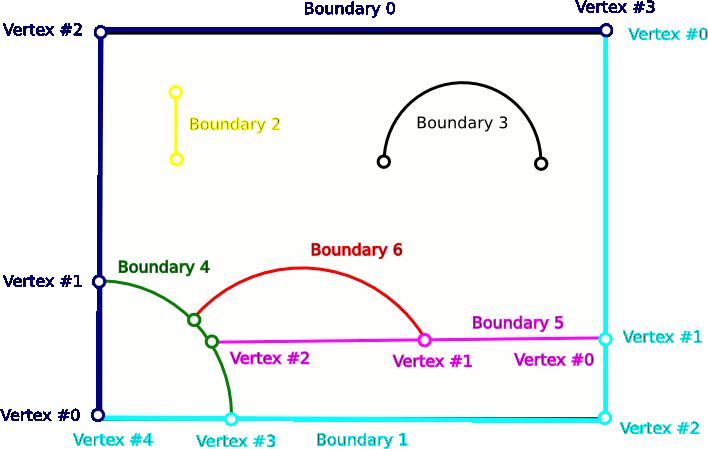
The sketch of the domain; note the different internal boundaries and their connection points.

Definition of the domain/mesh

The following code is extracted from the Problem constructor and shows how to create the domain/mesh.

Defining the outer boundaries

The first task is to define the outer boundary which we represent by a TriangleMeshClosedCurve comprising two TriangleMeshPolyLines.

  // Begin - Outer boundary
 
  // Create storage for the vertices coordinates that define each boundary
  const unsigned num_vertices_b0 = 4;
  Vector<Vector <double> > vertices(num_vertices_b0);
 
  vertices[0].resize(2);
  vertices[1].resize(2);
  vertices[2].resize(2);
  vertices[3].resize(2);
 
  // Building the outer boundary (vertices)
  vertices[0][0] = 0;
  vertices[0][1] = 0;
 
  vertices[1][0] = 0;
  vertices[1][1] = 1;
 
  vertices[2][0] = 0;
  vertices[2][1] = 3;
 
  vertices[3][0] = 3;
  vertices[3][1] = 3;
 
  // The outer boundary is represented by two TriangleMeshPolyLine objects,
  // this is the first one
  boundary_id = 0;
  TriangleMeshPolyLine *boundary0_pt =
      new TriangleMeshPolyLine(vertices, boundary_id);
 
  // Create storage for the vertices coordinates that define each boundary
  const unsigned num_vertices_b1 = 5;
  vertices.resize(num_vertices_b1);
 
  vertices[0].resize(2);
  vertices[1].resize(2);
  vertices[2].resize(2);
  vertices[3].resize(2);
  vertices[4].resize(2);
 
  // More vertices for the outer boundary
  vertices[0][0] = 3;
  vertices[0][1] = 3;
 
  vertices[1][0] = 3;
  vertices[1][1] = 0.5;
 
  vertices[2][0] = 3;
  vertices[2][1] = 0;
 
  vertices[3][0] = 1;
  vertices[3][1] = 0;
 
  vertices[4][0] = 0;
  vertices[4][1] = 0;
 
  // The outer boundary is represented by two TriangleMeshPolyLine objects,
  // this is the second one
  boundary_id = 1;
  TriangleMeshPolyLine *boundary1_pt =
      new TriangleMeshPolyLine(vertices, boundary_id);
 
  // A vector for storing the outer boundary representation
  Vector<TriangleMeshCurveSection*> outer_boundary_polyLines_pt(2);
 
  outer_boundary_polyLines_pt[0] = boundary0_pt;
  outer_boundary_polyLines_pt[1] = boundary1_pt;
 
  TriangleMeshClosedCurve *outer_boundary_pt =
      new TriangleMeshPolygon(outer_boundary_polyLines_pt);
  // End - Outer boundary

Note that we defined additional vertices along the two boundaries to allow the creation of connections to the outer boundary, see figure below.

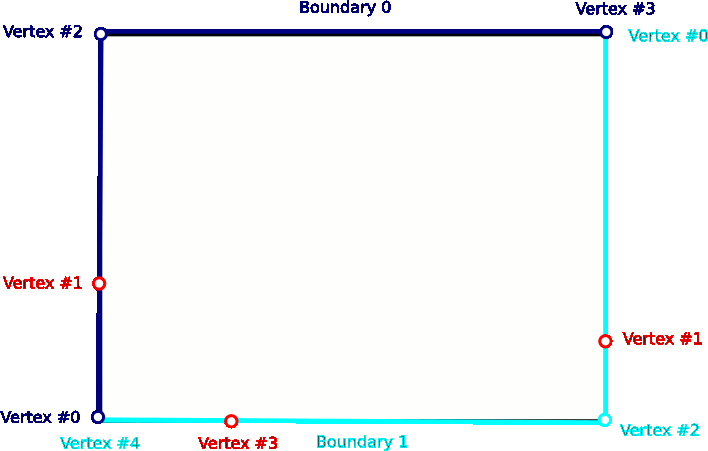
Vertex 1 on boundary 0 and vertices 1 and 3 on boundary 1 are created to allow the subsequent connections with internal boundaries.

Defining internal boundaries

We create a Vector of five TriangleMeshOpenCurves which will represent the internal boundaries.

  // Internal open boundaries
  // Total number of open curves in the domain
  unsigned n_open_curves = 5;
 
  // We want internal open curves
  Vector<TriangleMeshOpenCurve *> inner_open_boundaries_pt(n_open_curves);

Simple internal boundaries without connections

Our domain has two unconnected internal boundaries: a straight line, represented by a TriangleMeshPolyLine and a curve line represented by a TriangleMeshCurviLine.

  // We start by creating the internal boundaries
  // The boundary 2 is defined by its two vertices
  // Open curve 1
  vertices.resize(2);
  vertices[0].resize(2);
  vertices[1].resize(2);
 
  vertices[0][0] = 0.5;
  vertices[0][1] = 2.0;
 
  vertices[1][0] = 0.5;
  vertices[1][1] = 2.5;
 
  boundary_id = 2;
  TriangleMeshPolyLine *boundary2_pt =
    new TriangleMeshPolyLine(vertices, boundary_id);
 
  // Each internal open curve is defined by a vector of TriangleMeshCurveSection,
  // on this example we only need one curve section for each internal boundary
  Vector<TriangleMeshCurveSection *> internal_curve_section1_pt(1);
 
  internal_curve_section1_pt[0] = boundary2_pt;
 
  // The open curve that define this boundary is composed of just one
  // curve section
  inner_open_boundaries_pt[0] =
      new TriangleMeshOpenCurve(internal_curve_section1_pt);
 
  // *********************************************************************
  // We define the curved boundary as a TriangleMeshCurviline
  // Open curve 2
  double x_centre = 2.0;
  double y_centre = 2.0;
  double r_circle = 0.5;
 
  Circle * boundary_circle1_pt = new Circle(x_centre, y_centre, r_circle);
 
  // Number of segments used for representing the curve boundary
  unsigned n_segments = 20;
 
  // The intrinsic coordinates for the beginning and end of the curve
  double s_start = 0.0;
  double s_end = MathematicalConstants::Pi;
 
  boundary_id = 3;
  TriangleMeshCurviLine *boundary3_pt =
      new TriangleMeshCurviLine(boundary_circle1_pt,
          s_start,
          s_end,
          n_segments,
          boundary_id);
 
  Vector<TriangleMeshCurveSection *> internal_curve_section2_pt(1);
  internal_curve_section2_pt[0] = boundary3_pt;
 
  // The open curve that define this boundary is composed of just one
  // curve section
  inner_open_boundaries_pt[1] =
      new TriangleMeshOpenCurve(internal_curve_section2_pt);

Adding an internal boundary connected to an outer boundary

We need to add three more internal boundaries which have connections with the outer boundary and with some internal boundaries; see the sketch of the domain.

In order to connect an internal boundary with any other boundary in the domain it is necessary to specify the following:

Is the initial or the final end of the boundary the one that we want to connect?
Do we want to connect the boundary with a TriangleMeshPolyLine or with a TriangleMeshCurviLine?
If we want to connect with a TriangleMeshPolyLine then we need to identify the corresponding vertex number to which we want to connect. If we want to connect with a TriangleMeshCurviLine we need to identify the corresponding intrinsic coordinate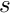 on the curve for connection.

Consider the creation of the internal boundary 4 shown on the sketch of the domain. This is an example of connecting a TriangleMeshCurviLine with a TriangleMeshPolyLine (the outer boundary). In this case both ends of the TriangleMeshCurviLine are connected so we need to use the interface for connecting the initial and the final ends of the boundary to a TriangleMeshPolyLine. There is only one thing left to identify, the vertex number of the destination boundary to which we want to connect. By looking at figure 1.5 we see that these values are vertex #3 for the initial end and vertex #1 for the final end. Once identified, we perform the connection as follow:

Create the internal boundary as usual

  // Open curve 3
  x_centre = 0.0;
  y_centre = 0.0;
  r_circle = 1.0;
 
  Circle * boundary_circle2_pt = new Circle(x_centre, y_centre, r_circle);
 
  // Number of segments used for representing the curve boundary
  n_segments = 20;
 
  // The intrinsic coordinates for the beginning and end of the curve
  s_start = 0.0;
  s_end = MathematicalConstants::Pi / 2.0;
 
  // State the vertex number for connection on the destination
  // boundaries
  unsigned vertex_to_connect_initial = 3;
  unsigned vertex_to_connect_final = 1;
 
  boundary_id = 4;
  TriangleMeshCurviLine *boundary4_pt =
      new TriangleMeshCurviLine(boundary_circle2_pt,
          s_start,
          s_end,
          n_segments,
          boundary_id);

Specify connections using the destination boundary and the vertex number

  // Do the connection with the destination boundary, in this case
  // the connection is done with the outer boundary
  boundary4_pt->connect_initial_vertex_to_polyline(
                                boundary1_pt,
                                vertex_to_connect_initial);
 
  // Do the connection with the destination boundary, in this case
  // the connection is done with the outer boundary
  boundary4_pt->connect_final_vertex_to_polyline(
                                boundary0_pt,
                                vertex_to_connect_final);

Finally, create the TriangleMeshOpenCurve object as usual

  // The open curve that define this boundary is composed of just one
  // curve section
  inner_open_boundaries_pt[2] =
      new TriangleMeshOpenCurve(internal_curve_section3_pt);

Adding an internal boundary connected with another internal boundary

Boundary 5, a straight line connected to the outer boundary and to an internal boundary (the one that we created on the previous step).

The initial end of the boundary is connected to the outer boundary therefore we need to identify the vertex number to which it is connected; by looking at the sketch of the domain we see that the destination vertex number is 1. The final end is connected with a TriangleMeshCurviLine therefore we need to specify the intrinsic coordinate in the object where we want to connect (the intrinsic coordinate is the arc-length along the circle).

  // This boundary is connected to the outer boundary on the initial end
  // and to an internal boundary on the final end
  // Open curve 4
  vertices.resize(3);
  vertices[0].resize(2);
  vertices[1].resize(2);
  vertices[2].resize(2);
 
  // We need to specify the vertices for the boundary on the first end
  // The connection method performs a checking on the matching of the
  // vertices used for connection
  vertices[0][0] = 3.0;
  vertices[0][1] = 0.5;
 
  // These values are necessary when we subsequently perform the connection
  // of the last boundary
  vertices[1][0] = (3.0 + sqrt(3.0)) * 0.5;
  vertices[1][1] = 0.5;
 
  // We need to specify the vertices for the boundary on the last end
  // The connection method performs a checking on the matching of the
  // vertices used for connection
  vertices[2][0] = sqrt(3.0) * 0.5;
  vertices[2][1] = 0.5;
 
  // State the vertex number for connection with the destination
  // boundary
  vertex_to_connect_initial = 1;
 
  // State the s value for connection with the destination boundary
  double s_connection_final = atan2(0.5, sqrt(3.0) * 0.5);
 
  boundary_id = 5;
  TriangleMeshPolyLine *boundary5_pt =
    new TriangleMeshPolyLine(vertices, boundary_id);
 
  // Do the connection with the destination boundary, in this case
  // the connection is done with the outer boundary
  boundary5_pt->connect_initial_vertex_to_polyline(
                                boundary1_pt,
                                vertex_to_connect_initial);
 
  // Do the connection with the destination boundary, in this case
  // the connection is done with an internal boundary
  boundary5_pt->connect_final_vertex_to_curviline(
                                boundary4_pt,
                                s_connection_final);
 
  Vector<TriangleMeshCurveSection *> internal_curve_section4_pt(1);
  internal_curve_section4_pt[0] = boundary5_pt;
 
  // The open curve that define this boundary is composed of just one
  // curve section
  inner_open_boundaries_pt[3] =
      new TriangleMeshOpenCurve(internal_curve_section4_pt);

Adding an internal boundary connected with another internal boundary (the last one from our example)

The fifth internal boundary is connected to two internal boundaries. The initial end of the new internal boundary is connected to a TriangleMeshPolyLine and the final end is connected to a TriangleMeshCurviLine. The vertex number for connection with the TriangleMeshPolyLine was established in the definition of the previous internal boundary, vertex #1. The circles defining boundaries 4 and 6 meet each other at $(x, y) = (\frac{3}{4}, \frac{\sqrt(7)}{4})$ which corresponds to the intrinsic coordinate $s = arctan(\frac{\sqrt{7}}{3})$ on the TriangleMeshCurviLine object representing boundary 4.

  // Open curve 5
  x_centre = 1.5;
  y_centre = 0.0;
  r_circle = 1.0;
 
  Circle * boundary_circle3_pt = new Circle(x_centre, y_centre, r_circle);
 
  // Number of segments used for representing the curve boundary
  n_segments = 20;
 
  // These numbers can be easily obtained by computing the
  // intersection of the circle (circle3) and the other boundaries
  // (in this case, boundaries 4 and 5)
  s_start = atan2(0.5, (3.0 + sqrt(3.0)) * 0.5 - 1.5);
  s_end = atan2(0.25*sqrt(7.0), -0.75);
 
  // State the vertex number for connection on the destination
  // boundaries
  vertex_to_connect_initial = 1;
 
  // State the s value for connection with the destination boundary
  s_connection_final = atan2(0.25*sqrt(7.0), 0.75);
 
  boundary_id = 6;
  TriangleMeshCurviLine *boundary6_pt =
    new TriangleMeshCurviLine(boundary_circle3_pt,
          s_start,
          s_end,
          n_segments,
          boundary_id);
 
  // Do the connection with the destination boundary, in this case
  // the connection is done with an internal boundary
  boundary6_pt->connect_initial_vertex_to_polyline(
                                boundary5_pt,
                                vertex_to_connect_initial);
 
  // Do the connection with the destination boundary, in this case
  // the connection is done with an internal boundary
  boundary6_pt->connect_final_vertex_to_curviline(
                                boundary4_pt,
                                s_connection_final);
 
  Vector<TriangleMeshCurveSection *> internal_curve_section5_pt(1);
  internal_curve_section5_pt[0] = boundary6_pt;
 
  // The open curve that define this boundary is composed of just one
  // curve section
  inner_open_boundaries_pt[4] =
      new TriangleMeshOpenCurve(internal_curve_section5_pt);

Build the mesh

We build the mesh specific parameters using a TriangleMeshParameters object.

  //Create mesh
 
  // Use the TriangleMeshParameters object for helping on the manage of the
  // TriangleMesh parameters. The only parameter that needs to take is the
  // outer boundary.
  TriangleMeshParameters triangle_mesh_parameters(outer_boundary_pt);
 
  // Specify the internal closed boundaries
  triangle_mesh_parameters.internal_closed_curve_pt() = inner_boundaries_pt;
 
  // Specify the internal open boundaries
  triangle_mesh_parameters.internal_open_curves_pt() = inner_open_boundaries_pt;
 
  // One can define an specific maximum element area
  double element_area = 0.2;
  triangle_mesh_parameters.element_area() = element_area;
 
  // Pass the TriangleMeshParameters object to the TriangleMesh one
  Problem::mesh_pt() = new TriangleMesh<ELEMENT>(triangle_mesh_parameters);

Defining additional holes and regions

It is possible to define holes in the domain using the methods discussed in another tutorial; where we explained how to create holes by using closed curves. Holes could also be created by specifying additional parameters on the TriangleMeshParameters object. The specification of regions or layers follows the same principle.

Defining additional holes

For defining holes it is only necessary to specify a point that lies inside a closed boundary (created by the connection of internal open boundaries). For example, the region bounded by boundaries 4, 5 and 6 can be turned into a hole by specifying the coordinate , see figure below.

The sketch of the domain with a hole created by the connection of internal lines.

  // Adding a hole on the domain
  Vector<Vector <double> > additional_hole(1);
 
  // Define the coordinates on the domain
  additional_hole[0].resize(2);
  additional_hole[0][0] = 1.5;
  additional_hole[0][1] = 0.75;
 
  // Pass information about the additional holes coordinates
  triangle_mesh_parameters.extra_holes_coordinates() = additional_hole;
  // Pass the TriangleMeshParameters object to the TriangleMesh one
  Problem::mesh_pt() = new TriangleMesh<ELEMENT>(triangle_mesh_parameters);

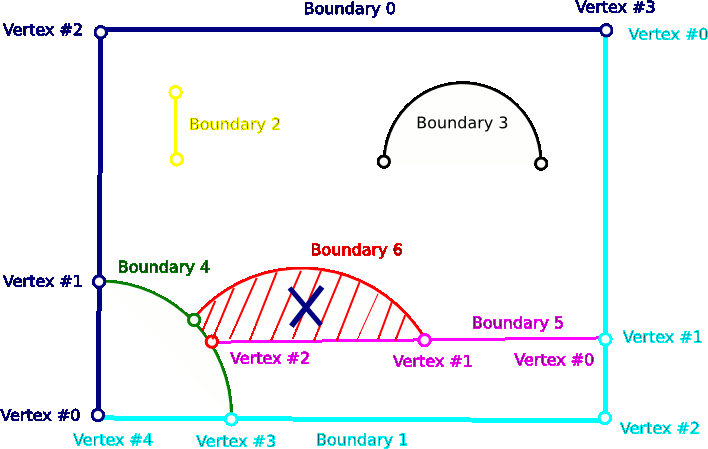
Defining regions

The definition of regions follows the same principle that defining holes, it means, one only need to specify the coordinates of a point that lies inside a region. If we would like to define the region showed on light grey on the figure below we use the method add_region_coordinates of the TriangleMeshParameters object. You can specify any region id for the defined region.

The sketch of the domain with a hole and a defined region.

  // Adding a region on the domain
  Vector<double> region(2);
 
  // Define the coordinates of the regions on the domain
  region[0] = 0.5;
  region[1] = 0.5;
 
  // Pass information about the defined regions
  triangle_mesh_parameters.add_region_coordinates(1, region);
  
  // Specify different target area of region 1:
  triangle_mesh_parameters.set_target_area_for_region(1,0.01);
 
  // Pass the TriangleMeshParameters object to the TriangleMesh one
  Problem::mesh_pt() = new TriangleMesh<ELEMENT>(triangle_mesh_parameters);

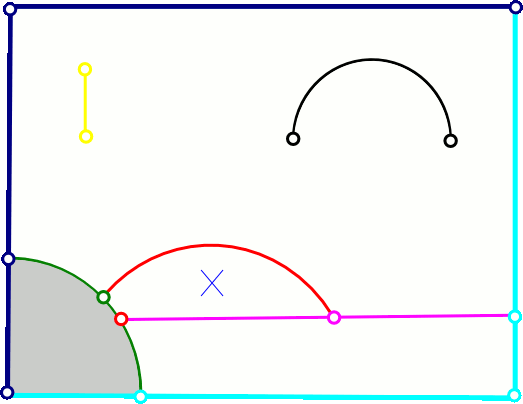
By default the complete domain belongs to region zero. Therefore, one could leave parts of the domain without a defined region or explicitly define all the regions on the domain. NOTE: Be sure to use the region ids when documenting the solution by its specified regions.

Comments and exercises

Create two new internal boundaries without connections, one using a TriangleMeshPolyLine object and other using a TriangleMeshCurviLine object.
Define a new vertex on the new TriangleMeshPolyLine and create a connection to that vertex.
Once one performs a connection to a TriangleMeshPolyLine or to a TriangleMeshCurviLine there is an internal checking on the connection vertices coordinates for the TriangleMeshPolyLine and on the connection intrinsic coordinate for the TriangleMesheCurviline case, they must be close enough in order to allow the connection. The tolerance values are tolerance_for_vertex_connection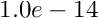 = for the TriangleMeshPolyline case and tolerance_for_zeta_connection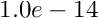 = for the TriangleMeshCurviline case. One can explicitly define the allowed tolerance by adding an extra argument when using the methods connect_initial_vertex_to_polyline, connect_final_vertex_to_polyline connect_initial_vertex_to_curviline or connect_final_vertex_to_curviline. As an exercise, use different values for the allowed connection tolerance.

Source files for this tutorial

The source files for this tutorial are located in the directory:

demo_drivers/meshing/mesh_from_inline_triangle_internal_boundaries/
The driver code is:

demo_drivers/meshing/mesh_from_inline_triangle/mesh_from_inline_triangle_internal_boundaries.cc
The additional driver code

demo_drivers/meshing/mesh_from_inline_triangle_internal_boundaries/mesh_from_inline_triangle_internal_boundaries_extra.cc
shows how to define a hole by connecting internal boundaries.

PDF file

A pdf version of this document is available.