Demo problem: The (axisymmetric) static free surface bounding a layer of viscous fluid.

Overview of the problem

We consider an open circular container of unit radius containing a still viscous fluid of prescribed volume $ \mathcal{V} $ that meets the wall of the container at a contact angle $ \theta_{c} $. The problem is extremely similar to that described in the
two-dimensional static cap tutorial. The exact solution corresponds to a free surface of constant curvature that is the arc of a circle rotated about the axis to give a section of a sphere. The mean curvature of the interface in this problem is $ \kappa = 2/r = 4\cos\theta_{c} $, which differs from the two-dimensional problem in which it was $ 2\cos\theta_{c} $.

The only differences between the axisymmetric and the two-dimensional driver codes are that:

  1. two-dimensional elements are replaced by the equivalent axisymmetric elements;
  2. specified volume is different;
  3. swirl (theta) component of velocity is pinned;
  4. analytic pressure drop is changed.

In other words we make the following changes:

Two-dimensional problem Axisymmetric problem
Bulk Fluid Element QCrouzeixRaviartElement<2> AxisymmetricQCrouzeixRaviartElement
Pseudo-Solid Free Surface Face Element ElasticLineFluidInterfaceElement ElasticAxisymmetricFluidInterfaceElement
Spine Free Surface Face Element SpineLineFluidInterfaceElement SpineAxisymmetricFluidInterfaceElement
Pseudo-Solid Volume Constraint Face Element ElasticLineVolumeConstraintBoundingElement ElasticAxisymmetricVolumeConstraintBoundingElement
Spine Volume Constraint Face Element SpineLineVolumeConstraintBoundingElement SpineAxisymmetricVolumeConstraintBoundingElement
Specific Volume $ x h = 0.5 $ $ r^{2} h /2 = 0.125 $
Analytic pressure drop $ 2\cos\theta_{c} $ $ 4\cos\theta_{c} $

Comments and Exercises

Comments

  • The formula for the specified volume in the axisymmetric case is the true volume 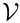$ \mathcal{V} $ divided by 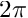$ 2\pi $ because all the axisymmetric equations are divided by the common factor of 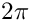$ 2 \pi $. The AxisymmetricVolumeConstraintBoundingElement class must be used so that the volume is correctly calculated.
  • The swirl velocity is pinned on the boundaries by including the additional code
    Bulk_mesh_pt->boundary_node_pt(b,n)->pin(2);

Exercises

  1. Confirm that the computed pressure differences agree with the analytic expression. Verify that the interface shape is unaffected by the capillary number, but that the pressure difference across the interface changes in inverse proportion to it. Check that the pressure difference is unaffected by the choice of reference pressure.

  2. Investigate what happens when the two-dimensional volume constraint elements are used. Explain your result.

Source files for this tutorial

PDF file

A pdf version of this document is available.