The aim of this tutorial is to demonstrate the solution of the axisymmetric equations of linear elasticity in cylindrical polar coordinates.

Acknowledgement:

This implementation of the equations and the documentation were developed jointly with Matthew Russell with financial support to Chris Bertram from the Chiari and Syringomyelia Foundation.

Theory

Consider a three-dimensional, axisymmetric body (of density $\rho$ , Young's modulus , and Poisson's ratio $\nu$ ), occupying the region whose boundary is $\partial D$ . Using cylindrical coordinates $(r^*,\theta,z^*)$ , the equations of linear elasticity can be written as

$\nabla^* \cdot \bm{\tau}^* + \rho \mathbf{F}^* = \rho\frac{\partial^2\mathbf{u}^*} {\partial {t^*}^2},$

where $\nabla^* = \left(\frac{\partial}{\partial r^*}, \frac{1}{r^*}\frac{\partial} {\partial \theta},\frac{\partial}{\partial z^*}\right)$ , $\bm{\tau}^*(r^*,z^*,t^*)$ is the stress tensor, $\mathbf{F}^*(r^*,z^*,t^*)$ is the body force and $\mathbf{u^*}(r^*,z^*,t^*)$ is the displacement field.

Note that, despite the fact that none of the above physical quantities depend on the azimuthal angle $\theta$ , each can have a non-zero $\theta$ component. Also note that variables written with a superscript asterisk are dimensional, and their non-dimensional counterparts will be written without an asterisk. (The coordinate $\theta$ is, by definition, non-dimensional, so it will always be written without an asterisk.)

A boundary traction $\hat{\bm{\tau}}^*$ and boundary displacement $\hat{\mathbf{u}}^*$ are imposed along the boundaries $\partial D_\mathrm{n}$ and $\partial D_\mathrm{d}$ respectively, where $\partial D = \partial D_\mathrm{d} \cup \partial D_\mathrm{n}$ so that

$\mathbf{u}^* = \hat{\mathbf{u}}^*\text{ on }\partial D_\mathrm{d}, \qquad \bm{\tau}^*\cdot\mathbf{n} = \hat{\bm{\tau}}^*\text{ on }\partial D_\mathrm{n},$

where $\mathbf{n}$ is the outer unit normal vector.

The constitutive equations relating the stresses to the displacements are

$\bm{\tau}^* = \frac{E}{1+\nu}\left(\frac{\nu}{1-2\nu}\left(\nabla^*\cdot\mathbf{u}^*\right) \mathbf{I} + \frac{1}{2}\left(\nabla^*\mathbf{u}^* + \left(\nabla^*\mathbf{u}^*\right)^\mathrm{T}\right)\right),$

where $\mathbf{I}$ is the identity tensor and superscript $\mathrm{T}$ denotes the transpose. In cylindrical coordinates, the matrix representation of the tensor $\nabla^*\mathbf{u}^*$ is

$\nabla^*\mathbf{u}^* = \begin{pmatrix} \dfrac{\strut \partial u_r^*}{\strut \partial r^*} & -\dfrac{\strut u_\theta^*}{\strut r^*} & \dfrac{\strut \partial u_r^*}{\strut \partial z^*}\\ \dfrac{\strut \partial u_\theta^*}{\strut \partial r^*} & \dfrac{\strut u_r^*}{\strut r^*} & \dfrac{\strut \partial u_\theta^*}{\strut \partial z^*}\\ \dfrac{\strut \partial u_z^*}{\strut \partial r^*} & 0 & \dfrac{\strut \partial u_z^*}{\strut \partial z^*} \end{pmatrix}$

and $\nabla^*\cdot \mathbf{u}^*$ is equal to the trace of this matrix.

We non-dimensionalise the equations, using a problem specific reference length, $\mathcal{L}$ , and a timescale $\mathcal{T}$ , and use Young's modulus to non-dimensionalise the body force and the stress tensor:

$\bm{\tau}^* = E \bm{\tau}, \qquad r^* = \mathcal{L}r, \qquad z^* = \mathcal{L}z$

$\mathbf{u}^* = \mathcal{L} \mathbf{u} \qquad \mathbf{F}^* = \frac{E}{\rho \mathcal{L}}\mathbf{F}, \qquad t^* = \mathcal{T}t.$

The non-dimensional form of the axisymmetric linear elasticity equations is then given by

$\nabla\cdot \bm{\tau} + \mathbf{F} = \Lambda^2\frac{\partial^2\mathbf{u}} {\partial t^2},\qquad\qquad (1)$

where $\nabla = \left(\frac{\partial}{\partial r}, \frac{1}{r}\frac{\partial} {\partial \theta},\frac{\partial}{\partial z}\right)$ ,

$\bm{\tau} = \frac{1}{1+\nu}\left(\frac{\nu}{1-2\nu}\left(\nabla\cdot\mathbf{u}\right) \mathbf{I} + \frac{1}{2}\left(\nabla\mathbf{u} + \left(\nabla\mathbf{u}\right)^\mathrm{T}\right)\right),\qquad\qquad (2)$

and the non-dimensional parameter

$\Lambda = \frac{\mathcal{L}}{\mathcal{T}}\sqrt{\frac{\rho}{E}}$

is the ratio of the elastic body's intrinsic timescale, $\mathcal{L} \sqrt{\frac{\rho}{E}}$ , to the problem-specific timescale, $\mathcal{T}$ , that we use for time-dependent problems. The boundary conditions are

$\mathbf{u} = \hat{\mathbf{u}}\text{ on } \partial D_\mathrm{d}\qquad \bm{\tau}\cdot\mathbf{n} = \hat{\bm{\tau}}\text{ on } \partial D_\mathrm{n}.$

We must also specify initial conditions:

$\left.\mathbf{u}\right|_{t=t_0} = \mathbf{u}^0,\qquad \left.\frac{\partial\mathbf{u}}{\partial t}\right|_{t=t_0} = \mathbf{v}^0.\qquad\qquad (3)$

Implementation

Within oomph-lib, the non-dimensional version of the axisymmetric linear elasticity equations (1) combined with the constitutive equations (2) are implemented in the AxisymmetricLinearElasticityEquations class. This class implements the equations in a way which is general with respect to the specific element geometry. To obtain a fully functioning element class, we must combine the equations class with a specific geometric element class, as discussed in the (Not-So-)Quick Guide. For example, we will combine the AxisymmetricLinearElasticityEquations class with QElement<2,3> elements, which are 9-node quadrilateral elements, in our example problem. As usual, the mapping between local and global (Eulerian) coordinates within an element is given by

$x_i = \sum_{j=1}^{N^{(E)}} X_{ij}^{(E)}\psi_j,\qquad i = 1,2,$

where ; $N^{(E)}$ is the number of nodes in the element. $X_{ij}^{(E)}$ is the -th global (Eulerian) coordinate of the -th node in the element and the $\psi_j$ are the element's shape functions, which are specific to each type of geometric element.

We store the three components of the displacement vector as nodal data in the order $u_r, u_z, u_\theta$ and use the shape functions to interpolate the displacements as

$u_i = \sum_{j=1}^{N^{(E)}}U_{ij}^{(E)}\psi_{ij},\qquad i = 1,\dotsc,3,$

where $U_{ij}$ is the -th displacement component at the -th node in the element, i.e., $u_1=u_r, u_2=u_z,u_3=u_\theta$ .

The solution of time dependent problems requires the specification of a TimeStepper that is capable of approximating second time derivatives. In the example problem below we use the Newmark timestepper.

The test problem

As a test problem we consider forced oscillations of the circular cylinder shown in the sketch below:

Azimuthal cross-section of the geometry.

It is difficult to find non-trivial exact solutions of the governing equations (1), (2), so we manufacture a time-harmonic solution:

$\mathbf{u} = \begin{pmatrix} u_r\\ u_\theta\\ u_z \end{pmatrix} = \cos(t) \begin{pmatrix} r^3\cos(z)\\ r^3z^3\\ r^3\sin(z) \end{pmatrix}.\qquad\qquad (4)$

This is an exact solution if we set the body force to

$\mathbf{F} = \cos(t) \begin{pmatrix} -r\cos(z)\left\{\left(8+3r\right)\lambda + \left(16 - r\left(r-3\right)\right)\mu + r^2\Lambda^2\right\}\\ -r\left\{8z^3\mu + r^2\left(z^3\Lambda^2 + 6\mu z\right)\right\}\\ r\sin(z)\left\{- 9\mu + 4r\left(\lambda + \mu\right) + r^2\left(\lambda + 2\mu - \Lambda^2\right)\right\} \end{pmatrix},\qquad\qquad (5)$

where $\lambda = \nu/((1+\nu)(1-2\nu))$ and $\mu = 1/(2(1+\nu))$ are the nondimensional Lamé parameters. We impose the displacement along the boundaries $r=r_\mathrm{max}, z=z_\mathrm{min}, z=z_\mathrm{max}$ according to (4), and impose the traction

$\hat{\bm{\tau}}_3 = \bm{\tau}(r_\mathrm{min},z,t) = \cos(\omega t) \begin{pmatrix} -\cos(z)r_\mathrm{min}^2\left(6\mu + \lambda\left(4+r_\mathrm{min}\right)\right)\\ -2\mu r_\mathrm{min}^2z^3\\ -\mu r_\mathrm{min}^2\sin(z)\left(3-r_\mathrm{min}\right) \end{pmatrix},\qquad\qquad (6)$

along the boundary $r = r_\mathrm{min}$ .

The problem we are solving then consists of equations (1), (2) along with the body force, (5) and boundary traction (6). The initial conditions for the problem are the exact displacement, velocity (and acceleration; see below) according to the solution (4).

Results

The animation below shows the time dependent deformation of the cylinder in the - plane, while the colour contours indicate the azimuthal displacement component. The animation is for $t \in [0,2\pi]$ , since the time scale is nondimensionalised on the reciprocal of the angular frequency of the oscillations.

Animation (HTML only) of the resulting displacement field.

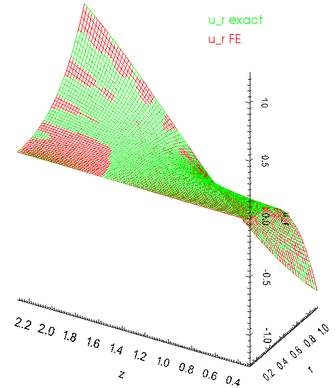
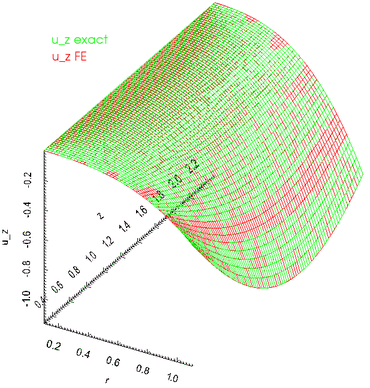
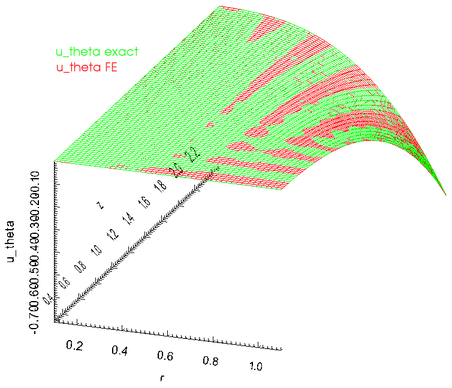
The next three figures show plots of the radial, axial and azimuthal displacements as functions of at . Note the excellent agreement between the numerical and exact solutions.

Comparison between exact and FE solutions for the r-component of displacement at t = 2.64

Comparison between exact and FE solutions for the z-component of displacement at t = 2.64

Comparison between exact and FE solutions for the theta-component of displacement at t = 2.64

Global parameters and functions

As usual, we define all non-dimensional parameters in a namespace. In this namespace, we also define the body force, the traction to be applied on the boundary $r=r_\mathrm{min}$ , and the exact solution. Note that, consistent with the enumeration of the unknowns, discussed above, the order of the components in the functions that specify the body force and the surface traction is $(r,z,\theta)$ .

//===start_of_Global_Parameters_namespace===============================
/// Namespace for global parameters
//======================================================================
namespace Global_Parameters
{
 /// Define Poisson's ratio Nu
 double Nu = 0.3;
 
 /// Define the non-dimensional Young's modulus
 double E = 1.0;
 
 /// Lame parameters
 double Lambda = E*Nu/(1.0+Nu)/(1.0-2.0*Nu);
 double Mu = E/2.0/(1.0+Nu);
 
 /// Square of the frequency of the time dependence
 double Omega_sq = 0.5;
 
 /// Number of elements in r-direction
 unsigned Nr = 5;
 
 /// Number of elements in z-direction
 unsigned Nz = 10;
 
 /// Length of domain in r direction
 double Lr = 1.0;
 
 /// Length of domain in z-direction
 double Lz = 2.0;
 
 /// Set up min r coordinate
 double Rmin = 0.1;
 
 /// Set up min z coordinate
 double Zmin = 0.3;
 
 /// Set up max r coordinate
 double Rmax = Rmin+Lr;
 
 /// Set up max z coordinate
 double Zmax = Zmin+Lz;
 
 /// The traction function at r=Rmin: (t_r, t_z, t_theta)
 void boundary_traction(const double &time,
                        const Vector<double> &x,
                        const Vector<double> &n,
                        Vector<double> &result)
 {
  result[0] = cos(time)*(-6.0*pow(x[0],2)*Mu*cos(x[1])-
   Lambda*(4.0*pow(x[0],2)+pow(x[0],3))*cos(x[1]));
  result[1] = cos(time)*(-Mu*(3.0*pow(x[0],2)-pow(x[0],3))*sin(x[1]));
  result[2] = cos(time)*(-Mu*pow(x[0],2)*(2*pow(x[1],3)));
 }
 
 /// The body force function; returns vector of doubles
 /// in the order (b_r, b_z, b_theta)
 void body_force(const double &time,
                 const Vector<double> &x,
                 Vector<double> &result)
 {
  result[0] = cos(time)*(
   x[0]*(-cos(x[1])*
         (Lambda*(8.0+3.0*x[0])-
          Mu*(-16.0+x[0]*(x[0]-3.0))+pow(x[0],2)*Omega_sq)));
  result[1] = cos(time)*(
   x[0]*sin(x[1])*(Mu*(-9.0)+
                   4.0*x[0]*(Lambda+Mu)+pow(x[0],2)*
                   (Lambda+2.0*Mu-Omega_sq)));
  result[2] = cos(time)*(
   -x[0]*(8.0*Mu*pow(x[1],3)+pow(x[0],2)*(pow(x[1],3)*Omega_sq+6.0*Mu*x[1])));
 } // end of body force

In addition, the namespace includes the necessary machinery for providing the time dependent equations with their initial data from the exact solution. There are 9 functions, one for each of the components of displacement, velocity and acceleration, and a helper function. For brevity, we list only one of these functions; the others are similar.

 /// Calculate the time dependent form of the r-component of displacement
 double u_r(const double &time, const Vector<double> &x)
  {
   Vector<double> displ(3);
   exact_solution_th(x,displ);
   return cos(time)*displ[0];
  } // end_of_u_r

The driver code

We start by creating a DocInfo object that will be used to output the solution, and then build the problem.

//===start_of_main======================================================
/// Driver code 
//======================================================================
int main(int argc, char* argv[])
{
 // Store command line arguments
 CommandLineArgs::setup(argc,argv);
 
 // Define possible command line arguments and parse the ones that
 // were actually specified
 
 // Validation?
 CommandLineArgs::specify_command_line_flag("--validation");
 
 // Parse command line
 CommandLineArgs::parse_and_assign(); 
 
 // Doc what has actually been specified on the command line
 CommandLineArgs::doc_specified_flags();
 
 // Set up doc info
 DocInfo doc_info;
 
 // Set output directory
 doc_info.set_directory("RESLT");
 
 // Time dependent problem instance
 AxisymmetricLinearElasticityProblem
  <QAxisymmetricLinearElasticityElement<3>, Newmark<1> > problem;

Next we set up a timestepper and assign the initial conditions.

 // Set the initial time to t=0
 problem.time_pt()->time()=0.0;
 
 // Set and initialise timestep
 double dt=0;
 
 // If we're validating, use a larger timestep so that we can do fewer steps
 // before reaching interesting behaviour
 if(CommandLineArgs::command_line_flag_has_been_set("--validation"))
  {
   dt=0.1;
  }
 else // Otherwise use a small timestep
  {
   dt=0.01;
  }
 problem.time_pt()->initialise_dt(dt);
 
 // Set the initial conditions
 problem.set_initial_conditions();
 
 // Doc the initial conditions and increment the doc_info number
 problem.doc_solution(doc_info);
 doc_info.number()++;

We calculate the number of timesteps to perform - if we are validating, just do small number of timesteps; otherwise do a full period the time-harmonic oscillation.

 // Find the number of timesteps to perform
 unsigned nstep=0;
 
 // If we're validating, only do a few timesteps; otherwise do a whole period
 if(CommandLineArgs::command_line_flag_has_been_set("--validation"))
  {
   nstep=5;
  }
 else // Otherwise calculate based on timestep
  {
   // Solve for one full period
   double t_max=2*MathematicalConstants::Pi;
 
   nstep=unsigned(t_max/dt);
  } //end_of_calculate_number_of_timesteps

Finally we perform a time dependent simulation.

 // Do the timestepping
 for(unsigned istep=0;istep<nstep;istep++)
  {
   // Solve for this timestep
   problem.unsteady_newton_solve(dt);
 
   // Doc the solution and increment doc_info number
   problem.doc_solution(doc_info);
   doc_info.number()++;
  }
} // end_of_main

The problem class

The problem class is very simple, and similarly to other problems with Neumann conditions, there are separate meshes for the "bulk" elements and the "face" elements that apply the traction boundary conditions. The function assign_traction_elements() attaches the traction elements to the appropriate bulk elements.

//===start_of_problem_class=============================================
/// Class to validate time harmonic linear elasticity (Fourier 
/// decomposed)
//======================================================================
template<class ELEMENT, class TIMESTEPPER>
class AxisymmetricLinearElasticityProblem : public Problem
{
public:
 
 /// Constructor: Pass number of elements in r and z directions,
 /// boundary locations and whether we are doing an impulsive start or not
 AxisymmetricLinearElasticityProblem();
 
 /// Update before solve is empty
 void actions_before_newton_solve() {}
 
 /// Update after solve is empty
 void actions_after_newton_solve() {}
 
 /// Actions before implicit timestep
 void actions_before_implicit_timestep()
  {
   // Just need to update the boundary conditions
   set_boundary_conditions();
  }
 
 /// Set the initial conditions, either for an impulsive start or
 /// with history values for the time stepper
 void set_initial_conditions();
 
 /// Set the boundary conditions
 void set_boundary_conditions();
 
 /// Doc the solution
 void doc_solution(DocInfo& doc_info);
 
private:
 
 /// Allocate traction elements on the bottom surface
 void assign_traction_elements();
 
 /// Pointer to the bulk mesh
 Mesh* Bulk_mesh_pt;
 
 /// Pointer to the mesh of traction elements
 Mesh* Surface_mesh_pt;
}; // end_of_problem_class

The problem constructor

The problem constructor creates the mesh objects (which in turn create the elements), pins the appropriate boundary nodes and assigns the boundary conditions according to the functions defined in the Global_Parameters namespace.

//===start_of_constructor=============================================
/// Problem constructor: Pass number of elements in coordinate
/// directions and size of domain.
//====================================================================
template<class ELEMENT, class TIMESTEPPER>
AxisymmetricLinearElasticityProblem<ELEMENT, TIMESTEPPER>::
AxisymmetricLinearElasticityProblem()
{
 //Allocate the timestepper
 add_time_stepper_pt(new TIMESTEPPER());
 
 //Now create the mesh
 Bulk_mesh_pt = new RectangularQuadMesh<ELEMENT>(
   Global_Parameters::Nr,
   Global_Parameters::Nz,
   Global_Parameters::Rmin,
   Global_Parameters::Rmax,
   Global_Parameters::Zmin,
   Global_Parameters::Zmax,
   time_stepper_pt());
 
 //Create the surface mesh of traction elements
 Surface_mesh_pt=new Mesh;
 assign_traction_elements();
 
 //Set the boundary conditions
 set_boundary_conditions();

Then the physical parameters are set for each element in the bulk mesh.

 
 // Complete the problem setup to make the elements fully functional
 
 // Loop over the elements
 unsigned n_el = Bulk_mesh_pt->nelement();
 for(unsigned e=0;e<n_el;e++)
  {
   // Cast to a bulk element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(Bulk_mesh_pt->element_pt(e));
 
   // Set the body force
   el_pt->body_force_fct_pt() = &Global_Parameters::body_force;
 
   // Set the pointer to Poisson's ratio
   el_pt->nu_pt() = &Global_Parameters::Nu;
 
   // Set the pointer to non-dim Young's modulus
   el_pt->youngs_modulus_pt() = &Global_Parameters::E;
 
   // Set the pointer to the Lambda parameter
   el_pt->lambda_sq_pt() = &Global_Parameters::Omega_sq;
 
  }// end_loop_over_elements

We then loop over the traction elements and set the applied traction.

 
 // Loop over the traction elements
 unsigned n_traction =  Surface_mesh_pt->nelement();
 for(unsigned e=0;e<n_traction;e++)
  {
   // Cast to a surface element
   AxisymmetricLinearElasticityTractionElement<ELEMENT>*
    el_pt = 
    dynamic_cast<AxisymmetricLinearElasticityTractionElement
    <ELEMENT>* >(Surface_mesh_pt->element_pt(e));
   
   // Set the applied traction
   el_pt->traction_fct_pt() = &Global_Parameters::boundary_traction;
   
  }// end_loop_over_traction_elements

Finally, we add the two meshes as sub-meshes, build a global mesh from these and assign the equation numbers.

 // Add the submeshes to the problem
 add_sub_mesh(Bulk_mesh_pt);
 add_sub_mesh(Surface_mesh_pt);
 
 // Now build the global mesh
 build_global_mesh();
 
 // Assign equation numbers
 cout << assign_eqn_numbers() << " equations assigned" << std::endl; 
} // end_of_constructor

The traction elements

We create the face elements that apply the traction to the boundary $r=r_\mathrm{min}$ .

//===start_of_traction===============================================
/// Make traction elements along the boundary r=Rmin
//===================================================================
template<class ELEMENT, class TIMESTEPPER>
void AxisymmetricLinearElasticityProblem<ELEMENT, TIMESTEPPER>::
assign_traction_elements()
{
 unsigned bound, n_neigh;
 
 // How many bulk elements are next to boundary 3
 bound=3;
 n_neigh = Bulk_mesh_pt->nboundary_element(bound); 
 
 // Now loop over bulk elements and create the face elements
 for(unsigned n=0;n<n_neigh;n++)
  {
   // Create the face element
   FiniteElement *traction_element_pt 
    = new AxisymmetricLinearElasticityTractionElement<ELEMENT>
    (Bulk_mesh_pt->boundary_element_pt(bound,n),
     Bulk_mesh_pt->face_index_at_boundary(bound,n));
 
   // Add to mesh
   Surface_mesh_pt->add_element_pt(traction_element_pt);
  }
 
} // end of assign_traction_elements

Initial data

The time integration in this problem is performed using the Newmark scheme which, in addition to the standard initial conditions (3), requires an initial value for the acceleration. Since we will be solving a test case in which the exact solution is known, we can use the exact solution to provide the complete set of initial data required. For the details of the Newmark scheme, see the tutorial on the linear wave equation.

If we're doing an impulsive start, set the displacement, velocity and acceleration to zero, and fill in the time history to be consistent with this.

//===start_of_set_initial_conditions=================================
/// Set the initial conditions (history values)
//===================================================================
template<class ELEMENT, class TIMESTEPPER>
void AxisymmetricLinearElasticityProblem<ELEMENT, TIMESTEPPER>::
set_initial_conditions()
{
 // Upcast the timestepper to the specific type we have
 TIMESTEPPER* timestepper_pt =
  dynamic_cast<TIMESTEPPER*>(time_stepper_pt());
 
 // By default do a non-impulsive start and provide initial conditions
 bool impulsive_start=false;
 
 if(impulsive_start)
  {
   // Number of nodes in the bulk mesh
   unsigned n_node = Bulk_mesh_pt->nnode();
 
   // Loop over all nodes in the bulk mesh
   for(unsigned inod=0;inod<n_node;inod++)
    {
     // Pointer to node
     Node* nod_pt = Bulk_mesh_pt->node_pt(inod);
 
     // Get nodal coordinates
     Vector<double> x(2);
     x[0] = nod_pt->x(0);
     x[1] = nod_pt->x(1);
 
     // Assign zero solution at t=0
     nod_pt->set_value(0,0);
     nod_pt->set_value(1,0);
     nod_pt->set_value(2,0);
 
     // Set the impulsive initial values in the timestepper
     timestepper_pt->assign_initial_values_impulsive(nod_pt);
    }
  } // end_of_impulsive_start

If we are not doing an impulsive start, we must provide the timestepper with time history values for the displacement, velocity and acceleration. Each component of the these vectors is represented by a function pointer, and in this case, the function pointers return values based on the exact solution.

 else // Smooth start
  {
   // Storage for pointers to the functions defining the displacement,
   // velocity and acceleration components
   Vector<typename TIMESTEPPER::NodeInitialConditionFctPt>
    initial_value_fct(3);
   Vector<typename TIMESTEPPER::NodeInitialConditionFctPt>
    initial_veloc_fct(3);
   Vector<typename TIMESTEPPER::NodeInitialConditionFctPt>
    initial_accel_fct(3);
 
   // Set the displacement function pointers
   initial_value_fct[0]=&Global_Parameters::u_r;
   initial_value_fct[1]=&Global_Parameters::u_z;
   initial_value_fct[2]=&Global_Parameters::u_theta;
 
   // Set the velocity function pointers
   initial_veloc_fct[0]=&Global_Parameters::d_u_r_dt;
   initial_veloc_fct[1]=&Global_Parameters::d_u_z_dt;
   initial_veloc_fct[2]=&Global_Parameters::d_u_theta_dt;
 
   // Set the acceleration function pointers
   initial_accel_fct[0]=&Global_Parameters::d2_u_r_dt2;
   initial_accel_fct[1]=&Global_Parameters::d2_u_z_dt2;
   initial_accel_fct[2]=&Global_Parameters::d2_u_theta_dt2;

Then we loop over all nodes in the bulk mesh and set the initial data values from the exact solution.

   // Number of nodes in the bulk mesh
   unsigned n_node = Bulk_mesh_pt->nnode();
 
   // Loop over all nodes in bulk mesh
   for(unsigned inod=0;inod<n_node;inod++)
    {
     // Pointer to node
     Node* nod_pt = Bulk_mesh_pt->node_pt(inod);
 
     // Assign the history values
     timestepper_pt->assign_initial_data_values(nod_pt,
                                                initial_value_fct,
                                                initial_veloc_fct,
                                                initial_accel_fct);
    } // end_of_loop_over_nodes

Post-processing

This member function documents the computed solution to file and calculates the error between the computed solution and the exact solution.

//==start_of_doc_solution=================================================
/// Doc the solution
//========================================================================
template<class ELEMENT, class TIMESTEPPER>
void AxisymmetricLinearElasticityProblem<ELEMENT, TIMESTEPPER>::
doc_solution(DocInfo& doc_info)
{ 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned npts=10; 
 
 // Output solution 
 sprintf(filename,"%s/soln%i.dat",doc_info.directory().c_str(),
   doc_info.number());
 some_file.open(filename);
 Bulk_mesh_pt->output(some_file,npts);
 some_file.close();
 
 // Output exact solution 
 sprintf(filename,"%s/exact_soln%i.dat",doc_info.directory().c_str(),
   doc_info.number());
 some_file.open(filename);
 Bulk_mesh_pt->output_fct(some_file,npts,time_pt()->time(),
                          Global_Parameters::exact_solution);
 some_file.close();
 
 // Doc error
 double error=0.0;
 double norm=0.0;
 sprintf(filename,"%s/error%i.dat",doc_info.directory().c_str(),
   doc_info.number());
 some_file.open(filename);
 Bulk_mesh_pt->compute_error(some_file,
                             Global_Parameters::exact_solution, 
                             time_pt()->time(),
                             error,norm);
 some_file.close();
 
 // Doc error norm:
 cout << "\nNorm of error:    " << sqrt(error) << std::endl; 
 cout << "Norm of solution: " << sqrt(norm) << std::endl << std::endl;
 cout << std::endl;
} // end_of_doc_solution   

Comments

Given that we non-dimensionalised all stresses on Young's modulus it seems odd that we provide the option to specify a non-dimensional Young's modulus via the member function AxisymmetricLinearElasticity::youngs_modulus_pt(). The explanation for this is that this function specifies the ratio of the material's actual Young's modulus to the Young's modulus used in the non-dimensionalisation of the equations. The capability to specify such ratios is important in problems where the elastic body is made of multiple materials with different constitutive properties. If the body is made of a single, homogeneous material, the specification of the non-dimensional Young's modulus is not required – it defaults to 1.0.

Exercises

Try setting the boolean flag impulsive_start to true in the AxisymmetricLinearElasticityProblem::set_initial_conditions function and compare the system's evolution to that obtained when a "smooth" start from the exact solution is performed.
Omit the specification of the Young's modulus and verify that the default value gives the same solution.
Confirm that the assignment of the history values for the Newmark timestepper in AxisymmetricLinearElasticityProblem::set_initial_conditions sets the correct initial values for the displacement, velocity and acceleration. (Hint: the relevant code is already contained in the driver code, but was omitted in the code listings shown above.)

Source files for this tutorial

The source files for this tutorial are located in the directory:

demo_drivers/axisym_linear_elasticity/cylinder/
The driver code is:

demo_drivers/axisym_linear_elasticity/cylinder/cylinder.cc

PDF file

A pdf version of this document is available.