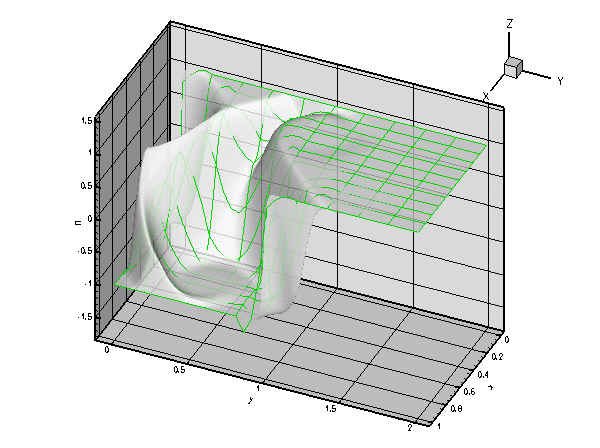
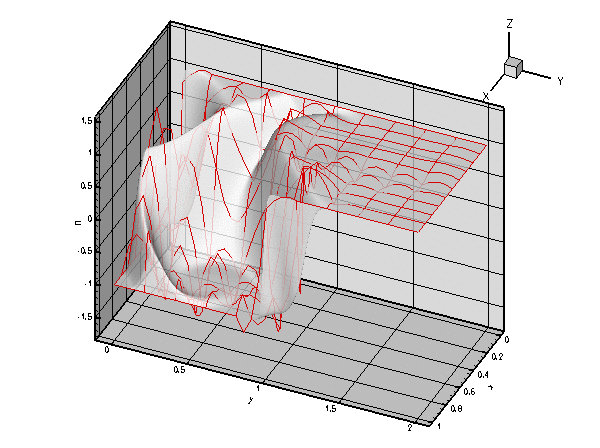
In this example we discuss the SUPG-stabilised solution of the 2D advection-diffusion problem

Two-dimensional advection-diffusion problem in a rectangular domain

Solve

$\mbox{Pe}\ \sum_{i=1}^2 w_i \left(x_1,x_2\right) \frac{\partial u}{\partial x_i} = \sum_{i=1}^2 \frac{\partial^2u}{\partial x_i^2} + f(x_1,x_2), \ \ \ \ \ \ \ \ \ \ (1)$

in the rectangular domain $D =\left\{ (x_1,x_2) \in [0,1] \times [0,2]\right\}$ , with Dirichlet boundary conditions

$\left. u\right|_{\partial D}=u_0, \ \ \ \ \ \ \ \ \ \ (2)$

where the Peclet number, $\mbox{Pe}$ the boundary values, , the source function
and the components of the "wind" $w_i(x_1,x_2) \ (i=1,2)$ are given.

We set and assign the boundary conditions such that

$u_0(x_1,x_2) = \tanh(1-\alpha(x_1 \tan\Phi - x_2)), \ \ \ \ \ \ \ \ \ (3)$

For large values of $\alpha,$ this boundary data approaches a step, oriented at an angle $\Phi$ against the axis.

In the computations we will impose the "wind"

$\mathbf{w}\left(x_1,x_2 \right) = \left( \begin{array}{c} \sin(6x_2) \\ \cos(6x_1) \end{array} \right), \ \ \ \ \ \ \ \ \ (4)$

illustrated in this vector plot:

Plot of the wind.

The figures below show plots of the solution for $\Phi=45^\circ, \ \alpha=50$ and a Peclet number of , with and without SUPG stabilisation. The wire-mesh plot shows the solution computed on a 10x10 mesh, the shaded surface represents the solution obtained from an unstabilised solution on a 150x150 mesh. Note how SUPG stabilisation "suppresses the wiggles" on the relatively coarse mesh.

Plot of the SUPG-stabilised solution at different levels of mesh refinement.

Plot of the unstabilised solution at different levels of mesh refinement.

The driver code

Overall, the structure of the driver code is very similar to that used for the problem without stabilisation.

To be written:

Discuss SUPG theory.
Implementation and the role of basis, shape and test functions (our equations are isoparametric)

Until we get around to completing this example, here's the driver code. Fairly self-explanatory, isn't it?

//LIC// ====================================================================
//LIC// This file forms part of oomph-lib, the object-oriented, 
//LIC// multi-physics finite-element library, available 
//LIC// at http://www.oomph-lib.org.
//LIC// 
//LIC// Copyright (C) 2006-2023 Matthias Heil and Andrew Hazel
//LIC// 
//LIC// This library is free software; you can redistribute it and/or
//LIC// modify it under the terms of the GNU Lesser General Public
//LIC// License as published by the Free Software Foundation; either
//LIC// version 2.1 of the License, or (at your option) any later version.
//LIC// 
//LIC// This library is distributed in the hope that it will be useful,
//LIC// but WITHOUT ANY WARRANTY; without even the implied warranty of
//LIC// MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the GNU
//LIC// Lesser General Public License for more details.
//LIC// 
//LIC// You should have received a copy of the GNU Lesser General Public
//LIC// License along with this library; if not, write to the Free Software
//LIC// Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA
//LIC// 02110-1301  USA.
//LIC// 
//LIC// The authors may be contacted at oomph-lib@maths.man.ac.uk.
//LIC// 
//LIC//====================================================================
//Driver for a simple 2D adv diff problem with SUPG stabilisation
 
//Generic routines
#include "generic.h"
 
// The Poisson equations
#include "advection_diffusion.h"
 
// The mesh 
#include "meshes/rectangular_quadmesh.h"
 
using namespace std;
 
using namespace oomph;
 
 
 
//======start_of_namespace============================================
/// Namespace for global parameters: Unforced problem with
/// boundary values corresponding to a steep tanh step profile
/// oriented at 45 degrees across the domain.
//====================================================================
namespace GlobalPhysicalParameters
{
 
 /// Peclet number
 double Peclet=200.0;
 
 /// Parameter for steepness of step in boundary values
 double Alpha=50.0;
 
 /// Parameter for angle of step in boundary values: 45 degrees
 double TanPhi=1.0;
 
 /// Some "solution" for assignment of boundary values
 void get_boundary_values(const Vector<double>& x, Vector<double>& u)
 {
  u[0]=tanh(1.0-Alpha*(TanPhi*x[0]-x[1]));
 }
 
 /// Zero source function
 void source_function(const Vector<double>& x_vect, double& source)
 {
  source=0.0;
 }
 
 /// Wind
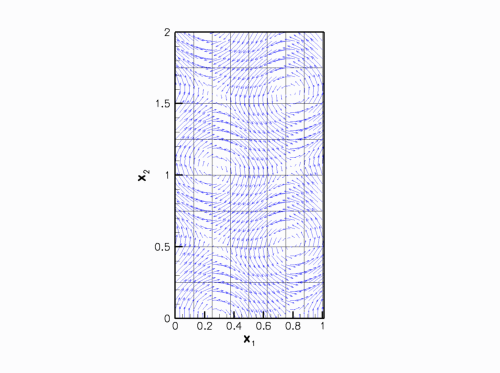
 void wind_function(const Vector<double>& x, Vector<double>& wind)
 {
  wind[0]=sin(6.0*x[1]);
  wind[1]=cos(6.0*x[0]);
 }
 
 
} // end of namespace
 
/// ///////////////////////////////////////////////////////////////////
/// ///////////////////////////////////////////////////////////////////
/// ///////////////////////////////////////////////////////////////////
 
 
//====== start_of_problem_class=======================================
/// 2D AdvectionDiffusion problem on rectangular domain, discretised 
/// with refineable 2D QAdvectionDiffusion elements. The specific type
/// of element is specified via the template parameter.
//====================================================================
template<class ELEMENT> 
class SUPGAdvectionDiffusionProblem : public Problem
{
 
public:
 
 /// Constructor: Pass pointer to source and wind functions, and
 /// flag to indicate if stabilisation is to be used.
 SUPGAdvectionDiffusionProblem(
  AdvectionDiffusionEquations<2>::AdvectionDiffusionSourceFctPt source_fct_pt,
  AdvectionDiffusionEquations<2>::AdvectionDiffusionWindFctPt wind_fct_pt,
  const bool& use_stabilisation);
 
 /// Destructor. Empty
 ~SUPGAdvectionDiffusionProblem(){}
 
 /// Update the problem specs before solve: Reset boundary conditions
 /// to the values from the tanh solution and compute stabilisation
 /// parameter.
 void actions_before_newton_solve();
 
 /// Update the problem after solve (empty)
 void actions_after_newton_solve(){}
 
 /// Doc the solution.
 void doc_solution();
 
 /// Overloaded version of the problem's access function to 
 /// the mesh. Recasts the pointer to the base Mesh object to 
 /// the actual mesh type.
 RectangularQuadMesh<ELEMENT>* mesh_pt() 
  {
   return dynamic_cast<RectangularQuadMesh<ELEMENT>*>(
    Problem::mesh_pt());
  }
 
private:
 
 /// DocInfo object
 DocInfo Doc_info;
 
 /// Pointer to source function
 AdvectionDiffusionEquations<2>::AdvectionDiffusionSourceFctPt Source_fct_pt;
 
 /// Pointer to wind function
 AdvectionDiffusionEquations<2>::AdvectionDiffusionWindFctPt Wind_fct_pt;
 
 /// Flag to indicate if stabilisation is to be used
 bool Use_stabilisation;
 
}; // end of problem class
 
 
 
//=====start_of_constructor===============================================
/// Constructor for AdvectionDiffusion problem: Pass pointer to 
/// source function and wind functions and flag to indicate 
/// if stabilisation is to be used.
//========================================================================
template<class ELEMENT>
SUPGAdvectionDiffusionProblem<ELEMENT>::SUPGAdvectionDiffusionProblem(
 AdvectionDiffusionEquations<2>::AdvectionDiffusionSourceFctPt source_fct_pt,
 AdvectionDiffusionEquations<2>::AdvectionDiffusionWindFctPt wind_fct_pt,
 const bool& use_stabilisation)
 :  Source_fct_pt(source_fct_pt), Wind_fct_pt(wind_fct_pt), 
    Use_stabilisation(use_stabilisation)
{ 
 
 // Set output directory
 if (use_stabilisation)
  {
   Doc_info.set_directory("RESLT_stabilised");
  }
 else
  {
   Doc_info.set_directory("RESLT_unstabilised");
  }
 
 // Setup mesh
 
 // # of elements in x-direction
 unsigned n_x=40;
 
 // # of elements in y-direction
 unsigned n_y=40;
 
 // Domain length in x-direction
 double l_x=1.0;
 
 // Domain length in y-direction
 double l_y=2.0;
 
 // Build and assign mesh
 Problem::mesh_pt() = 
  new RectangularQuadMesh<ELEMENT>(n_x,n_y,l_x,l_y);
 
  
 // Set the boundary conditions for this problem: All nodes are
 // free by default -- only need to pin the ones that have Dirichlet 
 // conditions here
 unsigned num_bound = mesh_pt()->nboundary();
 for(unsigned ibound=0;ibound<num_bound;ibound++)
  {
   unsigned num_nod= mesh_pt()->nboundary_node(ibound);
   for (unsigned inod=0;inod<num_nod;inod++)
    {
     mesh_pt()->boundary_node_pt(ibound,inod)->pin(0); 
    }
  } // end loop over boundaries
 
 // Complete the build of all elements so they are fully functional 
 
 // Loop over the elements to set up element-specific 
 // things that cannot be handled by the (argument-free!) ELEMENT 
 // constructor: Pass pointer to source function
 unsigned n_element = mesh_pt()->nelement();
 for(unsigned i=0;i<n_element;i++)
  {
   // Upcast from GeneralsedElement to the present element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(i));
 
   //Set the source function pointer
   el_pt->source_fct_pt() = Source_fct_pt;
 
   //Set the wind function pointer
   el_pt->wind_fct_pt() = Wind_fct_pt;
 
   // Set the Peclet number
   el_pt->pe_pt() = &GlobalPhysicalParameters::Peclet;
  }
 
 // Setup equation numbering scheme
 cout <<"Number of equations: " << assign_eqn_numbers() << std::endl; 
 
} // end of constructor
 
 
//========================================start_of_actions_before_newton_solve===
/// Update the problem specs before solve: (Re-)set boundary conditions
//========================================================================
template<class ELEMENT>
void SUPGAdvectionDiffusionProblem<ELEMENT>::actions_before_newton_solve()
{
 // How many boundaries are there?
 unsigned num_bound = mesh_pt()->nboundary();
 
 //Loop over the boundaries
 for(unsigned ibound=0;ibound<num_bound;ibound++)
  {
   // How many nodes are there on this boundary?
   unsigned num_nod=mesh_pt()->nboundary_node(ibound);
 
   // Loop over the nodes on boundary
   for (unsigned inod=0;inod<num_nod;inod++)
    {
     // Get pointer to node
     Node* nod_pt=mesh_pt()->boundary_node_pt(ibound,inod);
 
     // Extract nodal coordinates from node:
     Vector<double> x(2);
     x[0]=nod_pt->x(0);
     x[1]=nod_pt->x(1);
 
     // Get boundary value
     Vector<double> u(1);
     GlobalPhysicalParameters::get_boundary_values(x,u);
 
     // Assign the value to the one (and only) nodal value at this node
     nod_pt->set_value(0,u[0]);
    }
  } 
 
 // Now loop over all elements and set the stabilisation parameter
 unsigned n_element = mesh_pt()->nelement();
 for(unsigned i=0;i<n_element;i++)
  {
   // Upcast from GeneralsedElement to the present element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(i));
   
 
   // Use stabilisation?
   if (Use_stabilisation)
    {
     //Compute stabilisation parameter
     el_pt->compute_stabilisation_parameter();
    }
   else
    {
     //Compute stabilisation parameter
     el_pt->switch_off_stabilisation();
    }
 
  }
 
}  // end of actions before solve
 
 
 
//===============start_of_doc=============================================
/// Doc the solution
//========================================================================
template<class ELEMENT>
void SUPGAdvectionDiffusionProblem<ELEMENT>::doc_solution()
{ 
 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points: npts x npts
 unsigned npts=5;
 
 // Output solution 
 //-----------------
 sprintf(filename,"%s/soln%i.dat",Doc_info.directory().c_str(),
         Doc_info.number());
 some_file.open(filename);
 mesh_pt()->output(some_file,npts);
 some_file.close();
 
} // end of doc
 
 
//===== start_of_main=====================================================
/// Driver code for 2D AdvectionDiffusion problem
//========================================================================
int main()
{
 
 //Set up the problem with stabilisation
 {
  bool use_stabilisation=true;
  
  // Create the problem with 2D nine-node elements from the
  // QAdvectionDiffusionElement family. Pass pointer to 
  // source and wind function. 
  SUPGAdvectionDiffusionProblem<QSUPGAdvectionDiffusionElement<2,3> > 
   problem(&GlobalPhysicalParameters::source_function,
           &GlobalPhysicalParameters::wind_function,
           use_stabilisation);
  
  // Solve the problem
  problem.newton_solve();
  
  //Output the solution
  problem.doc_solution();
  
 }
 
 
 
 //Set up the problem without stabilisation
 {
  
  bool use_stabilisation=false;
  
  // Create the problem with 2D nine-node elements from the
  // QAdvectionDiffusionElement family. Pass pointer to 
  // source and wind function. 
  SUPGAdvectionDiffusionProblem<QSUPGAdvectionDiffusionElement<2,3> > 
   problem(&GlobalPhysicalParameters::source_function,
           &GlobalPhysicalParameters::wind_function,
           use_stabilisation);
  
  // Solve the problem
  problem.newton_solve();
  
  //Output the solution
  problem.doc_solution();
  
 }
 
 
 
} // end of main
 
 
 
 
 
 
 
 
 

Source files for this tutorial

The source files for this tutorial are located in the directory: demo_drivers/advection_diffusion/two_d_adv_diff_SUPG/
The driver code is: demo_drivers/advection_diffusion/two_d_adv_diff_SUPG/two_d_adv_diff_SUPG.cc

PDF file

A pdf version of this document is available.