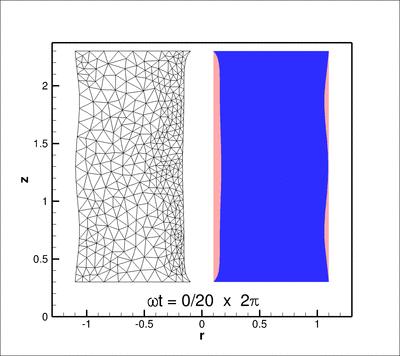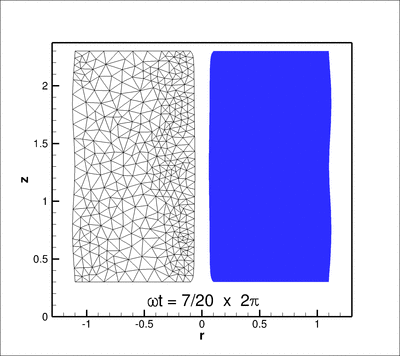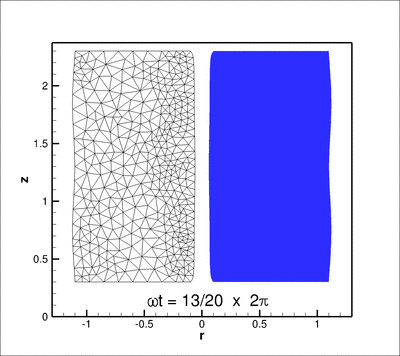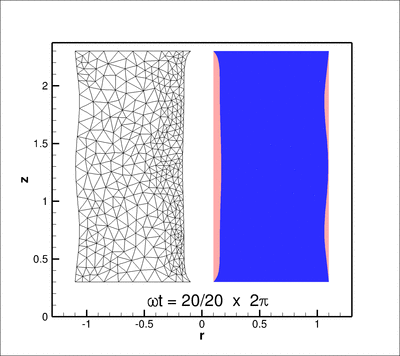
In this tutorial we re-visit the solution of the time-harmonic equations of 3D linear elasticity in cylindrical polar coordinates, using a Fourier decomposition of the solution in the azimuthal direction. The driver code is very similar to the one discussed in another tutorial – the main purpose of the current tutorial is to demonstrate the use of spatial adaptivity on unstructured meshes. Compared to the test case considered in the other tutorial we study a slightly less contrived test problem: the forced time-harmonic oscillations of a finite-length, hollow cylinder, loaded by a time-periodic pressure load on its inner surface.

Acknowledgement: This implementation of the equations and the documentation were developed jointly with Robert Harter (Thales Underwater Systems Ltd) with financial support from a KTA Secondment grant from University of Manchester's EPSRC-funded Knowledge Transfer Account.

The test problem

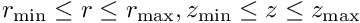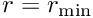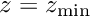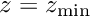The figure below shows the problem considered in this tutorial: an annular elastic body that occupies the region $r_{\rm min}\leq r\leq r_{\rm max}, z_{\rm min}\leq z\leq z_{\rm max}$ is loaded by a time-harmonic pressure load acting on its inner surface (at $r = r_{\rm min}$ ). The upper and lower ends of the hollow cylinder (at $z = z_{\rm min}$ and $z = z_{\rm min}$ ) are held at a fixed position.

Here is an animation of the resulting displacement field for $r_{\rm min} = 0.1$ and $r_{\rm max} = 1.1.$

Forced oscillations of a thick-walled, hollow cylinder, subject to a pressure load on its inner surface. The pink shape in the background shows the cylinder's undeformed shape (in a radial plane); the mesh plotted in the region r < 0 illustrates how spatial adaptivity refines the mesh in regions of sharp displacement gradients (near the loaded surface and the supports).

The numerical solution

The driver code for this problem is very similar to the one discussed in another tutorial. Running sdiff on the two driver codes

demo_drivers/time_harmonic_fourier_decomposed_linear_elasticity/cylinder/cylinder.cc

and

demo_drivers/time_harmonic_fourier_decomposed_linear_elasticity/cylinder/pressure_loaded_cylinder.cc

shows you the differences, the most important of which are:

The change of the forcing to a spatially constant pressure load on the inside boundary.
The provision of the actions_before/after_adapt() functions and a helper function complete_problem_setup() which rebuilds the elements (by passing the problem parameters to the elements) following the unstructured mesh adaptation. (The need/rationale for such a function is discussed in another tutorial.)
The mesh generation and the application of boundary conditions at the upper and lower boundaries of the hollow cylinder. .
All of this is reasonably straightforward and provides a powerful code that automatically adapts the mesh in regions of large displacement gradients. Have a look through the driver code and play with it.

Code listing

Here's a listing of the complete driver code:

//LIC// ====================================================================
//LIC// This file forms part of oomph-lib, the object-oriented, 
//LIC// multi-physics finite-element library, available 
//LIC// at http://www.oomph-lib.org.
//LIC// 
//LIC// Copyright (C) 2006-2024 Matthias Heil and Andrew Hazel
//LIC// 
//LIC// This library is free software; you can redistribute it and/or
//LIC// modify it under the terms of the GNU Lesser General Public
//LIC// License as published by the Free Software Foundation; either
//LIC// version 2.1 of the License, or (at your option) any later version.
//LIC// 
//LIC// This library is distributed in the hope that it will be useful,
//LIC// but WITHOUT ANY WARRANTY; without even the implied warranty of
//LIC// MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the GNU
//LIC// Lesser General Public License for more details.
//LIC// 
//LIC// You should have received a copy of the GNU Lesser General Public
//LIC// License along with this library; if not, write to the Free Software
//LIC// Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA
//LIC// 02110-1301  USA.
//LIC// 
//LIC// The authors may be contacted at oomph-lib@maths.man.ac.uk.
//LIC// 
//LIC//====================================================================
// Driver 
 
// The oomphlib headers
#include "generic.h"
#include "time_harmonic_fourier_decomposed_linear_elasticity.h"
 
// The mesh
#include "meshes/rectangular_quadmesh.h"
#include "meshes/triangle_mesh.h"
 
using namespace std;
 
using namespace oomph;
 
 
//===start_of_namespace=================================================
/// Namespace for global parameters
//======================================================================
namespace Global_Parameters
{
 /// Define Poisson's ratio Nu
 std::complex<double> Nu(0.3,0.0);
 
 /// Define the non-dimensional Young's modulus
 std::complex<double> E(1.0,0.0);
 
 /// Define Fourier wavenumber
 int Fourier_wavenumber = 0;
 
 /// Define the non-dimensional square angular frequency of 
 /// time-harmonic motion
 std::complex<double> Omega_sq (10.0,0.0);
 
 /// Length of domain in r direction
 double Lr = 1.0;
 
 /// Length of domain in z-direction
 double Lz = 2.0;
 
 // Set up min & max (r,z) coordinates
 double rmin = 0.1;
 double zmin = 0.3;
 double rmax = rmin+Lr;
 double zmax = zmin+Lz;
 
 /// Define the imaginary unit
 const std::complex<double> I(0.0,1.0);
 
 // Pressure load
 double P=1.0;
 
 /// The traction function at r=rmin: (t_r, t_z, t_theta)
 void boundary_traction(const Vector<double> &x,
                      const Vector<double> &n,
                      Vector<std::complex<double> > &result)
 {
  // Radial traction
  result[0] = P;
  // Axial traction
  result[1] = 0.0;
  // Azimuthal traction
  result[2] = 0.0;
 }
 
 
} // end_of_namespace
 
 
//===start_of_problem_class=============================================
/// Class to validate time harmonic linear elasticity (Fourier 
/// decomposed)
//======================================================================
template<class ELEMENT>
class FourierDecomposedTimeHarmonicLinearElasticityProblem : public Problem
{
public:
 
 /// Constructor: Pass number of elements in r and z directions 
 /// and boundary locations
 FourierDecomposedTimeHarmonicLinearElasticityProblem(
 const unsigned &nr, const unsigned &nz,
 const double &rmin, const double& rmax,
 const double &zmin, const double& zmax);
 
 
 /// Update before solve is empty
 void actions_before_newton_solve() {}
 
 /// Update after solve is empty
 void actions_after_newton_solve() {}
 
 /// Delete traction elements
 void delete_traction_elements();
 
 /// Helper function to complete problem setup
 void complete_problem_setup();
 
 /// Actions before adapt: Wipe the mesh of traction elements
 void actions_before_adapt()
  {
   // Kill the traction elements and wipe surface mesh
   delete_traction_elements();
   
   // Rebuild the Problem's global mesh from its various sub-meshes
   rebuild_global_mesh();
  }
 
 
 /// Actions after adapt: Rebuild the mesh of traction elements
 void actions_after_adapt()
  {
   // Create traction elements from all elements that are 
   // adjacent to FSI boundaries and add them to surface meshes
   assign_traction_elements();
   
   // Rebuild the Problem's global mesh from its various sub-meshes
   rebuild_global_mesh();
   
   // Complete problem setup
   complete_problem_setup();   
  }
 
 /// Doc the solution
 void doc_solution(DocInfo& doc_info);
 
private:
 
 /// Allocate traction elements on the bottom surface
 void assign_traction_elements();
 
#ifdef ADAPTIVE
 
 /// Pointer to the bulk mesh
 RefineableTriangleMesh<ELEMENT>* Bulk_mesh_pt;
 
#else
 
 /// Pointer to the bulk mesh
 Mesh* Bulk_mesh_pt;
 
#endif
 
 /// Pointer to the mesh of traction elements
 Mesh* Surface_mesh_pt;
}; // end_of_problem_class
 
 
//===start_of_constructor=============================================
/// Problem constructor: Pass number of elements in coordinate
/// directions and size of domain.
//====================================================================
template<class ELEMENT>
FourierDecomposedTimeHarmonicLinearElasticityProblem<ELEMENT>::
FourierDecomposedTimeHarmonicLinearElasticityProblem
(const unsigned &nr, const unsigned &nz,
 const double &rmin, const double& rmax,
 const double &zmin, const double& zmax)
{
 
#ifdef ADAPTIVE
 
 // The boundary is bounded by four distinct boundaries, each
 // represented by its own polyline
 Vector<TriangleMeshCurveSection*> boundary_polyline_pt(4);
 
 // Vertex coordinates on boundary
 Vector<Vector<double> > bound_coords(2);
 bound_coords[0].resize(2);
 bound_coords[1].resize(2);
     
 // Horizontal bottom boundary
 bound_coords[0][0]=rmin;
 bound_coords[0][1]=zmin;
 bound_coords[1][0]=rmax;
 bound_coords[1][1]=zmin;
 
 // Build the boundary polyline
 unsigned boundary_id=0;
 boundary_polyline_pt[0]=new TriangleMeshPolyLine(bound_coords,boundary_id);
 
 // Vertical outer boundary
 bound_coords[0][0]=rmax;
 bound_coords[0][1]=zmin;
 bound_coords[1][0]=rmax;
 bound_coords[1][1]=zmax;
 
 // Build the boundary polyline
 boundary_id=1;
 boundary_polyline_pt[1]=new TriangleMeshPolyLine(bound_coords,boundary_id);
 
 
 // Horizontal top boundary
 bound_coords[0][0]=rmax;
 bound_coords[0][1]=zmax;
 bound_coords[1][0]=rmin;
 bound_coords[1][1]=zmax;
 
 // Build the boundary polyline
 boundary_id=2;
 boundary_polyline_pt[2]=new TriangleMeshPolyLine(bound_coords,boundary_id);
 
 // Vertical inner boundary
 bound_coords[0][0]=rmin;
 bound_coords[0][1]=zmax;
 bound_coords[1][0]=rmin;
 bound_coords[1][1]=zmin;
 
 // Build the boundary polyline
 boundary_id=3;
 boundary_polyline_pt[3]=new TriangleMeshPolyLine(bound_coords,boundary_id);
 
 // Pointer to the closed curve that defines the outer boundary
 TriangleMeshClosedCurve* closed_curve_pt= 
  new TriangleMeshPolygon(boundary_polyline_pt);
  
 // Use the TriangleMeshParameters object for helping on the manage of the
 // TriangleMesh parameters
 TriangleMeshParameters triangle_mesh_parameters(closed_curve_pt);
 
 // Specify the maximum area element
 double uniform_element_area=0.2;
 triangle_mesh_parameters.element_area() = uniform_element_area;
 
 // Create the mesh
 Bulk_mesh_pt=new RefineableTriangleMesh<ELEMENT>(triangle_mesh_parameters);
 
 // Set error estimator
 Bulk_mesh_pt->spatial_error_estimator_pt()=new Z2ErrorEstimator;
 
#else
 
 //Now create the mesh
 Bulk_mesh_pt = new RectangularQuadMesh<ELEMENT>(nr,nz,rmin,rmax,zmin,zmax);
 
#endif
 
 //Create the surface mesh of traction elements
 Surface_mesh_pt=new Mesh;
 assign_traction_elements();
 
 // Complete problem setup
 complete_problem_setup();
 
 // Add the submeshes to the problem
 add_sub_mesh(Bulk_mesh_pt);
 add_sub_mesh(Surface_mesh_pt);
 
 // Now build the global mesh
 build_global_mesh();
 
 // Assign equation numbers
 cout << assign_eqn_numbers() << " equations assigned" << std::endl; 
 
} // end of constructor
 
 
 
//===start_of_complete_problem_setup=================================
/// Complete problem setup
//===================================================================
template<class ELEMENT>
void FourierDecomposedTimeHarmonicLinearElasticityProblem<ELEMENT>::
complete_problem_setup()
{
 // Set the boundary conditions for this problem: All nodes are
 // free by default -- just pin & set the ones that have Dirichlet 
 // conditions here
 
 // Pin displacements everywhere apart from boundaries 1 and 3
 //-----------------------------------------------------------
 for (unsigned ibound=0;ibound<3;ibound=ibound+2)
  {
   unsigned num_nod=Bulk_mesh_pt->nboundary_node(ibound);
   for (unsigned inod=0;inod<num_nod;inod++) 
    {
     // Get pointer to node
     Node* nod_pt=Bulk_mesh_pt->boundary_node_pt(ibound,inod);
     
     // Pinned in r, z and theta
     nod_pt->pin(0);nod_pt->pin(1);nod_pt->pin(2);
     nod_pt->pin(3);nod_pt->pin(4);nod_pt->pin(5);
     
     // Set the displacements
     nod_pt->set_value(0,0.0);
     nod_pt->set_value(1,0.0);
     nod_pt->set_value(2,0.0);
     nod_pt->set_value(3,0.0);
     nod_pt->set_value(4,0.0);
     nod_pt->set_value(5,0.0);
    }
  }
 
 
 // Complete the problem setup to make the elements fully functional
 
 // Loop over the elements
 unsigned n_el = Bulk_mesh_pt->nelement();
 for(unsigned e=0;e<n_el;e++)
  {
   // Cast to a bulk element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(Bulk_mesh_pt->element_pt(e));
 
   // Set the pointer to Poisson's ratio
   el_pt->nu_pt() = &Global_Parameters::Nu;
 
   // Set the pointer to Fourier wavenumber
   el_pt->fourier_wavenumber_pt() = &Global_Parameters::Fourier_wavenumber;
 
   // Set the pointer to non-dim Young's modulus
   el_pt->youngs_modulus_pt() = &Global_Parameters::E;
 
   // Set the pointer to square of the angular frequency
   el_pt->omega_sq_pt() = &Global_Parameters::Omega_sq;
 
  }// end loop over elements
 
 // Loop over the traction elements
 unsigned n_traction =  Surface_mesh_pt->nelement();
 for(unsigned e=0;e<n_traction;e++)
  {
   // Cast to a surface element
   TimeHarmonicFourierDecomposedLinearElasticityTractionElement<ELEMENT>*
    el_pt = 
    dynamic_cast<TimeHarmonicFourierDecomposedLinearElasticityTractionElement
    <ELEMENT>* >(Surface_mesh_pt->element_pt(e));
   
   // Set the applied traction
   el_pt->traction_fct_pt() = &Global_Parameters::boundary_traction;
   
  }// end loop over traction elements
 
}
 
//===start_of_traction===============================================
/// Make traction elements along the boundary r=rmin
//===================================================================
template<class ELEMENT>
void FourierDecomposedTimeHarmonicLinearElasticityProblem<ELEMENT>::
assign_traction_elements()
{
 unsigned bound, n_neigh;
 
 // How many bulk elements are next to boundary 3
 bound=3;
 n_neigh = Bulk_mesh_pt->nboundary_element(bound); 
 
 // Now loop over bulk elements and create the face elements
 for(unsigned n=0;n<n_neigh;n++)
  {
   // Create the face element
   FiniteElement *traction_element_pt 
    = new TimeHarmonicFourierDecomposedLinearElasticityTractionElement<ELEMENT>
    (Bulk_mesh_pt->boundary_element_pt(bound,n),
     Bulk_mesh_pt->face_index_at_boundary(bound,n));
 
   // Add to mesh
   Surface_mesh_pt->add_element_pt(traction_element_pt);
  }
 
} // end of assign_traction_elements
 
 
//===start_of_delete_traction========================================
/// Delete traction elements
//===================================================================
template<class ELEMENT>
void FourierDecomposedTimeHarmonicLinearElasticityProblem<ELEMENT>::
delete_traction_elements()
{
 // How many surface elements are in the surface mesh
 unsigned n_element = Surface_mesh_pt->nelement();
 
 // Loop over the surface elements
 for(unsigned e=0;e<n_element;e++)
  {
   // Kill surface element
   delete Surface_mesh_pt->element_pt(e);
  }
 
 // Wipe the mesh
 Surface_mesh_pt->flush_element_and_node_storage();
 
} // end of delete_traction_elements
 
 
//==start_of_doc_solution=================================================
/// Doc the solution
//========================================================================
template<class ELEMENT>
void FourierDecomposedTimeHarmonicLinearElasticityProblem<ELEMENT>::
doc_solution(DocInfo& doc_info)
{ 
 ofstream some_file;
 char filename[100];
 
 // Number of plot points
 unsigned npts=5; 
 
 // Output solution 
 sprintf(filename,"%s/soln.dat",doc_info.directory().c_str());
 some_file.open(filename);
 Bulk_mesh_pt->output(some_file,npts);
 some_file.close();
 
 // Output norm of solution (to allow validation of solution even
 // if triangle generates a slightly different mesh)
 sprintf(filename,"%s/norm.dat",doc_info.directory().c_str());   
 some_file.open(filename);   
 double norm=0.0;
 unsigned nel=Bulk_mesh_pt->nelement();
 for (unsigned e=0;e<nel;e++)
  {
   double el_norm=0.0;
   Bulk_mesh_pt->compute_norm(el_norm);
   norm+=el_norm;
  }
 some_file << norm << std::endl;
 
 
} // end_of_doc_solution   
 
 
//===start_of_main======================================================
/// Driver code 
//======================================================================
int main(int argc, char* argv[]) 
{
 // Number of elements in r-direction
 unsigned nr=10;
 
 // Number of elements in z-direction (for (approximately) square elements)
 unsigned nz=unsigned(double(nr)*Global_Parameters::Lz/Global_Parameters::Lr);
 
 // Set up doc info
 DocInfo doc_info;
 
 // Set output directory
 doc_info.set_directory("RESLT");
 
#ifdef ADAPTIVE
 
 // Set up problem
 FourierDecomposedTimeHarmonicLinearElasticityProblem
  <ProjectableTimeHarmonicFourierDecomposedLinearElasticityElement
   <TTimeHarmonicFourierDecomposedLinearElasticityElement<3> > >
  problem(nr,nz,Global_Parameters::rmin,Global_Parameters::rmax,
          Global_Parameters::zmin,Global_Parameters::zmax);
 
 // Solve
 unsigned max_adapt=3;
 problem.newton_solve(max_adapt);
 
#else
 
 // Set up problem
 FourierDecomposedTimeHarmonicLinearElasticityProblem
  <QTimeHarmonicFourierDecomposedLinearElasticityElement<3> > 
  problem(nr,nz,Global_Parameters::rmin,Global_Parameters::rmax,
          Global_Parameters::zmin,Global_Parameters::zmax);
 
 // Solve
 problem.newton_solve();
 
#endif
 
 // Output the solution
 problem.doc_solution(doc_info);
  
} // end_of_main

Source files for this tutorial

The source files for this tutorial are located in the directory: demo_drivers/time_harmonic_fourier_decomposed_linear_elasticity/cylinder/
The driver code is: demo_drivers/time_harmonic_fourier_decomposed_linear_elasticity/cylinder/pressure_loaded_cylinder.cc

PDF file

A pdf version of this document is available.