In this tutorial we demonstrate the adaptive solution of free surface problems on unstructured meshes, using the example of a bubble propagating along a straight channel. We also demonstrate how to impose volume constraints on enclosed regions within the fluid.

The example problem

We illustrate the solution of the unsteady 2D Navier-Stokes equations by considering the propagation of a single bubble along a straight channel as shown in the sketch below. We non-dimensionalise all lengths on the channel width, $\mathcal{L}=H$ , velocities on the maximum (prescribed) inflow velocity, $\mathcal{U}$ , and time on the intrinsic timescale, $\mathcal{T}=\mathcal{L}/\mathcal{U}$ , which corresponds to a Strouhal number .

The problem setup.

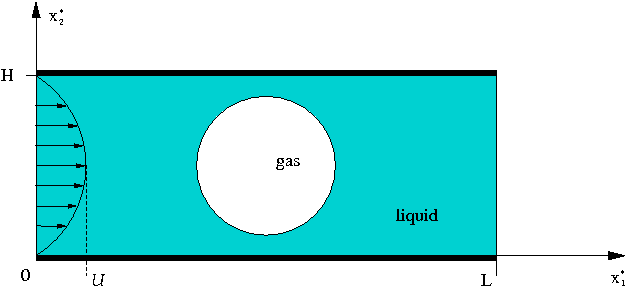
The problem is then governed by the following equations.

Solve

$Re\Big(St\frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial x_j} \Big) = - \frac{\partial p}{\partial x_i} + \frac{\partial }{\partial x_j} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right), \ \ \ \ \ \ \ \ \ \ (1)$

and

$\frac{\partial u_i}{\partial x_i} = 0,$

in the rectangular domain $D = \left\{x_1 \in [0,1]; x_2 \in [0,L] \right\}$ , subject to the Dirichlet boundary conditions

$u_1=0, \ \ \ \ \ \ \ \ \ \ (2)$

on the top and bottom boundaries and

$u_2=0, \ \ \ \ \ \ \ \ \ \ (3)$

on all boundaries. The inflow on the left boundary is described by a Poiseuille flow profile

$u_1(x_2)=4 x_2 (1-x_2). \ \ \ \ \ \ \ \ \ \ (4)$

The free surface is defined by the position vector $\mathbf{R}$ , which is subject to the kinematic condition

$\Big(u_i-St \frac{\partial R_i}{\partial t} \Big) n_i =0, \ \ \ \ \ \ \ \ \ \ (5)$

and the dynamic condition

$\tau_{ij} n_j=- \Big( \frac{1}{Ca} \kappa+p_{bubble} \Big) n_i, \ \ \ \ \ \ \ \ \ \ (6)$

where the stress tensor is defined as

$\tau_{ij}=-p \delta_{ij}+\Big( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \Big). \ \ \ \ \ \ \ \ \ \ (7)$

The initial position of the interface, for a bubble initially located in the centre of the channel, is given by

$\mathbf{R}(\zeta)=\Big( \frac{L}{2}+ a \frac{1-\zeta^2}{1+\zeta^2}, \frac{1}{2} + a \frac{2\zeta}{1+\zeta^2} \Big), \ \ \ \ \ \ \ \ \ \ (8)$

where is the initial non-dimensional bubble radius and $\zeta=[0,2\pi]$ .

The problem is subject to the constraint that the bubble volume, $V_{bubble}$ , remains constant which is achieved by adjusting, the bubble pressure, $p_{bubble}$ . We formulate the volume constraint by making use of Gauss` theorem, which states that for any vector $\mathbf{b}$

$\int \nabla . \mathbf{b} dV = \oint \mathbf{b}. \mathbf{n} dS. \ \ \ \ \ \ \ \ \ \ (9)$

Choosing $\mathbf{b}=\mathbf{x}$ we note that the divergence of $\mathbf{x}$ gives the spatial dimension and the integral $\int dV$ is the enclosed volume $V_{bubble}$ . Hence, the volume constraint can be written as

$V_{bubble}-\frac{1}{D} \oint \mathbf{R}.\mathbf{n} dS=0. \ \ \ \ \ \ \ \ \ \ (10)$

This is the equation that determines the unknown bubble pressure $p_{bubble}$ .

Implementation

We solve the governing equations using an ALE-based finite-element method, discretising the fluid domain with triangular Taylor-Hood elements, and updating the mesh with a pseudo-elastic node-update procedure.
As usual, we impose the kinematic and dynamic boundary conditions with FaceElements. The volume constraint is imposed in a similar way: We attach LineVolumeConstraintBoundingSolidElements to the bubble surface to compute the line integrals in equation (10), and create an additional VolumeConstraintElement which adds $V_{bubble}$ to this equation and is also "in charge" of the unknown bubble pressure.

Results

We perform the simulation in a two-stage procedure. We start by performing a steady solve with the inflow switched off. This deforms the bubble into its steady state (approximately) circular configuration with the required volume. The actual time-dependent simulation is then performed with an impulsive start from this configuration.

The figure below shows a contour plot of the pressure distribution with overlaid streamlines. This is a snapshot of an animation of the flow field, for the parameters and .

Snapshot of the flow field (streamlines and pressure contours) for a propagating bubble.

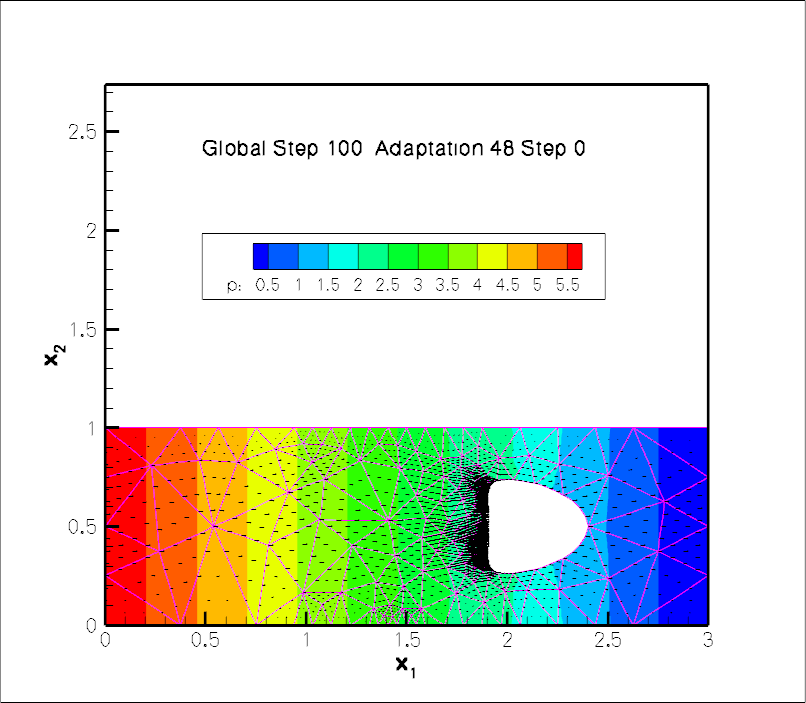
Global parameters

As usual, we create a namespace where we define the dimensionless parameters , and the non-dimensional channel length . As discussed in another tutorial, the Strouhal number defaults to one, so that we do not have to set it in this case. We also store the initial bubble radius and the bubble volume, as well as a scaling factor for the inflow velocity (this allows us to "switch off" the inflow when computing the initial steady solution). Finally we define the Poisson ratio for the generalised Hookean constitutive law that is used by pseudo-elastic mesh update.

//==start_of_namespace==============================
/// Namespace for Problem Parameter
//==================================================
 namespace Problem_Parameter
 {    
  /// Doc info object
  DocInfo Doc_info;
  
  /// Reynolds number
  double Re=0.0;
 
  /// Capillary number
  double Ca = 10.0;
 
  /// Pseudo-solid Poisson ratio
  double Nu=0.3;
 
  /// Initial radius of bubble
  double Radius = 0.25;
 
  /// Volume of the bubble (negative because it's outside the
  /// fluid!)
  double Volume = -MathematicalConstants::Pi*Radius*Radius;
 
  /// Scaling factor for inflow velocity (allows it to be switched off
  /// to do hydrostatics)
  double Inflow_veloc_magnitude = 0.0;
 
  /// Length of the channel
  double Length = 3.0;
 
  /// Constitutive law used to determine the mesh deformation
  ConstitutiveLaw *Constitutive_law_pt=0;
 
  /// Trace file
  ofstream Trace_file;
 
  /// File to document the norm of the solution (for validation 
  /// purposes -- triangle doesn't give fully reproducible results so
  /// mesh generation/adaptation may generate slightly different numbers
  /// of elements on different machines!)
  ofstream Norm_file;
  
 } // end_of_namespace

The driver code

We start by processing the command line arguments and create the generalised Hookean constitutive equations for the pseudo-elastic node-update. We then open various output files and build the problem.

//==========start_of_main=====================================
/// Driver code for moving bubble problem
//============================================================
int main(int argc, char **argv)
{
  
 // Store command line arguments
 CommandLineArgs::setup(argc,argv);
 
 // Define possible command line arguments and parse the ones that
 // were actually specified
 
 // Validation?
 CommandLineArgs::specify_command_line_flag("--validation");
 
 // Parse command line
 CommandLineArgs::parse_and_assign(); 
 
 // Doc what has actually been specified on the command line
 CommandLineArgs::doc_specified_flags();
 
 // Create generalised Hookean constitutive equations
 Problem_Parameter::Constitutive_law_pt = 
  new GeneralisedHookean(&Problem_Parameter::Nu);
 
 // Open trace file
 Problem_Parameter::Trace_file.open("RESLT/trace.dat"); 
 
 // Increase precision of output
 Problem_Parameter::Trace_file.precision(20);
 
 // Open norm file
 Problem_Parameter::Norm_file.open("RESLT/norm.dat");
 
 
 // Create problem in initial configuration
 BubbleInChannelProblem<ProjectableTaylorHoodElement<MyTaylorHoodElement> > 

We start by performing a steady solve (with the inflow switched off) to compute the initial configuration, a circular bubble in stationary fluid.

 // Before starting the time-integration we want to "inflate" it to form 
 // a proper circular bubble. We do this by setting the inflow to zero
 // and doing a steady solve (with one adaptation)
 Problem_Parameter::Inflow_veloc_magnitude=0.0;
 
 problem.steady_newton_solve(1);
 
 // If all went well, this should show us a nice circular bubble
 // in a stationary fluid
 problem.doc_solution();

Next, the timestepper is initialised and an impulsive start performed. The inflow is switched on and the first few unsteady Newton solves are performed without adaptation.

 // Initialise timestepper
 double dt=0.025;
 problem.initialise_dt(dt);
 
 // Perform impulsive start from current state
 problem.assign_initial_values_impulsive();
 
 
 // Now switch on the inflow and re-assign the boundary conditions
 // (Call to complete_problem_setup() is a bit expensive given that we
 // we only want to set the inflow velocity but who cares -- it's just
 // a one off.
 Problem_Parameter::Inflow_veloc_magnitude=1.0;
 problem.complete_problem_setup();
 
 
 // Solve problem on fixed mesh
 unsigned nstep=6;
 if (CommandLineArgs::command_line_flag_has_been_set("--validation"))
  {
   nstep=2;
   oomph_info << "Remeshing after every second step during validation\n";
  }
 for (unsigned i=0;i<nstep;i++)
  {
   // Solve the problem
   problem.unsteady_newton_solve(dt);    
   problem.doc_solution();
  } // done solution on fixed mesh

To limit the distortion of the elements we allow then mesh adaptation (which involves the re-generation of the entire mesh) every few timesteps.

 // Now do a proper loop, doing nstep timesteps before adapting/remeshing
 // and repeating the lot ncycle times
 unsigned ncycle=1000;
 if (CommandLineArgs::command_line_flag_has_been_set("--validation"))
  {
   ncycle=1;
   oomph_info << "Only doing one cycle during validation\n";
  }
 
 // Do the cycles
 for(unsigned j=0;j<ncycle;j++)
  {       
   // Allow up to one level of refinement for next solve
   unsigned max_adapt=1;
 
   //Solve problem a few times
   for (unsigned i=0;i<nstep;i++)
    {     
     // Solve the problem
     problem.unsteady_newton_solve(dt,max_adapt,false); 
 
 
     // Build the label for doc and output solution
     std::stringstream label;
     label << "Adaptation " <<j << " Step "<< i;
     problem.doc_solution(label.str());
 
     // No more refinement for the next nstep steps
     max_adapt=0;
    }
 
  }
 
 
} //End of main

The problem class

As usual, we template the Problem class by the element type

//==start_of_problem_class============================================
/// Problem class to simulate inviscid bubble propagating along 2D channel
//====================================================================
template<class ELEMENT>
class BubbleInChannelProblem : public Problem
{
 
public:
 
 /// Constructor
 BubbleInChannelProblem();
 
 /// Destructor
 ~BubbleInChannelProblem()

The FaceElements are deleted and re-attached before and after each adaptation. Also, as discussed in another tutorial, we re-apply the boundary conditions and complete the build of all elements after each adaptation, using the helper function complete_problem_setup() (discussed below).

 /// Actions before adapt: Wipe the mesh of free surface elements
 void actions_before_adapt()
  {
   // Kill the  elements and wipe surface mesh
   delete_free_surface_elements();
   delete_volume_constraint_elements();
 
   // Rebuild the Problem's global mesh from its various sub-meshes
   this->rebuild_global_mesh();
  
  }// end of actions_before_adapt
 
 
 /// Actions after adapt: Rebuild the mesh of free surface elements
 void actions_after_adapt()
  {
   // Create the elements that impose the displacement constraint 
   create_free_surface_elements();
   create_volume_constraint_elements();
   
   // Rebuild the Problem's global mesh from its various sub-meshes
   this->rebuild_global_mesh();
   
   // Setup the problem again -- remember that fluid mesh has been
   // completely rebuilt and its element's don't have any
   // pointers to Re etc. yet
   complete_problem_setup();
 
  }// end of actions_after_adapt
 
 
 /// Update the after solve (empty)
 void actions_after_newton_solve(){}
 
 /// Update the problem specs before solve
 void actions_before_newton_solve()
  {
   //Reset the Lagrangian coordinates of the nodes to be the current
   //Eulerian coordinates -- this makes the current configuration
   //stress free
   Fluid_mesh_pt->set_lagrangian_nodal_coordinates();
  }
 
 /// Set boundary conditions and complete the build of all elements
 void complete_problem_setup();

We define the post-processing functions to document the solution and to compute the error estimates.

 /// Doc the solution
 void doc_solution(const std::string& comment="");
 
 /// Compute the error estimates and assign to elements for plotting
 void compute_error_estimate(double& max_err,

We also provide helper functions to delete and create face elements adjacent to the bubble boundary.

private:
 
 
 /// Create free surface elements
 void create_free_surface_elements();
 
 /// Delete free surface elements 
 void delete_free_surface_elements()
  {
   // How many surface elements are in the surface mesh
   unsigned n_element = Free_surface_mesh_pt->nelement();
   
   // Loop over the surface elements
   for(unsigned e=0;e<n_element;e++)
    {
     // Kill surface element
     delete Free_surface_mesh_pt->element_pt(e);
    }
   
   // Wipe the mesh
   Free_surface_mesh_pt->flush_element_and_node_storage();
   
  } // end of delete_free_surface_elements
 
 
/// Create elements that impose volume constraint on the bubble
 void create_volume_constraint_elements();
 
 /// Delete volume constraint elements
 void delete_volume_constraint_elements()
  {
   // How many surface elements are in the surface mesh
   unsigned n_element = Volume_constraint_mesh_pt->nelement();
   
   // Loop over the surface elements (but don't kill the volume constraint
   // element (element 0))
   unsigned first_el_to_be_killed=1;
   for(unsigned e=first_el_to_be_killed;e<n_element;e++) 
    {
     delete Volume_constraint_mesh_pt->element_pt(e);
    }
   
   // Wipe the mesh
   Volume_constraint_mesh_pt->flush_element_and_node_storage();
   
  } // end of delete_volume_constraint_elements

The private data includes pointers to the fluid mesh, and the two face meshes which impose the kinematic and dynamic boundary conditions, and the volume constraint, respectively. We also store pointers to the Data that stores the unknown bubble pressure and to the VolumeConstraintElement that imposes the volume constraint and is "in charge of" the bubble pressure.

 /// Pointers to mesh of free surface elements
 Mesh* Free_surface_mesh_pt;
 
 /// Pointer to mesh containing elements that impose volume constraint
 Mesh* Volume_constraint_mesh_pt;
 
 /// Pointer to Fluid_mesh
 RefineableSolidTriangleMesh<ELEMENT>* Fluid_mesh_pt;
 
 /// Vector storing pointer to the bubble polygons
 Vector<TriangleMeshPolygon*> Bubble_polygon_pt;
 
 /// Triangle mesh polygon for outer boundary 
 TriangleMeshPolygon* Outer_boundary_polyline_pt; 
 
 /// Pointer to a global bubble pressure datum
 Data* Bubble_pressure_data_pt;
 
 /// Pointer to element that imposes volume constraint for bubble
 VolumeConstraintElement* Vol_constraint_el_pt;
 
 /// Enumeration of mesh boundaries
 enum 
 {
  Inflow_boundary_id=0,
  Upper_wall_boundary_id=1,
  Outflow_boundary_id=2,
  Bottom_wall_boundary_id=3,
  First_bubble_boundary_id=4,
  Second_bubble_boundary_id=5
 };
 
 
}; // end_of_problem_class

The problem constructor

We allocate the timestepper and build the VolumeConstraintElement that imposes the volume constraint. The element stores the volume that is to be conserved as well as the bubble pressure, which is determined from the volume constraint. The initial guess for the bubble pressure, $p_{bubble}=Ca/a$ , is appropriate for a static bubble in stationary fluid.

//==start_constructor=====================================================
/// Constructor
//========================================================================
template<class ELEMENT>
BubbleInChannelProblem<ELEMENT>::BubbleInChannelProblem()
{ 
 // Output directory
 Problem_Parameter::Doc_info.set_directory("RESLT");
 
 // Allocate the timestepper -- this constructs the Problem's 
 // time object with a sufficient amount of storage to store the
 // previous timsteps. 
 this->add_time_stepper_pt(new BDF<2>);
 
 
 
 // Build volume constraint element: Pass pointer to double that
 // specifies target volume, data that contains the "traded" pressure
 // and the index of the traded pressure value within this Data item
 // Build element and create pressure internally
 Vol_constraint_el_pt= 
  new VolumeConstraintElement(&Problem_Parameter::Volume);
 
 // Which value stores the pressure?
 unsigned index=Vol_constraint_el_pt->index_of_traded_pressure();
 
 // Pressure data
 Bubble_pressure_data_pt=Vol_constraint_el_pt->p_traded_data_pt();
 
 // Assign initial value
 Vol_constraint_el_pt->p_traded_data_pt()->
  set_value(index,Problem_Parameter::Ca/Problem_Parameter::Radius);

Next the outer boundary, consisting of four separate polylines, is built. Each polyline is defined by a start and an end point and is stored in a vector. This vector is then used to create the closed polygon required by Triangle.

 // Build the boundary segments for outer boundary, consisting of
 //--------------------------------------------------------------
 // four separate polylines
 //------------------------
 Vector<TriangleMeshCurveSection*> boundary_polyline_pt(4);
 
 // Each polyline only has two vertices -- provide storage for their
 // coordinates
 Vector<Vector<double> > vertex_coord(2);
 for(unsigned i=0;i<2;i++)
  {
   vertex_coord[i].resize(2);
  }
 
 // First polyline: Inflow
 vertex_coord[0][0]=0.0;
 vertex_coord[0][1]=0.0;
 vertex_coord[1][0]=0.0;
 vertex_coord[1][1]=1.0;
 
 // Build the 1st boundary polyline
 boundary_polyline_pt[0] = new TriangleMeshPolyLine(vertex_coord,
                                                   Inflow_boundary_id);
 
 // Second boundary polyline: Upper wall
 vertex_coord[0][0]=0.0;
 vertex_coord[0][1]=1.0;
 vertex_coord[1][0]=Problem_Parameter::Length;
 vertex_coord[1][1]=1.0;
 
 // Build the 2nd boundary polyline
 boundary_polyline_pt[1] = new TriangleMeshPolyLine(vertex_coord,
                                                   Upper_wall_boundary_id);
 
 // Third boundary polyline: Outflow
 vertex_coord[0][0]=Problem_Parameter::Length;
 vertex_coord[0][1]=1.0;
 vertex_coord[1][0]=Problem_Parameter::Length;
 vertex_coord[1][1]=0.0;
 
 // Build the 3rd boundary polyline
 boundary_polyline_pt[2] = new TriangleMeshPolyLine(vertex_coord,
                                                   Outflow_boundary_id);
 
 // Fourth boundary polyline: Bottom wall
 vertex_coord[0][0]=Problem_Parameter::Length;
 vertex_coord[0][1]=0.0;
 vertex_coord[1][0]=0.0;
 vertex_coord[1][1]=0.0;
 
 // Build the 4th boundary polyline
 boundary_polyline_pt[3] = new TriangleMeshPolyLine(vertex_coord,
                                                    Bottom_wall_boundary_id);
 
 // Create the triangle mesh polygon for outer boundary
 Outer_boundary_polyline_pt = new TriangleMeshPolygon(boundary_polyline_pt);

Next the polygon representing the bubble in the initial setup is generated. (Recall that closed polygons must be subdivided into at least two distinct polylines.)

 // Now define initial shape of bubble(s) with polygon
 //---------------------------------------------------
 
 // We have one bubble
 Bubble_polygon_pt.resize(1);
 
 // Place it smack in the middle of the channel
 double x_center = 0.5*Problem_Parameter::Length;
 double y_center = 0.5;
 Ellipse * bubble_pt = new Ellipse(Problem_Parameter::Radius,
                                       Problem_Parameter::Radius);
 
 // Intrinsic coordinate along GeomObject defining the bubble
 Vector<double> zeta(1);
 
 // Position vector to GeomObject defining the bubble
 Vector<double> coord(2);
 
 // Number of points defining bubble
 unsigned npoints = 16; 
 double unit_zeta = MathematicalConstants::Pi/double(npoints-1);
 
 // This bubble is bounded by two distinct boundaries, each
 // represented by its own polyline
 Vector<TriangleMeshCurveSection*> bubble_polyline_pt(2);
 
 // Vertex coordinates
 Vector<Vector<double> > bubble_vertex(npoints);
 
 // Create points on boundary
 for(unsigned ipoint=0; ipoint<npoints;ipoint++)
  {
   // Resize the vector 
   bubble_vertex[ipoint].resize(2);
   
   // Get the coordinates
   zeta[0]=unit_zeta*double(ipoint);
   bubble_pt->position(zeta,coord);
 
   // Shift
   bubble_vertex[ipoint][0]=coord[0]+x_center;
   bubble_vertex[ipoint][1]=coord[1]+y_center;
  }
 
 // Build the 1st bubble polyline
 bubble_polyline_pt[0] = new TriangleMeshPolyLine(bubble_vertex,
                                                  First_bubble_boundary_id);
 
 // Second boundary of bubble
 for(unsigned ipoint=0; ipoint<npoints;ipoint++)
  {
   // Resize the vector 
   bubble_vertex[ipoint].resize(2);
   
   // Get the coordinates
   zeta[0]=(unit_zeta*double(ipoint))+MathematicalConstants::Pi;
   bubble_pt->position(zeta,coord);
 
   // Shift
   bubble_vertex[ipoint][0]=coord[0]+x_center;
   bubble_vertex[ipoint][1]=coord[1]+y_center;
  }
 
 // Build the 2nd bubble polyline
 bubble_polyline_pt[1] = new TriangleMeshPolyLine(bubble_vertex,
                                                  Second_bubble_boundary_id);
 
 
 // Define coordinates of a point inside the bubble
 Vector<double> bubble_center(2);
 bubble_center[0]=x_center;
 bubble_center[1]=y_center;
 
 
 // Create closed polygon from two polylines
 Bubble_polygon_pt[0] = new TriangleMeshPolygon(
                 bubble_polyline_pt,
                 bubble_center);

Once the boundary representation in form of polygons is completed the mesh is generated using Triangle. We specify the error estimator and set targets for the spatial adaptivity, and output the initial mesh.

 // Now build the mesh, based on the boundaries specified by
 //---------------------------------------------------------
 // polygons just created
 //----------------------
 
 // Convert to "closed curve" objects
 TriangleMeshClosedCurve* outer_closed_curve_pt=Outer_boundary_polyline_pt;
 unsigned nb=Bubble_polygon_pt.size();
 Vector<TriangleMeshClosedCurve*> bubble_closed_curve_pt(nb);
 for (unsigned i=0;i<nb;i++)
  {
   bubble_closed_curve_pt[i]=Bubble_polygon_pt[i];
  }
 
 // Target area for initial mesh
 double uniform_element_area=0.2;
 
 // Use the TriangleMeshParameters object for gathering all
 // the necessary arguments for the TriangleMesh object
 TriangleMeshParameters triangle_mesh_parameters(
   outer_closed_curve_pt);
 
 // Define the holes on the boundary
 triangle_mesh_parameters.internal_closed_curve_pt() =
   bubble_closed_curve_pt;
 
 // Define the maximum element areas
 triangle_mesh_parameters.element_area() =
   uniform_element_area;
 
 // Create the mesh
 Fluid_mesh_pt =
   new RefineableSolidTriangleMesh<ELEMENT>(
     triangle_mesh_parameters, this->time_stepper_pt());
 
 // Set error estimator for bulk mesh
 Z2ErrorEstimator* error_estimator_pt=new Z2ErrorEstimator;
 Fluid_mesh_pt->spatial_error_estimator_pt()=error_estimator_pt;
 
 // Set targets for spatial adaptivity
 Fluid_mesh_pt->max_permitted_error()=0.005;
 Fluid_mesh_pt->min_permitted_error()=0.001;
 Fluid_mesh_pt->max_element_size()=0.2;
 Fluid_mesh_pt->min_element_size()=0.001; 
 
 // Use coarser mesh during validation
 if (CommandLineArgs::command_line_flag_has_been_set("--validation"))
  {
   Fluid_mesh_pt->min_element_size()=0.01; 
  }
 
 // Output boundary and mesh initial mesh for information
 this->Fluid_mesh_pt->output_boundaries("boundaries.dat");
 this->Fluid_mesh_pt->output("mesh.dat");

We complete the problem setup, create the various surface meshes that impose the dynamic and kinematic boundary conditions and the volume constraint. We then combine the submeshes into a global mesh.

 // Set boundary condition and complete the build of all elements
 complete_problem_setup();
 
 // Construct the mesh of free surface elements
 Free_surface_mesh_pt=new Mesh;
 create_free_surface_elements();
 
 // Construct the mesh of elements that impose the volume constraint
 Volume_constraint_mesh_pt = new Mesh;
 create_volume_constraint_elements();
 
 // Combine meshes
 //---------------
 
 // Add volume constraint sub mesh
 this->add_sub_mesh(this->Volume_constraint_mesh_pt);
 
 // Add Fluid_mesh_pt sub meshes
 this->add_sub_mesh(Fluid_mesh_pt);
 
 // Add Free_surface sub meshes
 this->add_sub_mesh(this->Free_surface_mesh_pt);
 
 // Build global mesh
 this->build_global_mesh();
  
 // Setup equation numbering scheme
 cout <<"Number of equations: " << this->assign_eqn_numbers() << std::endl;
 
} // end_of_constructor

Problem setup

During the problem setup the position of all boundary nodes in the pseudo-elastic fluid mesh, apart from those on the bubble boundary, are pinned.

//==start_of_complete_problem_setup=======================================
/// Set boundary conditions and complete the build of all elements
//========================================================================
template<class ELEMENT>
void BubbleInChannelProblem<ELEMENT>::complete_problem_setup()
{      
 // Map to record if a given boundary is on a bubble or not
 map<unsigned,bool> is_on_bubble_bound;
 
 // Loop over the bubbles 
 unsigned nbubble=Bubble_polygon_pt.size();
 for(unsigned ibubble=0;ibubble<nbubble;ibubble++)
  {
   // Get the vector all boundary IDs associated with the polylines that
   // make up the closed polygon
   Vector<unsigned> bubble_bound_id=this->Bubble_polygon_pt[ibubble]->
    polygon_boundary_id();
   
   // Get the number of boundary
   unsigned nbound=bubble_bound_id.size();
   
   // Fill in the map
   for(unsigned ibound=0;ibound<nbound;ibound++)
    {
     // This boundary...
     unsigned bound_id=bubble_bound_id[ibound];
     
     // ...is on the bubble
     is_on_bubble_bound[bound_id]=true;
    }
  } // points on bubble boundary located

We pin both velocity components on the inflow, top and bottom boundaries and the vertical velocity component at the outflow.

 // Re-set the boundary conditions for fluid problem: All nodes are
 // free by default -- just pin the ones that have Dirichlet conditions
 // here. 
 unsigned nbound=Fluid_mesh_pt->nboundary();
 for(unsigned ibound=0;ibound<nbound;ibound++)
  {
   unsigned num_nod=Fluid_mesh_pt->nboundary_node(ibound);
   for (unsigned inod=0;inod<num_nod;inod++)
    {
     // Get node
     Node* nod_pt=Fluid_mesh_pt->boundary_node_pt(ibound,inod);
     
     //Pin both velocities on inflow (0) and side boundaries (1 and 3)
     if((ibound==0) || (ibound==1) || (ibound==3))
      {
       nod_pt->pin(0);
       nod_pt->pin(1);
      }
     
     //If it's the outflow pin only the vertical velocity
     if(ibound==2) {nod_pt->pin(1);}
     
     // Pin pseudo-solid positions apart from bubble boundary which
     // we allow to move
     SolidNode* solid_node_pt = dynamic_cast<SolidNode*>(nod_pt);
     if(is_on_bubble_bound[ibound])
      {
       solid_node_pt->unpin_position(0);
       solid_node_pt->unpin_position(1);
      }
     else
      {
       solid_node_pt->pin_position(0);
       solid_node_pt->pin_position(1);
      }
    }
  } // end loop over boundaries

Next, the bulk elements are made fully functional. For every element the pointers to the time, Reynolds number, Womersley number and the constitutive law for the mesh deformation are set.

 // Complete the build of all elements so they are fully functional
 // Remember that adaptation for triangle meshes involves a complete
 // regneration of the mesh (rather than splitting as in tree-based
 // meshes where such parameters can be passed down from the father
 // element!)
 unsigned n_element = Fluid_mesh_pt->nelement();
 for(unsigned e=0;e<n_element;e++)
  {
   // Upcast from GeneralisedElement to the present element
   ELEMENT* el_pt = dynamic_cast<ELEMENT*>(Fluid_mesh_pt->element_pt(e));
   
   // Set the Reynolds number
   el_pt->re_pt() = &Problem_Parameter::Re;
   
   // Set the Womersley number (same as Re since St=1)
   el_pt->re_st_pt() = &Problem_Parameter::Re;
   
   // Set the constitutive law for pseudo-elastic mesh deformation
   el_pt->constitutive_law_pt()=Problem_Parameter::Constitutive_law_pt;
  }

Finally, we (re-)assign the velocity boundary values by imposing no slip on the channel walls, parallel outflow, and a Poiseuille profile at the inlet.

 // Re-apply boundary values on Dirichlet boundary conditions 
 // (Boundary conditions are ignored when the solution is transferred
 // from the old to the new mesh by projection; this leads to a slight
 // change in the boundary values (which are, of course, never changed,
 // unlike the actual unknowns for which the projected values only
 // serve as an initial guess)
 
 // Set velocity and history values of velocity on walls
 nbound=this->Fluid_mesh_pt->nboundary();
 for(unsigned ibound=0;ibound<nbound;++ibound)
  {
   if ((ibound==Upper_wall_boundary_id)||
       (ibound==Bottom_wall_boundary_id)||
       (ibound==Outflow_boundary_id)||
       (ibound==Inflow_boundary_id))
    {
     // Loop over nodes on this boundary
     unsigned num_nod=this->Fluid_mesh_pt->nboundary_node(ibound);
     for (unsigned inod=0;inod<num_nod;inod++)
      {
       // Get node
       Node* nod_pt=this->Fluid_mesh_pt->boundary_node_pt(ibound,inod);
       
       // Get number of previous (history) values
       unsigned n_prev=nod_pt->time_stepper_pt()->nprev_values();
       
       // Velocity is and was zero at all previous times
       for (unsigned t=0;t<=n_prev;t++)
        {
         if (ibound!=Inflow_boundary_id)
          {
           // Parallel outflow
           if (ibound!=Outflow_boundary_id)
            {
             nod_pt->set_value(t,0,0.0); 
            }
           nod_pt->set_value(t,1,0.0);
          }
         
         // Nodes have always been there...
         nod_pt->x(t,0)=nod_pt->x(0,0);
         nod_pt->x(t,1)=nod_pt->x(0,1);
        }
      }
    }
  }
 
 // Re-assign prescribed inflow velocity at inlet
 unsigned num_nod=this->Fluid_mesh_pt->nboundary_node(Inflow_boundary_id);
 for (unsigned inod=0;inod<num_nod;inod++)
  {
   // Get node
   Node* nod_pt=this->Fluid_mesh_pt->boundary_node_pt(Inflow_boundary_id,
                                                      inod);
   //Now set the boundary velocity
   double y = nod_pt->x(1); 
   nod_pt->set_value(0,Problem_Parameter::Inflow_veloc_magnitude*y*(1-y));
  }
 
} // end of complete_problem_setup

Generation of face elements

As usual we impose the kinematic and dynamic boundary condition at the free surface by attaching FaceElements to the relevant boundaries of the bulk elements. We specify pointers to the Capillary number and the bubble pressure $p_{bubble}$ . The pointer to the Strouhal number does not need to be set, since it already defaults to a value of 1.0.

//============start_of_create_free_surface_elements======================
/// Create elements that impose the kinematic and dynamic bcs
/// for the pseudo-solid fluid mesh
//=======================================================================
template<class ELEMENT>
void BubbleInChannelProblem<ELEMENT>::create_free_surface_elements()
{ 
 
 // Volume constraint element stores the Data item that stores
 // the bubble pressure that is adjusted/traded to allow for
 // volume conservation. Which value is the pressure stored in?
 unsigned p_traded_index=Vol_constraint_el_pt->index_of_traded_pressure();
 
 //Loop over the free surface boundaries
 unsigned nb=Fluid_mesh_pt->nboundary();
 for(unsigned b=First_bubble_boundary_id;b<nb;b++)
  {
   // How many bulk fluid elements are adjacent to boundary b?
   unsigned n_element = Fluid_mesh_pt->nboundary_element(b);
   
   // Loop over the bulk fluid elements adjacent to boundary b?
   for(unsigned e=0;e<n_element;e++)
    {
     // Get pointer to the bulk fluid element that is 
     // adjacent to boundary b
     ELEMENT* bulk_elem_pt = dynamic_cast<ELEMENT*>(
      Fluid_mesh_pt->boundary_element_pt(b,e));
     
     //Find the index of the face of element e along boundary b
     int face_index = Fluid_mesh_pt->face_index_at_boundary(b,e);
     
     // Create new element
     ElasticLineFluidInterfaceElement<ELEMENT>* el_pt =
      new ElasticLineFluidInterfaceElement<ELEMENT>(
       bulk_elem_pt,face_index);   
     
     // Add it to the mesh
     Free_surface_mesh_pt->add_element_pt(el_pt);
     
     //Add the appropriate boundary number
     el_pt->set_boundary_number_in_bulk_mesh(b);
     
     //Specify the capillary number
     el_pt->ca_pt() = &Problem_Parameter::Ca;
 
     // Specify the bubble pressure (pointer to Data object and 
     // index of value within that Data object that corresponds
     // to the traded pressure
     el_pt->set_external_pressure_data(
      Vol_constraint_el_pt->p_traded_data_pt(),p_traded_index); 
    } 
  }
}
// end of create_free_surface_elements

The volume constraint elements are created in a similar way. Recall that the LineVolumeConstraintBoundingSolidElements compute the line integrals in equation (10) while the VolumeConstraintElement adds $V_{bubble}$ to this equation.

//============start_of_create_volume_constraint_elements=================
/// Create elements that impose volume constraint on the bubble
//=======================================================================
template<class ELEMENT>
void BubbleInChannelProblem<ELEMENT>::create_volume_constraint_elements()
{ 
 
 // Add volume constraint element to the mesh
 Volume_constraint_mesh_pt->add_element_pt(Vol_constraint_el_pt);
 
 //Loop over the free surface boundaries
 unsigned nb=Fluid_mesh_pt->nboundary();
 for(unsigned b=First_bubble_boundary_id;b<nb;b++)
  {
   // How many bulk fluid elements are adjacent to boundary b?
   unsigned n_element = Fluid_mesh_pt->nboundary_element(b);
   
   // Loop over the bulk fluid elements adjacent to boundary b?
   for(unsigned e=0;e<n_element;e++)
    {
     // Get pointer to the bulk fluid element that is 
     // adjacent to boundary b
     ELEMENT* bulk_elem_pt = dynamic_cast<ELEMENT*>(
      Fluid_mesh_pt->boundary_element_pt(b,e));
     
     //Find the index of the face of element e along boundary b
     int face_index = Fluid_mesh_pt->face_index_at_boundary(b,e);
     
     // Create new element
     ElasticLineVolumeConstraintBoundingElement<ELEMENT>* el_pt =
      new ElasticLineVolumeConstraintBoundingElement<ELEMENT>(
       bulk_elem_pt,face_index);   
     
     //Set the "master" volume constraint element
     el_pt->set_volume_constraint_element(Vol_constraint_el_pt);
 
     // Add it to the mesh
     Volume_constraint_mesh_pt->add_element_pt(el_pt);     
    } 
  }
}
// end of create_volume_constraint_elements

Post-processing

This member function documents the computed solution after every Newton solve.

//==start_of_doc_solution=================================================
/// Doc the solution
//========================================================================
template<class ELEMENT>
void BubbleInChannelProblem<ELEMENT>::doc_solution(const std::string& comment)
{ 
 oomph_info << "Docing step: " << Problem_Parameter::Doc_info.number()
            << std::endl;
 
 ofstream some_file;
 char filename[100];
 sprintf(filename,"%s/soln%i.dat",
         Problem_Parameter::Doc_info.directory().c_str(),
         Problem_Parameter::Doc_info.number());
 
 // Number of plot points
 unsigned npts;
 npts=5; 
 
 // Compute errors and assign to each element for plotting
 double max_err;
 double min_err;
 compute_error_estimate(max_err,min_err);
 
 // Assemble square of L2 norm 
 double square_of_l2_norm=0.0;
 unsigned nel=Fluid_mesh_pt->nelement();
 for (unsigned e=0;e<nel;e++)
  {
   square_of_l2_norm+=
    dynamic_cast<ELEMENT*>(this->Fluid_mesh_pt->element_pt(e))->
    square_of_l2_norm();
  }
 Problem_Parameter::Norm_file << sqrt(square_of_l2_norm) << std::endl;
 
 
 some_file.open(filename);
 some_file << dynamic_cast<ELEMENT*>(this->Fluid_mesh_pt->element_pt(0))
  ->variable_identifier();
 this->Fluid_mesh_pt->output(some_file,npts);   
 some_file << "TEXT X = 25, Y = 78, CS=FRAME T = \"Global Step " 
           << Problem_Parameter::Doc_info.number() << "  " 
           << comment << "\"\n";
 some_file.close();
 
 
 
 // Output boundaries
 sprintf(filename,"%s/boundaries%i.dat",
         Problem_Parameter::Doc_info.directory().c_str(),
         Problem_Parameter::Doc_info.number());
 some_file.open(filename);
 this->Fluid_mesh_pt->output_boundaries(some_file);
 some_file.close();
 
 // Get max/min area
 double max_area;
 double min_area;
 Fluid_mesh_pt->max_and_min_element_size(max_area, min_area);
 
 // Get total volume enclosed by face elements (ignore first one)
 double vol=0.0;
 vol=Problem_Parameter::Volume;
 
 // Write trace file
 Problem_Parameter::Trace_file 
  << this->time_pt()->time() << " " 
  << Fluid_mesh_pt->nelement() << " "
  << max_area << " "
  << min_area << " "
  << max_err << " "
  << min_err << " "
  << sqrt(square_of_l2_norm) << " "
  << vol << " "
  << std::endl;
 
 // Increment the doc_info number
 Problem_Parameter::Doc_info.number()++;
 
} //end_of_doc_solution

Comments and Exercises

Mesh adaptation for problems with 'closed' free boundaries

We described in another tutorial how oomph-lib employs a two-stage process for the (re-)generation of unstructured meshes in domains whose curvilinear boundaries are represented by GeomObjects: we initially sample the GeomObject at a user-specified number of points (equally spaced along the relevant section of the GeomObject) to create the vertices for an initial polygonal representation of the curvilinear boundary. This polygonal boundary representation is used to generate a new mesh with Triangle. The nodes on the domain boundaries are then "snapped" onto the curvilinear boundaries where required.

In principle, the same methodology can be (and is) employed for the mesh regeneration in free-surface problems. However, in a free-surface problem the curvilinear boundary evolves freely as part of the solution and is therefore not described by a user-specified GeomObject. When re-generating the mesh we therefore create a temporary GeomObject by attaching FaceElements to the relevant mesh boundaries of the existing mesh. We then use the vertices of the face elements to create a polyline representation of the boundary. This is illustrated in the figure below which shows part of the original mesh (the nodes and triangular elements adjacent to the boundary) in black. The blue lines represent the FaceElements that are erected on the current curvilinear domain boundary (as defined by the boundaries of the "bulk" elements). The vertices of these FaceElements (red hollow circles) provide the vertices for the polyline representation of the boundary (red line).

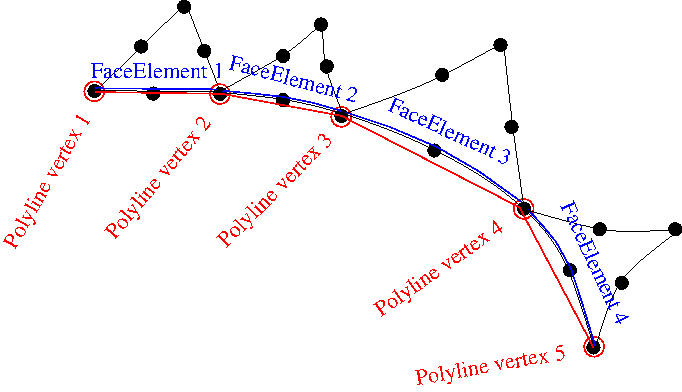
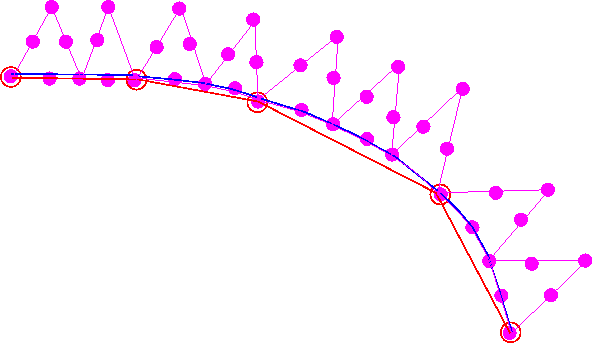
Sketch illustrating the generation of a polyline along the curvilinear domain boundary.

Using this polyline representation of the boundary, a new mesh is built using Triangle. Depending on the target areas specified by the spatial error estimator, Triangle may erect multiple elements along each polyline segment. For instance in the figure below three elements have been created along the polyline segment created from FaceElement 3 in the original mesh.

Sketch showing the new mesh generated by Triangle, using (i) the polygonal representation of the boundary and (ii) the area targets provided by the spatial error estimator.

Next, the boundary coordinates are set up and the nodes are snapped onto the curvilinear boundary that is still defined by the FaceElements that were attached to the original mesh, as shown below.

Sketch showing the mesh following the snapping of nodes to the curvilinear boundary.

IMPORTANT:
Note that the initial shape of moving free boundaries must not be described by TriangleMeshCurviLines. While the use of TriangleMeshCurviLines would ensure that the nodes are initially located exactly on the curvilinear boundary described by the associated GeomObject without having to "snap" them to their desired position, a problem arises when the mesh is adapted. When this happens, nodes on curvilinear boundaries that are described by TriangleMeshCurviLines are placed on the (presumably unchanged) geometry defined by the associated GeomObject rather than being placed on the deformed boundary as described above – the free surface therefore keeps jumping back to its initial position whenever the mesh is adapted which is unlikely to be desired!

Modifications to the basic mesh re-generation procedure

The procedure described above is very robust and works satisfactorily in the example problem discussed in this tutorial. Below we discuss a a few optional modifications to the mesh regeneration procedure that are helpful to deal with complications that can arise in certain circumstances:

Unrefinement of polylines

As discussed above, Triangle generates a new mesh, based on (i) the polygonal representation of the boundary and (ii) the area targets provided by the spatial error estimator for the bulk elements. The polygonal boundary representation defines the minimum number of bulk elements that are generated next to the boundary – we showed above how multiple elements can be erected on a given boundary segment. However, since Triangle never merges any boundary segments this procedure can result in unnecessarily fine meshes near the boundary: once the bulk mesh has been refined to a certain level, the polygonal boundary representation cannot be coarsened, even if the spatial error estimator would allow much larger elements to be created at a later stage of the simulation.

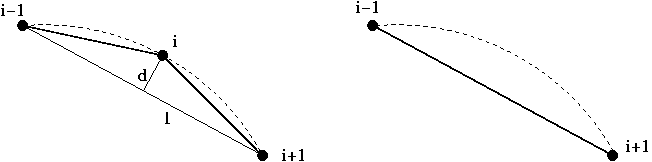
We therefore provide the option to coarsen the polygonal boundary representation following its creation from the FaceElements that are attached to the current mesh. This is done by assessing if the (geometrical) boundary representation is unnecessarily fine, judged by how close any three adjacent vertices are to a straight line. This is illustrated in the sketch below: To assess if the middle vertex can be deleted, we determine the height of a circular segment connecting the three vertices. If the ratio of this height, , to the distance between the two outer vertices is less than a user-defined tolerance (i.e. if the local curvature is so small that the middle vertex is not required to represent the boundary sufficiently accurately), the middle vertex is deleted.

Sketch illustrating the criterion for the unrefinement of polylines.

The tolerance for the unrefinement of polygons is set by the function

TriangleMesh::set_polyline_unrefinement_tolerance(...)

By default we allow polyline unrefinement (with a default tolerance of 0.04). Polyline unrefinement can be disabled by calling

TriangleMesh::disable_polyline_unrefinement()

where TriangleMesh is a base for the TriangleMeshClosedCurve class.

Refinement of polylines

It is also possible that the free surface deforms in such a way that the polyline representation of the domain boundary becomes too inaccurate, e.g. because the representation of the solution only requires fairly large elements. Even though large elements may be sufficient to represent the solution, the mesh-regeneration tends to fail when "snapping" the nodes onto the highly-curved curvilinear boundary (typically because elements near the boundary become highly distorted or even inverted).

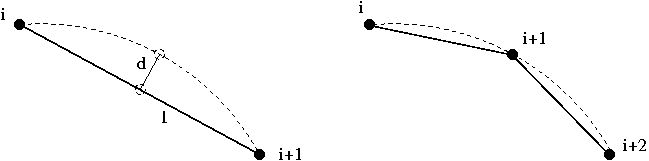
We therefore provide the option to refine the polygonal representation of the boundary employing a criterion similar to the one used for unrefinement discussed above. To assess the need for a boundary refinement we consider each boundary segment and compute the distance from segment's mid-point to its counterpart on the curvilinear boundary. If the ratio of the distance between these points, , to the length of the segment connecting the vertices, , is larger than a user-specifiable tolerance, the point on the curvilinear boundary becomes an additional vertex of the polyline and the original segment is split into two as illustrated in the figure below:

Sketch illustrating the criterion for the refinement of polylines.

The tolerance for the refinement of polygons is set by the function

TriangleMesh::set_polyline_refinement_tolerance(...)

By default we allow polyline refinement (with a default tolerance of 0.08). Polyline refinement can be disabled by calling

TriangleMesh::disable_polyline_refinement()

Redistribution of segments between polylines

The kinematic boundary condition (5) determines only the normal displacement of the boundary, hence the tangential displacement of nodes on the boundary is not controlled directly. It is therefore possible that nodes move along the perimeter of the curvilinear boundary and, as a result, one polyline may become much shorter than the others, as illustrated in the transition from a) to b) in the figure below. This is clearly undesirable and can be avoided by redistributing the vertices/segment between the polygon's constituent polylines such that each polyline spans an approximately equal fraction of the polygon's overall perimeter. This process is illustrated in b) and c) in the figure below. Note that the redistribution of segments does not change the shape of the polygonal boundary but merely the way in which it is represented in terms of polylines.

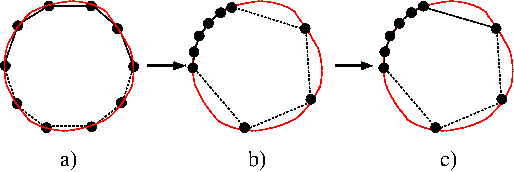
Sketch illustrating the optional redistribution of polyline segments.

We provide the option to perform this step immediately after the generation of the updated polyline representation for the curvilinear boundary (and before the boundary refinement/unrefinement discussed above). Given that each polyline represents a distinct mesh boundary, the redistribution of segments between different polylines moves nodes from one boundary to another and, in general, this is clearly undesirable. Therefore, the redistribution of segments is is deactivated by default and must be activated by calling the function

TriangleMeshPolygon::enable_redistribution_of_segments_between_polylines()

Note that the redistribution of segments is not possible/sensible for TriangleMeshClosedCurve formed by TriangleMeshCurviLines since such boundaries are associated with a specific, continuous GeomObject with specific start/end coordinates.

Exercises

As discussed above, we start the simulation by performing an initial steady Newton solve during which we deform the polygonal boundary that represents the air-liquid interface into its static equilibrium shape – a circle enclosing the required volume. This may seem like a rather costly way of creating a circular interface. Why not simply move the nodes on that boundary manually to their "correct" positions by adjusting their radial positions after returning from the mesh constructor? To explore this question, snap the required nodes manually onto the circular boundary and call the steady Newton solver. Why is the initial residual not equal to zero, even though we have manually assigned the correct solution as an initial guess?
Comment out create_volume_constraint_elements() and delete_volume_constraint_elements() throughout the code and explain what happens.
Experiment with the refinement/unrefinement of polylines and explore the option to re-distribute segments between the polylines that define the boundaries of the bubble. Specifically, change the initial polygonal representation the bubble surface such that the first TriangleMeshPolyLine only represents 1/4 of the perimeter while the second one represents the remaining 3/4. Confirm that, following the mesh adaptation, the bubble boundaries are adjusted such that each boundary occupies approximately 1/2 of the bubble surface when the redistribution of polylines is enabled.

Source files for this tutorial

The source files for this tutorial are located in the directory: demo_drivers/navier_stokes/unstructured_adaptive_fs/
The driver code is: demo_drivers/navier_stokes/unstructured_adaptive_fs/adaptive_bubble_in_channel.cc .

PDF file

A pdf version of this document is available.