Thermoelasticity: Combining the Heat equation and non-linear Solid Mechanics

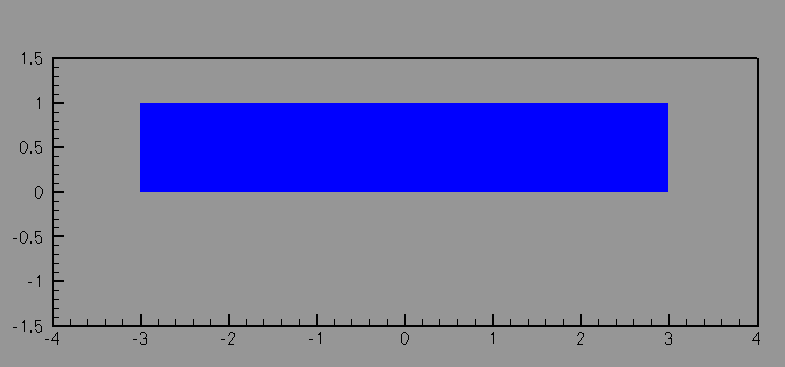
Undeformed configuration of an elastic block.

We consider the uniform steady thermal expansion of an elastic body that is differentially heated. The top surface is heated and the bottom surface is maintained at the reference temperature, which leads to a uniform temperature gradient throughout the material. The material expands more near the upper surface than near the lower surface, deforming the initially rectangular block into an curved configuration.

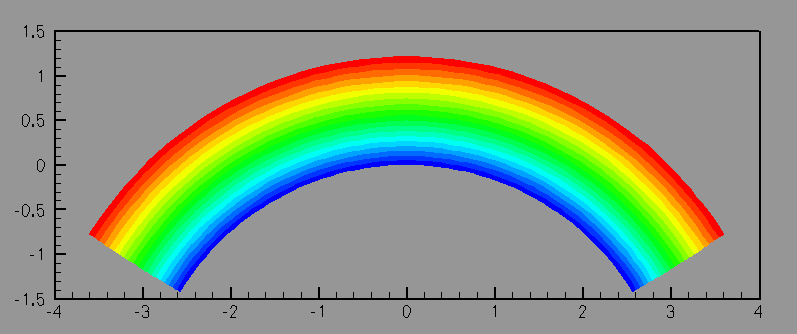
Deformed elastica when the top surface is heated and the lower surface is maintained at the reference temperature. The contours indicate the temperature of the body.

---

---

The driver code

The driver code for this example is given below:

//LIC// ====================================================================
//LIC// This file forms part of oomph-lib, the object-oriented, 
//LIC// multi-physics finite-element library, available 
//LIC// at http://www.oomph-lib.org.
//LIC// 
//LIC// Copyright (C) 2006-2024 Matthias Heil and Andrew Hazel
//LIC// 
//LIC// This library is free software; you can redistribute it and/or
//LIC// modify it under the terms of the GNU Lesser General Public
//LIC// License as published by the Free Software Foundation; either
//LIC// version 2.1 of the License, or (at your option) any later version.
//LIC// 
//LIC// This library is distributed in the hope that it will be useful,
//LIC// but WITHOUT ANY WARRANTY; without even the implied warranty of
//LIC// MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the GNU
//LIC// Lesser General Public License for more details.
//LIC// 
//LIC// You should have received a copy of the GNU Lesser General Public
//LIC// License along with this library; if not, write to the Free Software
//LIC// Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA
//LIC// 02110-1301  USA.
//LIC// 
//LIC// The authors may be contacted at oomph-lib@maths.man.ac.uk.
//LIC// 
//LIC//====================================================================
//Driver for a multi-physics problem that couples the 
//unsteady heat equation to the equations of large-displacement solid
//mechanics
 
//Oomph-lib headers, we require the generic, unsteady heat
//and and elements.
#include "generic.h"
#include "solid.h"
#include "unsteady_heat.h"
 
// The mesh is our standard rectangular quadmesh
#include "meshes/rectangular_quadmesh.h"
 
// Use the oomph and std namespaces 
using namespace oomph;
using namespace std;
 
 
 
//=====================================================================
/// A class that solves the equations of steady thermoelasticity by 
/// combining the UnsteadyHeat and PVD equations into a single element.
/// A temperature-dependent growth term is added to the PVD equations by
/// overloading the member function get_istotropic_growth()
//======================class definition==============================
template<unsigned DIM>
class QThermalPVDElement : public virtual QPVDElement<DIM,3>,
                           public virtual QUnsteadyHeatElement<DIM,3>
{
private:
 
 /// Pointer to a private data member, the thermal expansion coefficient
 double* Alpha_pt;
 
 /// The static default value of Alpha
 static double Default_Physical_Constant_Value;
 
public:
 /// Constructor: call the underlying constructors and 
 /// initialise the pointer to Alpha to point
 /// to the default value of 1.0.
 QThermalPVDElement() : QPVDElement<DIM,3>(),
                        QUnsteadyHeatElement<DIM,3>() 
  {
   Alpha_pt = &Default_Physical_Constant_Value;
  }
 
 /// The required number of values stored at the nodes is the sum of the
 /// required values of the two single-physics elements. Note that this step is
 /// generic for any multi-physics element of this type.
 unsigned required_nvalue(const unsigned &n) const
  {return (QUnsteadyHeatElement<DIM,3>::required_nvalue(n) +
           QPVDElement<DIM,3>::required_nvalue(n));}
 
 /// Access function for the thermal expansion coefficient (const version)
 const double &alpha() const {return *Alpha_pt;}
 
 /// Access function for the pointer to the thermal expansion coefficientr
 double* &alpha_pt() {return Alpha_pt;}
  
 ///  Overload the standard output function with the broken default
 void output(ostream &outfile) {FiniteElement::output(outfile);}
 
 /// Output function:  
 ///  Output x, y, u, v, p, theta at Nplot^DIM plot points
 // Start of output function
 void output(ostream &outfile, const unsigned &nplot)
  {
   //vector of local coordinates
   Vector<double> s(DIM);
   Vector<double> xi(DIM);
   
   // Tecplot header info
   outfile << this->tecplot_zone_string(nplot);
   
   // Loop over plot points
   unsigned num_plot_points=this->nplot_points(nplot);
   for (unsigned iplot=0;iplot<num_plot_points;iplot++)
    {
     // Get local coordinates of plot point
     this->get_s_plot(iplot,nplot,s);
     
     // Get the Lagrangian coordinate
     this->interpolated_xi(s,xi);
 
     // Output the position of the plot point
     for(unsigned i=0;i<DIM;i++) 
      {outfile << this->interpolated_x(s,i) << " ";}
 
     // Output the temperature (the advected variable) at the plot point
     outfile << this->interpolated_u_ust_heat(s) << std::endl;   
    }
   outfile << std::endl;
   
   // Write tecplot footer (e.g. FE connectivity lists)
   this->write_tecplot_zone_footer(outfile,nplot);
  } //End of output function
 
 /// C-style output function: Broken default
 void output(FILE* file_pt)
  {FiniteElement::output(file_pt);}
 
 ///  C-style output function: Broken default
 void output(FILE* file_pt, const unsigned &n_plot)
  {FiniteElement::output(file_pt,n_plot);}
 
 /// Output function for an exact solution: Broken default
 void output_fct(ostream &outfile, const unsigned &Nplot,
                 FiniteElement::SteadyExactSolutionFctPt 
                 exact_soln_pt)
  {FiniteElement::output_fct(outfile,Nplot,exact_soln_pt);}
 
 
 /// Output function for a time-dependent exact solution:
 /// Broken default.
 void output_fct(ostream &outfile, const unsigned &Nplot,
                 const double& time,
                 FiniteElement::UnsteadyExactSolutionFctPt 
                 exact_soln_pt)
  {
   FiniteElement::
    output_fct(outfile,Nplot,time,exact_soln_pt);
  }
  
 /// Compute norm of solution: use the version in the unsteady heat
 /// class 
 void compute_norm(double& el_norm)
 {
  QUnsteadyHeatElement<DIM,3>::compute_norm(el_norm);
 }
 
 /// Validate against exact solution at given time
 /// Solution is provided via function pointer.
 /// Plot at a given number of plot points and compute L2 error
 /// and L2 norm of velocity solution over element
 /// Call the broken default
 void compute_error(ostream &outfile,
                    FiniteElement::UnsteadyExactSolutionFctPt exact_soln_pt,
                    const double& time,
                    double& error, double& norm)
  {FiniteElement::compute_error(outfile,exact_soln_pt,
                                time,error,norm);}
 
 /// Validate against exact solution.
 /// Solution is provided via function pointer.
 /// Plot at a given number of plot points and compute L2 error
 /// and L2 norm of velocity solution over element
 /// Call the broken default
 void compute_error(ostream &outfile,
                    FiniteElement::SteadyExactSolutionFctPt exact_soln_pt,
                    double& error, double& norm)
  {FiniteElement::compute_error(outfile,exact_soln_pt,error,norm);}
 
 /// Overload the growth function in the advection-diffusion equations.
 /// to be temperature-dependent.
 void get_isotropic_growth(const unsigned& ipt, const Vector<double> &s, 
                           const Vector<double>& xi, double &gamma) const
 {
  //The growth is the undeformed coefficient plus linear thermal
  //expansion
  gamma = 1.0 + (*Alpha_pt)*this->interpolated_u_ust_heat(s);
 }
 
 /// Calculate the contribution to the residual vector.
 /// We assume that the vector has been initialised to zero
 /// before this function is called.
 void fill_in_contribution_to_residuals(Vector<double> &residuals)
  {
   //Call the residuals of the advection-diffusion eqautions
   UnsteadyHeatEquations<DIM>::
    fill_in_contribution_to_residuals(residuals);
   //Call the residuals of the Navier-Stokes equations
   PVDEquations<DIM>::
    fill_in_contribution_to_residuals(residuals);
  }
 
 /// Compute the element's residual Vector and the jacobian matrix
 /// We assume that the residuals vector and jacobian matrix have been
 /// initialised to zero before calling this function
 void fill_in_contribution_to_jacobian(Vector<double> &residuals,
                                       DenseMatrix<double> &jacobian)
  {
   //Just call standard finite difference for a SolidFiniteElement so 
   //that variations in the nodal positions are taken into account
   SolidFiniteElement::fill_in_contribution_to_jacobian(residuals,jacobian);
  }
 
};
 
//=========================================================================
/// Set the default physical value to be one
//=========================================================================
template<>
double QThermalPVDElement<2>::Default_Physical_Constant_Value=1.0;
 
//======start_of_namespace============================================
/// Namespace for the physical parameters in the problem
//====================================================================
namespace Global_Physical_Variables
{
 /// Thermal expansion coefficient 
 double Alpha=0.0;
 
 /// Young's modulus for solid mechanics
 double E = 1.0; // ADJUST 
 
 /// Poisson ratio for solid mechanics
 double Nu = 0.3; // ADJUST
 
 /// We need a constitutive law for the solid mechanics
 ConstitutiveLaw* Constitutive_law_pt;
 
} // end_of_namespace
 
/// ///////////////////////////////////////////////////////////////////
/// ///////////////////////////////////////////////////////////////////
/// ///////////////////////////////////////////////////////////////////
 
//====== start_of_problem_class=======================================
/// 2D Thermoelasticity problem on rectangular domain, discretised 
/// with refineable elements. The specific type
/// of element is specified via the template parameter.
//====================================================================
template<class ELEMENT> 
class ThermalProblem : public Problem
{
 
public:
 
 /// Constructor
 ThermalProblem();
 
 /// Destructor. Empty
 ~ThermalProblem() {}
 
 /// Update the problem specs before solve (empty)
 void actions_before_newton_solve() {}
 
 /// Update the problem after solve (empty)
 void actions_after_newton_solve(){}
 
 /// Actions before adapt:(empty)
 void actions_before_adapt(){}
 
 /// Doc the solution.
 void doc_solution();
 
 /// Overloaded version of the problem's access function to 
 /// the mesh. Recasts the pointer to the base Mesh object to 
 /// the actual mesh type.
 ElasticRectangularQuadMesh<ELEMENT>* mesh_pt() 
  {
   return dynamic_cast<ElasticRectangularQuadMesh<ELEMENT>*>(
    Problem::mesh_pt());
  }
 
private:
 
 /// DocInfo object
 DocInfo Doc_info;
 
}; // end of problem class
 
//========================================================================
/// Constructor for Convection problem
//========================================================================
template<class ELEMENT>
ThermalProblem<ELEMENT>::ThermalProblem()
{
 // Set output directory
 Doc_info.set_directory("RESLT");
 
 // # of elements in x-direction
 unsigned n_x=8;
 
 // # of elements in y-direction
 unsigned n_y=8;
 
 // Domain length in x-direction
 double l_x=3.0;
 
 // Domain length in y-direction
 double l_y=1.0;
 
 // Build a standard rectangular quadmesh
 Problem::mesh_pt() = 
  new ElasticRectangularQuadMesh<ELEMENT>(n_x,n_y,l_x,l_y);
 
 // Set the boundary conditions for this problem: All nodes are
 // free by default -- only need to pin the ones that have Dirichlet 
 // conditions here
 {
  //The temperature is prescribed on the lower boundary
  unsigned n_boundary_node = mesh_pt()->nboundary_node(0);
  for(unsigned n=0;n<n_boundary_node;n++)
   {
    //Get the pointer to the node
    Node* nod_pt = mesh_pt()->boundary_node_pt(0,n);
    //Pin the temperature at the node 
    nod_pt->pin(0);
    //Set the temperature to 0.0 (cooled)
    nod_pt->set_value(0,0.0);
   }
  
  //The temperature is prescribed on the upper boundary
  n_boundary_node = mesh_pt()->nboundary_node(2);
  for(unsigned n=0;n<n_boundary_node;n++)
   {
    Node* nod_pt = mesh_pt()->boundary_node_pt(2,n);
    //Pin the temperature at the node
    nod_pt->pin(0);
    //Set the temperature to 1.0 (heated)
    nod_pt->set_value(0,1.0);
   }
  
  //The horizontal-position is fixed on the vertical boundary (symmetry)
  n_boundary_node = mesh_pt()->nboundary_node(1);
  for(unsigned n=0;n<n_boundary_node;n++)
   {
    static_cast<SolidNode*>(mesh_pt()->boundary_node_pt(1,n))->pin_position(0);
   }
  
  //We need to completely fix the lower-right corner of the block to 
  //prevent vertical rigid-body motions
  static_cast<SolidNode*>(mesh_pt()->boundary_node_pt(1,0))->pin_position(1);
 }
 
 // Complete the build of all elements so they are fully functional 
 
 // Loop over the elements to set up element-specific 
 // things that cannot be handled by the (argument-free!) ELEMENT 
 // constructor.
 unsigned n_element = mesh_pt()->nelement();
 for(unsigned int i=0;i<n_element;i++)
  {
   // Upcast from GeneralsedElement to the present element
   ELEMENT *el_pt = dynamic_cast<ELEMENT*>(mesh_pt()->element_pt(i));
 
   // Set the coefficient of thermal expansion
   el_pt->alpha_pt() = &Global_Physical_Variables::Alpha;
 
   // Set a constitutive law
   el_pt->constitutive_law_pt() = 
    Global_Physical_Variables::Constitutive_law_pt;
  }
 
 // Setup equation numbering scheme
 cout <<"Number of equations: " << assign_eqn_numbers() << endl; 
 
} // end of constructor
 
 
//========================================================================
/// Doc the solution
//========================================================================
template<class ELEMENT>
void ThermalProblem<ELEMENT>::doc_solution()
{ 
 //Declare an output stream and filename
 ofstream some_file;
 char filename[100];
 
 // Number of plot points: npts x npts
 unsigned npts=5;
 
 // Output solution 
 //-----------------
 sprintf(filename,"%s/soln%i.dat",Doc_info.directory().c_str(),
         Doc_info.number());
 some_file.open(filename);
 mesh_pt()->output(some_file,npts);
 some_file.close();
 
 Doc_info.number()++;
} // end of doc
 
 
//=====================================================================
/// Driver code for 2D Thermoelasticity problem
//====================================================================
int main(int argc, char **argv)
{
 
 // "Big G" Linear constitutive equations:
 Global_Physical_Variables::Constitutive_law_pt = 
  new GeneralisedHookean(&Global_Physical_Variables::Nu,
                         &Global_Physical_Variables::E);
 
 //Construct our problem
 ThermalProblem<QThermalPVDElement<2> > problem;
 
 //Number of quasi-steady steps
 unsigned n_steps = 11;
 //If we have additional command line arguemnts, take fewer steps
 if(argc > 1) {n_steps = 2;}
 for(unsigned i=0;i<n_steps;i++)
  {
   //Increase the thermal expansion coefficient
   Global_Physical_Variables::Alpha = 0.1*i;
   
   //Perform a single steady newton solve
   problem.newton_solve();
   //Document the solution
   problem.doc_solution();
  }
} // end of main
 
 
 
 
 
 
 
 
 

---

---

Source files for this tutorial

• The source files for this tutorial are located in the directory:
  
  demo_drivers/multi_physics/thermo/
  
• The driver code is:
  
  demo_drivers/multi_physics/thermo/thermo.cc

---

---

PDF file

A pdf version of this document is available.