In this document we discuss the implementation of segregated solution strategies for multi-physics problems, in particular fluid-structure interaction, within oomph-lib. The method illustrated by revisiting the fluid-structure interaction problem of finite-Reynolds-number flow in a 2D collapsible channel; an example discussed in detail in

Heil, M., Hazel, A.L. & Boyle, J. (2008): Solvers for large-displacement fluid-structure interaction problems: Segregated vs. monolithic approaches. Computational Mechanics.

where we compare the relative performance of segregated and monolithic solvers. Since the paper comes to the conclusion that, despite various claims in the literature, segregated solvers are not necessarily more efficient than fully-coupled monolithic schemes (of the type employed in oomph-lib) you should also consult the related tutorial on the monolithic solution of the problem with oomph-lib's FSI preconditioner.

The problem

Flow in a 2D collapsible channel

The figure below shows a sketch of the problem: Flow is driven by a prescribed Poiseuille flow 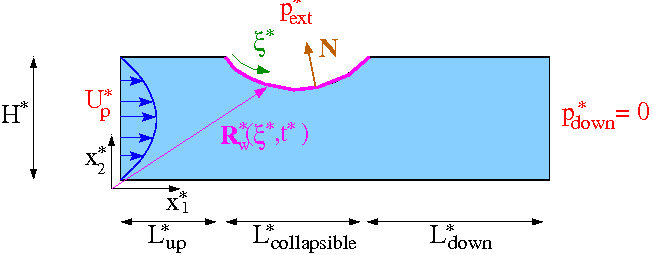$U^{*}_{p}$ through a 2D channel of width and total length $L^*_{total} = L^*_{up} + L^*_{collapsible} + L^*_{down}.$ The upstream and downstream lengths of the channel are rigid, whereas the upper wall in the central section is an elastic membrane whose shape is parametrised by a Lagrangian coordinate, $\xi^*$ , so that the position vector to the moving wall is given by ${\bf R}_w^*(\xi^*,t^*)$ . The wall is loaded by the external pressure $p_{ext}^*$ and by the traction that the viscous fluid exerts on it.

Sketch of the problem.

The non-dimensionalisation and governing equations have already been discussed in the previous (monolithic) example. The problem is not quite the same, however, because the upstream boundary condition is now one of prescribed flow, rather than prescribed pressure:

Prescribed inflow,
${\bf u}(x_1,x_2) = {\bf u}_{p}(x_1,x_2) = 6 \ x_2 \ (1-x_2) \ {\bf e}_1. \ \ \ \ \ \ \ \ \ \ (1)$
at $x_{1}=0$ .

All other boundary conditions remain the same.

Results

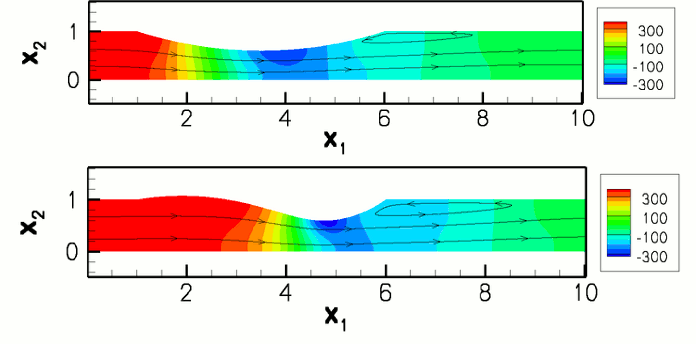
The behaviour of the system under the prescribed-inflow boundary conditions is somewhat different to its behaviour when the pressure drop is prescribed. In the first instance, we consider steady states, in which all time-derivatives are neglected. The figure below shows steady flows at a Reynolds number of and two values of the fluid-structure-interaction parameter, $Q = 10^{-4}$ (upper) and $Q = 10^{-2}$ (lower). For low values of , corresponding to weak fluid-structure interaction, the deformation of the wall is approximately symmetric, being dominated by the external pressure. As increases, the influence of fluid traction can been seen in the asymmetric deformation of the elastic wall. The viscous pressure drop along the tube leads to higher pressure upstream (causing an outward deformation) and lower pressures downstream (causing an inward deflection).

Steady flows at Re=500 and Q=10e-4 (upper), Q=10e-2 (lower).

The overall behaviour of the system can be characterised by steady load-displacement curves in which the vertical position of a control point on the elastic section of the channel wall is plotted as a function of the external pressure.

Load-displacement curve: the vertical position of a control point on the elastic wall (located at 50, 50, 60 and 70 percent of its length for Q = 0, 10e-4, 10e-3 and 10e-2, respectively) as a function of the external pressure.

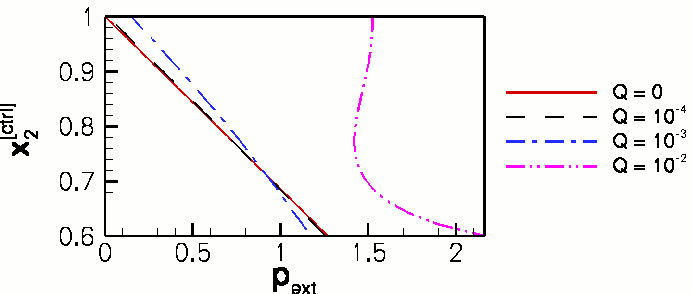
At low , the displacement is directly proportional to the external pressure. As increases the curves shift to the right because a large external pressure is required to keep the wall in its undeformed position;
a consequence of the increased viscous pressure drop and the boundary condition that at the outlet. A second consequence of increasing is that (at finite Reynolds number) a smaller increase in external pressure is required to achieve a given degree of collapse. This is because the Bernoulli effect reduces the fluid pressure in the region that is most strongly collapsed and therefore increases the compressive load on the wall. For $Q = 10^{-2}$ two limit points develop on the load-displacement curve, indicating that the wall "snaps through" into a collapsed buckled configuration when $p_{ext}$ becomes sufficiently large. The appearance of the limit points means that it is no longer possible to perform the steady parameter study by slowly increasing $p_{ext}:$ At sufficiently large values of the displacement of the control point is not a single-valued function of the external pressure $p_{ext}$ . However, the application of "displacement control", described in the tutorial discussing the large-displacement post-buckling of an elastic ring is sufficient to circumvent this difficulty: We treat the external pressure as an unknown and control the channel's collapse by prescribing the vertical position of the control point, $x_2^{[ctrl]}.$ This resolves the problem because the curve $p_{ext}(x_2^{[ctrl]})$ is single-valued, allowing us to perform the parameter study by slowly increasing the wall collapse by reducing $x_2^{[ctrl]}$ , computing the pressure required to achieve this deformation as part of the solution.

Overview: Segregated solution strategies with oomph-lib

The general methodology for setting up fluid-structure-interaction problems is discussed in another tutorial; and we shall assume that the standard monolithic problem has already been written. In the present example, the monolithic problem class FSICollapsibleChannelProblem is specified in the header file fsi_chan_problem.h

Having specified the monolithic (fully-coupled) discretisation, our segregated solution strategy proceeds by alternating between fluid and solid solves: Initially, the degrees of freedom associated with the (pure) solid mechanics problem are "pinned" and the global assembly procedure is modified to omit the corresponding solid elements. The Newton solver will, therefore, solve the fluid equations with a "frozen" wall shape. Next, the degrees of freedom associated with the (pure) fluid mechanics problem are pinned and the original boundary conditions for the solid mechanics problem are re-assigned. The assembly procedure is now modified so that only solid elements contribute to the global system. The Newton solver will then solve for a new wall shape corresponding to the tractions exerted by the given flow field. At this point we allow for under-relaxation, i.e. we provide the option to increment the solid mechanics degrees of freedom by a fraction of the change computed by the Newton solver. These two steps are repeated in a fixed-point iteration which continues until a given convergence criterion is satisfied, or a maximum number of iterations is exceeded. We note that different linear solvers/preconditioners may be specified for solution of the linear systems arising during the Newton iteration for the isolated "fluid" and "solid" problems, allowing the re-use of optimal solution methods for individual sub-problems. This is generally perceived to be one of the key advantages of segregated solvers.

Brief discussion of the implementation

The SegregatableFSIProblem

a. Overall structure

The SegregatableFSIProblem class is used to implement our segregated solution strategy within oomph-lib. The most important problem-specific task is to divide all the problem data into distinct fluid and solid degrees of freedom and to partition the monolithic mesh into a mesh of fluid elements and a mesh of solid elements. The problem-specific partitioning should be implemented in the (pure) virtual member function

/// Identify fluid and solid data
virtual void identify_fluid_and_solid_dofs(Vector<Data*>& fluid_data_pt,
                                           Vector<Data*>& solid_data_pt,
                                           Mesh*& fluid_mesh_pt,
                                           Mesh*& solid_mesh_pt)=0;

which returns vectors of fluid and solid data and the meshes of fluid and solid elements. This virtual function is called within the member function

/// \short Set up segregated solver. The optional boolean argument
/// defaults to true and causes the identify_fluid_and_solid_dofs(...)
/// to be called again. This is required, e.g. if any of the
/// meshes were adapted since the previous call to the segregated solver.
void setup_segregated_solver(const bool &full_setup_of_fluid_and_solid_dofs=true)

which must be called immediately before every segregated solve. The optional boolean flag may be set to false if the solid and fluid meshes have not changed between solves (i.e. if no spatial adaptation was performed since the last call to the segregated solver). The setup_segregated_solver(...) function must still be called, however, in order that data associated with convergence acceleration techniques is reset to its default values.

b. The segregated solvers

The class inherits from the standard Problem class, which provides the standard (monolithic) newton_solve() and related functions. Thus any SegregatedFSIProblem can be solved "monolithically" as normal and, moreover, it is straightforward to ensure that exactly the same system is being solved when comparing monolithic and segregated solutions. The segregated solution strategy is implemented in the analogous member functions:

The equivalent of the monolithic Problem::newton_solve() is
SegregatedFSIProblem::segregated_solve();
The equivalent of the monolithic Problem::steady_newton_solve() is
SegregatedFSIProblem::steady_segregated_solve();
Finally, the equivalent of Problem::unsteady_newton_solve(dt) is
PicardConvergenceData unsteady_segregated_solve(const double &dt);

All three functions return an instance of a PicardConvergenceData object which stores the convergence statistics of the segregated solve.

In addition, the virtual member functions

SegregatedFSIProblem::actions_before_segregated_solve()

SegregatedFSIProblem::actions_after_segregated_solve()

SegregatedFSIProblem::actions_before_segregated_convergence_check()

are provided to allow the user to specify any actions, such as initialisation of counters, mesh updates, output, etc, that should be performed before or after each complete segregated solve. Note that the Problem member functions

Problem::actions_before_newton_solve()

Problem::actions_after_newton_solve()

Problem::actions_before_newton_convergence_check()

are called as usual during the Newton solve of each sub-problem and may be used for fine-grained operations that should be performed before or after each fluid or solid solve. For this purpose, the SegregatedFSIProblem provides a flag, int SegregatedFSIProblem::Solve_type that indicates which (sub-)solve is currently being performed. The flag can take the (enumerated) values SegregatedFSIProblem::Full_solve, SegregatedFSIProblem::Fluid_solve and SegregatedFSIProblem::Solid_solve, allowing the user to perform specific actions during the distinct sub-solves.

c. Choosing the convergence criterion

Other public member functions provided by the SegregatedFSIProblem class are used to specify the convergence criterion for the global fixed-point iteration:

/// Base convergence based on max. global residual

void assess_convergence_based_on_max_global_residual(const double &tol)

/// Base convergence on maximum absolute change of solid degrees of freedom

void assess_convergence_based_on_absolute_solid_change(const double &tol)

/// Base convergence on maximum relative change of solid degrees of freedom

void assess_convergence_based_on_relative_solid_change(const double &tol)

If a tolerance is not specified the default Problem::Newton_solver_tolerance is used.

d. Under-relaxation

Finally, there are several member functions that are used to specify the convergence-acceleration techniques:

Static under-relaxation:

//Use under-relaxation for solid degrees of freedom and specify

//the optional under-relaxation parameter. The default of 1.0

//corresponds to no under-relaxation.

void use_under_relaxation (const double &omega=1.0)

If this function is called, under-relaxation is performed after the solid sub-solve, i.e. each solid degree of freedom, , say is updated via
$s = s_{new} + (1-\omega) (s_{old} - s_{new})$
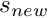where $s_{new}$ is the new value computed by the Newton solver and 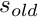$s_{old}$ is its previous value.
Adaptive under-relaxation:

//Boolean flag that controls whether Irons & Tuck extrapolation

//is used to dynamically modify the under-relaxation parameter for

//the under-relaxation of the solid degrees of freedom.

void enable_irons_and_tuck_extrapolation ()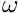

If this function is called (and if under-relaxation is enabled) the under-relaxation parameter $\omega$ is adjusted throughout the fixed-point iteration, using Irons & Tucks convergence acceleration procedure; see Irons, B.M. & Tuck, R.C. "A version of the Aitken accelerator for computer iteration". International Journal of Numerical Methods in Engineering 1, 275-277 (1969).
Pointwise Aitken-acceleration:

//Set a boolean flag that controls whether pointwise Aitken

//extrapolation is used. The optional argument specifies the Picard

//Iteration after which the extrapolation is to be used for the first

//time. The default value is zero.

void enable_pointwise_aitken (const unsigned &pointwise_aitken_start)

If this function is called, the classical Aitken extrapolation is used to accelerate the convergence of (individual) solid degrees of freedom after every three iterations.

The SegregatedFSICollapsibleChannelProblem

We shall now briefly discuss the application of the segregated solver for the collapsible channel problem. The SegregatedFSICollapsibleChannelProblem is defined in the driver code simple_segregated_driver.cc and inherits from the "monolithic" FSICollapsibleChannelProblem and also from the SegregatableFSIProblem class. The code simple_segregated_driver.cc is specifically designed for ease of exposition and does not contain any timing statements or documentation of convergence histories. The alternative driver code fsi_chan_seg_driver.cc contains complete timing and documentation statements and is the code that was used by Heil, Hazel & Boyle (2008).

The simplified SegregatedFSICollapsibleChannelProblem class contains six member functions

The constructor
The destructor
void identify_fluid_and_solid_dofs(...)
void actions_before_newton_convergence_check()
void actions_before_segregated_convergence_check()
void steady_run()
void doc_solution(DocInfo& doc_info)

The doc_solution(...) function simply writes the bulk (fluid) elements and wall (solid) elements to two separate files and the destructor is empty. We discuss the other four member functions below.

The constructor

The constructor calls the constructor of the underlying "monolithic" problem and then selects the convergence criterion and convergence-acceleration technique based on the values of control flags defined in the namespace Flags.

//=====start_of_constructor======================================
/// Constructor for the collapsible channel problem
//===============================================================
template <class ELEMENT>
SegregatedFSICollapsibleChannelProblem< ELEMENT>::
SegregatedFSICollapsibleChannelProblem(const unsigned& nup, 
                                       const unsigned& ncollapsible,
                                       const unsigned& ndown,
                                       const unsigned& ny,
                                       const double& lup,
                                       const double& lcollapsible, 
                                       const double& ldown,
                                       const double& ly,
                                       const bool& displ_control,
                                       const bool& steady_flag) :
 FSICollapsibleChannelProblem<ELEMENT>(nup, 
                                       ncollapsible,
                                       ndown,
                                       ny,
                                       lup,
                                       lcollapsible, 
                                       ldown,
                                       ly,
                                       displ_control,
                                       steady_flag) 
{
 // Choose convergence criterion based on Flag::Convergence criterion
 // with tolerance given by Flag::Convergence_tolerance
 if (Flags::Convergence_criterion==0)
  {
   assess_convergence_based_on_max_global_residual(
    Flags::Convergence_tolerance);
  }
 else if (Flags::Convergence_criterion==1)
  {
   assess_convergence_based_on_absolute_solid_change(
    Flags::Convergence_tolerance);
  }
 else if (Flags::Convergence_criterion==2)
  {
   assess_convergence_based_on_relative_solid_change(
    Flags::Convergence_tolerance);
  }
 
 //Select a convergence-acceleration technique based on control flags
 
 // Pointwise Aitken extrapolation
 if(Flags::Use_pointwise_aitken)
  {
   this->enable_pointwise_aitken();
  }
 else
  {
   this->disable_pointwise_aitken();
  }
 
 // Under-relaxation
 this->enable_under_relaxation(Flags::Omega_under_relax);
 
 // Irons and Tuck's extrapolation
 if(Flags::Use_irons_and_tuck_extrapolation)
  {
   this->enable_irons_and_tuck_extrapolation();
  }
 else
  {
   this->disable_irons_and_tuck_extrapolation();
  }
 
} //end_of_constructor

Identifying the fluid and solid degrees of freedom

The underlying monolithic problem provides pointers to the fluid and solid (sub-)meshes via the member data

AlgebraicCollapsibleChannelMesh<ELEMENT>* Bulk_mesh_pt;

OneDLagrangianMesh<FSIHermiteBeamElement>* Wall_mesh_pt;

which are accessible via the member functions
SegregatedFSICollapsibleChannelProblem::bulk_mesh_pt() and SegregatedFSICollapsibleChannelProblem::wall_mesh_pt(), and so the identification of fluid and solid degrees of freedom is reasonably straightforward. The only complication arises because we may, or may not, be using displacement control which introduces a further element into the global mesh. Displacement control affects the solid problem suggesting that the (variable) external pressure should be regarded as a solid degrees of freedom and the DisplacementControlElement should be included in the solid mesh.

//=====start_of_identify_fluid_and_solid======================================
/// Identify the fluid and solid Data and the meshes that
/// contain only elements that are involved in the respective sub-problems. 
/// This implements a pure virtual function in the 
/// SegregatableFSIProblem base class.
//============================================================================
template <class ELEMENT>
void SegregatedFSICollapsibleChannelProblem<ELEMENT>::
identify_fluid_and_solid_dofs(Vector<Data*>& fluid_data_pt,
                              Vector<Data*>& solid_data_pt,
                              Mesh*& fluid_mesh_pt,
                              Mesh*& solid_mesh_pt)
{
 
 //FLUID DATA: 
 //All fluid elements are stored in the Mesh addressed by bulk_mesh_pt() 
 
 //Reset the storage
 fluid_data_pt.clear();
 
 //Find number of fluid elements
 unsigned n_fluid_elem=this->bulk_mesh_pt()->nelement();
 //Loop over fluid elements and add internal data to fluid_data_ptt
 for(unsigned e=0;e<n_fluid_elem;e++)
  {
   GeneralisedElement* el_pt=this->bulk_mesh_pt()->element_pt(e);
   unsigned n_internal=el_pt->ninternal_data();
   for(unsigned i=0;i<n_internal;i++)
    {
     fluid_data_pt.push_back(el_pt->internal_data_pt(i));
    }
  }
 
 //Find number of nodes in fluid mesh
 unsigned n_fluid_node=this->bulk_mesh_pt()->nnode();
 //Loop over nodes and add the nodal data to fluid_data_pt
 for (unsigned n=0;n<n_fluid_node;n++)
  {
   fluid_data_pt.push_back(this->bulk_mesh_pt()->node_pt(n));
  }
  
 // The bulk_mesh_pt() is a mesh that contains only fluid elements
 fluid_mesh_pt = this->bulk_mesh_pt(); 
 
 
 //SOLID DATA
 //All solid elements are stored in the Mesh addressed by wall_mesh_pt()
 
 //Reset the storage
 solid_data_pt.clear();
 
 //Find number of nodes in the solid mesh
 unsigned n_solid_node=this->wall_mesh_pt()->nnode();
 //Loop over nodes and add nodal position data to solid_data_pt
 for(unsigned n=0;n<n_solid_node;n++)
  {
   solid_data_pt.push_back(
    this->wall_mesh_pt()->node_pt(n)->variable_position_pt());
  }
   
 //If we are using displacement control then the displacement control element
 //and external pressure degree of freedom should be treated as part
 //of the solid problem
 
 //We will assemble a single solid mesh from a vector of pointers to meshes
 Vector<Mesh*> s_mesh_pt(1);
 //The wall_mesh_pt() contains all solid elements and is the first
 //entry in our vector
 s_mesh_pt[0]=this->wall_mesh_pt();
  
 //If we are using displacement control
 if (this->Displ_control)
  {
   //Add the external pressure data to solid_data_pt
   solid_data_pt.push_back(Global_Physical_Variables::P_ext_data_pt);
   //Add a pointer to a Mesh containing the displacement control element
   //to the vector of pointers to meshes
   s_mesh_pt.push_back(this->Displ_control_mesh_pt);
  } 
 
 // Build "combined" mesh from our vector of solid meshes
 solid_mesh_pt = new Mesh(s_mesh_pt);
 
} //end_of_identify_fluid_and_solid

Actions before convergence checks

During a monolithic solve the function actions_before_newton_convergence_check() must update the nodal positions in the bulk (fluid) mesh. In principle, it should remain empty during a segregated solve, but we found it beneficial to update the bulk mesh, and hence the fluid load on the wall, during the solution of the solid problem.

The function actions_before_segregated_convergence_check() contains an update of the nodal positions in the bulk mesh in order that the segregated solution is self-consistent.

 /// Update nodal positions in the fluid mesh in
 /// response to changes in the wall displacement field after every
 /// Newton step in a monolithic or segregated solid solve. Note
 /// the use of the (protected) flag Solve_type, which can take the
 /// values Full_solve, Fluid_solve or Solid_solve. This flag is used
 /// to allow specification of different actions depending on the
 /// precise solve taking place.
 void actions_before_newton_convergence_check()
  {
   //For a "true" segregated solver, we would not do this in fluid or solid
   //solves, but adding the bulk node update to the solid solve phase aids
   //convergence and makes it possible for larger values of Q. Of course,
   //there is a small cost associated with doing this.
   if(Solve_type!=Fluid_solve) {this->Bulk_mesh_pt->node_update();}
  }
 
 
 /// Update nodal positions in the fluid mesh
 /// in response to any changes in the wall displacement field after every 
 /// segregated solve. This is not strictly necessary because we
 /// do the solid solve last, which performs its own node update before the 
 /// convergence check of the sub problem. It remains here because if we
 /// were solving in a completely segregated fashion a node update would be 
 /// required for the fluid mesh in the final converged solution to be
 /// consistent with the solid positions.
 void actions_before_segregated_convergence_check()
  { 
   this->Bulk_mesh_pt->node_update();
  } 
 
 // end_of_convergence_checks

Solving a steady problem

The function steady_run() conducts a simple parameter study in which the external pressure (or prescribed displacement) is varied. After specification of the initial conditions, parameter increments and output directories, the parameter study is straightforward

 // Parameter study (loop over the number of steps)
 for (unsigned istep=0;istep<Flags::Nsteps;istep++)
  {
   // Setup segregated solver 
   //(Default behaviour will identify the fluid and solid dofs and
   // allocate memory, etc every time. This is a bit inefficient in 
   // this case, but it is safe and will always work)
   setup_segregated_solver();
 
   // SEGREGATED SOLVER
   if(Flags::Use_segregated_solver)
    {
     //Set the maximum number of Picard steps
     Max_picard =50;
     
     // Solve ignoring return type (convergence data)
     (void)steady_segregated_solve();
    }
   // NEWTON SOLVER
   else
    {
     //Explit call to the steady Newton solve.
     steady_newton_solve();
    }
   
   // Output the solution
   doc_solution(doc_info);
   
   //Increase the Step number
   doc_info.number()++;
   
   // Adjust control parameters
   //If displacment control increment position
   if (this->Displ_control)
    {
     Global_Physical_Variables::Yprescr+=delta_y;
    }
   //Otherwise increment external pressure
   else
    {
     double old_p=Global_Physical_Variables::P_ext_data_pt->value(0);
     Global_Physical_Variables::P_ext_data_pt->set_value(0,old_p+delta_p);
    }
 
  } // End of parameter study

The driver code

Having written our SegregatedFSICollapsibleChannelProblem, the driver code is extremely simple. We specify number of elements and dimensions of our computational domain, construct the problem and perform a steady parameter study.

//============start_of_main====================================================
/// Driver code for a segregated collapsible channel problem with FSI.
//=============================================================================
int main()
{
 // Number of elements in the domain
 unsigned nup=4*Flags::Resolution_factor;
 unsigned ncollapsible=20*Flags::Resolution_factor;
 unsigned ndown=40*Flags::Resolution_factor;
 unsigned ny=4*Flags::Resolution_factor;
  
 
 // Geometry of the domain
 double lup=1.0;
 double lcollapsible=5.0;
 double ldown=10.0;
 double ly=1.0;
 
 // Steady run by default
 bool steady_flag=true;
 // with displacement control
 bool displ_control=true;
 
 // Build the problem with QTaylorHoodElements
 SegregatedFSICollapsibleChannelProblem
  <AlgebraicElement<QTaylorHoodElement<2> > > 
  problem(nup, ncollapsible, ndown, ny, 
          lup, lcollapsible, ldown, ly, displ_control,
          steady_flag);
 
 //Perform a steady run
 problem.steady_run();
 
}//end of main

Comments and Exercises

Comments

(In-)efficiency of setup_segregated_solver()

In our simple example code, we did not employ spatial adaptivity. It is not necessary, therefore, to (re-)identify the fluid and solid degrees of freedom before each solve, the default (safe) behaviour of setup_segregated_solver(). Nonetheless, data associated with the techniques used to accelerate the convergence of the Picard iterations must be reset before each segregated solve. In the more complex driver code, a boolean flag bool full_setup is used as an argument to setup_segregated_solver() which modifies the behaviour, as indicated below.
// Boolean flag used to specify whether a full setup of solid and fluid dofs

// is required

bool full_setup = true;

// Parameter study

for (unsigned istep=0;istep<Flags::Nsteps;istep++)

{

// Setup segregated solver

setup_segregated_solver(full_setup);

[...]

steady_segregated_solve()

[...]

//We no longer need a full setup of the dofs

full_setup = false;

}

.

Exercises

Modify the control flags in simple_segregated_driver.cc to verify that the monolithic solution is the same (to within finite precision) as the segregated solution.
Modify the control flags in simple_segregated_driver.cc to investigate the influence of the convergence acceleration techniques and convergence criterion on the segregated solution. Which combination of parameters gives convergence in the fewest Picard iterations?
Investigate the behaviour of the system if the fluid (bulk) mesh is not updated after each Newton step in the solution of the solid problem. Can you obtain converged solutions?
Write your own SegregatedFSICollapsibleChannelFlow::unsteady_run() member function that computes the time evolution of the system after a perturbation to the external pressure. Compare your answer with the equivalent member function in the much more comprehensive driver code fsi_chan_seg_driver.cc that was used in Heil, Hazel & Boyle (2008). .

Source files for this tutorial

The source files for this tutorial are located in the directory: demo_drivers/interaction/fsi_channel_seg_and_precond/
The driver code is: demo_drivers/interaction/fsi_channel_seg_and_precond/simple_segregated_driver.cc

PDF file

A pdf version of this document is available.